Fyzikální podstata zvuku – vlnová rovnice
Obr. 1: Příčné a podélné vlnění
Zvuk je mechanické vlnění pružného prostředí, které vnímáme sluchem. Definice zvuku tak má dvě části: fyzikální „mechanické vlnění pružného prostředí“ a fyziologickou „které vnímáme sluchem“. V pevných látkách se může zvuk šířit podélným nebo příčným vlněním anebo jejich kombinací – např. ohybovým nebo torsním vlněním. V plynech a kapalinách však dochází pouze k podélnému vlnění. To je charakteristické tím, že směr kmitání jednotlivých malých částí hmoty je shodný se směrem šíření vlny. Souvislost mezi příčným a podélným vlněním je naznačena na obr. 1. Od místa vzniku vlnění (zdroje zvuku) se vlnění šíří postupně. To je příčinou toho, že sousední částice hmoty kmitají vždy s rozdílnou fází tak, jak vlnění do různých míst s různým časovým zpožděním dospělo. Výsledkem tohoto nestejného pohybu částic jsou místní a časové změny hustoty a tedy i tlaku plynu. Tyto změny popisuje vlnová rovnice.
Barometrický tlak p0 [Pa] se mění jen zvolna v závislosti na atmosférických podmínkách. Rozdíl mezi barometrickým tlakem a skutečným tlakem plynu při akustickém ději se nazývá akustický tlak p [Pa]. Změny akustického tlaku naopak probíhají velmi rychle tak, že v tomto krátkém čase nemůže dojít k významné výměně tepla mezi jednotlivými částicemi plynu. Proto se uvedené změny považují za adiabatické. Platí stavová rovnice plynu
kde pc [Pa] je počáteční celkový tlak, V0 [m3] je počáteční objem plynu odpovídající pouze počátečnímu tlaku. Ten se při působení akustického tlaku změní na (V0 + ΔV). Mocnitel γ [-] je poměr měrných tepelných kapacit plynu
cp [J kg−1 K−1] je měrná tepelná kapacita při konstantním tlaku a cv [J kg−1 K−1] je měrná tepelná kapacita při konstantním objemu. Pro vzduch (bez CO2) je γ = 1,4. Po úpravě rovnice (1) se může psát
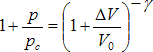 (3)
(3)Protože ![]() je velmi malé, lze rovnici (3) aproximovat na tvar
je velmi malé, lze rovnici (3) aproximovat na tvar
Z rovnice (4) lze vyjádřit akustický tlak
kde K = γ‧pc [Pa] je objemový modul pružnosti plynu.
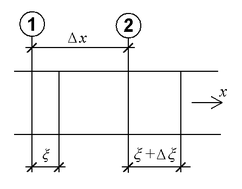
Obr. 2: K odvození vlnové rovnice
Relativně jednoduchým příkladem šíření zvuku jsou rovinné vlny. Časové a prostorové změny akustického tlaku nastávají jen ve směru x šíření zvukových vln, zatímco při změně souřadnic y a z zůstává tlak konstantní. Možným příkladem rovinných vln je šíření zvuku v přímém potrubí o jednotkové průřezové ploše S = 1 m2 (viz vyobrazení). Částice v rovině ![]() mají okamžitou výchylku ξ [m] a částice v rovině
mají okamžitou výchylku ξ [m] a částice v rovině ![]() , která je od roviny
, která je od roviny ![]() vzdálena Δx metrů, mají okamžitou výchylku
vzdálena Δx metrů, mají okamžitou výchylku
Původní objem V0 = Δx vymezený sledovanými rovinami ![]() a
a ![]() vzroste o hodnotu
vzroste o hodnotu
Poměr ![]() lze dosadit do vztahu (5)
lze dosadit do vztahu (5)
Jestliže v rovině ![]() působí akustický tlak p [Pa], pak v rovině
působí akustický tlak p [Pa], pak v rovině ![]() působí tlak
působí tlak
Rozdíl ![]() tlaků způsobí pohyb plynu mezi oběma rovinami. Hmotnost vzduchu mezi oběma rovinami (plošná hmotnost, neboť průřezová plocha myšleného potrubí je 1 m2) je m´ = ρ ‧ Δx [kg.m−2]. Lze použít Newtonovy pohybové zákony F = −m ‧ a, kde sílu lze nahradit tlakem, hmotnost plošnou hmotností a zrychlení vyjádřit jako druhou derivaci výchylky podle času.
tlaků způsobí pohyb plynu mezi oběma rovinami. Hmotnost vzduchu mezi oběma rovinami (plošná hmotnost, neboť průřezová plocha myšleného potrubí je 1 m2) je m´ = ρ ‧ Δx [kg.m−2]. Lze použít Newtonovy pohybové zákony F = −m ‧ a, kde sílu lze nahradit tlakem, hmotnost plošnou hmotností a zrychlení vyjádřit jako druhou derivaci výchylky podle času.
Dělením obou stran rovnice (10) Δx se obdrží pohybová rovnice
která se dále derivuje podle x a upraví.
Rovnici (8) lze derivovat dvakrát podle času
Dosazením pravé strany rovnice (12) za odpovídající část pravé stany rovnice (13) se obdrží vlnová rovnice
kde ![]() [m.s−1] je rychlost zvuku. Při teplotě 0 °C, běžném tlaku p0 = 101,325 kPa a objemové hmotnosti vzduchu ρ0 = 1,29 kg.m-3 je rychlost zvuku ve vzduchu c0 = 331,5 m.s−1. Rychlost zvuku ve vzduchu se nepatrně mění s teplotou. Pro technické výpočty se používá hodnota c0 = 340 m.s−1 odpovídající teplotě 14,2 °C.
[m.s−1] je rychlost zvuku. Při teplotě 0 °C, běžném tlaku p0 = 101,325 kPa a objemové hmotnosti vzduchu ρ0 = 1,29 kg.m-3 je rychlost zvuku ve vzduchu c0 = 331,5 m.s−1. Rychlost zvuku ve vzduchu se nepatrně mění s teplotou. Pro technické výpočty se používá hodnota c0 = 340 m.s−1 odpovídající teplotě 14,2 °C.
Eliminací p lze z rovnic (8) a (11) získat vlnovou rovnici pro výchylku
V pravoúhlých souřadnicích x, y, z pro třírozměrný prostor má vlnová rovnice tvar
Jako řešení vlnové rovnice vyhovuje každá funkce g s argumentem (t − x / c), což lze dokázat dosazením druhých parciálních derivací
do rovnice (14). Specielně pro harmonické (sinové nebo kosinové) vlnění lze jako řešení vlnové rovnice (14) uvažovat funkci
kde A [Pa] je amplituda akustického tlaku a ω [s−1] je kruhová frekvence. Ta je rovna 2π násobku kmitočtu f [Hz]. Kmitočet vyjadřuje rychlost opakování kmitavého pohybu počtem kmitů za sekundu.
Obdobně pro harmonické vlnění je řešením rovnice (15) funkce
kde U [m] je amplituda výchylky.
V rovnicích (18) a (20) je ![]() [m−1] vlnové číslo a λ [m] je vlnová délka tj. dráha, kterou urazí vlna během jednoho kmitu. Vlnová délka souvisí s kmitočtem
[m−1] vlnové číslo a λ [m] je vlnová délka tj. dráha, kterou urazí vlna během jednoho kmitu. Vlnová délka souvisí s kmitočtem
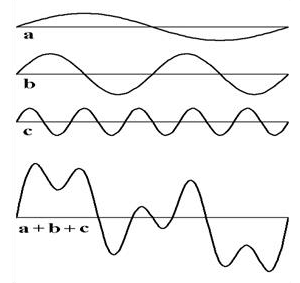
Obr. 3: Součet tří harmonických vlnění
Pro analýzu zvuku má harmonické vlnění zvláštní význam. Složitější periodické pohyby částic lze totiž vždy vyjádřit jako součet konečného počtu nebo definované nekonečné řady harmonických pohybů s různými amplitudami a úhlovými rychlostmi (a tedy i různými kmitočty a vlnovými délkami). Jako příklad je vyobrazeno příčné vlnění, které vznikne jako součet tří vlnění harmonických. Je však třeba mít na paměti, že v akustice se jedná o vlnění podélné. Ale i to je vždy možné rozkládat na jednotlivá vlnění harmonická. Rozklad funkce na její harmonické složky je spojen se jménem francouzského matematika a fyzika Jean-Baptiste Joseph Fouriera (1768–1830). Technická akustika však podrobnou analýzu kmitočtů nahrazuje jednodušší představou akustického spektra. Akustickým spektrem se rozumí soustava hodnot sledované akustické veličiny (např. hladiny akustického tlaku) uváděná v závislosti na kmitočtu. Často se uvádí formou grafu nebo tabulky. Při výpočtech se často používá oktávové spektrum v rozsahu 125 až 4000 Hz, případně doplněné o oktávy 63 a 8000 Hz. Zvuk o kmitočtu nižším než 125 resp. 63 Hz je vnímán sluchem člověka s malou citlivostí a nebývá proto zpravidla příčinou závad. Zvuk o vyšším kmitočtu než 4000 resp. 8000 Hz je při šíření v budovách dobře tlumen, takže se na závadách zpravidla také nepodílí.