Neprůzvučnost homogenních a izotropních jednoduchých stavebních prvků

Neprůzvučnost jednoduchých stavebních prvků je ovlivněna jak vlastnostmi zvukového pole, které na prvek působí ze strany místnosti zdroje, tak materiálovými a konstrukčními parametry stavebního prvku. Z pohledu praxe je nejdůležitější neprůzvučnost pro difúzní dopad zvukové vlny, resp. pro praktické rozmezí úhlu dopadu přibližně od 0° do 78°. Teoretický průběh neprůzvučnosti homogenního a izotropního jednoduchého stavebního prvku pro takový dopad zvuku v závislosti na kmitočtu je na obrázku 4.

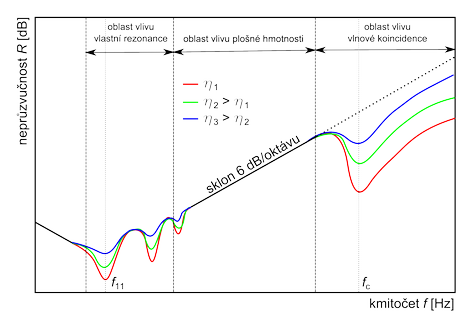
Obr. 4 – Teoretický průběh neprůzvučnosti jednoduchého stavebního prvku v závislosti na kmitočtu

Pro neprůzvučnost jednoduchých stavebních prvků jsou nejdůležitější tři kmitočtové oblasti:

1. oblast vlivu vlastní rezonance,
2. oblast vlivu plošné hmotnosti,
3. oblast vlivu vlnové koincidence.

V oblasti vlivu vlastní rezonance je neprůzvučnost ovlivněna řadou výrazných lokálních poklesů. Tyto poklesy odpovídají polohám jednotlivých vlastních rezonančních kmitočtů deskového prvku. Neprůzvučnost je v této oblasti obtížně předpověditelná a podstatně závisí na rozměrech a ohybové tuhosti stavebního prvku. Hloubka jednotlivých poklesů je dána tlumením prvku (hodnotami ztrátového činitele η).

V oblasti vlivu plošné hmotnosti je efektivně využita plošná hmotnost prvku. Neprůzvučnost zde roste o 6 dB na oktávu. Průběh neprůzvučnosti bývá hladký, neprůzvučnost dosahuje svého teoretického maxima.

V oblasti vlivu vlnové koincidence dochází k výraznému poklesu neprůzvučnosti v důsledku koincidence mezi vynucenou ohybovou vlnou a volnou ohybovou vlnou v konstrukci. Hloubka poklesu je dána opět tlumením prvku, tj. hodnotami ztrátového činitele. Pro většinu těžkých jednoduchých stavebních prvků je oblast vlivu vlnové koincidence převládající oblastí prakticky v celém zvukově izolačním pásmu.

Oblast vlivu plošné hmotnosti prvku/Mass Controlled Region

Neprůzvučnost jednoduchých prvků závisí na poměru vlnové impedance materiálu Z_m a vlnové impedance okolního prostředí (vzduchu) Z₀. Zvukově izolační konstrukce se vyznačují poměrem Z_m / Z₀ >> 1. Pro vlnovou impedanci materiálu platí vztah:

Z_m = ρ_m ‧ c_L[Pa.s.m⁻¹](8)

kde ρ_m je objemová hmotnost a c_L je rychlost podélných zvukových vln v materiálu. Obdobně platí Z₀ = ρ₀ ‧ c₀. Neprůzvučnost tenkého stavebního prvku pro kolmý dopad zvukové vlny je dána vztahem:

[dB](9)

kde k_m je vlnové číslo a m´ je plošná hmotnost prvku v kg.m⁻² (m´ = ρ_m ‧ t). Tento vztah se nazývá zákon hmotnosti a definuje neprůzvučnost v oblasti vlivu plošné hmotnosti, kde roste s kmitočtem o 6 dB/oktávu. Rovněž o 6 dB neprůzvučnost teoreticky vzroste při zdvojnásobení plošné hmotnosti. V budovách, kde zvuk dopadá na konstrukci pod různými úhly (přibližně od 0° do 78°), je neprůzvučnost o něco nižší:

R ≅ R₀ − 5 = 20 ‧ lg (m´f) − 47,5[dB].(10)

V oblasti vlivu plošné hmotnosti dosahuje neprůzvučnost prvku svého maxima a proto je výhodné, aby tato kmitočtová oblast pokrývala co největší část zvukově izolačního pásma.

Oblast vlivu vlnové koincidence/Coincidence Region

Zvuková vlna dopadající na prvek (s výjimkou kolmého dopadu) vyvolá v prvku ohybové vlnění. Délka ohybové vlny λ_B je dána průmětem (kolmým na směr šíření zvukové vlny) vlnové délky zvuku ve vzduchu λ₀ do roviny prvku:

λ_B = λ₀sinθ[m](11)

kde θ je úhel dopadu. Platí tedy, že:

c_B = c₀sinθ[m.s⁻¹](12)

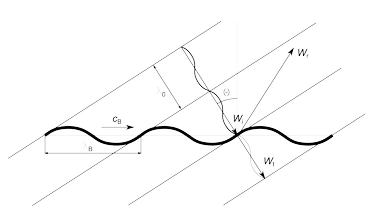
Obr. 5 – Vznik vynuceného ohybového vlnění při dopadu zvuku na konstrukci

kde c_B je rychlost šíření ohybových vln v konstrukci a c₀ je rychlost zvuku ve vzduchu (≈ 343 m.s⁻¹). Pro tento druh přenosu, který se nazývá vynucený, závisí rychlost ohybových vln v prvku na úhlu dopadu zvukové vlny a je vždy větší nebo rovna rychlosti zvuku ve vzduchu. Jestliže pro určitý úhel dopadu nastane situace, že rychlost vynucených ohybových vln je rovna rychlosti volných ohybových vln, potom dochází k jevu nazývanému vlnová koincidence. Ta se projevuje těsnou vazbou mezi prostředím a konstrukcí a tedy i zvýšeným přenosem zvuku a poklesem neprůzvučnosti konstrukce v porovnání s oblastí vlivu plošné hmotnosti.

Pro rychlost volných ohybových vln v desce platí následující vztah:

[m.s⁻¹](13)

kde B je ohybová tuhost a m´ je plošná hmotnost prvku. Po dosazení do předešlého vztahu tak můžeme získat hodnotu koincidenčního kmitočtu f_c,θ při daném úhlu dopadu θ:

[Hz].(14)

Z praktického hlediska je nejdůležitější nejnižší kmitočet vlnové koincidence, tzv. kritický kmitočet, který zdola ohraničuje oblast vlivu vlnové koincidence. Kritický kmitočet se získá pro tečný dopad zvuku na stavební prvek úpravou předchozího vztahu:

[Hz].(15)

Druhá část vztahu je vhodnou aproximací pro homogenní deskové prvky obdélníkového průřezu. Protože hodnoty c₀ a c_L jsou konstanty, kritický kmitočet jednoduchého stavebního prvku je funkcí jeho tloušťky t.

Pro většinu běžných příček se kritický kmitočet nachází uvnitř zvukově izolačního pásma (tj. mezi 1/3 oktávovými pásmy 100 Hz a 3150 Hz). Jeho vytěsnění mimo tuto oblast je někdy možné zajistit změnou ohybové tuhosti příčky. U tenkých deskových prvků, které jsou charakteristické výrazným poklesem neprůzvučnosti v okolí kritického kmitočtu, toho lze efektivně dosáhnout kombinací více deskových prvků menší tloušťky – např. tří sádrokartonových desek tl. 10 mm namísto dvou desek tl. 15 mm. Desky však nesmí být vzájemně celoplošně tuze spojené (například lepením).

Oblast vlivu vlastní rezonance/Resonance Region

Když vynucená ohybová vlna dorazí k okraji prvku (styku s ostatními stavebními prvky), částečně se odrazí zpět a z části je pohlcena. Odražená ohybová vlna se šíří rychlostí volných ohybových vln a při každém dopadu na okraj prvku se část vlny znovu odráží zpět. Nastane-li situace, že kmitočet vlnění je shodný s některým z vlastních kmitočtů prvku, dochází k vlastní rezonanci a s ní spojenému zvýšenému přenosu zvuku. Tento druh přenosu se nazývá rezonanční. Pro homogenní, prostě uložené deskové prvky jsou vlastní kmitočty určeny vztahem:

[Hz](16)

kde l_x a l_y jsou rozměry prvku (délka a šířka) a m a n jsou čísla módů (kladná celá čísla). Módy kmitání jsou charakteristické obrazce vytvářené volným kmitáním prvku – na následujícím odkazu jsou znázorněny módy (1,1), (1,2), (2,1) a (2,2): Vibrational Modeshapes of a Rectangular Membrane - Dan Russell.

Nejnižší vlastní kmitočet f₁₁ se nazývá základní kmitočet. Tento kmitočet zdola ohraničuje oblast vlivu vlastní rezonance. Ve stavební akustice, kde se neprůzvučnost stanovuje v kmitočtových pásmech (oktávových nebo třetinooktávových), je důležitým údajem o rozložení vlastních kmitočtů průměrný počet módů uvnitř daného kmitočtového pásma. Ten je pro třetinooktávová pásma dán vztahem:

ΔN ≅  0,23 ‧ πc₀²l_x l_y f_c f [-].(17)

Je zřejmé, že s narůstajícím středním kmitočtem roste také průměrný počet módů uvnitř třetinooktávových pásem a tedy i význam rezonančního přenosu. Zatímco pod kritickým kmitočtem je neprůzvučnost určena především vynuceným přenosem, nad kritickým kmitočtem dominuje rezonanční přenos.

Vliv zabudování prvku do stavby/Influence of Mounting Conditions

Při měření neprůzvučnosti v laboratoři je prvek standardně zabudován do těžkého zkušebního železobetonového rámu, na stavbě je však po obvodě spojen s ostatními stavebními prvky. Tento rozdílný způsob zabudování ovlivňuje pohltivost ohybových vln na okrajích prvku. Podle ČSN EN 12354-1 se činitel zvukové pohltivosti pro ohybové vlny α_k v budovách s těžkými stavebními prvky pohybuje v rozmezí 0,05 až 0,5, v laboratoři podle EN ISO 140-3 má hodnotu kolem 0,15. S narůstající hodnotou činitele pohltivosti se zkracuje doba doznívání stavebního prvku T_s a roste neprůzvučnost, zejména pro rezonanční přenos. Doba doznívání prvku je dána následujícím vztahem:

T_s =  2,2f η_tot [s](18)

kde η_tot je celkový ztrátový činitel, který se skládá ze tří složek:

[-](19)

kde η_int je vnitřní ztrátový činitel materiálu (související s přeměnou akustického výkonu v tepelný, pro běžné homogenní stavební materiály nabývá hodnoty přibližně 0,01), η_rad je ztrátový činitel zohledňující ztráty vyzařováním zvuku do vzduchu (obvykle je možné ho zanedbat) a poslední člen vyjadřuje ztráty pohltivostí na okrajích prvku (zde S je plocha prvku a l_k je délka styku na okraji k).

Pro přepočet laboratorní neprůzvučnosti R_lab na hodnotu in-situ R_situ, v závislosti na skutečné době doznívání prvku T_s,situ, lze použít jednoduchý vztah:

R_situ = R_lab − 10 ‧ lg T_s,situT_s,lab [dB].(20)

Doba doznívání v laboratoři a in-situ je přibližně stejná pro stavební prvky, které jsou výrazně lehčí než okolní stavební prvky nebo s nimi nejsou pevně spojené.

Metody pro výpočet neprůzvučnosti homogenních a izotropních jednoduchých prvků/Prediction Methods for Sound Reduction Index of Single Homogeneous and Izothropic Building Elements

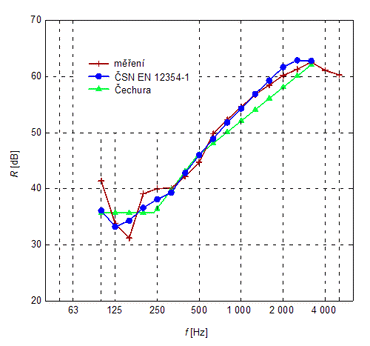
Obr. 6 – Neprůzvučnost zděné příčky z plných cihel tl. 140 mm s oboustrannou omítkou, ve výpočtech byl uvažován celkový ztrátový činitel η_tot pro laboratorní situaci podle ČSN EN 12354-1, ve všech případech R_w = 50 dB

Metody pro odhad neprůzvučnosti jednoduchých stavebních prvků se vyvíjejí převážně od druhé poloviny 20. století. S prohlubujícím se poznáním teorie přenosu zvuku umožňují zahrnout do výpočtu stále více konstrukčních parametrů a stávají se použitelnější i pro moderní stavební konstrukce. Přesto se stále často používají zjednodušené postupy, které takové možnosti neposkytují. Mezi ně patří metody indexové a početně grafické. Indexové metody jsou zaměřené na přímý odhad vážené neprůzvučnosti R_w (dříve indexu neprůzvučnosti), měly by proto sloužit jen pro návrh konstrukce, nikoliv pro její předběžné posouzení. K tomu lze využít početně grafických metod, které umožňují stanovit průběh neprůzvučnosti v závislosti na kmitočtu a jejichž použití je přitom jednoduché a rychlé. Mezi takové metody patří modifikovaná Wattersova metoda, která je založená na práci B. G. Watterse (1959) s modifikacemi podle Čechury (1999), nebo metoda B. H. Sharpa (1978). Vzhledem ke zjednodušujícímu charakteru však i tyto metody mají svá omezení a nelze je použít k odhadu neprůzvučnosti složitějších stavebních konstrukcí. Zde mohou nalézt své uplatnění metody, které jsou sice náročnější na použití, avšak umožňují vypočítat neprůzvučnost „přesně“. Takové výpočtové postupy uvádí zejména zahraniční odborná literatura a jsou zahrnuty i do ČSN EN 12354-1 (2001), příloha B:

f < f_c [dB](21)

f ≥ f_c [dB](22)

kde σ_f je činitel vyzařování pro vynucené ohybové vlny a σ_r je činitel vyzařování pro volné ohybové vlny. Činitelé vyzařování vyjadřují efektivitu, s jakou je akustický výkon vyzařován z chvějících se povrchů. Pomůcka pro výpočet neprůzvučnosti podle ČSN EN 12354-1 (2001) je k dispozici zde. Podrobný popis Wattersovy metody upravené podle J. Čechury lze nalézt například v učebních skriptech: Kaňka J., Stavební fyzika 1 – Akustika budov, ČVUT, 2007.