Program FOKNO v příkladech
Útlum zvuku při ohybu přes překážku je možno stanovit pomocí teorie ohybu vlnění, kterou před dvěma sty lety navrhl francouzský fyzik Augustin-Jean Fresnel. Autor článku s použitím této teorie sestavil program FOKNO. Článek umožňuje jeho volné stažení a obsahuje několik praktických příkladů řešených tímto programem.
Letos si můžeme připomenout 200 let od napsání díla „Mémoire sur la diffraction de la lumière (1818)“, kterým Augustin-Jean Fresnel významně přispěl k formulování teorie vlnové optiky. Přestože Fresnel studoval vlnové jevy na světle, zákonitosti, které stanovil, platí i v akustice, neboť zvuk má také povahu vlnění. Díky skutečnosti, že délka zvukových vln je řádově větší v porovnání s vlnovou délkou světla, se v akustice vlnové jevy v praktickém světě projevují zřetelněji. To platí zejména pro ohyb vlnění. Zvuk se snáze než světlo ohýbá a je přítomen i za překážkou v šíření vln (za clonou) v míře dostatečné k tomu, aby byl vnímán. Úzká vazba vlnových jevů na délku vlny resp. na kmitočet zatím brání významnějšímu využití teorie ohybu v akustice. Většina rušivých zvuků má totiž spojité spektrum. Využití teorie ohybu pro předpověď šíření takového zvuku proto předpokládá analýzu akustického výkonu zdroje ve velmi úzkých pásmech. Snáze lze vlnovou teorii ohybu aplikovat na tónové zvuky. K tomu potřebné základy teorie difrakce lze mimo jiné sledovat v [1] a ve [2]. Na základě vztahů uvedených v těchto příspěvcích byl vyvinut program FOKNO, který je možno zdarma získat zde: fokno.xls. Tento příspěvek je věnován několika praktickým příkladům řešeným tímto programem.
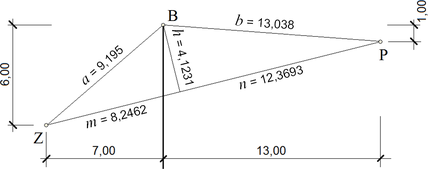
Příklad 1: Protihluková clona 1
Má se stanovit útlum zvuku o kmitočtu 250 Hz velmi dlouhou clonou podle obrázku. Z = zdroj zvuku, B = vrchol (koruna) clony, P = příjemce zvuku.
Řešení
Vlnová délka zvuku λ = c / f = 340 / 250 = 1,36 m.
Výpočet proměnné v (–)
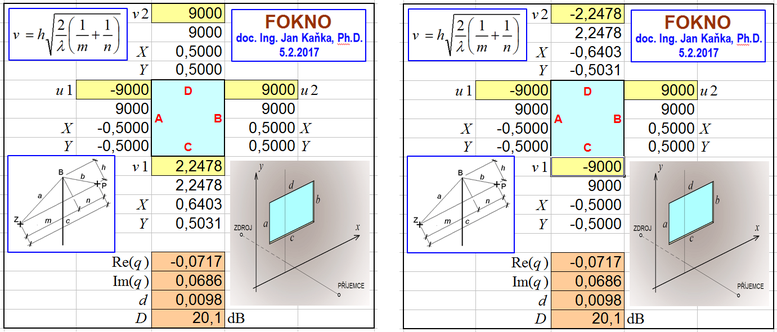
Hodnotu proměnné v (–) zadáme do programu. Program FOKNO pracuje v systému Excel. Zobrazuje pomyslné „okno“, kterým se šíří zvuk. Okno je ohraničeno parapetem (dole), nadpražím (nahoře) a pravým a levým ostěním. Proměnné v (–) ve svislém směru a u (–) ve směru vodorovném se zadávají do žlutě podbarvených polí. Výsledky lze sledovat v polích podbarvených hnědou barvou. Při šíření přes jednoduchou protihlukovou clonu je zvuk omezen pouze zdola – tedy parapetem. Směrem vzhůru omezen není a proto příslušná proměnná v2 = ∞. Zadává se ale v2 = 9000, protože program vyšší hodnoty nezpracuje. Stěna se táhne do nekonečna na pravou i levou stranu. Proto příslušné proměnné mají rovněž hodnotu nekonečno: u1 = −9000 a u2 = +9000. Proměnná pro parapet je podle výsledku výpočtu v1 = 2,2478. Zadání lze sledovat na levé straně obrázku. Na jeho pravé straně je stejný příklad zadaný neuvěřitelně „vzhůru nohama“ – stěna je nahoře a volný prostor dole. Vypočtený útlum je D = 20,1 dB.
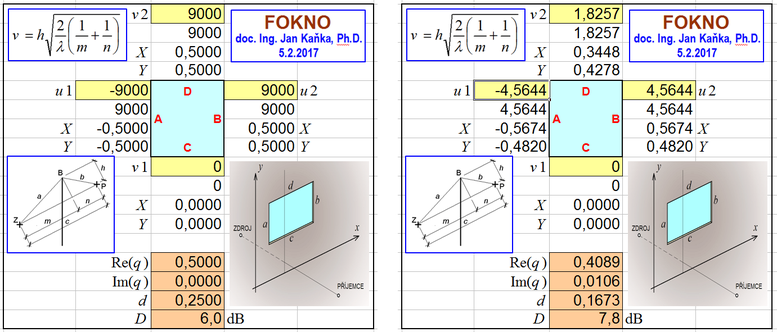
Příklad 2: Protihluková clona 2
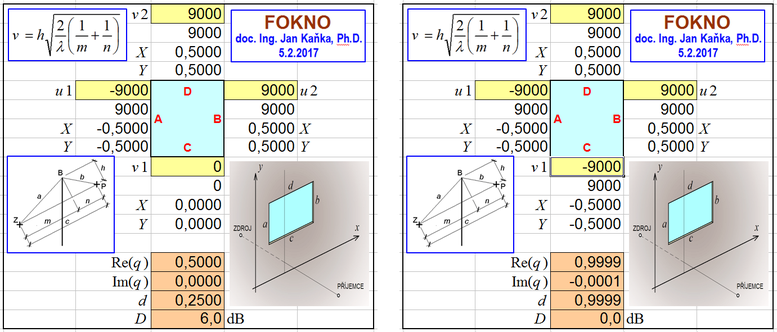
Má se stanovit útlum zvuku clonou pro případ, kdy zdroj Z zvuku, vrchol B clony i příjemce P zvuku leží na jedné přímce. Při takovémto uspořádání je efektivní výška clony h = 0, a proto i proměnná v1 = 0. Zadání je na levé straně obrázku, zatímco na pravé straně obrázku je zadání k příkladu 3. Vypočtený útlum D = 6 dB nezávisí na kmitočtu zvuku.
Příklad 3: Bez protihlukové clony
Jestliže není přítomna protihluková clona, zvuk se šíří volně v celém prostoru. Není omezován v žádném směru, a proto všechny proměnné nabývají hodnoty nekonečno. Při zadání do programu FOKNO hodnoty ±9000. Zadání je v pravé části předchozího obrázku a vypočtený útlum D = 0 dB. Kde neexistuje clona, není ani útlum.
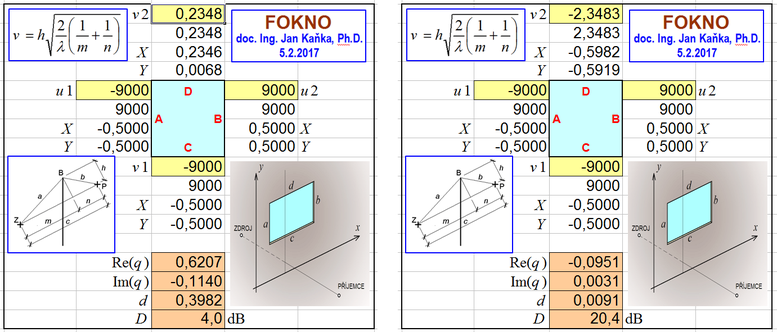
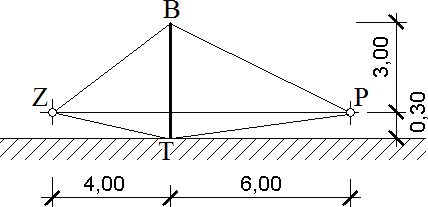
Příklad 4: Stěna postavená na terénu
Má se stanovit útlum zvuku o kmitočtu 250 Hz velmi dlouhou clonou podle obrázku. Stěna je postavená na terénu s povrchem zcela pohlcujícím zvuk. Z = zdroj zvuku, B = vrchol clony, T = pata stěny, P = příjemce zvuku. To, že stěna byla postavena na terénu, není nic neobvyklého, ale vyžaduje to nový přístup k výpočtu. Samotná přítomnost terénu totiž byla příčinou útlumu D1 (dB) už před postavením clony. Po její realizaci vzrostl útlum na hodnotu D2 (dB). Příspěvek clony je nutno stanovit jako rozdíl D = D2 − D1.
Řešení
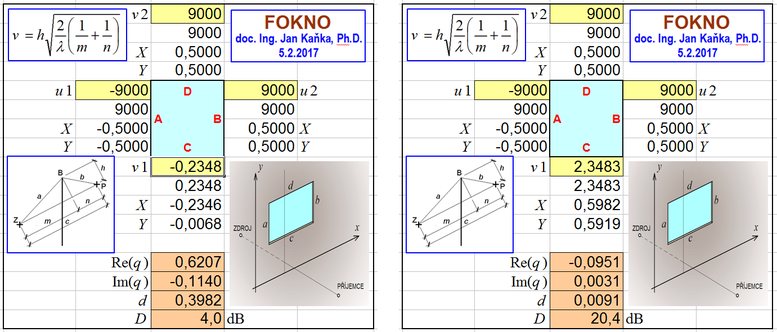
Nejdříve je proveden výpočet pro situaci bez clony, kdy volnému šíření zvuku brání jen přítomnost terénu. Proměnná v1 (–) má zápornou hodnotu. Lze se řídit jednoduchým pravidlem, že zápornou hodnotu přiřadíme proměnným v1 a u1 tehdy, jestliže místo P není clonou od zdroje Z odděleno (z místa P je místo Z „vidět“). A to je právě náš případ, neboť zdroj i pozorovatel zvuku jsou nad terénem. Je ale nutno poznamenat, že proměnným v2 a u2 bychom v takovém případě přiřadili naopak hodnotu kladnou.
Dosazení této hodnoty do programu FOKNO je v levé části obrázku.
Pro situaci obsahující clonu bude již mít příslušná proměnná hodnotu kladnou, protože body Z a P navzájem na sebe přes stěnu „nevidí“.
Dosazení této hodnoty je v pravé části obrázku.
Vložný útlum clony je D = D2 − D1 = 20,4 − 4,0 = 16,4 dB. Na dalším obrázku je stejný příklad zadaný „vzhůru nohama“ obdobně, jako byl variantně řešen příklad číslo 1. Řešení příkladu s terénem, který odráží zvuk, by bylo složitější. Muselo by totiž počítat s interferencí zvukových vln přímých a vln odražených od terénu.
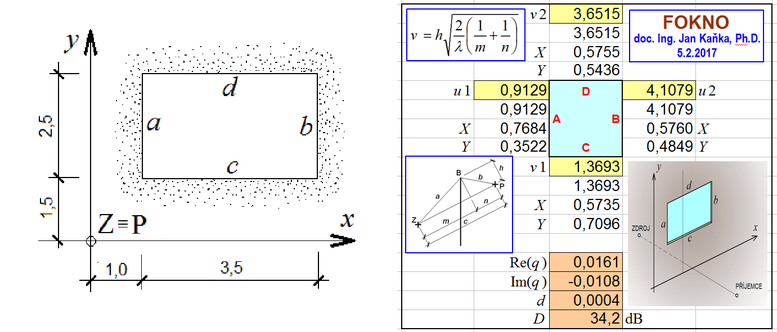
Příklad 5: Obdélník
V tomto příkladu se bude řešit ohyb zvuku při průchodu obdélníkovým otvorem („oknem“ podle obrázku), umístěném ve cloně, která je nekonečná do všech čtyř stran. Vzdálenost zdroje Z zvuku od stěny je m = 2,5 m a vzdálenost místa pozorování P od stěny je n = 6,0 m. S terénem není uvažováno.
Řešení
Postupně se stanoví proměnné při ohybu zvuku přes všechny čtyři hrany, které tvoří zadané „okno“.
Zadání těchto hodnot do programu FOKNO je v pravé části výše uvedeného obrázku. Vypočtený útlum je D = 34,2 dB.
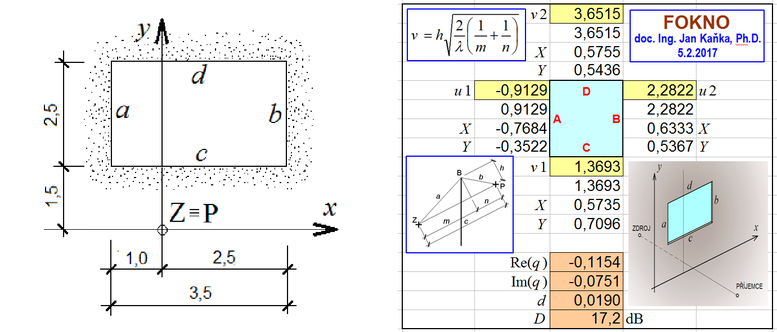
Příklad 6: Posunutý obdélník
V tomto příkladu se bude řešit ohyb zvuku při průchodu obdélníkovým otvorem o stejných rozměrech, jako v předchozím příkladě. Otvor je ale posunut o 2 metry směrem do leva – viz obrázek. Stejně jako v předchozím příkladě jsou vzdálenosti zdroje Z zvuku od stěny m = 2,5 m a místa pozorování P od stěny n = 6,0 m. Také s terénem opět není uvažováno.
Řešení
Postupně se stanoví proměnné při ohybu zvuku přes všechny čtyři hrany, které tvoří zadané „okno“.
Zadání těchto hodnot do programu FOKNO je v pravé části výše uvedeného obrázku. Vypočtený útlum je D = 17,2 dB.
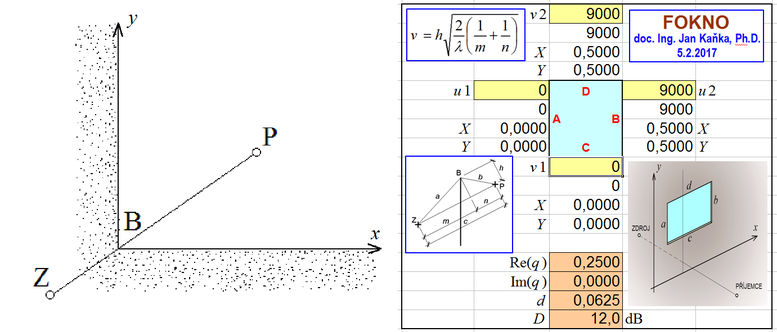
Příklad 7: Čtvrtina prostoru
Podobně jako v příkladu 2 jsou místo P příjemce zvuku, místo Z jeho zdroje a vrchol clony B v jedné přímce. V místě B se ale stýkají dvě kolmo navazující clony, takže zvuk se může šířit jen do čtvrtiny prostoru – prvním kvadrantem pomyslného pravoúhlého x, y prostoru. V takovémto případě u1 = v1 = 0 a u2 = v2 = ∞. Vypočtený útlum D = 12,0 dB. Řešení lze sledovat na následujícím obrázku.
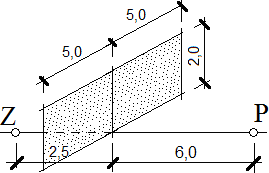
Příklad 8: Clona konečných rozměrů
Zdroj i příjemce zvuku se nacházejí na terénu ve vzdálenosti 8,5 m od sebe. Ve vzdálenosti 2,5 m od zdroje se nachází clona výšky 2,0 m zakončená po stranách ve vzdálenosti 5,0 m od spojnice mezi zdrojem a příjemcem. Je třeba stanovit útlum touto clonou pro zvuk o kmitočtu 250 Hz.
Řešení
Stanoví se proměnná v1 (–) pro šíření zvuku přes vrchol (korunu) clony.
a také proměnné u1 a u2 (–) pro šíření zvuku přes boky clony
Útlum zvuku řešenou clonou se stanoví jako rozdíl útlumu D2 (dB) při stavu s realizovanou clonou mínus útlum D1 (dB) stavu bez clony.
Útlum D1 (dB) se stanoví stejně jako útlum v příkladu 2, protože zdroj Z, pata T budoucí stěny a příjemce P zvuku jsou v jedné přímce.
Po realizaci clony se zvuk bude šířit prostorem X, který je schématicky vyznačen modře v levé části obrázku. Jedná se o šíření poloprostorem A, kterému jsme odebrali část B, jejíž velikost je dána rozměry clony. Prostor X je tak možno sestavit jako poloprostor A, od kterého se odečte prostor „okna“ B. Výpočet poloprostoru A je v levé části obrázku a výpočet „okna“ B je v jeho pravé části.
Při výpočtu složitějších tvarů clon se stanoví činitel útlumu d (–) jako součet druhé mocniny součtu reálných a druhé mocniny součtu imaginárních složek relativního akustického tlaku q (–). Hodnoty Re(q) a Im(q) program FOKNO také poskytuje. Výpočet se provede takto:
Znaménka minus uvnitř závorek jsou v předchozím vztahu proto, že „okno“ se od poloprostoru odečítá. Stanoví se útlum D2 (dB).
Vložný útlum stěny je rozdílem útlumů po realizaci a před realizací clony.
Překvapí nás, že vypočtený útlum je vyšší v porovnání s útlumem stejně vysoké stěny s neomezenou šířkou. Ale je to správně. Kouzlo interference spočívá v oscilacích.
Závěr
Program FOKNO je jistě zajímavá věc na hraní. Autor příspěvku ale věří, že pomocí teorie ohybu vlnění je možno s použitím Fresnelových integrálů již dnes řešit i některé vybrané praktické úkoly. Se zvyšováním možností měřicí a výpočetní techniky zejména směrem k rychlému provádění a zpracování úzkopásmových analýz se rychle blíží doba, kdy teorie ohybu vln najde širší uplatnění v akustické praxi.
Zdroje
- Kaňka, J.: O výpočtech útlumu zvuku ohybem, TZB-info 5. 7. 2010
- Kaňka, J.: Útlum zvuku stěnou konečné délky, TZB-info 20. 2. 2017
The attenuation of bending noise can be determined by the theory of bending waves, which was proposed two hundred years ago by the French physicist Augustin-Jean Fresnel. The author of the paper, using this theory, has compiled the program FOKNO. The article allows its free download and contains several practical examples solved by this program.