O výpočtech útlumu zvuku ohybem
Útlumu zvuku ohybem vlnění se využívá při návrhu protihlukových stěn, clon, bariér a valů podél komunikací s intenzivní pozemní dopravou (silniční, tramvajovou i železniční). Do míst za překážkou v cestě šíření zvuku se zvukové vlny šíří ohybem. Při ohybu dochází ke snížení intenzity zvuku oproti stavu, kdy by v cestě šíření překážka nebyla.
Výpočet ohybu zvuku se využívá při návrhu protihlukových stěn, clon, bariér a valů podél komunikací s intenzivní pozemní dopravou (silniční, tramvajovou i železniční). Ochrana clonami před hlukem stacionárních zdrojů je méně častá, protože je vždy účinnější hlučné zařízení umístit do místnosti uvnitř objektu. Ta je pak větrána vzduchotechnikou přes dostatečně dimenzované absorpční tlumiče zvuku, kterými se utlumí zvuk zdroje i hluk vzduchotechniky. Některá zařízení (například kondenzační jednotky chlazení) však z technologických důvodů do uzavřené místnosti umístit nelze. Spolu s útlumem zvuku se vzdáleností jsou v takových případech protihlukové clony jediným možným způsobem ochrany. Clony lze použít i v uzavřených prostorech (např. výrobních hal). Jejich účinek je ale snižován v důsledku odrazu zvuku od stropu a stěn. Proto je potřebné instalaci clon v interiéru doplnit zvuk pohlcujícím obložením ploch ohraničujících uzavřený prostor.
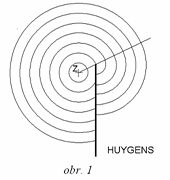
Za každou překážkou na cestě šíření zvuku, jejíž rozměry převyšují vlnovou délku, se vytváří zvukový stín, ve kterém lze pozorovat snížení intenzity zvuku oproti stavu volného šíření zvukových vln bez překážky. Útlum intenzity zvuku závisí na poloze zdroje zvuku, na poloze a geometrickém tvaru překážky, na poloze pozorovatele za překážkou a na vlnové délce zvuku. Vznik a vlastnosti zvukového stínu lze vysvětlit pomocí ohybu vlnění. Zákonitosti ohybu platí pro každé vlnění, tedy i pro vlnění elektromagnetické včetně světla. A právě pro světlo byly tyto zákonitosti nejdříve popsány. Princip šíření vlnění formuloval holandský astronom, fyzik a matematik Christian Huygens (1629 - 1695): Každý bod vlnoplochy je elementárním zdrojem vlnění. Výsledná vlnoplocha má tvar obálky dílčích vlnoploch. Tímto principem se vysvětluje pouze tvar vlnoploch za překážkou (viz obr. 1), nikoli však intenzita.
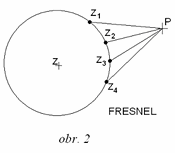
Augustin Jean Fresnel (l788-1827) - byl francouzský fyzik. Zdůvodnil vlnovou teorii světla a mimo jiné na základě Huygensova principu a vlnové interference vysvětlil jeho ohyb. Příslušné zákonitosti platí i pro zvuk. V oblasti praktických aplikací jeho objevů je známá Fresnelova čočka stupňovitě tvořená soustavou soustředných zobrazovacích prvků. Fresnel doplnil Huygensův princip v tomto smyslu: Při sledování intenzity je nutno přihlédnout k interferenci (skládání vlnění). K intenzitě vlnění v bodě P (viz obr. 2) přispívá každý z elementárních zdrojů vlnění - bodů vlnoplochy. Jednotlivé body vlnoplochy jsou však od bodu P různě vzdáleny. Je-li tato vzdálenost sudým násobkem půlvlny, přispěje takový elementární zdroj ke zvýšení intenzity v bodě P. Naopak při vzdálenosti rovné lichým násobkům půlvlny bude vlnění přicházející z příslušného elementárního zdroje v opačné fázi a bude intenzitu snižovat.
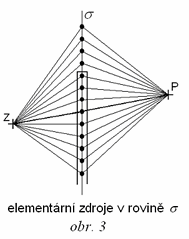
Úvahu je možno zobecnit tím, že namísto souboru elementárních zdrojů na kulové vlnoploše lze uvažovat soubor elementárních zdrojů na jakékoli ploše ležící mezi zdrojem Z a místem příjmu P. Podmínkou je jen to, aby zvolenou plochou procházely všechny možné cesty šíření vln ze zdroje Z do bodu P. S výhodou se za plochu elementárních zdrojů volí rovina σ budoucí stínící překážky. Od bodového zdroje Z se zvukové vlny šíří všemi směry a postupně zasáhnou všechny body roviny σ. Každý bod této roviny kmitá s jinou fází tak, jak k němu vlnění s různým časovým zpožděním dospělo. Všechny tyto body jsou zároveň elementárním zdrojem vlnění pro příjemce P zvuku. Celý soubor elementárních zdrojů zvuku v rovině σ musí mít v místě příjmu stejný účinek, jako původní zdroj. Přes různé body roviny σ přichází vlnění do místa příjmu po odlišné dráze a tedy s odlišným fázovým zpožděním. Vlnění přicházející z místa původního zdroje přímou cestou se skládá s vlněním z jiných směrů, přičemž příspěvky od různých elementárních zdrojů v rovině σ přicházejí do místa příjmu v různé míře se shodnou fází nebo ve fázi opačné a způsobují tak buď zesílení nebo zeslabení přímého signálu. Účinek příspěvků od různých elementárních zdrojů roviny σ se tak navzájem ruší a při interferenci vlnění v místě příjmu dominuje jen přímá cesta zvuku. Tato rovnováha se poruší, postaví-li se do cesty vlnění překážka. Část elementárních zdrojů roviny σ včetně zdroje na přímé cestě zvuku přestane působit (viz obr. 3) a součet intenzity příspěvků od všech elementárních zdrojů v polorovině σ bude menší v porovnání se stavem bez překážky, kdy by se vlnění ze zdroje Z do místa P mohlo šířit přímo.
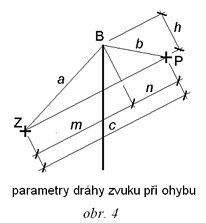
Výpočet útlumu zvuku ohybem využívá mate-matický aparát Fresnelových integrálů. Obecně útlum roste s rozdílem drah zvuku δ [m] - viz vztah ( 1 ) a obr. 4. Roste také s kmitočtem zvuku f [Hz], což je vyjádřeno hodnotou Fresnelova čísla N [-]

kde λ [m] je délka vlny a c0 [m.s-1] je rychlost šíření vlnění. Činitel útlumu d [-] intenzity vlnění při jeho ohybu přes překážku se definuje jako poměr intenzit
![]()
kde I1 resp. I2 [W.m-2] je intenzita zvuku v místě P bez uvažování resp. s uvažováním vlivu clony. Intenzita zvuku je přímo úměrná druhé mocnině efektivní hodnoty akustického tlaku pef [Pa]. Efektivní hodnota je pak přímo úměrná amplitudě akustického tlaku A [Pa] při harmonickém vlnění. Činitel útlumu lze proto vyjádřit jako poměr druhých mocnin amplitud akustického tlaku
![]()
kde A1 resp. A2 [Pa] je amplituda akustického tlaku v místě P bez clony resp. se clonou. Útlum D [dB] hladiny akustického tlaku způsobený clonou bude pak
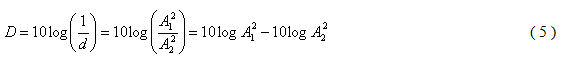
Pro akustický tlak při harmonickém vlnění platí vztah
![]()
kde φ [rad] je fáze. Jako počátek sledování se označí okamžik, kdy vlnění dospělo do místa P po přímé cestě ze zdroje Z. Část akustického tlaku p0 [Pa], která je způsobena jen tímto přímým šířením, lze popsat vztahem
![]()
kde amplituda A0 [Pa] závisí jen na výkonu zdroje a vzdálenosti r [m]. Fáze je nulová, protože na počátku sledování vlnění právě dospělo přímou cestou do místa P a je tedy na počátku vlny. Dalšími cestami volné části roviny (např. i přes bod M - viz obr. 5) dospěje vlnění do bodu P s časovým zpožděním a tedy i v odlišné fázi. Proto lze předpokládat, že akustický tlak p [Pa] v místě P vzniklý jako výsledek spolupůsobení všech cest šíření (přes všechny elementární zdroje volné části roviny σ) bude obsahovat nenulovou fázi φ [rad] a bude tedy odpovídat vztahu ( 6 ). Cílem následujících úvah je stanovit hodnoty amplitud akustického tlaku A1 a A2 [Pa] pro použití ve vztazích ( 4 ) a ( 5 ).
Vztah ( 6 ) lze upravit jako sinus rozdílu dvou úhlů
![]()
Příspěvek dp [Pa] elementární plochy dS [m2] části roviny σ v místě bodu M k hodnotě akustického tlaku v bodě P je

(K dS) [Pa] je amplituda zahrnující vliv A0, δ, ψ, dS
δ / c0 [s] je časové zpoždění vlny vzhledem k počátku sledování.
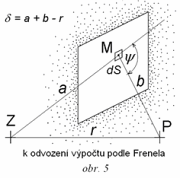
δ = a + b - r [m] je rozdíl drah zvuku mezi dráhou přes bod M a dráhou přímou - viz obr. 5 Vlnové číslo k [rad . m-1] je definováno jako
![]()
Vztah ( 9 ) je možno upravit roznásobením závorky a dosazením vlnového čísla
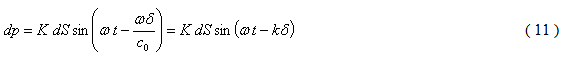
Hodnota akustického tlaku p (Pa) v bodě P se získá integrací přes celou volnou část roviny σ (například přes plochu vyznačenou jako "okno" na obr 5).
![]()
Integrál je možno upravit s využitím vztahu pro sinus rozdílu dvou úhlů
![]()
Integrály ve vztahu ( 13 ) jsou Fresnelovy integrály a označují se

Vztah ( 13 ) pak bude mít tvar
![]()
Porovnáním vztahu ( 15 ) se vztahem ( 8 ) se snadno zjistí že
![]()
Hledanou druhou mocninu amplitudy A [Pa] akustického tlaku v bodě P pak lze stanovit právě pomocí Fresnelových integrálů.
![]()
S přihlédnutím ke vztahům ( 4 ) a ( 5 ) je pak možno pomocí Fresnelových integrálů stanovit činitel d [-] útlumu a útlum D [dB] hladiny akustického tlaku.
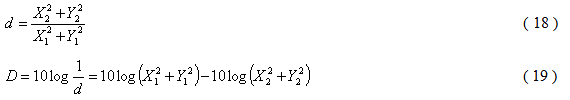
kde X1 a Y1 jsou hodnoty příslušných Fresnelových integrálů stanovené integrací za stavu bez clony tj. po celé rovině σ, X2 a Y2 jsou hodnoty Fresnelových integrálů stanovené integrací jen v rozsahu volné části roviny σ nezakryté clonou.
Při výpočtu Fresnelových integrálů se používá proměnná

kde h [m] je výška trojúhelníka ZBP, m a n [m] jsou úseky základny ZP -viz obr. 4. Fresnelovy integrály se řeší ve tvaru

Hodnoty Fresnelových integrálů lze s potřebnou přesností získat jako součet jistého počtu členů alternující číselné řady. K tomu je však třeba integrály ( 21 ) upravit pomocí substituce
![]()
na tvar

Nová mez v proměnné t v integrálech ( 23 ) je podle vztahu ( 22 )
![]()
a integrály ( 23 ) lze spočítat jako součet konvergentních číselných řad
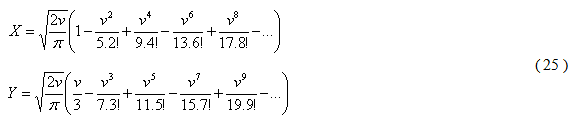
Například pro u = 1 je v = 1,5708 a integrály pak mají hodnoty
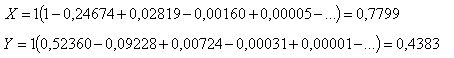
Pro praktické použití lze hodnoty Fresnelových integrálů v závislosti na proměnné u nalézt v tabulce 1.
| u | X | Y | u | X | Y | u | X | Y |
|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,0000 | 0,0000 | 1,50 | 0,4453 | 0,6975 | 3,00 | 0,6057 | 0,4963 |
| 0,05 | 0,0500 | 0,0001 | 1,55 | 0,4018 | 0,6731 | 3,05 | 0,5941 | 0,5445 |
| 0,10 | 0,1000 | 0,0005 | 1,60 | 0,3655 | 0,6389 | 3,10 | 0,5616 | 0,5818 |
| 0,15 | 0,1500 | 0,0018 | 1,65 | 0,3388 | 0,5968 | 3,15 | 0,5154 | 0,5996 |
| 0,20 | 0,1999 | 0,0042 | 1,70 | 0,3238 | 0,5492 | 3,20 | 0,4663 | 0,5933 |
| 0,25 | 0,2498 | 0,0082 | 1,75 | 0,3219 | 0,4994 | 3,25 | 0,4263 | 0,5642 |
| 0,30 | 0,2994 | 0,0141 | 1,80 | 0,3336 | 0,4509 | 3,30 | 0,4057 | 0,5193 |
| 0,35 | 0,3487 | 0,0224 | 1,85 | 0,3584 | 0,4077 | 3,35 | 0,4100 | 0,4700 |
| 0,40 | 0,3975 | 0,0334 | 1,90 | 0,3945 | 0,3733 | 3,40 | 0,4385 | 0,4296 |
| 0,45 | 0,4455 | 0,0474 | 1,95 | 0,4391 | 0,3511 | 3,45 | 0,4835 | 0,4094 |
| 0,50 | 0,4923 | 0,0647 | 2,00 | 0,4883 | 0,3434 | 3,50 | 0,5326 | 0,4152 |
| 0,55 | 0,5377 | 0,0857 | 2,05 | 0,5374 | 0,3513 | 3,55 | 0,5713 | 0,4459 |
| 0,60 | 0,5811 | 0,1105 | 2,10 | 0,5816 | 0,3743 | 3,60 | 0,5880 | 0,4923 |
| 0,65 | 0,6219 | 0,1393 | 2,15 | 0,6159 | 0,4103 | 3,65 | 0,5771 | 0,5404 |
| 0,70 | 0,6597 | 0,1721 | 2,20 | 0,6363 | 0,4557 | 3,70 | 0,5419 | 0,5750 |
| 0,75 | 0,6935 | 0,2089 | 2,25 | 0,6401 | 0,5053 | 3,75 | 0,4936 | 0,5845 |
| 0,80 | 0,7228 | 0,2493 | 2,30 | 0,6266 | 0,5532 | 3,80 | 0,4481 | 0,5656 |
| 0,85 | 0,7469 | 0,2932 | 2,35 | 0,5970 | 0,5931 | 3,85 | 0,4211 | 0,5244 |
| 0,90 | 0,7648 | 0,3398 | 2,40 | 0,5550 | 0,6197 | 3,90 | 0,4223 | 0,4752 |
| 0,95 | 0,7760 | 0,3885 | 2,45 | 0,5061 | 0,6289 | 3,95 | 0,4516 | 0,4357 |
| 1,00 | 0,7799 | 0,4383 | 2,50 | 0,4574 | 0,6192 | 4,00 | 0,4984 | 0,4205 |
| 1,05 | 0,7759 | 0,4880 | 2,55 | 0,4161 | 0,5915 | 4,05 | 0,5452 | 0,4358 |
| 1,10 | 0,7638 | 0,5365 | 2,60 | 0,3889 | 0,5500 | 4,10 | 0,5737 | 0,4758 |
| 1,15 | 0,7436 | 0,5821 | 2,65 | 0,3805 | 0,5011 | 4,15 | 0,5725 | 0,5249 |
| 1,20 | 0,7154 | 0,6234 | 2,70 | 0,3925 | 0,4529 | 4,20 | 0,5417 | 0,5632 |
| 1,25 | 0,6801 | 0,6587 | 2,75 | 0,4233 | 0,4140 | 4,25 | 0,4940 | 0,5746 |
| 1,30 | 0,6386 | 0,6863 | 2,80 | 0,4675 | 0,3915 | 4,30 | 0,4494 | 0,5540 |
| 1,35 | 0,5923 | 0,7050 | 2,85 | 0,5171 | 0,3900 | 4,35 | 0,4276 | 0,5101 |
| 1,40 | 0,5431 | 0,7135 | 2,90 | 0,5624 | 0,4101 | 4,40 | 0,4383 | 0,4623 |
| 1,45 | 0,4933 | 0,7111 | 2,95 | 0,5942 | 0,4481 | 4,45 | 0,4771 | 0,4323 |
Tabulka 1: Hodnoty Fresnelových integrálů
Platí
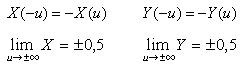
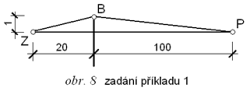
Grafickým vyjádřením hod-not Fresnelových integrálů je křivka klotoida s asymptotickými body (0,5; 0,5) a (-0,5; -0,5), kde u je délka oblouku křivky od počátku (0; 0) k bodu se souřadnicemi (X, Y) - viz obr. 6.
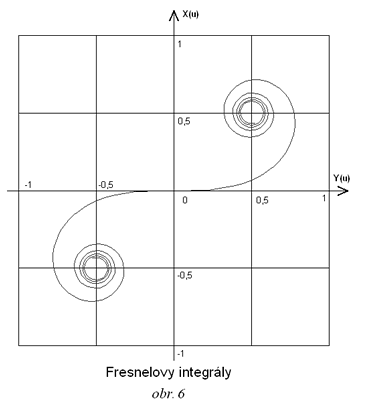
Mezi proměnnou u a rozdílem drah δ = a + b - c existuje tato souvislost popsaná níže - viz obr. 4.
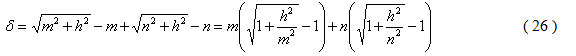
Pro x < 1 platí
![]()
Při praktických aplikacích ohybu zvuku je vždy převýšení h vrcholu překážky významně nižší v porovnání se vzdálenostmi m a n. V takovém případě lze uvažovat jen první dva členy číselné řady ( 27 ) a rovnici ( 26 ) upravit

Fresnelovo číslo N pak za uvedených podmínek bude rovno polovině druhé mocniny proměnné u.
![]()
kde λ [m] je délka vlny.
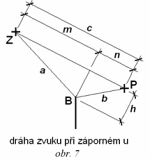
Z diagramu na obr. 6 vyplývá, že útlum zvuku lze stanovit i pro záporné hodnoty proměnné u, kdy výška h trojúhelníka ZBP je záporná. Taková situace nastává v případech, kdy přímá dráha zvuku od zdroje Z k místu příjmu P není clonou přerušena - viz obr. 7. V takovém případě má zápornou hodnotu i rozdíl drah δ = c - a - b a záporné je také Fresnelovo číslo N.
Výpočet útlumu zvuku je možné předvést na příkladech.
Příklad 1: Je třeba spočítat útlum pro zvuk o kmitočtu 1000 Hz při ohybu přes clonu podle obr. 8, kde m = 20 m, n = 100 m a h = 1 m.
Při rychlosti šíření zvukové vlny c0 = 340 m/s má zvuk o kmitočtu 1000 Hz vlno-vou délku λ = 0,34 m. Podle vztahu ( 20 ) je pak u = 0,6
Fresnelovy integrály mají hodnotu
![]()
Útlum se stanoví podle vztahu ( 19 )
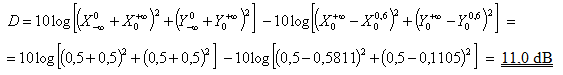
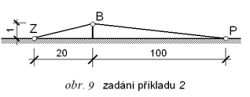
Příklad 2: Je třeba spočítat útlum pro zvuk o kmitočtu 1000 Hz při ohybu přes clonu podle obr. 9, kde m = 20 m, n = 100 m a h = 1 m. Na rozdíl od příkla-du 1 jsou zdroj i místo příjmu zvuku umístěny na terénu. Ohyb zvuku se tak odehrává jen v poloprostoru nad rovinou terénu.
Geometrie příkladu 2 je stejná jako geometrické uspořádání v příkladu 1. Proto bude stejná i hodnota proměnné u = 0,6 a stejné budou i hodnoty Fresnelových integrálů X00,6 = 0,5811 a Y00,6 = 0,1105. Výpočet útlumu ale bude odlišný.
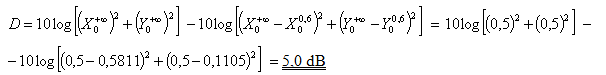
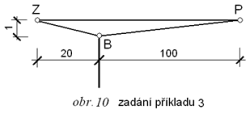
Příklad 3: Je třeba spočítat útlum pro zvuk o kmitočtu 1000 Hz při ohybu přes clonu podle obr. 10, kde m = 20 m, n = 100 m a h = 1 m. Na rozdíl od předchozích příkladů se jedná o případ, kdy clona neprotíná přímou cestu zvuku z bodu Z do bodu P a hodnota u = - 0,6 je v důsledku toho záporná. Záporné budou i hodnoty Fresnelových integrálů X00,6 = 0,5811 a Y00,6 = -0,1105. Výpočet útlumu bude pak
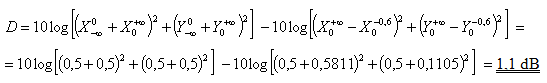
Místo Fresnelových integrálů se v technické praxi používají různé zkrácené metody. Ve výuce akustiky na stavební fakultě ČVUT v Praze se uplatňuje zjednodušující vztah mezi hodnotou Fresnelova čísla N a útlumem D [dB], který navrhl docent Čechura
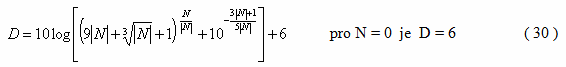
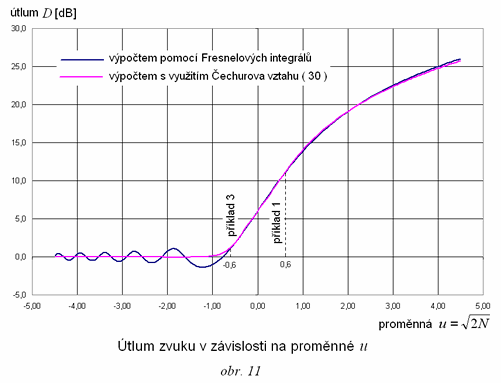
Představu o shodě výsledků mezi přesným výpočtem a výpočtem podle vztahu ( 30 ) podává obr. 11. pro kladné hodnoty u je shoda téměř dokonalá. V oblasti záporných hodnot proměnné u vztah ( 30 ) neakceptuje periodické kolísání hodnot útlumu. V praxi se zřídka kdy řeší útlum tónového zvuku. Běžný zvuk hlučných zařízení je směsí zvuku o velkém počtu kmitočtů, kde spektrum takového zvuku bývá spojité. Zvuk se sleduje a hodnotí v kmitočtových pásmech, nejčastěji oktávových. Útlum D [dB] je závislý na kmitočtu. S kmitočtem se totiž mění hodnota proměnné u resp. hodnota Franalova čísla N. V oblasti záporných hodnot proměnné u jsou tak v každém pásmu zastoupeny kmitočty, které mají útlum kladný, i kmitočty, které mají útlum záporný. Hodnoty útlumu se tak v rámci pásma vyruší, takže útlum v celém pásmu zůstává nulový. Při práci ze zvukem v kmitočtových pásmech tak vztah ( 30 ) poskytuje reálnější hodnoty útlumu v porovnání s přesným výpočtem pomocí Fresnelových integrálů. Řešení výše uvedených příkladů pomocí vztahu ( 30 ) bude:
Příklad 1*
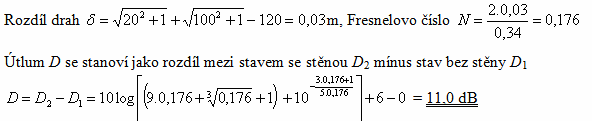
Příklad 2*
Vzhledem k přítomnosti terénu je třeba uvažovat pro útlum D1 při stavu bez stěny nulové Frenelovo číslo N = 0, protože zdroj zvuku Z, vrchol "překážky" B a příjemce zvuku P jsou v jedné přímce. Podle vztahu ( 30 ) je pro N = 0 útlum D1 = 6 dB
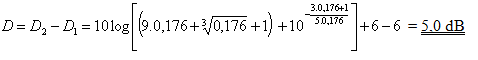
Příklad 3*
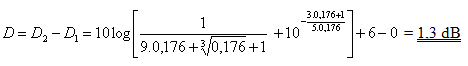
Docent Čechura už nežije, ale měl jsem příležitost nějaký čas s ním působit na stejném pracovišti. Pokud vím, tak vztah ( 30 ) vznikl jako originální odvození doc. Čechury. Domnívám se, že by bylo vhodné o vztahu ( 30 ) hovořit jako o Čechurově vztahu.
Do míst za překážkou v cestě šíření zvuku se zvukové vlny šíří ohybem. Při ohybu dochází ke snížení intenzity zvuku oproti stavu, kdy by v cestě šíření překážka nebyla. Toto snížení nastává dokonce i v místech s nulovou či zápornou hodnotou rozdílu drah zvuku, tj. v místech, odkud lze zdroj zvuku přes překážku pozorovat, jako například ve výše uvedeném příkladu 3 podle obrázku 10. Ohyb zvuku se široce využívá při návrhu protihlukových clon, stěn či bariér při snižování zvuku dopravy i zvuku stacionárních zdrojů. K předpovědi účinku těchto opatření pro stacionární zdroje lze mimo jiné použít i postupy popsané v tomto článku.
Literatura
Beranek, L.L. Noise reduction, McGraw-Hill Book Company, Inc. New York, Toronto, London 1960
Beranek, L.L. Snižování hluku SNTL Praha 1965
Binko, J. Kašpar, I. Fyzika stavebního inženýra, SNTL Praha 1983
Conard, J. Hemond, Jr. Engineering acoustics and noise control, Prentice - Hall 1983
Čechura, J. Stavební fyzika 10 - akustika stavební konstrukcí, ČVUT Praha 1997
Maekawa, Z. Lord, P. Environmental and Architectural Acoustics, E & FN Spon, London 1994
Maekawa, Z. Metodi simplificati per la previsione dell isolamento acustico ottenebile da barriere di vario tipo, Rivista italiana di acustica, 1987
Rektorys, K. a kol. Přehled užité matematiky, Prometheus Praha 1995
The attenuation of sound wave with bends is mostly used in the design of noise walls, curtains and barriers along ways with intensive traffic (roads, rail and tram). Noise reduction from stationary sources with curtains is less common because it is always better to place the noisy device in the machine hall. This is then ventilated through a system with big enough dimensions so as to absorb sound, which then blocks the source of sound and the fan noise. Let's look at some specific installations seen in this context as well as calculations of the sound attenuation bend.