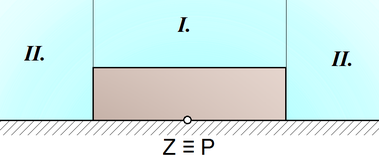
Útlum zvuku stěnou konečné délky
Tento článek navazuje na pojednání [4] z roku 2010. Vlnovou teorii světla a jeho ohyb zdůvodnil francouzský fyzik Augustin Jean Fresnel (1788–1827). Zanedlouho vzpomeneme dvoustého výročí jeho objevu. V roce 1819 získal Fresnel za pojednání o ohybu vlnění cenu Francouzské akademie věd. Útlum vlnění je způsoben interferencí. Zákony ohybu vlnění platí i pro zvuk a lze podle nich řešit i dvourozměrné problémy, tj. útlum zvuku stěnou konečné délky.
Obrázek 1: Elementární zdroje zvuku v rovině
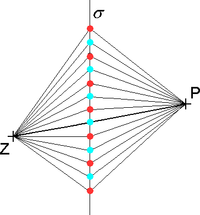
Od bodového zdroje Z se zvukové vlny šíří všemi směry a postupně zasáhnou všechny body roviny σ. Každý bod této roviny kmitá s jinou fází tak, jak k němu vlnění s různým časovým zpožděním dospělo. Každý z těchto bodů je zároveň elementárním zdrojem vlnění, které mimo jiné dospěje i k příjemci zvuku v místě P. Celý soubor elementárních zdrojů zvuku v rovině σ musí mít v místě příjmu stejný účinek jako původní zdroj. Přes různé body roviny σ přichází vlnění do místa příjmu po jiné dráze a tedy s jiným fázovým zpožděním. Vlnění přicházející z místa původního zdroje přímou cestou se skládá s vlněním z jiných směrů, přičemž příspěvky od různých elementárních zdrojů v rovině σ přicházejí do místa příjmu v různé míře se shodnou fází nebo ve fázi opačné a způsobují tak buď zesílení, nebo zeslabení přímého signálu. Na obrázku 1 jsou elementární zdroje zvuku působící zesílení v místě P označeny modře, zdroje působící zeslabení přímého signálu jsou vyznačeny červeně.
Obrázek 2: Kruhové zóny elementárních zdrojů v rovině
Obrázek 3: Schéma průchodu zvuku obdélníkovým otvorem
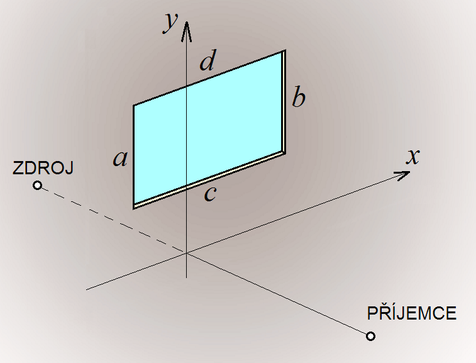
Podrobnější popis vlastností elementárních zdrojů v rovině σ poskytuje obrázek 2. Soubory elementárních zdrojů zvuku v této rovině vytváří kruhové zóny. Modře vyznačené plochy obsahují zdroje, které intenzitu zvuku v místě P zesilují a červeně vyznačená místa jsou zónami elementárních zdrojů, které se podílejí na zeslabení této intenzity. Účinek příspěvků od různých elementárních zdrojů roviny σ se však navzájem ruší a při interferenci vlnění v místě příjmu dominuje jen přímá cesta zvuku. Rovnováha se ale poruší, postaví-li se do cesty vlnění překážka (clona). Část elementárních zdrojů roviny σ je vyřazena z provozu a kromě útlumu zvuku rozptylem akustického výkonu se vzdáleností od zdroje dojde i k útlumu zvuku ohybem. Efektivní hodnotu akustického tlaku p (Pa) v místě pozorování při stínění clonou lze stanovit jako součet příspěvků od všech elementárních zdrojů, které jsou ve volné části roviny σ. Ke stanovení takového součtu slouží Fresnelovy integrály. Obecně je možno předpokládat, že soubor elementárních zdrojů zvuku vyplňuje volný otvor „okno“ tvaru obdélníka, jak ukazuje obrázek 3.
V článku [4] bylo naznačeno odvození Fresnelových integrálů X a Y. Tam také bylo pojednáno o stanovení jejich hodnot. Efektivní hodnota akustického tlaku ve sledovaném místě P při volném šíření zvuku (bez jakékoli překážky) se označí p0 (Pa). Relativní akustický tlak q = p/p0 (–) lze vyjádřit v komplexním tvaru pomocí Fresnelových integrálů.
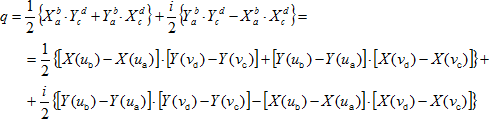(1)
kde u (–) je proměnná pro integraci ve vodorovném směru a v (–) je obdobná proměnná pro integraci ve směru svislém. Hodnotu těchto proměnných lze vypočítat podle vztahu (20) z článku [4]. Integrační meze ve vodorovném směru jsou ua a ub a integrační meze ve směru svislém jsou vc a vd. Činitel útlumu intenzity vlnění d0 (–) lze získat jako součet druhé mocniny reálné a druhé mocniny imaginární složky relativního akustického tlaku.
(2)
Dosud prezentovaný výpočet činitele útlumu d0 (–) uvažoval s volným prostorem při přímém šíření vlnění jako s výchozím stavem. V reálných situacích ale výchozí stav už obsahuje nějaké stínění. Například může být výchozí stav omezen jen na část roviny σ nad terénem. Proto je třeba nově definovat činitele útlumu d (–) způsobem, který bude jako výchozí stav uvažovat reálnou situaci před realizací protihlukové clony, jejíž účinek je třeba výpočtem předpovědět.
(3)
kde d01 (–) je podle vztahu (2) činitel útlumu intenzity vlnění pro výchozí stav a d02 (–) je podle stejného vztahu činitel útlumu intenzity vlnění pro stav s realizovanou clonou.
Útlum ohybem se pak stanoví podle vztahu (4).
(4)
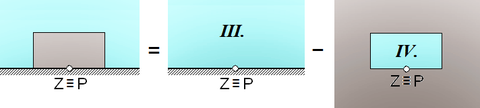
Složitější tvary clon je možno vyskládat z dílčích částí roviny σ. Sčítají se hodnoty relativního akustického tlaku q (−). Činitel útlumu d0 (−) se stanoví jako součet druhé mocniny součtu reálných a druhé mocniny součtu imaginárních složek relativního akustického tlaku.
,
(5)
kde n je počet sčítaných částí roviny σ. Použití uvedené metody výpočtu je možno ilustrovat na příkladech.
Příklad číslo 1
Obrázek 4: Schéma k příkladu číslo 1
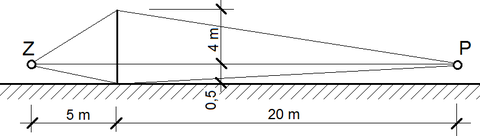
Zdroj Z i místo příjmu P zvuku se nacházejí 0,5 m nad terénem a jsou odděleny clonou výšky 4,5 m umístěnou ve vzdálenosti 5 m od zdroje a 20 m od příjemce. Clona je velmi dlouhá, takže její délku je možno uvažovat jako nekonečnou. Pro zvuk o kmitočtu 250 Hz je třeba stanovit útlum způsobený ohybem vlnění přes korunu clony.
a) řešení stavu po realizaci clony
Vlnová délka zvuku je λ = 340/250 = 1,36 m. Stanoví se hodnota proměnné vc .
Hodnoty všech proměnných a Fresnelových integrálů jsou uvedeny v tabulce
| ua = −∞ | X(ua) = −0,5 | Y(ua) = −0,5 |
| ub = +∞ | X(ub) = +0,5 | Y(ub) = +0,5 |
| vc = 2,425 | X(uc) = 0,5310 | Y(uc) = 0,6266 |
| vd = +∞ | X(ud) = +0,5 | Y(ud) = +0,5 |
Činitel útlumu pro stav po realizaci clony se získá dosazením do vztahu (2)
b) řešení stavu před realizací clony
Hodnoty proměnných a Fresnelových integrálů jsou uvedeny v tabulce
| ua = −∞ | X(ua) = −0,5 | Y(ua) = −0,5 |
| ub = +∞ | X(ub) = +0,5 | Y(ub) = +0,5 |
| vc = −0,303 | X(uc) = −0,3024 | Y(uc) = −0,0145 |
| vd = +∞ | X(ud) = +0,5 | Y(ud) = +0,5 |
Činitel útlumu pro stav před realizací clony se získá dosazením do vztahu (2)
Výsledný činitel útlumu clonou se získá dosazením do vztahu (4)
a útlum dosazením do vztahu (5).
dB
Byl stanoven útlum zvuku ohybem přes korunu zadané clony D = 17,3 dB.
Příklad číslo 2
Obrázek 5: Schéma k příkladu číslo 2
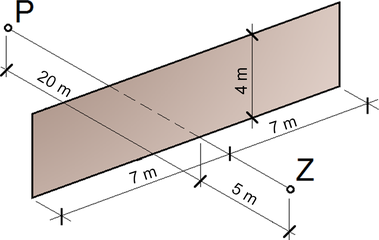
Zdroj zvuku Z i jeho příjemce P se nacházejí na terénu a jsou odděleny clonou výšky 4 m umístěnou ve vzdálenosti 5 m od zdroje a 20 m od příjemce. Clona je ukončena ve vzdálenosti 7 m nalevo i napravo od spojnice mezi zdrojem a pozorovatelem. Pro zvuk o kmitočtu 250 Hz je třeba stanovit útlum způsobený ohybem vlnění přes korunu i boky clony.
Nejdříve bude užitečné stanovit hodnoty některých proměnných. Pro šíření zvuku přes vrchol clony se stanoví proměnná
Pro šíření zvuku přes boky clony lze využít souměrnosti
a) řešení stavu po realizaci clony
Obrázek 6: Schéma rozdělení volného prostoru kolem clony k příkladu 2
Činitel útlumu bude je třeba stanovit jako součet dílčích částí roviny σ podle vztahu (5). Řešení se může ubírat několika různými cestami vedoucími ke správnému výsledku. Jednu z možností naznačuje obrázek 6.
Výsledný relativní akustický tlak vznikne jako součet q = qI + 2qII, kde qI (−) resp. qII (−) je relativní akustický tlak způsobený elementárními zdroji z části roviny σ nad clonou resp. vedle clony.
Hodnoty proměnných a Fresnelových integrálů pro stanovení relativního tlaku qI (−) jsou v tabulce.
| ua = −4,244 | X(ua) = −0,4986 | Y(ua) = −0,5750 |
| ub = 4,244 | X(ub) = 0,4986 | Y(ub) = 0,5750 |
| vc = 2,425 | X(uc) = 0,5310 | Y(uc) = 0,6266 |
| vd = +∞ | X(ud) = +0,5 | Y(ud) = +0,5 |
Hodnota relativního akustického tlaku se získá dosazením do vztahu (1)
Hodnoty proměnných a Fresnelových integrálů pro stanovení relativního tlaku qII (−) jsou v tabulce. Z obou totožných částí II roviny σ výpočet bere v úvahu tu, která se na obrázku (6) vyskytuje vpravo.
| ua = 4,244 | X(ua) = 0,4986 | Y(ua) = 0,5750 |
| ub = +∞ | X(ub) = 0,5 | Y(ub) = 0,5 |
| vc = 0 | X(uc) = 0 | Y(uc) = 0 |
| vd = +∞ | X(ud) = +0,5 | Y(ud) = +0,5 |
Hodnota relativního akustického tlaku se získá dosazením do vztahu (1)
Výsledný činitel útlumu se stanoví podle vztahu (5)
a) řešení stavu před realizací clony
Jedná se o polorovinu nad terénem. Hodnoty proměnných a Fresnelových integrálů jsou uvedeny v tabulce
| ua = −∞ | X(ua) = −0,5 | Y(ua) = −0,5 |
| ub = +∞ | X(ub) = +0,5 | Y(ub) = +0,5 |
| vc = −0 | X(uc) = 0 | Y(uc) = 0 |
| vd = +∞ | X(ud) = +0,5 | Y(ud) = +0,5 |
Hodnota činitele útlumu se získá dosazením do vztahu (2)
Činitel útlumu clonou postavenou na terénu se získá ze vztahu (4)
a útlum dosazením do vztahu (5).
dB
Byl stanoven útlum ohybem zvuku přes zadanou clonu konečné délky D = 10,4 dB.
Příklad číslo 3
Obrázek 7: Schéma rozdělení volného prostoru kolem clony k příkladu 3
Zadání příkladu číslo 2 bude řešeno odlišným způsobem podle schématu na obrázku 7. Výsledný útlum se získá odečtením plochy stěny od poloroviny nad terénem.
Hodnoty proměnných a Fresnelových integrálů byly již stanoveny v příkladu číslo 2. Jiné však bude uspořádání dalšího výpočtu.
a) řešení stavu po realizaci clony
Řešení poloroviny nad terénem bylo již rovněž provedeno v příkladu číslo 2. Hodnota relativního akustického tlaku byla získána ze vztahu (1)
V dalším bude proveden výpočet činitele útlumu způsobeného šířením zvuku přes otvor (okno), jehož rozměry jsou dány rozměry clony. Hodnoty proměnných a Fresnelových integrálů jsou uvedeny v tabulce
| ua = −4,244 | X(ua) = −0,4986 | Y(ua) = −0,5750 |
| ub = 4,244 | X(ub) = 0,4986 | Y(ub) = 0,5750 |
| vc = 0 | X(uc) = 0 | Y(uc) = 0 |
| vd = 2,425 | X(ud) = 0,5310 | Y(ud) = 0,6266 |
Hodnota relativního akustického tlaku se získá dosazením do vztahu (1)
Výsledný činitel útlumu se stanoví podle vztahu (5)
Další postup je už shodný s příkladem číslo 2. Činitel útlumu clonou postavenou na terénu se získá ze vztahu (4)
a útlum dosazením do vztahu (5).
dB
Byl stanoven útlum ohybem zvuku přes zadanou clonu konečné délky D = 10,4 dB. Výsledek se shoduje s výsledkem příkladu číslo 2.
Závěr
Obrázek 8: Útlum zvuku ohybem v okolí ukončení clony
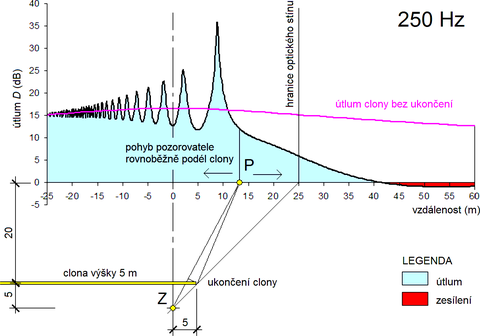
Na obrázku 8 je pro kmitočet 250 Hz vyznačen útlum zvuku v závislosti na poloze pozorovatele v okolí ukončení clony. Pozorovatel i zdroj zvuku jsou umístěni na terénu. Clona je vysoká 5 m. Pozorovatel se pohybuje rovnoběžně podél této clony ve vzdálenosti 20 m od ní. Je třeba upozornit, že je vyznačen jen útlum způsobený koincidencí vlnění, tedy bez vlivu útlumu, který by měl být způsoben disperzí akustického výkonu v důsledku proměnné vzdálenosti pozorovatele od zdroje. V důsledku koincidence mají oscilace útlumu pro každý kmitočet jiný tvar. Proto je lze pozorovat jen v případě, má-li zvuk tónové složky. Ve stavební a urbanistické akustice se zvuk obvykle sleduje a hodnotí v oktávových pásmech. Použití jen středního kmitočtu oktávy při výpočtu tak může vést k chybám až několik decibelů zejména při nevyrovnaném spektru nebo dokonce při přítomnosti tónového zvuku. Přesnější výsledek může poskytnout úzkopásmová analýza. Ta je dnes při použití vyspělé výpočetní techniky realizovatelná. Nejsou však k dispozici údaje o hladinách akustického výkonu zdrojů zvuku v úzkých pásmech. Při současném stupni vývoje zvukoměrné techniky však ani toto nemusí být neřešitelný problém.
Literatura
- Binko, J. Kašpar, I. Fyzika stavebního inženýra, SNTL Praha 1983
- Conard, J. Hemond, Jr. Engineering acoustics and noise control, Prentice – Hall 1983
- Čechura, J. Stavební fyzika 10 – akustika stavebních konstrukcí, ČVUT Praha 1997
- Kaňka, J: O výpočtech útlumu zvuku ohybem, TZB-info 5. 7. 2010
- Komrska, J: Fourierovské metody v teorii difrakce a ve strukturní analýze. VUTIUM Brno, 2001.
- Maekawa, Z. Lord, P. Environmental and Architectural Acoustics, E & FN Spon, London 1994
- Maekawa, Z. Metodi simplificati per la previsione dell isolamento acustico ottenebile da barriere di vario tipo, Rivista italiana di acustica,1987
- Rektorys, K. a kol. Přehled užité matematiky, Prometheus Praha 1995
This article continues the discussion [4] from 2010. The wave theory light and of its diffraction was substantiated by French physicist Augustin-Jean Fresnel (l788–1827). Soon we will recall the bicentennial of his discovery. In 1819 Fresnel received Prize of the French Academy of Sciences for discussion of wave diffraction. Wave attenuation is caused by interference. Laws of wave diffraction also apply to the sound. According to them two-dimensional problem i.e. the sound attenuation of a wall with finite length can be solved.