Požární ochrana oceli dřevem a materiály na bázi dřeva: FE modely (část 3.)
Přehrát audio verzi
Požární ochrana oceli dřevem a materiály na bázi dřeva: FE modely (část 3.)
00:00
00:00
1x
- 0.25x
- 0.5x
- 0.75x
- 1x
- 1.25x
- 1.5x
- 2x
Třetí část série se zaměřuje na numerické modelování chování ocelového nosníku chráněného OSB obkladem pomocí metody konečných prvků (FE). V první fázi byla provedena tepelná analýza, která detailně popisovala přenos tepla, zahrnula materiálové vlastnosti OSB a zohlednila podmíněné odpadnutí obkladu. Následná mechanická analýza navázala na výsledky tepelné simulace a umožnila posoudit deformace a únosnost ocelového prvku při zvýšených teplotách. Výpočty byly provedeny v prostředí ANSYS Mechanical, přičemž výsledky ukázaly dobrou shodu s experimentálními daty, zejména do okamžiku selhání obkladu. Odchylky se projevily v pozdější fázi, kdy modely nezahrnovaly viskoplastické chování oceli ani explicitní simulaci poruchy obkladu. Studie potvrzuje, že FEA modelování je vhodným nástrojem pro návrh požární ochrany, avšak vyžaduje doplnění o pokročilejší materiálové modely a simulaci dynamického selhání.
1. Úvod
Pro ověření výsledků experimentálního měření a numerických CFD simulací byla problematika dále analyzována pomocí metody konečných prvků (FE). V rámci této analýzy byly vytvořeny modely pro tepelnou a následně mechanickou odezvu ocelového nosníku chráněného OSB obkladem při požárním zatížení. V tepelné analýze byla věnována zvláštní pozornost modelování přenosu tepla, zahrnutí materiálových vlastností OSB a simulaci teplotně či časově podmíněného odpadnutí obkladu. Mechanická část výpočtu navazovala na výsledky tepelné analýzy a umožnila posouzení chování oceli v závislosti na jejím ohřevu, především z hlediska průhybů. Tento přístup umožnil nejen porovnání s naměřenými hodnotami, ale také identifikaci limitů současných výpočetních metod, zejména v souvislosti s nemožností plně zachytit progresivní odpadávání obkladu. Uvedený text představuje pouze stručné shrnutí mechanických modelů; pro detailnější popis je vhodné nahlédnout do [1, 2].
2. FEA model – tepelná analýza
Pro ověření výsledků experimentů a numerických CFD simulací byla vytvořena samostatná sada výpočtů metodou konečných prvků (FE) v programu ANSYS Mechanical, zaměřená na detailní popis teplotního chování ocelového nosníku chráněného OSB obkladem při požáru. Z důvodu snížení výpočetní náročnosti byla v počáteční fázi provedena citlivostní analýza na dvourozměrných řezech modelu. Tyto řezy byly zvoleny přesně v místech, kde byly v reálném experimentu umístěny termočlánky, aby bylo možné dosáhnout co nejpřesnějšího porovnání výsledků. Tímto přístupem bylo možné rychle otestovat vliv jednotlivých parametrů na výsledky a zároveň zkrátit dobu výpočtu.
Po optimalizaci nastavení byla citlivostní analýza ukončena a výpočty byly provedeny na plnohodnotném třírozměrném modelu. Ten posloužil nejen k vyhodnocení tepelného působení, ale i jako vstup pro navazující mechanickou analýzu únosnosti nosníku při zvýšených teplotách. V počáteční fázi modelování byla použita přednastavená hrubší výpočetní síť, aby se ověřila stabilita výpočtu a aby se odstranily možné chyby v geometrii nebo definici okrajových podmínek. Postupným zpřesňováním byla vytvořena finální síť o celkovém počtu 111 093 uzlů a 19 822 prvků (Obr. 1), která poskytla vyvážený poměr mezi přesností výsledků a časovou náročností výpočtu.

Obr. 1: Finální tvar výpočetní sítě pro FEA model ocelového nosníku s jednovrstvým obkladem
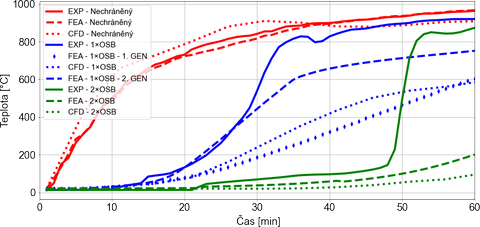
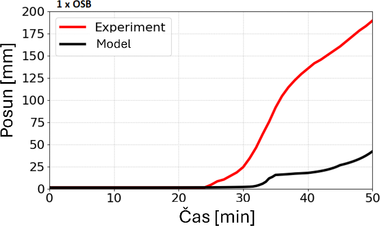
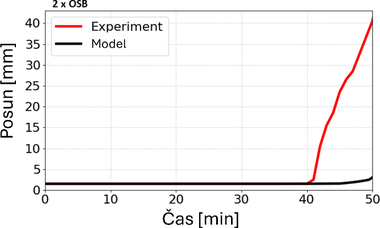
Okrajové podmínky byly stanoveny na základě dříve publikovaných výsledků [1, 2], a to včetně kombinovaného působení konvekce a radiace. Součinitel přestupu tepla prouděním byl uvažován 50 kW/m² a povrchová emisivita OSB obkladu byla nastavena na hodnotu 0,93 (zohledňující zuhelnatění, norma udává hodnotu 0,7). Tato vysoká emisivita odráží tmavé zbarvení zuhelnatělé vrstvy OSB po vystavení požáru a byla ověřena variantními simulacemi s různými hodnotami, jejichž výsledky byly vzájemně porovnávány. Naměřené teploty z deskových snímačů teploty, rozmístěných během experimentu po třech stranách nosníků, byly použity k definici tepelného zatížení na povrchu modelu. Tento postup zajistil, že výpočty vycházely z reálných okrajových podmínek odpovídajících experimentu, a umožnil přímé porovnání výsledků s CFD modelem. Srovnání ukázalo (viz Obr. 2), že v modelech FEA docházelo k mírnému posunu průběhu ohřevu ocelového prvku, což se promítlo do zvýšení odhadované požární odolnosti až o 15 minut ve srovnání se základní variantou, tj. nechráněným nosníkem. V tzv. modelech 2. generace, kde byl do výpočtu zahrnut jev odpadnutí obkladu, byly po jeho poruše předefinovány okrajové podmínky tak, aby teploty působily přímo na povrch oceli a nikoliv přes fiktivní zbytkovou vrstvu odhořelého materiálu. Tento postup umožnil realističtější simulaci následného rychlého ohřevu a vedl k lepší shodě s experimentálními výsledky (viz Obr. 2).
Výsledky ukázaly dva charakteristické jevy. První z nich odpovídal době plné funkčnosti OSB obkladu, kdy se rozdíl mezi modelem 2. gen. a experimentem pohyboval kolem 80 °C. Tento rozdíl lze vysvětlit použitím standardních materiálových charakteristik OSB, zejména hodnot tepelné kapacity, která má v této fázi významný vliv na rychlost ohřevu. Porovnání s CFD modelem, v němž byla zahrnuta tepelná degradace OSB a tím i teplotně zá-vislý pokles hustoty materiálu, ukázalo, že právě vývoj hustoty OSB v závislosti na teplotě je nutné v budoucím výzkumu podrobněji řešit.
Druhý charakteristický stav nastal v okamžiku „odhoření“ OSB obkladu (tedy OSB již z větší části shořelo, ale stále neodpadlo a plní ochranou funkci), po přibližně 15 minutách u jednovrstvé varianty a po 47 minutách u dvouvrstvé. Při postupném selhávání docházelo k odlepování obkladu zejména ve spárách, což vedlo k lokálnímu zvýšení teploty oceli. Po úplném odpadnutí obkladu nastal prudký ohřev, který implicitní výpočetní modely nedokázaly plně zachytit (bylo by potřeba upravit modely na explicitní typ).
Pro realistické zahrnutí poruchy OSB byl proto FEA model upraven na explicitní výpočetní postup (model 2. gen.). V této verzi byl čas poruchy u jednovrstvého OSB obkladu o tloušťce 22 mm stanoven na 21,5 minut y. V modelu byla v tomto okamžiku odstraněna ochranná vrstva a nově definováno tepelné zatížení na odhalený povrch oceli.
Rozdíly mezi vypočtenými a naměřenými teplotami před selháním OSB lze částečně přičíst nezohlednění konstrukční spáry umístěné přibližně v jedné třetině délky nosníku od stěny pece. Během experimentu došlo k jejímu otevření, což způsobilo lokální přehřátí oceli a následné zvýšení teploty v celém nosníku díky vedení tepla. Tento jev bude nutné v budoucím vývoji pokročilého modelu zohlednit, aby bylo možné dosáhnout ještě vyšší shody mezi simulací a reálným průběhem experimentu.
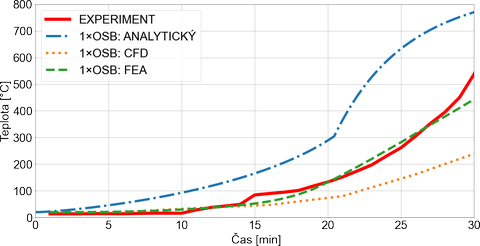
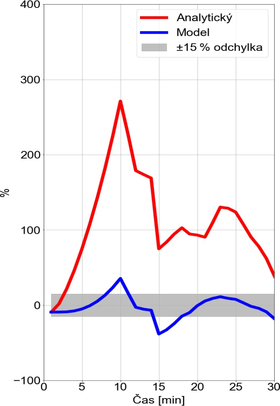
Současně bylo provedeno i srovnání s analytickým výpočtem využívající přírůstkovou metodu, jehož výsledky jsou uvedeny na Obr. 3 a Obr. 4, které ukazuje významné rozdíly v predikci teplotního nárůstu oproti experimentu. Je důležité poznamenat, že i analitický postup dává bezpečné výsleky, ale velmi konzervativní.
4. FEA model – mechanická analýza
Mechanická analýza byla provedena v návaznosti na výsledky tepelné analýzy s cílem posoudit deformace ocelového nosníku chráněného OSB obkladem při požáru. Postup vycházel z rámce definovaného v Eurokódu 3 [3], přičemž výpočetní přístup byl rozšířen o údaje z experimentu a teplotní pole získané v předchozí části modelování. Tímto způsobem bylo možné přímo zohlednit reálný průběh ohřevu oceli a přenést jej do následné mechanické odezvy.
Geometrie modelu odpovídala prostému nosníku délky 3500 mm, zatíženému uprostřed rozpětí silou 982 N (Obr. 5). Tomu odpovídal maximální ohybový moment přibližně 0,86 kNm. U profilu SHS 100×6 tak vzniklo maximální napětí asi 12,9 MPa, což představuje přibližně 5,5 % meze kluzu oceli třídy S235. Tento statický model byl zvolen tak, aby co nejvěrněji odpovídal podmínkám velkorozměrového experimentu, kdy byly nosníky uloženy prostě na dvou podporách vytvořených pomocí volného a pevného válečku a zatíženy bodovým břemenem, reprezentujícím skutečné provozní zatížení. Tím byla zajištěna přímočará interpretace naměřených průhybů a jejich následné porovnání s výsledky výpočtů.
Jako klíčový vstupní parametr byla do mechanické analýzy vložena teplotní pole získaná z tepelné analýzy, validovaná proti experimentálním datům. Tyto teploty byly přiřazeny jednotlivým prvkům sítě, čímž došlo k teplotně závislé degradaci mechanických vlastností oceli. Mechanické vlastnosti oceli, modul pružnosti, mez kluzu, mez proporcionality a redukční faktory v závislosti na teplotě, byly převzaty z Eurokódu 3 [3]. Vlastnosti OSB panelů byly uvažovány dle Eurokódu 5 [4], avšak jejich přímý příspěvek k únosnosti byl zanedbán, protože v reálné konstrukci působí pouze jako ochranný prvek, nikoli jako nosný materiál.
Výpočty byly provedeny metodou konečných prvků v prostředí ANSYS Mechanical, a to s implicitním řešením, které je pro tento typ úloh běžně používáno. Před vlastní analýzou byla provedena citlivostní studie zaměřená na vliv velikosti výpočetního kroku a hustoty výpočetní sítě na přesnost výsledků. Bylo zjištěno, že příliš hrubá síť vede k podhodnocení lokálních maxim průhybu a může zkreslit dynamiku poklesu tuhosti při teplotách nad 500 °C. Naopak příliš jemná síť prodlužuje výpočetní čas, aniž by přinášela úměrné zvýšení přesnosti. Na základě těchto poznatků byla zvolena síť s optimalizovaným počtem prvků (kompromis mezi výpočetním časem, a přesností v místech modelu, která nemají na výsledek chování konstrukce) a krokem řešení odpovídajícím 5 sekundám reálného času.
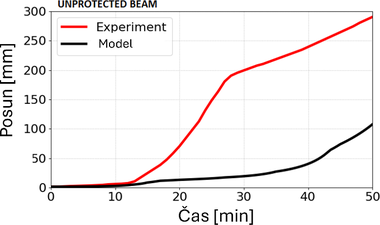
Výsledky ukázaly, že po dosažení teploty přibližně 600 °C dochází k prudké změně mechanického chování oceli, což se projevuje výrazným nárůstem průhybů (Obr. 6). Tento jev je v souladu se známým fyzikálním mechanismem poklesu modulu pružnosti a meze kluzu oceli při vysokých teplotách. Porovnání s experimentem však odhalilo, že průhyby vypočtené na základě Eurokódu 3 byly systematicky nižší než hodnoty naměřené, a to zejména v pozdější fázi zkoušky. Tento rozdíl je možné vysvětlit absencí viskoplastického přetváření oceli, které má při teplotách nad 500–550 °C zásadní vliv na deformace konstrukce.
Podobné závěry byly publikovány již dříve [5], kde bylo zdůrazněno, že standardní materiálové modely obsažené v Eurokódu 3 vycházejí z krátkodobých zkoušek a nejsou schopny přesně popsat dlouhodobé teplotní namáhání, zejména v oblasti plně plastického chování. Při modelování do teplot cca 600 °C lze pro základní odhady použít publikované materiálové křivky (např. [5]), avšak pro vyšší teploty a delší expozice je nutné zohlednit viskoplastické chování a časově závislou ztrátu tuhosti pomocí pokročilých materiálových modelů.
Numerické simulace rovněž ukázaly, že nerovnoměrný ohřev nosníku po jeho délce měl v konkrétních podmínkách experimentu jen omezený vliv na výsledný průhyb, což je důležité pro zjednodušené modely. Naopak lokální selhání OSB obkladu, zaznamenané při experimentu, vedlo k prudkému zvýšení teploty oceli v odhalené části a následně k rychlému nárůstu deformace, což model bez explicitní simulace poruchy obkladu nedokázal plně zachytit.
Výsledky porovnání experimentu a simulace potvrzují, že i přes konzervativní charakter výpočtu dle Eurokódu 3 (podhodnocení průhybu) je pro praktický návrh uvažující návrhové teploty nad 600 °C nutné zohlednit viskoplastické chování oceli a reálné chování ochranného obkladu v čase. Při vhodném doplnění modelu o tyto aspekty lze teoreticky dosáhnout shody s experimentálními daty a získat tak nástroj použitelný pro predikci chování chráněných ocelových konstrukcí v požáru.
Souvislosti a pokračování
Tento článek představuje základ pro sérii článků na téma požární ochrana oceli OSB obkladem, které se detailněji věnují:
- Část 1 – Historie a základy
- Část 2 – Požární experiment a CFD modely
- Část 4 – Diskuse nad výsledky a možnosti použití s ohledem na Požární kodex norem
Prohlášení o původu výsledků
Vybrané výsledky, metody a závěry uvedené v tomto článku byly již publikovány v odborném časopise Fire and Materials:
- Šejna, J. et. al. (2025). Fire Protection of Steel Beam by OSB Claddings—A Fire Experiment and Numerical Models. Fire and Materials. https://doi.org/10.1002/fam.3260
Zároveň jsou výsledky součástí disertační práce Ing. Jakuba Šejny, obhájené na Fakultě stavební ČVUT v Praze v roce 2025, s názvem Požární ochrana ocelových konstrukcí pomocí dřeva a materiálů na bázi dřeva.
5. Literatura
- ŠEJNA, protected by OSB. In: Engineering Mechanics 2022. Prague: Institute of Theoretical and Applied Mechanics, AS CR, s. 365–368. ISBN 978-80-86246-51-2. ISSN 1805-8256.
- ŠULC, S., ŠEJNA, J., ŠMILAUER, V. a WALD, F., 2022. Steel elements with timber fire protection – experiment and numerical analysis. Acta Polytechnica CTU Proceedings, 34. ISSN 2336-5382. Dostupné z:
https://doi.org/10.14311/APP.2022.34.0116. - EN 1993-1-2, 2005. Eurocode 3: Design of steel structures – Part 1-2: General rules – Structural fire design. EU: The European Union per Regulation.
- EN 1995-1-2, 2004. Eurocode 5: Design of timber structures – Part 1-2: General – Structural fire design. EU: The European Union per Regulation.
- WALD, F., BURGESS, I., KWASNIEWSKI, L., HOROVÁ, K. a CALDOVÁ, E., 2014. Benchmark studies: Experimental validation of numerical models in fire engineering. Prague: CTU Publishing House, Czech Technical University in Prague. ISBN 978-80-01-05443-7.
The third part of the series focuses on numerical modeling of a steel beam protected by OSB cladding using the Finite Element (FE) method. The first stage involved thermal analysis, which described heat transfer in detail, included the material properties of OSB, and accounted for condition-dependent cladding detachment. The subsequent mechanical analysis, based on the thermal results, enabled assessment of deformations and load-bearing capacity of the steel member at elevated temperatures. Simulations were carried out in ANSYS Mechanical, showing good agreement with experimental data, particularly up to the moment of cladding failure. Deviations appeared in later stages, as the models did not incorporate viscoplastic steel behavior or explicit simulation of cladding failure. The study confirms that FEA modeling is a suitable tool for designing fire protection, but requires further development with advanced material models and dynamic failure simulation.