Dimenzování vzduchospalinových cest krbů
Návrh vzduchospalinové cesty pro krb spalující dřevo je založen na spalovacích rovnicích, odvození vztahů pro určení přísunu paliva-dřeva, průtoku spalovacího vzduchu a průtoku spalin. Pro názornost je uveden konkrétní příklad výpočtu.
Spalovací rovnice dřeva
Složení dřeva
Pro všechny výpočty se bude uvažovat tzv. standardní hmotnostní složení suchého dřeva, neboli sušiny. Je dáno poměrnou hmotností prvků v sušině vztaženou k hmotnosti sušiny (kg.kg-1), čili poměrem M / Ms, což lze také vyjádřit hmotnostní koncentrací prvků (-) f = M / Ms.
Hmotnostní koncentrace prvků (-) standardního suchého dřeva jsou uvedeny v prvním sloupci. Znamenají také hmotnosti prvků (kg) v 1 kg suchého dřeva.
| - uhlíku C | fCs | = 0,5 | fCd | = 0,4, |
| - vodíku H2 | fH2s | = 0,056 | fH2d | = 0,048, |
| - kyslíku O2 | fO2s | = 0,44 | fO2d | = 0,352, |
| - vody H2O | fH2Os | = 0 | fH2Od | = 0,2, |
| celkem | fs | = 1,0 | fd | = 1,0. |
V tomto příspěvku bude uvažováno se standardním dřevem o poměrné hmotnostní vlhkosti 0,2, což je 20 %. Protože poměrná hmotnost sušiny v 1 kg vlhkého dřeva je snížena vlivem přítomnosti vody na 0,8 kg.kg-1, klesnou koncentrace prvků také na 0,8 násobek původních koncentrací v suchém dřevě, což je uvedeno ve druhém sloupci. Takže např. platí, že fCd = 0,8 . fCs = 0,8 . 0,5 = 0,4 nebo také 0,4 kg.kg-1.
Spalování suchého dřeva
Do spalovacích rovnic prvků suchého dřeva vstupují látková množství v kmol. Jsou to takové soubory atomů dané látky, jejichž hmotnost v kg se číselně rovná relativní atomové hmotnosti látky. Takže spalování uhlíku C probíhá podle vztahu
C + O2 = CO2
12 kg C + 2 . 16 kg O2 = 44 kg CO2
1 kg C + 2,67 kg O2 = 3,67 kg CO2
Ze vztahu vyplývá, že pro spálení 1 kg C (uhlíku) je zapotřebí MO2-C = 2,67 kg O2 (kyslíku), přičemž vznikne MCO2-C = 3,67 kg CO2 (oxidu uhličitého).
Spalování vodíku H2 probíhá podle vztahu
2 H2 + O2 = 2 H2O
2 . 2 kg H2 + 32 kg O2 = 36 kg H2O
1 kg H2 + 8 kg O2 = 9 kg H2O
Ze vztahu vyplývá, že pro spálení 1 kg H2 (vodíku) je zapotřebí MO2-H2 = 8 kg O2 (kyslíku), přičemž vznikne MH2O-H2 = 9 kg H2O (vodní páry).
Spalování vlhkého dřeva
Ve všech dalších výpočtech se bude uvažovat s poměrnou hmotnostní vlhkostí dřeva 0,2 a se součinitelem přebytku vzduchu λ = 2.
Teoretická poměrná potřeba kyslíku O2 (λ = 1) vztažená na 1 kg vlhkého dřeva
MO2p = fCd . MO2-C + fH2d . MO2-H2 - MO2d = 0,4 . 2,67 + 0,048 . 8 - 0,352 = 1,1 kg.kg-1.
Poslední člen představuje odpočet množství kyslíku O2 již obsaženého ve dřevě.
Teoretická poměrná potřeba vzduchu (λ = 1) vztažená na 1 kg vlhkého dřeva
![]()
kde hmotnostní podíl rO2 (-) je dán vztahem (10).
Skutečná poměrná potřeba vzduchu (λ = 2) vztažená na 1 kg vlhkého dřeva
![]()
Složení skutečných spalin
Hmotnostní složení skutečných spalin M / Ma (kg.kg-1) nebo (-) je dáno pro:
| - oxid uhličitý CO2 | fCd . MCO2-C | = 0,4 . 3,67 | = 1,468, |
| - vodní páru z vodíku | fH2d . MH2O-H2 | = 0,048 . 9 | = 0,432, |
| - vodní páru z vody | fH2Od . Md | = 0,2 . 1 | = 0,200, |
| - dusík zbylý ze vzduchu | Mvtp - MO2p | = 4,72 - 1,1 | = 3,620, |
| - přebytek vzduchu (λ = 2) | Mvp - Mvtp | = 9,44 - 4,72 | = 4,720, |
| celkem skutečné spaliny | Ma | = 10,440 kg.kg-1. |
Poměrné hmotnostní množství spalin vztažené k hmotnosti dřeva je dáno vztahem
![]()
Bilance tepelných výkonů u krbu
Při výpočtovém stavu vstupují do krbu (obr. 1) tepelné příkony obsažené v palivu-dřevu a ve spalovacím vzduchu. Z krbu vystupuje jednak výpočtový tepelný výkon směřující do vytápěného prostoru, jednak tepelná ztráta spalinami do komína.
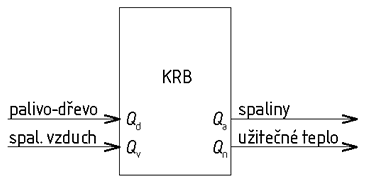
Obr. 1 - Bilance tepelných výkonů u krbu
Z bilance výkonů platí vztah
![]()
Qd je tepelný příkon daný přísunem dřeva (W)
Qv - tepelný příkon obsažený ve spalovacím vzduchu (W)
Qn - výpočtový tepelný výkon směřující do vytápěného prostoru (W)
Qa - tepelná ztráta spalinami do komína (W).
Jednotlivé výkony jsou dány následujícími vztahy.
Tepelný příkon (W) daný přísunem dřeva
![]()
md je hmotnostní přísun dřeva (kg.h-1)
bd - výhřevnost dřeva (obr. 2), (Wh.kg-1)
cd - měrná tepelná kapacita dřeva (tab. 1) (Wh.kg-1.K-1)
td - teplota vstupního dřeva (°C)
tr - referenční teplota pro výhřevnost = 20 (°C).
Tepelný příkon (W) daný průtokem spalovacího vzduchu
![]()
cv je měrná tepelná kapacita vzduchu (tab. 1) (Wh.kg-1.K-1)
mv - hmotnostní přítok vzduchu (kg.h-1)
tv - teplota vstupního vzduchu (°C).
Tepelná ztráta (W) spalinami do komína
![]()
ca je měrná tepelná kapacita spalin (tab. 1) (Wh.kg-1.K-1)
ta - teplota výstupních spalin z krbu (°C).
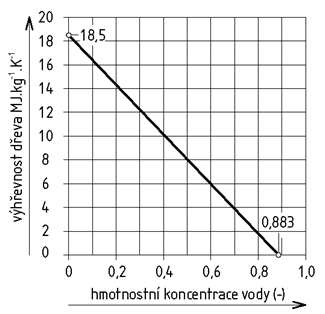
Obr. 2 - Výhřevnost dřeva
Pokud zavedeme, že teplota dřeva je shodná s teplotou vstupního vzduchu, tj. td = tv, a sloučíme vztahy (4 až 7), obdržíme po úpravách vztah pro stanovení přísunu dřeva (kg.h-1)
![]()
u je poměrná hmotnostní potřeba spalovacího vzduchu vztažená k hmotnosti dřeva dle vztahu (2)
= Mv / Md = 9,44 / 1 = 9,44 (kg.kg-1).
Když ve vztahu (8) použijeme namísto jednotek veličin s Wh jednotky s MJ obdržíme výpočtový tvar
![]()
md je hmotnostní přísun dřeva (kg.h-1)
Qn - výpočtový tepelný výkon směřující do vytápěného prostoru (kW)
bd - výhřevnost dřeva (MJ.kg-1)
cd - měrná tepelná kapacita dřeva (MJ.kg-1.K-1)
ca - měrná tepelná kapacita spalin (MJ.kg-1.K-1),
přičemž jednotky ostatních veličin jsou shodné s jednotkami předcházejících vztahů.
Vztahy potřebné pro hlavní výpočty
Hmotnostní podíl kyslíku O2 ve vzduchu (-) je dán vztahem
![]()
MO2 je hmotnost kyslíku O2 (kg)
Mv - hmotnost vzduchu (kg)
pO2 - objemový podíl kyslíku O2 ve vzduchu = 0,21 (-)
ρvO2 - hustota kyslíku O2 = 1,43 při 0 °C a 101,3 kPa (kg.m-3)
pN2 - objemový podíl dusíku N2 ve vzduchu = 0,79 (-)
ρN2 - hustota dusíku N2 = 1,25 při 0 °C a 101,3 kPa (kg.m-3).
Hmotnostní podíl dusíku N2 ve vzduchu (-) je potom dán vztahem
![]()
| Látka | Hustota ρ | Měrná tepelná kapacita c | Kinematická viskozita υ |
|---|---|---|---|
| kg.m-3 | 10-3 MJ.kg-1.K-1 | Wh.kg-1.K-1 | |
| Kyslík O2 | 1,43 | - | - |
| Dusík N2 | 1,25 | - | - |
| Vzduch | 1,29 | 1 | 0,28 |
| Oxid uhličitý CO2 | 1,98 | 1 | 0,28 |
| Vodní pára | 0,60 | - | - |
| Spaliny 1) | 1,25 | 1,08 | 0,30 |
| Dřevo 3) | - | 2,7 | 0,75 |
Tab. 1 - Vlastnosti prvků a látek potřebné pro výpočty (pro 0 °C, 101,3 kPa)
1) při hmotnostní vlhkosti dřeva 20 % a součiniteli přebytku vzduchu λ = 2,
2) při 250 °C, 3) při hmotnostní vlhkosti dřeva 20 %.
Hustotu spalin (kg.m-3) při 0 °C a 101,3 kPa lze stanovit ze vztahu, ve kterém Σ jsou od 1 do 4,
![]()
Mi je hmotnost složky "i" (kg)
ρi - hustota složky "i" při 0 °C a 101,3 kPa (tab. 1) (kg.m-3)
i - pořadí složky "i" (-).
Takže hustota spalin, které mají složky v pořadí oxid uhličitý CO2, vodní pára H2O, dusík N2 a vzduch bude
![]()
Hustotu spalin (kg.m-3) pro zvolenou teplotu stanovíme ze vztahu
![]()
ρa0 je hustota spalin při 0 °C a 101,3 kPa (kg.m-3)
ta0 - teplota spalin při 0 °C (°C)
ta - teplota spalin při zvolené teplotě (°C).
Pro výpočet součinitele tření v potrubí λ je nutné znát průměr potrubí, rychlost tekutiny, Reynoldsovo kriterium a poměrnou drsnost potrubí.
Průměr potrubí (m) je dán vztahem
![]()
V je objemový průtok tekutiny (m3.s-1)
v - rychlost tekutiny (m.s-1).
Pro rychlosti ve vzduchové i spalinové cestě se volí vv = va = 1 m.s-1.
Reynoldsovo kriterium (-) je dáno vztahem
![]()
υ je kinematická viskozita tekutiny (m2.s-1).
Poměrná drsnost potrubí (-) je dána poměrem e / d, kde e je drsnost potrubí (m). Pro vzduchospalinovou cestu se volí poměrná drsnost 0,01.
Pro rychlost ve vzduchové cestě vv = 1 m.s-1, pro průměr vzduchové cesty d = 0,2 m a pro kinematickou viskozitu vzduchu při 0 °C υv = 14.10-6 m2.s-1 bude Reynoldsovo kriterium
Re = 1 . 0,2 / (14.10-6) = 1,43.104.
Hodnotě Re = 104 a poměrné drsnosti potrubí e / d = 0,01 odpovídá ze známého diagramu λv = f (Re; e/d) součinitel tření vzduchové cesty λv = 0,045. Vzhledem k tomu, že rychlosti ve vzduchové a ve spalinové cestě se volí shodné, průměry obou cest a kinematické viskozity vzduchu i spalin jsou souměřitelné, předpokládá se, že i Re jsou souměřitelná. Potom může být součinitel tření uvažován i u spalinové cesty shodný, tj. λa = 0,045.
Hlavní výpočtové vztahy
Hmotnostní průtok vzduchu (kg.h-1)
![]()
u je poměrná hmotnostní potřeba spalovacího vzduchu vztažená k hmotnosti dřeva; u vztahu (8) (kg.kg-1)
md - hmotnostní přísun dřeva (kg.h-1).
Objemový průtok vzduchu (m3.h-1)
![]()
mv je hmotnostní průtok vzduchu (kg.h-1)
ρv - hustota vzduchu (kg.m-3).
Hmotnostní průtok spalin (kg.h-1)
![]()
a je poměrné hmotnostní množství spalin vztažené k hmotnosti dřeva, vztah (3) (kg.kg-1)
md - hmotnostní přísun dřeva (kg.h-1).
Objemový průtok spalin v komíně (m3.h-1)
![]()
ma je hmotnostní průtok spalin (kg.h-1)
ρa2 - hustota spalin v komínu (kg.m-3)
ta2 - teplota spalin v komínu (°C)
ρa0 - hustota spalin při 0 °C (kg.m-3)
ta0 - teplota spalin při 0 °C (°C).
Účinný tah krbu a komínu (Pa) (obr. 3) je dán vztahem
![]()
h je účinná výška krbu (m)
g - zemské zrychlení (m.s-2)
ρa1 - hustota spalin v krbu (kg.m-3)
ρv - hustota venkovního vzduchu (kg.m-3)
H - účinná výška komínu (m)
ρa2 - hustota spalin v komínu (kg.m-3).
Dosadíme-li vztah (14) do vztahu (21) obdržíme po úpravě vztah pro výpočet účinného tahu krbu a komínu (Pa)
![]()
Tlaková ztráta vzduchospalinové cesty (Pa) je dána vztahem, kde je zanedbána tlaková ztráta spalin v krbu, takže
![]()
Δpzv je tlaková ztráta vzduchové cesty (Pa)
Δpza - tlaková ztráta spalinové cesty (Pa)
λv - součinitel tření vzduchové cesty (-)
L - délka vzduchové cesty (m)
d - průměr vzduchové cesty (m)
ςv - součet součinitelů místních odporů vzduchové cesty (-)
vv - rychlost vzduchu ve vzduchové cestě (m.s-1)
λa - součinitel tření spalinové cesty (-)
D - průměr spalinové cesty (m)
ςa - součet součinitelů místních odporů spalinové cesty (-)
va - rychlost spalin ve spalinové cestě (m.s-1).
Příklad
Zadání
Máme navrhnout vzduchospalinovou cestu pro krb o jmenovitém tepelném výkonu Qn = 10 kW. V krbu bude spalováno dřevo s poměrnou hmotnostní vlhkostí 0,2, o výhřevnosti bd = 14,3 MJ.kg-1 a o teplotě td = -12 °C. Spalování probíhá se součinitelem přebytku vzduchu λ = 2. Délka vzduchové cesty L = 2 m, součet součinitelů místních odporů ve vzduchové cestě ςv = 2, poměrná drsnost vzduchové cesty e / d = 0,01. Výška krbu je h = 1 m, účinná výška komínu H = 5 m, součet součinitelů místních odporů ve spalinové cestě ςa = 2, poměrná drsnost spalinové cesty e / D = 0,01. Teplota vstupního vzduchu je tv = 0 °C, teplota spalin v krbu ta1 = 500 °C, teplota spalin v komínu ta2 = 250 °C. Součinitel tření vzduchospalinové cesty λv = λa = 0,045. Hustoty a měrné tepelné kapacity prvků a látek potřebné pro výpočty jsou uvedeny v tab. 1.
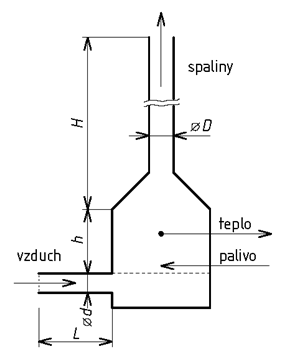
Obr. 3 - Schema krbu
Řešení
Přísun dřeva je dán vztahem (9)
md = 3,6 . 10 / {14,3 + (1 + 9,44) . [2,7.10-3 . (-12 - 20) - 1,08.10-3 . (250 - 20)]} = 3,33 kg.h-1.
Hmotnostní průtok vzduchu je dán vztahem (17)
mv = u . md = 9,44 . 3,33 = 31,44 kg.h-1.
Objemový průtok vzduchu je dán vztahem (18)
Vv = 31,44 / 1,29 = 24,37 m3.h-1 = 6,77.10-3 m3.s-1.
Průměr vzduchové cesty je dán vztahem (15)
d = [4 . 6,77.10-3 / (π . 1]0,5 = 0,093 m.
Hmotnostní průtok spalin je dán vztahem (19)
ma = a . md = 10,44 . 3,33 = 34,77 kg.h-1.
Objemový průtok spalin je dán vztahem (20)
Va = 34,77 . (250 + 273) / [1,25 . (0 + 273)] = 53,29 m3.h-1 = 14,80.10-3 m3.s-1.
Průměr spalinové cesty je dán vztahem (15)
D = [4 . 14,80.10-3 / (π . 1]0,5 = 0,14 m.
Účinný tah krbu a komínu je dán vztahem (22)
Δpt = 9,81 . 1,29 . (1 + 5) - 9,81 . 1,25 . (0 + 273) . [1 / (500 + 273) + 5 / (250 + 273)] = 39,6 Pa.
Tlaková ztráta vzduchospalinové cesty je dána vztahem (23)
Δpz = 0,5 . {(0,045 . 2 / 0,093 + 2) . 12 . 1,29 + (0,045 . 5 / 0,14 + 2) . 12 . 1,25} = 4,2 Pa.
Komentář k praktickému příkladu
Protože tlaková ztráta vzduchospalinové cesty Δpz = 4,2 Pa je menší než účinný tah krbu a komínu Δpt = 39,6 Pa, lze považovat dimenze vzduchospalinové cesty za dostatečné pro provoz krbu. Větší účinný tah krbu a komínu není na závadu, neboť po naložení paliva do krbu se zvyšuje výkon a vzduchospalinová cesta tomu nebrání. Také je možné zaokrouhlit průměr vzduchové cesty na 0,1 m a spalinové cesty na 0,15 m.
Popsaný výpočet je poměrně složitý, a proto byl po dohodě s autorem zpracován do formy on-line výpočetní pomůcky Návrh vzduchospalinové cesty pro krb. Tento článek je tak současně i nápovědou.
Výsledek výpočtu, který je založen na přírodních zákonech, je nutné před praktickým využitím porovnat i s požadavky norem, které se vztahují k problematice vzduchospalinových cest.
Použitá literatura:
Kolektiv, Topenářská příručka, svazek 2, Gas Říčany, 2001
Recenze článku Ing. Vladimíra Valenty "Dimenzování vzduchospalinových cest krbů"
Recenzent: Doc. Ing. Karel Papež, CSc
V poslední době se v řadě rodinných domů vyskytují krby v různém provedení jako doplněk vybavení domu hlavně po stránce estetické a v některých případech jako prvek, kterým můžeme občasně zlepšit tepelné mikroklima ústředních prostor domu.
V řadě případů není zvládnuta problematika spalování paliva z důvodů naprosté neznalosti souvislostí se spalováním paliva. Pro dokonalé spalování je především nutno přivést dostatečné množství vzduchu nutného pro spalování a hoření. Kromě toho je nutné, aby byla správně nadimenzovaná i spalinová cesta – komín. Uvedený článek tuto problematiku komplexně řeší. Pro čtenáře je instruktivní i příklad, který nám ukazuje řadu souvislostí, které pak vedou ke správnému nadimenzování vzduchospalinové cesty.
Článek považuji za velký přínos, který pomůže v praktických případech odstranit případné potíže v této oblasti.
The paper focuses on the sizing of chimneys for fireplaces in which wood is burnt. Before the dimensioning itself the combustion equation and the derived equations for determining the flow of fire-wood and the flow of combustion air and gas are listed. At the end, the paper provides an example of calculation.
