Výpočet napjatosti ohýbaných nosných prvků z vrstveného skla v závislosti na tuhosti folie PVB a EVA
Ohýbané nosné konstrukce z vrstveného skla jsou v dnešním stavitelství navrhovány stále častěji, a to především kvůli své zbytkové únosnosti v nehodové situaci. Dojde-li v běžném provozu k poškození jedné tabule v souvrství, zbylé tabule jsou stále schopny přenášet část užitného zatížení. V případech, kdy je při návrhu uvažována smyková tuhost polymerní folie, je stanovení napjatosti a průhybů těchto prvků značně komplikované. Smyková tuhost folie závisí především na okolní teplotě a délce trvání statického zatížení. V současnosti nejsou k dispozici jednotné evropské normy pro návrh ohýbaných konstrukcí z vrstveného skla, které by zohledňovaly pozitivní vliv smykové tuhosti polymerní folie. Tento článek je zaměřen na výpočet napjatosti a průhybů ohýbané po obvodě prostě podepřené čtvercové desky z vrstveného skla zatížené rovnoměrným krátkodobým zatížením, který zohledňuje experimentálně stanovenou smykovou tuhost běžných polymerních folií PVB (Trosifol BG-R-20, Trosifol ExtraStrong) a EVA (Evasafe).
1. Úvod
Stavební inženýři v současnosti navrhují ohýbané prvky z vrstveného skla bez ohledu na pozitivní vliv smykové tuhosti polymerní folie, tedy na straně bezpečné. Tento přístup, který je v souladu s německou normou DIN 18008 [1], vede k nákladným a neekonomickým konstrukcím. Stanovení napjatosti a průhybů ohýbaných prvků z vrstveného skla je v případech, kdy je uvažována smyková tuhost polymerní folie, značně komplikované. Je možné použít pracovní verzi evropských přednorem [2–3], k dispozici jsou také analytické metody, např. metoda Wölfel-Bennison, Metoda efektivní tloušťky nebo Metoda sečné tuhosti. Tyto metody se řadí mezi metody variační a spočívají v nalezení vhodné aproximace odezvy ohýbaných nosníků a desek z vrstveného skla pomocí vhodných průhybových funkcí minimalizujících funkcionál deformační energie. Podrobnosti a přesnost těchto výpočetních metod lze nalézt v [4] a [5]. Napjatost a deformace prvků z vrstveného skla je také možné stanovit na základě numerického modelu metodou konečných prvků např. v programech ANSYS®, RFEM® nebo ABAQUS®. Tyto modely vyžadují správný typ okrajových podmínek, známou tuhost polymerní folie a výstižně zvolenou síť konečných prvků. Numerické modelování je časově náročné, jsou-li však vstupní parametry dostatečně výstižné, lze očekávat téměř přesné výsledky. V Kloknerově ústavu ČVUT byla provedena série smykových statických zatěžovacích zkoušek běžně používaných PVB folií (Trosifol®, Trosifol Extra Strong®) a folie EVA (Evasafe®). Výsledky závislosti počáteční smykové tuhosti těchto folií na okolní teplotě a rychlosti zatížení byly publikovány v [6]. Hodnoty těchto smykových tuhostí budou v tomto příspěvku brány jako vstupní parametry pro numerický model čtvercové po obvodě prostě podepřené desky z vrstveného skla zatížené rovnoměrným krátkodobým zatížením. Cílem tohoto textu je ukázat rozdíl v analytickém výpočtu zvolené desky dle platné normy DIN 18008, která spolupůsobení jednotlivých tabulí v souvrství zanedbává a ve výpočtu této desky pomocí numerického modelu, který toto spolupůsobení vystihuje.
2. Experimentální část
Pro vyloučení časového vlivu na smykovou tuhost zkoušené folie byly statické zkoušky provedeny jako krátkodobé. Na Obr. 1 jsou zobrazeny obecné závislosti smykového napětí τ na smykové deformaci folie γ pro různé teploty T zjištěné na základě experimentů. Křivky jsou nelineární a závislé na okolní teplotě. Okamžitá smyková tuhost folie G není konstantní, ale závisí na hodnotě její smykové deformace. Počáteční smykové moduly zkoušených folií byly stanoveny pomocí postupu zobrazeného na Obr. 1, kde průnik kružnice o poloměru 0,4 MPa s odpovídající křivkou vytyčuje bod, pomocí kterého byla vypočtena hodnota počátečního smykového modulu folie G. Tento počáteční modul je sečný a je stanoven na bezpečné straně s ohledem na hodnoty jemu odpovídajících smykových deformací folie tak, aby tyto deformace byly větší než 1 %. Tak vysoké hodnoty smykových deformací se v běžných ohýbaných prvcích z vrstveného skla nevyskytují [7]. Tab. 1 shrnuje průměrné hodnoty experimentálně zjištěných počátečních smykových modulů tuhosti G pro zkoušené folie. Hodnoty ukazují, že zvýšení teploty má pro tyto folie za následek snížení hodnoty smykového modulu. Tyto hodnoty lze použít do numerických modelů, avšak pouze za předpokladu, že zatížení působí krátkodobě. Při dlouhodobém působení zatížení se začnou projevovat vizkoelastické vlastnosti folií a hodnoty těchto modulů se začnou v čase postupně snižovat [8]. Přesný popis, provedení experimentů a shrnutí důležitých výsledků lze nalézt v [6].
| Teplota [°C] | PVB G [MPa] | PVB ES G [MPa] | EVA S G [MPa] |
|---|---|---|---|
| 0 °C; 2,0 mm/min | 144,13 | 1887,94 | 13,26 |
| 0 °C; 0,5 mm/min | 103,31 | 13,28 | |
| 20 °C; 2,0 mm/min | 1,7 | 225,46 | 6,86 |
| 20 °C; 0,5 mm/min | 1,09 | 105,22 | 6,39 |
| 20 °C; 0,125 mm/min | 0,79 | 61,3 | 6,22 |
| 40 °C; 2,0 mm/min | 0,46 | 0,9 | 3,43 |
| 40 °C; 0,5 mm/min | 0,44 | neurčeno | neurčeno |
| 40 °C; 0,125 mm/min | 0,31 | 0,6 | 3,09 |
| 60 °C; 2,0 mm/min | 0,25 | 0,46 | 1,64 |
| 60 °C; 0,5 mm/min | 0,14 | neurčeno | neurčeno |
| 60 °C; 0,125 mm/min | 0,11 | 0,37 | 1,44 |
3. Parametry řešené desky, model
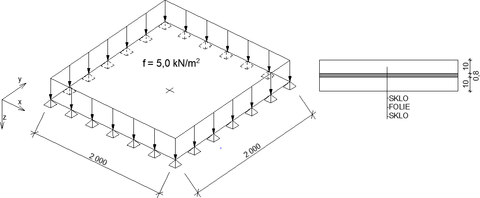
Pro porovnání výsledků zjednodušeného analytického výpočtu a numerického modelu je uvažována po obvodě prostě podepřená čtvercová deska z dvojvrstvého skla o rozměrech 2000 × 2000 mm, viz Obr. 2. Podepření je uvažováno na spodních vláknech spodní tabule a zajišťuje nulové posuny podepřených hran ve směrech os x, y a z. Tloušťka vrstev skla je zvolena shodně 10 mm, tloušťka folie mezivrstvy je zvolena 0,8 mm. Deska je zatížená kolmo na svoji rovinu svislým krátkodobým rovnoměrným zatížením 5,0 kN/m2 za okolní teploty 0, 20, 40 a 60 °C.
3.1. Zjednodušený analytický výpočet dle DIN 18008
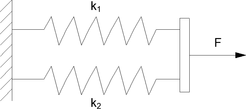
Norma DIN 18008 je v současnosti jedním z mála předpisů, které lze použít pro návrh ohýbaných konstrukcí z vrstveného skla zatížených kolmo na svoji rovinu. Smykové spolupůsobení jednotlivých tabulí v souvrství pomocí polymerní folie se však zanedbává, tudíž se jedná o časově nenáročný a velmi zjednodušený analytický výpočet. Zatížení se rozděluje mezi jednotlivé vrstvy v souvrství podle jejich deskových tuhostí, což si lze představit paralelně spojenými pružinami o tuhosti k zatíženými celkovou silou F, viz Obr. 3. Pružina s nejnižší hodnotou tuhosti přenáší nejmenší sílu a naopak. Pro řešenou desku to znamená, že každá tabule v souvrství přenáší zatížení 2,5 kN/m2 a může být posuzována samostatně. Tento přístup vede k bezpečnému, ale v určitých případech k příliš konzervativnímu návrhu prvků z vrstveného skla.
Vzhledem ke zvolené geometrii desky bude z hlediska napjatosti rozhodující bod uprostřed jejího rozpětí, který je na Obr. 2 označen křížkem. V tomto bodě jsou navíc hodnoty hlavních napětí rovny hodnotám normálových napětí ve směru os x a y. Pro ilustraci náročnosti zde uvádíme postup tohoto analytického výpočtu dle [9] pro řešenou desku. Výpočet bude proveden v jednotkách [N, mm, MPa]. Pro výpočet normálových napětí je nejprve potřeba stanovit součinitele roznosu zatížení v příčných směrech x a y z odpovídajících grafů v [9]. Deska je čtvercová, tudíž je hodnota těchto součinitelů shodná ηx = ηy = 0,046. Měrný ohybový moment pro celé souvrství uprostřed rozpětí se stanoví jako
kde a a b jsou půdorysné rozměry desky a f je rovnoměrné zatížení. Při zanedbání smykové tuhosti folie se měrný ohybový moment pro celé souvrství rozdělí mezi jednotlivé vrstvy v poměru jejich deskových tuhostí K podle rovnice 2 jako
kde ti je tloušťka jedné tabule. Vzhledem k tomu, že jsou tloušťky obou tabulí v souvrství shodné, bude shodné i namáhání obou tabulí. Posouzení bude tedy provedeno pouze pro jednu tabuli v souvrství. Měrný ohybový moment pro jednu tabuli uprostřed rozpětí se stanoví dle rovnice 3
Měrný průřezový modul jedné tabule se vypočte podle rovnice 4 a normálové napětí uprostřed rozpětí desky podle rovnice 5
Při stanovení průhybů je postup obdobný. Celé souvrství je převedeno na desku s odpovídající efektivní tloušťkou t*, která dosahuje stejných průhybů jako celé souvrství. Nejprve je nutné z odpovídajících grafů dle [9] stanovit součinitel roznosu příčného zatížení ηf pro výpočet průhybu. Pro čtvercovou desku je tento součinitel ηf = 0,004. Efektivní tloušťka monolitické desky t* se vypočte podle rovnice 6 a desková tuhost K desky efektivní tloušťky se vypočte podle rovnice 7
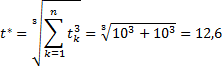 (6)
[mm]
(6)
[mm]
kde Youngův modul pružnosti skla E = 70 GPa a Poissonovo číslo skla ν = 0,23. Podle rovnice 8 je průhyb skleněné desky efektivní tloušťky t* roven 26,0 mm.
3.2 Numerický model
Základní myšlenka výpočtu napjatosti a průhybů desky pomocí numerického modelu spočívá v nalezení vhodné aproximace pole posunutí pomocí interpolačních funkcí minimalizujících funkcionál deformační energie (Lagrangeova podmínka minima). Více o metodě konečných prvků (MKP) lze nalézt např. v [10]. Numerický model řešené desky byl vytvořen v software Dlubal RFEM 4-RF Glass. Sklo bylo uvažováno jako izotropní lineárně elastický materiál s modulem pružnosti 70 GPa a Poissonovým číslem 0,23. Folie byla v modelech rovněž uvažována jako izotropní materiál s Poissonovým číslem 0,45 [3] a modulem tuhosti ve smyku G stanoveným experimentálně pro rychlost zatěžování 0,5 mm/min (pro teplotu 0 °C) a 0,125 mm/min (pro teploty 20 až 60 °C), viz Tab. 1. Jako základní prvek sítě byl zvolen osmiuzlový 3D SOLID, kde každému uzlu byly přiřazeny 3 stupně volnosti. Základní délka kroku sítě byla 40 mm, hrana desky byla tedy složena z padesáti prvků. Vrstva skla byla na výšku tvořena dvěma prvky, folie tvořící mezivrstvu mezi tabulemi skla pak byla tvořena jedním prvkem. Tvar zvolené sítě v půdorysu desky a po výšce souvrství je zobrazen na Obr. 4. Úloha byla řešena I. řádem s konstantní maticí tuhosti. U tohoto typu deskových konstrukcí, kde podélné rozměry několikanásobně převyšují tloušťku skla, může docházet k průhybům generujícím membránovou napjatost. Umožňuje-li použitý software nelineární výpočet zohledňující velké deformace, je vhodné tento výpočet použít i za cenu jeho větší časové náročnosti. Výsledkem jsou nižší hodnoty vypočtených průhybů a přesnější rozložení napjatosti [11]. Pro zde řešenou čtvercovou desku jsou rozdíly výsledků nepatrné.
4. Obdržené výsledky, diskuse
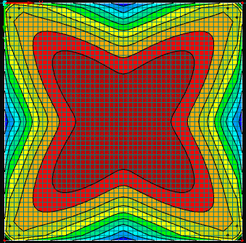
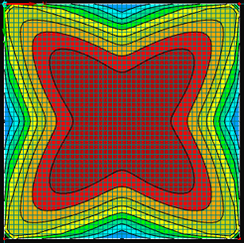
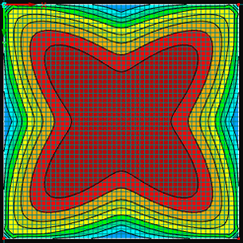
V následujícím textu budou porovnány výsledky získané pomocí zjednodušeného analytického výpočtu dle DIN 18008 [1] s výsledky z numerického modelu v RFEM. Použitá folie Trosifol je v následujícím textu označena jako PVB, Trosifol Extra Strong je označena jako PVB ES a folie Evasafe je označena jako EVA S. Na Obr. 5 je vidět rozložení rozhodujících hlavních napětí pro spodní vlákna spodní tabule v numerickém modelu pro tabuli zatíženou při teplotě 40 °C. Ze všech tří folií vykazuje folie EVA S nejvyšší hodnotu počáteční smykové tuhosti – 3,09 MPa, což má za následek nejnižší hodnoty hlavních tahových napětí uprostřed rozpětí řešené desky, a to 15,7 MPa. Naopak folie PVB dosahuje při teplotě 40 °C nejnižší hodnoty tohoto modulu – pouze 0,31 MPa. To znamená, že souvrství s touto folií dosahuje uprostřed rozpětí nejvyšších hodnot hlavních tahových napětí 21,6 MPa. Rovněž ohybová tuhost souvrství s PVB folií je při teplotě 40 °C nejnižší, což vede zároveň k nejvyšším hodnotám vypočteného svislého průhybu desky 16,2 mm. Souvrství s folií EVA S má naopak nejvyšší ohybovou tuhost a dosahuje nejmenších hodnot svislého průhybu 8,5 mm. Pro srovnání připomínáme hodnoty největších hlavních tahových napětí 27,5 MPa a průhybů 26 mm ze zjednodušeného analytického výpočtu.
Obr. 5 Rozložení rozhodujících hlavních napětí v [MPa] u spodních vláken spodní tabule pro testované folie při teplotě 40 °C
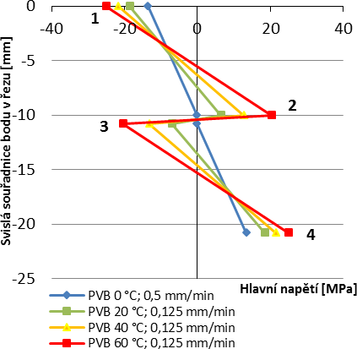
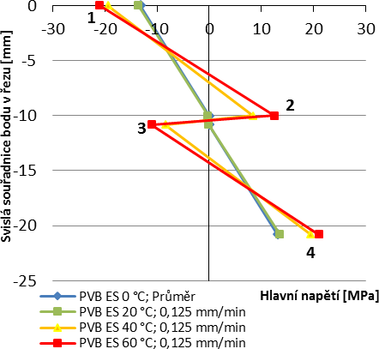
Obr. 6 zobrazuje vývoj rozhodujícího hlavního napětí uprostřed rozpětí desky při zvyšující se teplotě pro souvrství s foliemi PVB a PVB ES, které byly získány z numerického modelu. Oba grafy ukazují, že při zvýšení teploty dochází k nárůstu hlavních napětí po průřezu desky. Pro posouzení únosnosti konstrukce rozhoduje napětí u spodních vláken spodní tabule (bod 4). Pro souvrství s folií PVB rostou hlavní napětí rovnoměrně, v bodě 4 je jejich rozdíl mezi teplotami 0 °C a 60 °C roven 11,6 MPa. Pro souvrství s folií PVB ES dochází k výraznému nárůstu hlavních napětí mezi teplotami 20 °C a 40 °C, což je způsobeno prudkým poklesem smykové tuhosti této folie mezi těmito teplotami, viz Tab. 1. Porovnáme-li na Obr. 6 velikosti hlavních napětí v bodě 4 pro obě folie při stejných teplotách, vyjde najevo, že souvrství s folií PVB ES dosahuje nižších hodnot těchto napětí. Největší rozdíl činí 5 MPa při teplotě 20 °C. Přestože jsou obě folie vyrobeny z polyvinylbutyralu, vykazují odlišnou tuhost ve smyku, což má za následek různý průběh hlavních napětí po průřezu. Pro jednoznačnou identifikaci materiálu tedy nestačí označení chemického složení použité folie (např. označení pouze PVB), ale je třeba doplnit obchodní název a materiálový list.
Obr. 6 Vývoj hlavních napětí uprostřed rozpětí desky při zvyšující se teplotě pro folie PVB a PVB ES obdržený z numerického modelu, bod 1 = horní vlákna horní tabule, bod 2 = spodní vlákna horní tabule, bod 3 = horní vlákna spodní tabule, bod 4 = spodní vlákna spodní tabule
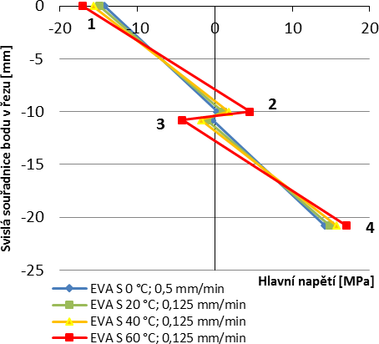
Grafy na Obr. 7 zobrazují vývoj hlavních napětí uprostřed rozpětí desky pro souvrství s folií EVA S při nárůstu teploty a také rozložení těchto napětí po průřezu v případě, že je smykové spolupůsobení vrstev zanedbáno (výpočet dle DIN 18008). Pro folii EVA S nedochází mezi jednotlivými teplotami ke skokovému nárůstu hlavních napětí, což je způsobeno postupným snižováním její smykové tuhosti, viz Tab. 1. Folie EVA S zajišťuje v porovnání s PVB foliemi spolupůsobení tabulí v souvrství i při teplotách 40 °C a 60 °C. Použití této folie při vyšších teplotách je tedy vhodné. Zanedbáme-li smykové spolupůsobení jednotlivých vrstev, obdržíme v bodě 4 velikost hlavního napětí 27,5 MPa. Při teplotě 0 °C bychom ve srovnání s numerickým modelem pro souvrství s PVB folií analyticky vypočetli napětí o 14,1 MPa vyšší, pro souvrství s folií PVB ES o 14,4 MPa vyšší a pro souvrství s folií EVA S o 13,3 MPa vyšší. Zjednodušený analytický výpočet by tedy byl v tomto případě velmi konzervativní. Pro teplotu 60 °C je nejvýraznější rozdíl v analyticky a numericky získaných napětích pro folii EVA S 10,5 MPa, naopak pro folii PVB je tento rozdíl pouze 2,5 MPa.
Obr. 7 Vývoj hlavních napětí uprostřed rozpětí desky při zvyšující se teplotě pro folii EVA S z numerického modelu, hodnoty získané z analytického výpočtu [1], bod 1 = horní vlákna horní tabule, bod 2 = spodní vlákna horní tabule, bod 3 = horní vlákna spodní tabule, bod 4 = spodní vlákna spodní tabule
Graf na Obr. 8 zobrazuje nárůst průhybů uprostřed rozpětí desky při zvyšující se teplotě pro zkoušené folie a porovnání těchto průhybů s analytickým výpočtem. Z grafu je patrné, že nejvýraznějšího nárůstu průhybu je dosaženo pro souvrství s folií PVB, a to o 14,6 mm mezi teplotami 0 °C a 60 °C. Naopak pro souvrství s folií EVA S není nárůst průhybu mezi krajními teplotami tak výrazný – pouze 3,3 mm. Velikost smykového modulu 1,44 MPa folie EVA S při 60 °C zajišťuje v porovnání se smykovými moduly obou PVB folií vyšší ohybovou tuhost celého souvrství a dosažení nejnižších průhybů. Při zanedbání smykového spolupůsobení desek v souvrství bychom v porovnání s numerickým modelem při teplotě 0 °C vypočetli analyticky svislý průhyb v průměru o 19,6 mm vyšší. Rozdíl mezi analyticky a numericky vypočtenými průhyby se při zvyšující se teplotě pro jednotlivé folie postupně snižuje. Při teplotě 60 °C je pro souvrství s folií PVB tento rozdíl pouze 5,2 mm, pro souvrství s folií PVB ES je rozdíl 10,5 mm a pro souvrství s folií EVA S je rozdíl 15,8 mm.
V Tab. 2 až 4 jsou uvedeny číselné hodnoty analyticky a numericky vypočtených hlavních napětí σ1 a průhybů w dolních vláken dolní tabule uprostřed rozpětí (bod č. 4) včetně jejich rozdílů při všech zkoumaných teplotách pro řešené folie. Zanedbáním smykového spolupůsobení jednotlivých tabulí v souvrství bychom pro rovnoměrné krátkodobé zatížení dostali hodnoty na bezpečné straně, zjednodušený analytický výpočet je však zejména pro nižší teploty (0 a 20 °C) konzervativní. Z praktického hlediska je vhodné při známých tuhostech folií pro krátkodobé zatížení zohlednit smykové spolupůsobení jednotlivých tabulí v souvrství a navrhnout tak hospodárnější konstrukci. Je nutné si uvědomit, že smykové moduly tuhosti ze statických smykových zkoušek polymerních folií podávají informaci o počáteční tuhosti folie. Pro dlouhotrvající statické zatížení, kde se projevují její vizkoelastické vlastnosti, je nutné provést dynamické smykové zkoušky [12] a zjistit tak vývoj smykového modulu tuhosti folie v čase. Při dlouhotrvajícím statickém zatížení totiž pro většinu folií hodnota tohoto modulu v čase klesá. Není-li tuhost folie prokázána statickými, ani dynamickými smykovými zkouškami, je bezpečné ji při návrhu konstrukce raději zanedbat a použít zjednodušený analytický výpočet.
| T [°C] | σ1,num. [MPa] | σ1,anal. [MPa] | σ1,anal. − σ1,num. [MPa] | wnum. [mm] | wanal. [mm] | wanal. − wnum. [mm] |
|---|---|---|---|---|---|---|
| 0 | 13,4 | 27,5 | 14,1 | 6,2 | 26,0 | 19,8 |
| 20 | 18,6 | 27,5 | 8,9 | 12,2 | 26,0 | 13,8 |
| 40 | 21,6 | 27,5 | 5,9 | 16,2 | 26,0 | 9,8 |
| 60 | 25,0 | 27,5 | 2,5 | 20,8 | 26,0 | 5,2 |
| T [°C] | σ1,num. [MPa] | σ1,anal. [MPa] | σ1,anal. − σ1,num. [MPa] | wnum. [mm] | wanal. [mm] | wanal. − wnum. [mm] |
|---|---|---|---|---|---|---|
| 0 | 13,1 | 27,5 | 14,4 | 5,9 | 26,0 | 20,1 |
| 20 | 13,6 | 27,5 | 13,9 | 6,2 | 26,0 | 19,8 |
| 40 | 19,5 | 27,5 | 8,1 | 13,4 | 26,0 | 12,6 |
| 60 | 21,0 | 27,5 | 6,5 | 15,5 | 26,0 | 10,5 |
| T [°C] | σ1,num. [MPa] | σ1,anal. [MPa] | σ1,anal. − σ1,num. [MPa] | wnum. [mm] | wanal. [mm] | wanal. − wnum. [mm] |
|---|---|---|---|---|---|---|
| 0 | 14,2 | 27,5 | 13,3 | 6,9 | 26,0 | 19,1 |
| 20 | 14,86 | 27,5 | 12,64 | 7,5 | 26,0 | 18,5 |
| 40 | 15,7 | 27,5 | 11,8 | 8,5 | 26,0 | 17,5 |
| 60 | 17 | 27,5 | 10,5 | 10,2 | 26,0 | 15,8 |
5. Závěr
Tento text ukázal vliv počáteční smykové tuhosti polymerních folií PVB (Trosifol®), PVB ES (Trosifol ExtraStrong®) a EVA S (Evasafe®) na velikost průhybů a přerozdělení hlavních napětí po průřezu po obvodě prostě podepřené čtvercové tabule z dvouvrstvého skla zatížené krátkodobým rovnoměrným zatížením při teplotách 0, 20, 40 a 60 °C. Publikované výsledky byly získané z numerického MKP modelu v software Dlubal RFEM 4, modul RF Glass. Sklo i folie byly uvažovány v modelu jako izotropní materiály. Smykové tuhosti těchto folií do numerického modelu byly získány na základě statických zatěžovacích zkoušek provedených v Kloknerově ústavu ČVUT [6]. Obdržené výsledky byly porovnány se zjednodušeným analytickým výpočtem podle platné normy DIN 18008 [1]. Bylo zjištěno, že při zanedbání smykového spolupůsobení jednotlivých tabulí v souvrství (analytický výpočet) jsou získané výsledky na bezpečné straně, ale pro většinu případů jsou zároveň příliš konzervativní. Numerický výpočet s experimentálně ověřenými tuhostmi folií tedy poskytuje příznivější výsledky a umožňuje hospodárnější návrh ohýbané konstrukce z vrstveného skla, vyžaduje však správné zavedení okrajových podmínek, materiálových parametrů a výstižně zvolenou síť konečných prvků. Příspěvek ukazuje zpřesnění obdržených výsledků právě pomocí numerického modelování za pomoci experimentálně ověřených smykových tuhostí polymerních folií PVB a EVA v porovnání se zjednodušeným analytickým výpočtem. Jestliže není k dispozici numerický model, ale je známa tuhost použité folie ve smyku, je možné použít další analytické metody jako např. Wölfel Bennison, Metoda efektivní tloušťky apod., které tuto tuhost ve výpočtu zohledňují a umožňují tak hospodárnější návrh ohýbaných konstrukcí z vrstveného skla. Není-li smyková tuhost folie v závislosti na teplotě a délce trvání zatížení experimentálně stanovena, je bezpečné ji při návrhu těchto konstrukcí raději zanedbat. V běžném provozním stádiu se na desce z vrstveného skla může vyskytovat více zatěžovacích stavů s různou délkou trvání (vlastní tíha + proměnné zatížení). V takovém případě je možné desku posoudit s uvážením různých smykových modulů tuhosti vázaných k jednotlivým zatěžovacím stavům a jejich účinky sečíst, jelikož se běžně používané polymerní folie řadí mezi vizkoelastické materiály s platností superpozice účinků [12]. Tato skutečnost však dosud nebyla zahrnuta do platných norem pro návrh ohýbaných konstrukcí z vrstveného skla.
Poděkování
Tento výzkum je podporován grantem GA 16-17461 S of the Czech Science Foundation.
Reference
- DIN 18008: Glas im Bauwesen – Bemessungs und Konstruktionsregeln: Teil 1-6, DIN Deutsches Institut für Normung e.V., Berlin
- prEN 16612: Glass in building – Determination of the load resistance of glass panes by calculation and testing, CEN 2013
- prEN 16613: Laminated glass and laminated safety glass – Determination of interlayer mechanical properties, CEN 2013
- Galuppi L., Manara G. and Royer-Carfagni G. Practical expressions for the design of laminated glass, Elsevier Ltd. DOI: 10.1016/j.compositesb.2012.09.073, 2012
- Galuppi L. and Royer-Carfagni G. Effective thickness of laminated glass beams: New expression via a variational approach, Engineering Structures, 2012, vol. 38, pp 53–67
- Hána T., Eliášová M., Machalická K. a Vokáč M.: Stanovení smykového modulu folií PVB a EVA v závislosti na teplotě a rychlosti zatížení, TZB-info, 2018
- Kuntsche J., Schuster M., Schneider J. a Langer, S.: Viscoelastic Properties of Laminated Glass Interlayers –Theory and Experiments. Glass Performance Days, 143–147 (2015)
- Ferry J. D.: Viscoelastic properties of polymers, New York (1980), ISBN 04-710-4894-1
- Weller B., Engelmann M., Nicklisch F. a Weimar T.: Glasbau-Praxis, Konstruktion und Bemessung. Band 2. 3. Aufl. Berlin: Beuth Bauwerk. ISBN 9783410221975, 2012
- Bittnar Z.: Metody numerické analýzy konstrukcí, Vydavatelství ČVUT, 1983
- Molnár G., Vigh L. G., Stocker G. A Dunai L.: Finite element analysis of laminated glass plates with PVB interlayer, R periodica polytechnica, doi 10.3311/pp.ci.2012-1.04, 2012
- Lakes R.: Viscoelastic materials, New York, ISBN 05-218-8568-X, 2009
![Obr. 1 Způsob vyhodnocení počátečního smykového modulu folií pro teploty T₁ > T₂ > T₃ [6]](/docu/clanky/0178/017868o2.png)


![Obr. 7b Vývoj hlavních napětí uprostřed rozpětí desky při zvyšující se teplotě pro folii EVA S, hodnoty získané z analytického výpočtu [1], bod 1 = horní vlákna horní tabule, bod 2 = spodní vlákna horní tabule, bod 3 = horní vlákna spodní tabule, bod 4 = spodní vlákna spodní tabule](/docu/clanky/0178/017868o38.png)
![Obr. 8 Průhyb desky uprostřed rozpětí v závislosti na teplotě, porovnání s analytickým výpočtem [1]](/docu/clanky/0178/017868o40.png)