Nastavovací plátový spoj s hmoždíky a kolíky
Plátový spoj je velmi často používán při rekonstrukcích historických konstrukcí. V literatuře se většinou dočteme o konstrukčních zásadách, ale o statickém působení toho příliš mnoho nevíme. Článek nabízí výsledky experimentálních zkoušek a výpočtů MKP, na jejichž základě bylo sestaveno několik výpočetních programů vycházejících z teoretických modelů. Z výsledků je možné vyvodit závěry, které pomohou při návrhu daného spoje.
1. Úvod
Plátový spoj je velmi často používán při rekonstrukcích historických konstrukcí. Při volbě tvaru spoje, typu a množství spojovacích prostředků je nutná znalost jeho chování. V literatuře se většinou dočteme o konstrukčních zásadách, ale o statickém působení se toho moc neví. Při tvorbě nastavovacího plátu jdou proti sobě různá hlediska. Například pracnost a přesnost spoje, jeho délka, historické hledisko a statické působení. Mnohdy jdou dané pohledy proti sobě a je nutné hledat kompromis.
V minulých letech bylo v rámci projektu NAKI DF12P01OVVOO4 uděláno mnoho experimentálních zkoušek, výpočtů MKP a bylo sestaveno několik výpočetních programů vycházejících z teoretických modelů. Z výsledků je možné udělat závěry, které pomůžou při návrhu daného spoje.
2. Plátový spoj
Je-li spolehlivost dřevěné konstrukce snížena [1], je nutné přistoupit k opravě. Pokud se jedná o opravu v historických konstrukcích, je nutné zachovat co nejvíce původního materiálu. K tomu se hodí nastavovací plátový spoj [2] viz obr. 1.
Typický spoj v několika variantách je vykreslen na obr. 2. Podle provedení jsou pláty rovnočelné nebo šikmočelné. Může být i plát s vnitřním čepem, kde na jedné části je středový čep a na druhé dva pláty. Dle použitých spojovacích prostředků jsou pláty zajištěny dřevěnými kolíky, ocelovými svorníky, hmoždíky nebo jejich kombinací.
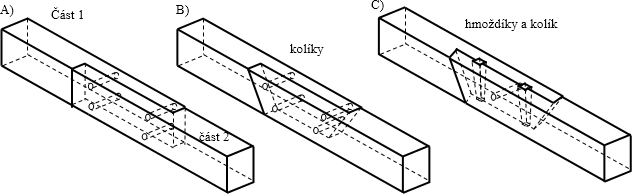
Obr. 2 a) rovnočelný plát s kolíky, b) šikmočelný plát s kolíky, c) šikmočelný plát podkosený s hmoždíky a kolíkem
3. Statické působení
Pro jednoduché využití v praxi je důležitým momentem možnost zjednodušení prostorového působení na jednodušší problém. V plátu totiž i při svislém zatížení vznikají excentrické síly, které vyvozují i ohybový moment, který konstrukci ohýbá kolmo k rovině zatížení. Zároveň vyvozují i kroutící moment v oblasti plátu. Pokud je zabráněno pohybu konstrukce kolmo k rovině zatížení je možné konstrukci zjednodušit na 2D problém. To je splněno například u stropních trámů a krokví, které jsou drženy záklopem laťováním ev. podhledem. U vazných trámů krovu většinou pomáhá konstrukci stabilizovat tahová normálová síla.
Při návrhu plátu je možné vyjít z konstrukčních zásad [2], z výpočtu pomocí metody konečných prvků [3], ze zjednodušeného teoretického modelu [4–6], nebo z experimentů [7–9].
Rovnočelný plát
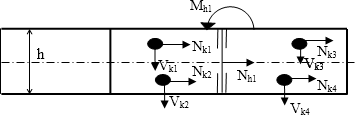
Obr. 3 Síly, které se podílí na přenášení zatížení
Tento plát je výrobně jednoduchý, protože není nutné přesné sesazení dosedacích ploch. Staticky je ale méně vhodný než plát šikmočelný. Veškeré zatížení je přenášeno pouze spojovacími prostředky viz obr. 3. V kolících působí síla, kterou si nahradíme dvěma složkami Nki, Vki. V hmoždíku působí ohybový moment Mhi a normálová síla Nhi Daný statický systém je staticky neurčitý, kde stupeň neurčitosti závisí na počtu spojovacích prostředků.
Šikmočelný plát
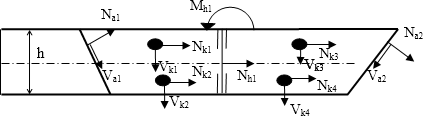
Obr. 4 Síly, které se podílí na přenášení zatížení
Při výrobě je nutné zajistit dosednutí šikmých ploch na sebe, tak aby se zapojily do statického působení. Veškeré zatížení je přenášeno čely a spojovacími prostředky viz obr. 4. K silám ve spojovacích prostředcích přibývá na čelech normálová síla Na, která vyvozuje třecí sílu Va. Rozdělení sil mezi čelo a kolíky resp. hmoždíky závisí na mnoha faktorech – více v [3–5]. Z uvedeného vyplývá, že tento problém je více staticky neurčitý než rovnočelný plát.
Základní doporučení při návrhu plátu
Z provedených výpočtů a experimentů vyšly následující poučky:
- Čím je sklon čela menší, tím je statické chování plátu lepší (bohužel se tím plát prodlouží).
- U šikmočelného plátu postačují buď 4 kolíky, nebo 3 spojovací prostředky složené kombinací hmoždíků a kolíků. Větší počet nezvětšuje únosnost plátu.
- Plát s hmoždíky musí mít zabráněno rozevírání způsobené rotací hmoždíku. To je řešeno podkoseným čelem, kolíkem, nebo jejich kombinací.
- Plát namáhaný normálovou silou je vhodné zabezpečit hmoždíkem
- Únosnost plátu, kde je použit hmoždík, je mírně vyšší oproti plátu s kolíky.
- Délka plátu významně ovlivňuje jeho únosnost, naopak tuhost není ovlivněna téměř vůbec.
- Delší plát má větší únosnost než kratší.
- Vzdálenosti spojovacích prostředků musí být min. 7Ø od čela.
Pokud přihlédneme k výrobním postupům, pak sklon čela 45° je nejvhodnější co se týče výroby a délky, staticky je také dostatečný. Délka plátu se může pohybovat v rozmezí 3h–6h, kde únosnost delšího plátu 6h při převažujícím momentu je téměř dvojnásobná oproti menšímu 3h. Při převažující posouvající síle je výhoda delšího plátu menší.
4. Porovnání experimentálních a teoreticky vypočtených výsledků
Tvar testovaného trámu je na obr. 5. Nosník byl zkoušen v tříbodovém ohybovém testu v laboratořích Teoretické a Aplikované Mechaniky v Praze (UTAM). Více se lze dočíst v [4, 8, 9].
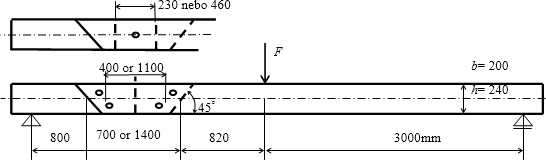
Obr. 5 Testovaná konstrukce – nahoře dva hmoždíky a jeden kolík dole 4 kolíky
Únosnost – první mezní stav
Únosnost spoje závisí na modech porušení, které byly získány z několika desítek provedených experimentů. Nejčastějším bylo rozštěpení čela obr. 6 vlevo, dalším bylo porušení kolíku obr. 6 vpravo, nebo v okolí kolíku a v neposlední řadě se jednalo o porušení tahem v oslabeném průřezu obr 7.
- Mezní síla v čele je odvozena ve tvaru V = A . fck90 = 0,5 . l . b/2 . fck90, kde l je vzdálenost spojovacího prostředku od čela, a dále je uvažován i vliv výsušných trhlin hodnotou 0,5, která je v souladu s experimenty na trámech uložených v běžných vlhkostních poměrech s rozměry používanými ve stavební praxi.
- Maximální zatížení kolíku závisí na jeho průměru a materiálu – pro průměr 24 mm je Fx = 5,8 kN, Fz = 3,25 kN pro hmoždík 50×50 mm je Fx = 30 kN, M = 4,6 kNm.
- Tahové napětí v ohybu je omezeno v souladu s experimentem na σ = 40 MPa.
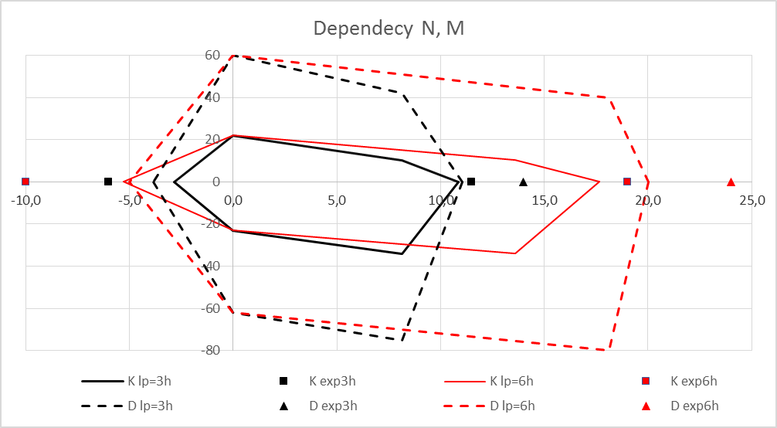
V grafu na obr. 8 je vykreslena vypočítaná závislost momentu a normálové síly pro dva spoje různých délek. Plnou čarou jsou vykresleny výsledky 4kolíkového spoje s délkou plátu 3h a 6h. Čárkovanou čárou jsou výsledky spoje s dvěma hmoždíky a jedním kolíkem. V souladu s uvedenými zjednodušujícími podmínkami se jedná o lineární stav. K vyčerpání únosnosti dochází při větším zatížení tzv. mezní únosnosti, kdy nosník přechází postupně do plastického stavu. V prováděných experimentech byla plastická rezerva přibližně 20 %.
Graf potvrzuje doporučení ohledně délky plátu, kde únosnost delšího plátu je výrazně větší. Potvrzuje také rozdíl mezi únosnosti plátu pouze s kolíky, nebo plátu s hmoždíky a kolíkem. Experimentální výsledky jsou označeny značkou. Více naměřených údajů je doposud k dispozici jen u čtyřkolíkového spoje.
Důležitým poznatkem je to, že výpočtem vychází mírně menší únosnost než v experimentu, což je na straně bezpečné.
Průhyb – druhý mezní stav
| Flin [kN] | u lin [mm] | k = F/u | Redukce k [%] | ulin [mm] | k = F/u | Redukce k [%] | |
|---|---|---|---|---|---|---|---|
| Experiment | Délka plátu Lp = 6h | Délka plátu Lp = 3h | |||||
| 4× kolík | 22.7 | 50.3 | 450 | 11.5 | 49.4 | 462 | 7 |
| 2× hmoždík + kolík | 22.7 | 50.5 | 444 | 12.5 | 49.3 | 460 | 7 |
| Bez spoje | 22.7 | 45.1 | 508 | – | |||
| Flin [kN] | u lin [mm] | k = F/u [MN/m] | Redukce k [%] | ulin [mm] | k = F/u | Redukce k [%] | |
|---|---|---|---|---|---|---|---|
| Výpočet pro C22 | Délka plátu Lp = 6h | Délka plátu Lp = 3h | |||||
| 4× kolík | 22.7 | 54.2 | 420 | 18 | 52.3 | 433 | 15 |
| 2× hmoždík + kolík | 22.7 | 52.2 | 435 | 15 | 50.0 | 464 | |
| Bez spoje | 22.7 | 45.4 | 500 | – | |||
V tabulce 1 jsou vypsány naměřené výsledky z experimentů, v tabulce 2 jsou výsledky vypočítané podle teoretického modelu – viz [4–6].
Shoda výpočtu s experimentem je dostatečná pro použití v praxi. Výpočet uvádí mírně větší průhyby, což je na straně bezpečné. V tabulkách jsou porovnány nosníky nastavené plátem s referenčním nosníkem bez plátu. To umožňuje v praxi jednoduchý návrh nosníku s plátem. Stačí vypočítat průhyb na nosníku bez plátu a poté vypočtené průhyby přenásobit korekčním součinitelem. Pro daný nosník by byl 1,1 až 1,18.
5. Diskuze nad výsledky
- Výsledky výpočtů a experimentů jsou v dobré shodě.
- Nejčastěji se plát porušuje štěpením konce s výsušnou trhlinou. Zde je možné zvýšit únosnost pomocí příčného zavrtání vrutů viz [10].
- Pokud je rozhodující 1. mezní stav únosnosti, je lepší použít spoj s hmoždíky.
- Při namáhání trámu normálovou silou je spoj s hmoždíky vhodnější než jen s kolíky.
- Pokud je rozhodující 2. mezní stav použitelnosti, je možné použít libovolný spoj i spoj s kratší délkou.
Poděkování
Článek je napsán za podpory grantu Ministerstva Kultury NAKI projekt – DF12P01OVVOO4 – Návrh a posuzování dřevěných tesařských spojů historických konstrukcí.
Literatura
- [1] Petr Kuklík, Hana Hasníková, Metody pro zjišťování spolehlivosti historických dřevěných konstrukcí, 1801-4399, TZB-info – 3/2013, http://stavba.tzb-info.cz/drevene-a-ocelove-konstrukce/9669-metody-pro-zjistovani-spolehlivosti-historickych-drevenych-konstrukci.
- [2] Michal Kloiber, Jiří Bláha, Jiří Kunecký, Hana Hasníková, Jan Tippner, Václav Sebera: Navrhování celodřevěných spojů na příkladu opravy krovu kostela Nanebevzetí Panny Marie ve Vranově nad Dyjí. ISSN 1210-5538, Zprávy památkové péče – 73/2, str. 132–139, počet s. 8, 2013.
- [3] Gerner, M.: Tesařské spoje, 1. vydání. Praha, Grada, 2003. ISBN 80-247-0076-X.
- [4] Karel Šobra, Petr Fajman, Jiří Máca: Experimentální a numerická analýza styku kulatiny pomocí přeplátování, 1210-4027, Stavební obzor – 3/2013, s. 61–65, ČVUT.
- [5] Petr Fajman: Rozložení sil v plátovém spoji od ohybového momentu, 1210-4027, Stavební obzor – 4/2013, s. 101–104, ČVUT.
- [6] Petr Fajman: Vliv tuhosti svorníku na síly v plátovém spoji, ISSN 1210-4027, Stavební obzor – 7,8/2014, s. 115–120, počet s. 6. ČVUT.
- [7] Fajman, P., Maca, J.: The effect of key stiffness on forces in a scarf joint, ISSN 1759-3433, Proceedings of the Ninth International Conference on Engineering Computational Technology, 2014, 16 p., Stirling, Civil-Comp Press Ltd.
- [8] Milch, J., Tippner, J., Brabec, M., Sebera, V.: Experimental Verification of Numerical Model of Single and Double-Shear Dowel-Type Joints of Wood, ISBN 978-0-9817876-4-0, 57th International Convention of Society of Wood Science and Technology 2014, pp. 368–376, Monona, Society of Wood Science and Technology.
- [9] Kunecky, J., Sebera, V., Tippner, J., Arciszewska-Kędzior, A., Hasnikova, H., Kloiber, M.: Experimental assessment of historical full-scale timber joint accompanied by a finite element analysis and digital image correlation, ISSN 0950-0618, Construction and Building Materials 2015.
- [10] Lokaj, A., Klajmonová, K.: Poznatky z testování vybraných spojů kulatiny, 1801-4399, TZB-info – 2015
http://stavba.tzb-info.cz/drevostavby/12975-poznatky-z-testovani-vybranych-spoju-kulatiny
Článek se zabývá aktuální problematikou sanace poškozeného dřevěného nosníku pomocí nastavovacího plátového spoje s hmoždíky a kolíky. Autor článku uvádí teoretický rozbor několika variant řešení nastavovacího plátového spoje sanovaného nosníku. Teoretický výpočet je srovnán s řadou provedených experimentů. Výsledky experimentů prokázaly dobrou shodu s teoretickými výpočty. Autor článku uvádí řadu užitečných doporučení pro praktický návrh nastavovacího plátu, které vycházejí z teoretického rozboru i provedených experimentů. Článek je po obsahové i formální stránce zpracován velmi kvalitně.
During the renovation of ceiling joists and roof structures in historic buildings, decayed wood must often by replaced by new one. To preserve as much original material as possible, the lapped scarf joint may be used. The knowledge of its behaviour is essential for its design process – the shape, type of joint and the number of connecting tools. Unfortunately, this joint has not been adequately examined in structural terms yet. A simplified analytical model is derived in the article. The data obtained from experiments are a necessary addition for the simplification of the designed model. The resulting solution complies with the real behaviour of the scarf joint.