Předpjatá trubková ocelová vzpínadla s jedním křížem
Tento článek je zaměřen na experimenty se vzpínadly, numerické analýzy a jejich vyhodnocení. V teoretické části je uvedena lineární bifurkace (2D LBA) ke stanovení kritických sil a tvarů vybočení, geometricky nelineární analýza ke stanovení únosnosti imperfektních vzpínadel (3D GNIA) a geometricky a materiálově nelineární analýza ke stanovení únosnosti imperfektních vzpínadel z nerezových ocelí (3D GMNIA). Numerické výpočty jsou provedeny v softwaru ANSYS a validovány na experimentech. Parametricky jsou vyšetřeny vlivy počátečních průhybů, směru vybočení, materiálové nelinearity a způsobu uložení táhel na středovém kříži. Výsledky jsou shrnuty v praktická doporučení. Článek navazuje na předchozí obecné pojednání o předpjatých ocelových tlačených trubkách s jedním křížem (Macháček [1]).
1. Úvod
Předpjaté vzpínadlové pruty umožňují dosažení extrémních štíhlostí při potřebné únosnosti. Pro návrh takového prutu je však nutné vzít v úvahu zvýšené náklady na výrobu a montáž a také vnímat návrh z hlediska estetiky. Současné materiály a možnosti předpínání mohou vést k exkluzivní konstrukci, poměrně nenákladné i estetické. Často jsou realizovány vzpínadlové prvky z nerezových trubek (z austenitické, duplexní, nověji i nízkolegované nebo feritické oceli), zatímco vlastní předpínací prvky nabízí řada výrobců a distributorů (systémy Macalloy, DETAN, Pfeifer a další). Pro táhla vzpínadel je možné použít tyče nebo lana (lana mohou být na příčných křížích kotvena, nebo probíhat spojitě přes sedla – toto řešení je úsporné, obvykle však snižuje únosnost). Napínací systémy a kontrolu předpětí nabízejí distributoři předpínacích prvků, popř. odborná pracoviště.
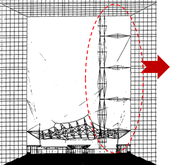
Při návrhu je nutné rozlišovat ztrátu stability „ideálního“ (dokonale přímého) prutu při dosažení kritického zatížení, únosnost „skutečného“ (imperfektního) prutu dosažené při jeho kolapsu, popř. návrhové únosnosti podle návrhových norem. Tyto pojmy a obecné možnosti uspořádání vzpínadlových prutů a křížů uvádí podrobněji předchozí článek (Macháček [1]), který se zabýval chováním a návrhem vzpínadlového prutu s jedním centrálním křížem, analytickým řešením kritických sil a doporučeními k návrhu imperfektních vzpínadel (podle Wadeeho a kol. [2]), včetně řešení příkladu. Na obr. 1 vlevo je uveden příklad vzpínadla s jedním křížem. Větší počet příčných křížů (viz obr. 1 vpravo) umožňuje další zvýšení štíhlosti a vyšší únosnost než vzpínadlo s jedním centrálním křížem (článek autorů týkající se vzpínadel se dvěma kříži je v tisku).

Obr. 1 Vzpínadla s jedním křížem stabilizující výtah Grande Arche v Paříži (vlevo a uprostřed), vzpínadla se třemi kříži na stadionu Estádio Algarve ve Faru (vpravo)
Tento návazný článek popisuje numerické přístupy k řešení stability a únosnosti vzpínadlových prutů s jedním křížem, experimentální vyšetřování vzpínadlového prutu v laboratoři a validaci numerické analýzy po srovnání s výsledky testů. V parametrických studiích uvádí vyhodnocení efektivity vzpínadlových prutů z různých hledisek (podle směru vybočení centrální trubky, vlivu počátečních imperfekcí, velikosti předpětí a použitého materiálu trubek i táhel, způsobů uložení táhel na středovém kříži).
2. Experimentální vyšetřování
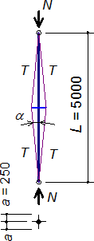
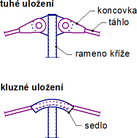
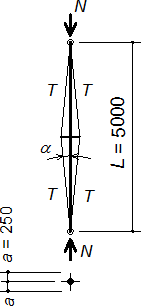
V laboratoři Fakulty stavební ČVUT byly testovány 4 trubkové vzpínadlové pruty s jedním křížem a shodného geometrického tvaru, avšak s různým předpětím, obr. 2. (Servítová a Macháček [3]). Vzpínadlový prut tvořila centrální trubka namáhaná tlakem N, navařený kříž z trubek se čtyřmi rameny v úhlu 90º a čtyři lanková táhla probíhající kluzně (spojitě) přes sedla na kříži. Do každého lanka bylo vneseno předpětí T.
Hlavní rozměrové a materiálové charakteristiky:
- Centrální trubka: Ø 50×2 [mm], nerezová ocel 1.4301 (L = 5000 mm, Ac = 302 mm2, Ic = 87009 mm4, Ec,ini = 184 GPa).
- Kříž: Ø 25×1,5 [mm], nerezová ocel 1.4301 (a = 250 mm, Aa = 111 mm2, Ia = 7676 mm4, Ea,ini = 184 GPa).
- Táhla: Macalloy lanka Ø 4 mm, 1×19 nerezová ocel SC460 (Ls = 2513 mm, As = 12,6 mm2, Es,ini = 107 GPa).
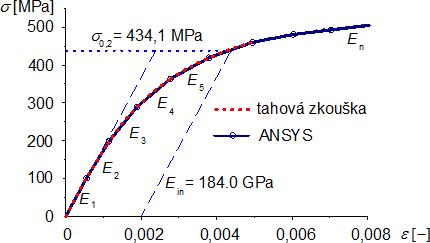
Uvedené počáteční moduly pružnosti trubek byly zjištěny z tahových vzorků s průřezem celých trubek, zatímco počáteční modul pružnosti lanek byl převzat z materiálu společnosti Macalloy. Pracovní diagram získaný ze zkoušek 3 vzorků a polygonální aproximace pro numerické řešení v softwaru ANSYS jsou zobrazeny na obr. 3.
Předpětí bylo do táhel vneseno napínáky s kalibrovanými tenzometry a jeho velikost byla volena náhodně, pro pocit dostatečného, praktického vypnutí. Před každou zkouškou byly u každého prutu po předpětí změřeny počáteční tvary a amplitudy počátečních prohnutí pomocí elektrických potenciometrů a kontrolně 3D skenováním. Zatěžování prutů probíhalo ve stupních po 2,5 kN s následným odlehčením a bylo ukončeno po dosažení nadměrné hodnoty příčného průhybu. Grafické znázornění průběhu testů vzpínadlových prutů je uvedeno u validace numerického řešení (odst. 4.1) a experimentální výsledky jsou shrnuty následovně (Píchal a Macháček, [3]):
- Vzpínadlo 1.: Průměrné předpětí jednoho táhla T = 1,360 kN (celkem 5,44 kN).
Amplituda největšího počátečního prohnutí w0y = 1,9 mm, w0z = 8,3 mm
Maximální únosnost Nmax = 17,7 kN. - Vzpínadlo 2.: Průměrné předpětí jednoho táhla T = 1,135 kN (celkem 4,54 kN).
Amplituda největšího počátečního prohnutí w0y = 3,8 mm, w0z = 19,9 mm.
Maximální únosnost Nmax = 14,9 kN. - Vzpínadlo 3.: Průměrné předpětí jednoho táhla T = 0 kN (bez předpětí).
Amplituda největšího počátečního prohnutí w0y = 0,3 mm, w0z = 1,4 mm.
Maximální únosnost Nmax = 6,5 kN (pozn. Eulerovo břemeno NE = 6,3 kN). - Vzpínadlo 4.: Průměrné předpětí jednoho táhla T = 0,975 kN (celkem 3,90 kN).
Amplituda největšího počátečního prohnutí w0y = 0,5 mm, w0z = 2,2 mm.
Maximální únosnost Nmax = 16,2 kN.
Tvar počátečních průhybů se u všech prutů blížil tvaru jedné sinusové polovlny a v průběhu zatěžování zůstal tento tvar zachován (nikdy nedošlo k „přeskoku“ do jiného tvaru vybočení).
3. Teoretické vyšetřování
3.1 Lineární bifurkace nepředpjatého vzpínadlového prutu
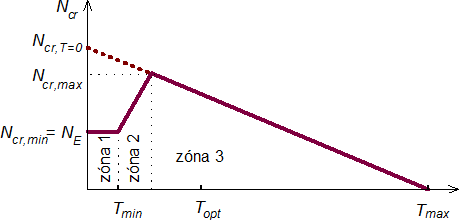
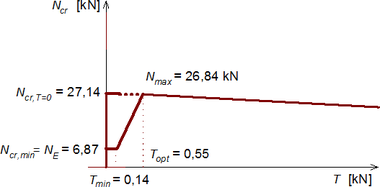
Obr. 4 Kritické zatížení „ideálního“ vzpínadla v závislosti na předpětí táhel
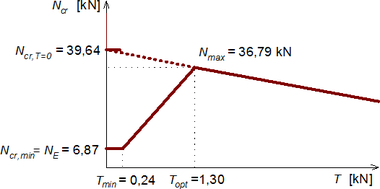
K řešení lineární pružné stability „ideálního“ nepředpjatého vzpínadlového prutu Ncr,T=0 lze použít jednoduchou lineární bifurkační analýzu (LBA). Pro předpjaté vzpínadlové pruty je však nutné použít geometricky nelineární analýzu (GNA), neboť kromě závislosti na velikosti předpětí dochází při určitých předpětích při vybočení k náhlým změnám vnitřní energie prutové soustavy, kterou nelze prostředky LBA zahrnout. Jak ukazuje graf na obr. 4, předpětí (v každém táhle označeno písmenem T) vymezuje 3 oblasti chování vzpínadlového prutu.
V zóně 1 je předpětí velmi nízké (T < Tmin), takže při zatížení tah v táhlech vymizí, prut se chová jako bez táhel a kritické zatížení prutu dosáhne pouze Eulerovy síly NE = Ncr,min.
V zóně 2 je předpětí větší než minimální Tmin, ale menší nebo rovné optimálnímu předpětí Topt, při kterém má kritické napětí největší hodnotu Ncr,max. Předpětí v táhlech na konkávní straně vybočení je v této oblasti aktivní (nenulové) pouze do okamžiku vybočení.
V zóně 3 je předpětí větší než optimální Topt. V tomto případě zůstávají všechna táhla po vybočení aktivní (napjatá). Účinek předpětí v táhlech zvyšuje zatížení a tím snižuje kritické napětí prutu.
Podrobnosti k analytickému řešení velikosti kritické síly podle Hafeze a kol. [4], včetně stanovení optimálního předpětí a tvaru vybočení, jsou uvedeny v článku prvního autora (Macháček [1]).
Bifurkační analýza nepředpjatého experimentálního vzpínadla (2D LBA) byla provedena v softwaru Scia Engineer. Parametry centrální trubky, kříže i táhel odpovídají experimentálním vzpínadlům, táhla jsou uvažována aktivní pro tah i tlak. Ukázány jsou první tři tvary vybočení a odpovídající kritické síly pro vzpínadla jak s tuhým, tak i kluzným uložením táhel na kříži.
V prvním případě (obr. 5) byl zaveden modul pružnosti všech částí zjednodušeně, jednotně hodnotou E = 200 GPa (odpovídá nerezové oceli podle ČSN EN 1993-1-4). Odpovídá tedy táhlům z tyčí, u nichž kluzné uložení nelze realizovat.
V druhém případě (obr. 6) byl pro táhla zaveden modul pružnosti E = 107 GPa (odpovídá sekantové hodnotě modulu pružnosti lanek Macalloy podle specifikace Tension Systems – „Systém konstrukčních táhel Macalloy“), pro centrální trubku a kříž byly ponechány hodnoty E = 200 GPa.
Z výsledků je zřejmý značný vliv modulu pružnosti táhel nejen na velikost kritických sil, ale i na odpovídající způsob vybočení. Tyto závislosti byly podrobně zkoumány v počátcích lineárního vyšetřování vzpínadlových prutů, např. Hafezem a kol. [4].
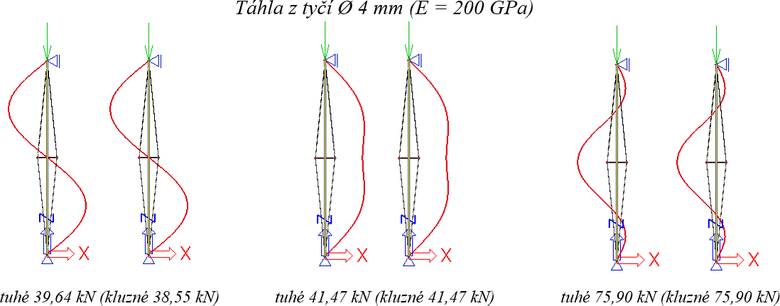
Obr. 5 První tři kritické síly Ncr,T=0 a tvary vybočení podle LBA pro táhla z tyčí a tuhé i kluzné uložení táhel na křížích
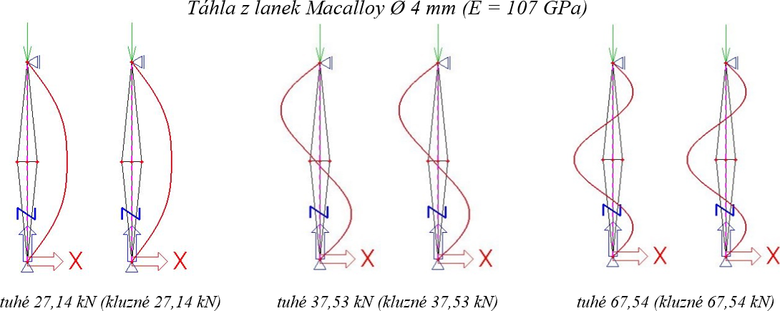
Obr. 6 První tři kritické síly Ncr,T=0 a tvary vybočení podle LBA pro táhla z lan a tuhé i kluzné uložení táhel na křížích
3.2 Analytická aproximace kritického zatížení předpjatého vzpínadlového prutu
Kritické zatížení a odpovídající optimální předpětí „ideálního“ vzpínadlového prutu s jedním křížem uprostřed délky odvodili Smith a kol. [5], které doplnili Hafez a kol. [4] a je podrobně, včetně numerického příkladu, uvedeno v [1]. Pro odvození platí: Prut je ideálně přímý, kloubově uložený, bez imperfekcí, přípoje křížů k prutu jsou tuhé, všechny přípoje táhel jsou kloubové a osová deformace křížů je zanedbána. Není účelné znovu opakovat celé odvození a výsledné vzorce. Nicméně pro parametry experimentálního vzpínadla a srovnání s předcházejícími výsledky 2D LBA a následujícím řešením 3D GNIA, resp. 3D GMNIA, jsou zopakovány výsledky z níže uvedených publikací (obr. 7):
- Pro jednotný modul pružnosti centrální trubky, kříže i táhel E = 200 GPa vychází podle Píchala a Macháčka [6] optimální předpětí Topt = 1,30 kN a kritická síla Ncr,max = 36,79 kN. Rozhodující tvar vybočení je přitom antisymetrický.
- Pro modul pružnosti centrální trubky s křížem E = 200 GPa a modul pružnosti táhel E = 107 GPa vychází podle Macháčka [1] optimální předpětí Topt = 0,55 kN a kritická síla Ncr,max = 26,84 kN. Rozhodující tvar vybočení je přitom symetrický.
Táhla E = 200 GPa
Ncr,max = 36,79 kN
Topt = 1,30 kN
Lanová táhla E = 107 GPa
Ncr,max = 26,84 kN
Topt = 0,55 kN
Obr. 7 Výsledky analytického řešení a rozhodující tvar vybočení
Získané výsledky jsou přehledně uvedeny na obr. 8. Je však nutné znovu připomenout, že tato řešení platí pro „ideální“ vzpínadlový prut, tedy bez počátečních průhybů.
Obr. 8 Výsledky 2D LBA (pro nulové předpětí) a analytického řešení (pro celý rozsah předpětí)
3.3 Nelineární numerická analýza ve 3D
Nelineární analýza byla provedena v softwaru ANSYS. Pro centrální trubku a kříže byly použity prutové elementy BEAM188 a pro táhla prvek LINK188 (s volbou aktivní jen pro tah), kloubově připojenými ke konci centrální trubky. V průběhu řešení byly zkoumány oba případy spojení táhel s rameny kříže: tuhá táhla kloubově připojená ke křížům a lanová táhla probíhající průběžně přes sedla na křížích (jak bylo realizováno při testech). Z hlediska praktické volby je druhé řešení levnější a jednodušší, ukázalo se však, že méně únosné při antisymetrickém vybočení centrální trubky. V tomto případě jsou sedla na ramenech kříže vytvořena z plošných elementů SHELL281 (obr. 9), vytvářející příslušný tvar sedel. Ta jsou pokryta prvky TARGE170, zatímco lana v příslušném zakřivení prvky CONTA175 (Macháček a Píchal, [4]). Kontaktní úloha byla řešena penalizační metodou (Pure Penalty), umožňující regulovat prokluz mezi lanem a sedlem pomocí součinitele tření (uvažovány byly hodnoty mezi 0,01 až 0,10, pokrývající teflonové až ocelové povrchy).
Všechny uvedené konečné prvky disponují velkými deformacemi a plasticitou, umožňující řešení GMNIA (geometricky a materiálově nelineární analýzou s imperfekcemi). V numerickém řešení GMNIA byl proto pro centrální trubku a kříž zaveden materiál podle obr. 3, pro táhla jejich modul pružnosti Es,ini. Optimalizace sítí konečných prvků vedla k osovému dělení pro trubky L/250 a a/25 (geometrie viz obr. 2), zatímco u plošných prvků sedel na plochy o velikosti zhruba 23 mm2.
Po zavedení požadovaných počátečních průhybů bylo předpětí docíleno ochlazením táhel. Pro testovaná vzpínadla bylo aplikováno ochlazení na dané předpětí, pro parametrické studie obvykle pro 30 teplotních hodnot, pokrývajících požadované spektrum předpětí. Ochlazení z pokojové na danou teplotu bylo vždy provedeno v 10 krocích k obnovení rovnováhy na deformovaném vzpínadle a poté bylo aplikováno vnější zatížení na centrální prut. Pro každý stupeň zatížení se použila Newton-Raphsonova iterace (N-R) s limitem 1000 iterací, popř. do splnění konvergenčního limitu.
4. Validace numerické analýzy na výsledcích testů
Testované trubky měly na křížích sedla a táhla byla průběžná. V prvním kroku numerické analýzy byla zavedena počáteční prohnutí centrální trubky ve tvaru jedné sinusové polovlny s amplitudami uvedenými v kap. 2. Celkové uvedené experimentální předpětí bylo poté v několika aproximacích rozděleno do jednotlivých táhel (jejich ochlazením) tak, aby výsledné amplitudy počátečních prohnutí a celkové předpětí odpovídaly změřeným hodnotám.
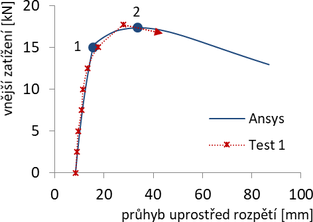
Vzpínadlo č. 1: Celkové předpětí všech táhel bylo 4T = 5,44 kN. Na obr. 10 je zobrazen vztah mezi vnějším zatížením a průhybem uprostřed centrální trubky (jedná se o maximální průhyb v prostoru, mezi rameny kříže). Průběh k bodu 1 byl téměř lineární, poté došlo k vybočení a rychlému nárůstu průhybu až do dosažení maximální únosnosti Nmax,exp = 17,7 kN (bod 2). Poté již následoval enormní průhyb a odtížení. Numerická analýza GMNIA velmi dobře koresponduje s celým průběhem testu a dává Nmax = 17,3 kN.
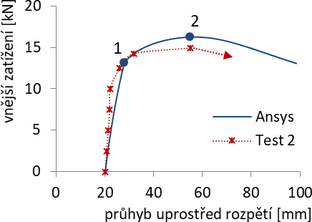
Vzpínadlo č. 2: Celkové předpětí všech táhel bylo 4T = 4,54 kN. Vztah mezi zatížením a centrálním průhybem byl víceméně lineární až do zatížení 12,5 kN, poté došlo k rychlému nárůstu deformací a dosažení maximální únosnosti Nmax,exp = 14,9 kN (bod 2). Numerické řešení GMNIA dává hodnotu Nmax = 16,2 kN (překročení experimentální únosnosti o 9 %).
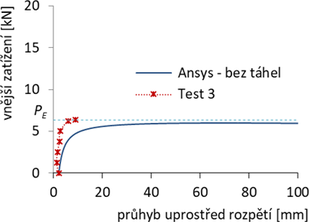
Vzpínadlo č. 3: Tento test proběhl bez jakéhokoliv předpětí, tj. táhla byla zcela uvolněna. Účelem bylo potvrdit Eulerovské chování prostě podepřeného prutu. Počáteční prohnutí bylo velmi malé (viz kap. 2) a Eulerova síla je NE = 6,3 kN. Test byl ukončen po náhlém vybočení prutu, které odpovídalo zatížení Nmax,exp = 6,5 kN (tj. odchylka od Eulerovy síly o 2.8 %). Numerická analýza GMNIA pro daný, počátečně zakřivený prut, dává maximální zatížení Nmax = 6,0 kN < NE, viz obr. 11.
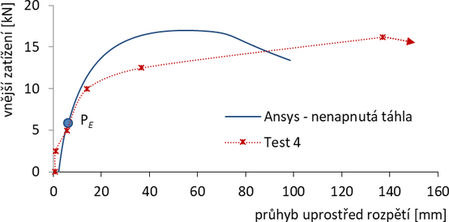
Vzpínadlo č. 4: Tato zkouška proběhla po ukončení testu č. 3, se stejným prutem, avšak pro táhla velmi mírně předepnutá tak, aby vzpínadlo bylo napřímeno do minimálního počátečního průhybu (viz kap. 2). Celkové předepnutí všech čtyř táhel tak činilo 3,9 kN. Počáteční fáze, zhruba do zatížení 10 kN, vykazovala téměř lineární chování, poté však došlo k enormnímu růstu deformací až do dosažení maximálního zatížení Nmax,exp = 16,2 kN. Pro numerické řešení byl volen tentokrát jiný přístup, táhla byla modelována, avšak zcela bez předpětí (jako uvolněná). Po vybočení vzpínadla se táhla na konvexní straně aktivovala a výsledná maximální síla činí Nmax = 17,0 kN. Ve srovnání s případem č. 3 tak byl potvrzen kladní efekt táhel i bez předpětí (maximální únosnost se zvýšila z 6,0 kN na 17,0 kN).
Provedená validace numerické analýzy GMNIA tak byla na základě těchto čtyř testů úspěšná.
5. Numerické studie GNIA a GMNIA
Předchozí článek (Macháček [1]) uvádí pro vzpínadlové pruty s jedním křížem uprostřed rozpětí podrobnosti k analytickému řešení stability (tj. řeší kritické zatížení „ideálních“ prutů) a přibližné vztahy pro únosnosti „imperfektních“ prutů při libovolném předpětí (podle Wadeeho a kol. [5]). Zatímco tato řešení byla provedena v jedné rovině ramen kříže (tj. ve 2D), následující řešení ukazuje výsledky numerického řešení podle kap. 3 ve 3D. Zabývá se tedy i vlivem prostorového vybočení mezi rameny kříže a také vlivem uložení táhel na kříži (tuhé nebo kluzné). Je nutné znovu připomenout, že pro řešení kritických zatížení ideálních vzpínadel i skutečné únosnosti imperfektních vzpínadel v celém rozsahu předpětí je nutné použít nelineární geometrickou analýzu, neboť při aplikaci předpětí (zejména v zóně 2 (podle obr. 4), popř. při přeskocích tvarů vybočení) dochází k náhlé změně vnitřní energie prutu.
Kritické zatížení vzpínadla (tj. pro „ideální“ přímý prut), proto vyžaduje geometricky nelineární řešení s „infinitesimální“ (téměř nulovou) velikostí počátečního průhybu, jehož hodnota byla zvolena v obou směrech ramen kříže w0y = w0z = L/500000 = 0,01 mm.
Reálná únosnost vzpínadla (tj. pro „imperfektní“, počátečně zakřivený prut), byla řešena pro počáteční průhyb požadovaný Eurokódem ČSN EN 1993-1-1 pro za studena tvarované trubky řešené pružnou analýzou s tím, že hodnota tohoto průhybu mezi rameny kříže (v prostoru) je w0 = L/200 = 25,0 mm.
Řešení 3D GNIA (pro nerezové trubky 3D GMNIA) v celém rozsahu možných předpětí vyžaduje pro každé předpětí (řádově 30–40 hodnot) volit vhodné stupně vnějšího zatížení (řádově 1000 stupňů) a pro každý stupeň značné množství N-R iterací (limit 1000 iterací, viz kap. 3.3). Výpočty proto vyžadovaly výkonný počítač a značný výpočetní čas. Detailní řešení bylo proto provedeno pouze pro geometrické charakteristiky vzpínadel uvedené v kap. 2 (centrální trubka Ø 50×2 [mm], ramena kříže Ø 25×1,5 [mm], táhla Ø 4 mm).
5.1 Vliv směru vybočení
Testy provedené autory (kap. 2 a 4) vedly vždy k vybočení mezi ramena kříže (do prostoru). Všechny dosud publikované zahraniční výsledky jsou řešeny ve 2D (v rovině ramen křížů). Bylo proto žádoucí prokázat numericky nižší únosnost pro vybočení do prostoru, kde se může předpokládat nižší tuhost. Autoři publikovali srovnání únosnosti pro vybočení v rovině ramen kříže a do prostoru v [7], odkud však vyplynulo, že únosnosti jsou téměř stejné, rozdíl je zcela zanedbatelný. Nicméně pro následující studie byl zaveden vždy prostorový počáteční průhyb, s amplitudou w0 (tj. w0y = w0z = w0 / √2), neboť uvedená sofistikovaná analýza ve 3D to umožňovala.
5.2 Vliv tvaru nebo velikosti amplitudy počátečního průhybu a vliv materiálové nelinearity
Pro výše uvedené parametry vzpínadla byly provedeny studie 3D GNIA a 3D GMNIA, které dokladují význam počátečního průhybu. Pro zjednodušení byla analyzována pouze fiktivní tyčová táhla, přičemž pro 3D GNIA byl zaveden jednotný modul pružnosti E = 200 GPa podle doporučení ČSN EN 1993-1-4, zatímco pro 3D GMNIA byl použit pracovní diagram nerezové oceli podle obr. 3. Výsledky únosností (maximálních dosažených zatížení dosažených pro příslušnou „optimální“ hodnotu předpětí) jsou uvedeny v Tab. 1 (v úvodu tabulky jsou pro srovnání uvedeny analytické hodnoty podle Hafeze a kol. [4] a uvedené v kap. 3.2).
w0 [mm] | Symetrický tvar | Antisymetrický tvar | Analýza | ||
|---|---|---|---|---|---|
| Topt,sym [kN] | Nmax,sym [kN] | Topt,anti [kN] | Nmax,anti [kN] | ||
| 0 | 1,41 | 39,79 | 1,30 | 36,79 | Hafez [4] |
| 0,01 | 1,51 | 39,73 | 1,35 | 36,18 | GNIA |
| 0,05 | 1,58 | 39,25 | 1,43 | 35,77 | GNIA |
| 0,10 | 1,61 | 38,62 | 1,52 | 35,43 | GNIA |
| 25,0 | – | 22,74 | – | 24,84 | GNIA |
| 0,01 | 1,51 | 36,54 | 1,27 | 31,58 | GMNIA |
| 25,0 | – | 19,57 | – | 19,92 | GMNIA |
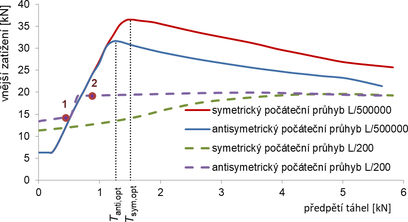
V souladu s kritickým tvarem podle obr. 5 rozhoduje pro velmi malé amplitudy počátečních průhybů antisymetrický tvar vybočení. Výsledky pro takové amplitudy symetrického i antisymetrického tvaru se téměř shodují s analytickým řešením podle Hafeze a kol. [4]. Pro velké amplitudy počátečních průhybů (w0 = L/200) však převáží vybočení v celé délce vzpínadla a rozhodující nižší únosnost dává potom symetrický počáteční průhyb (je dobré si připomenout stejný vliv měkkých lanových táhel, viz obr. 8).
Tabulka únosností ukazuje jedinou hodnotu pro příslušné předpětí. Obr. 12 proto ukazuje hodnoty dosažených zatížení v celém spektru předpětí podle 3D GMNIA. Zřejmý je enormní význam zejména amplitudy počátečního průhybu, kde křivky pro reálné amplitudy (L/200) jsou převážně (pro vyšší předpětí) velmi nízko. Poučné jsou však vyšší hodnoty únosností pro reálné amplitudy ve srovnání s únosnostmi pro infinitesimální amplitudy (L/500000, tj. „kritické“ hodnoty) pro malá předpětí (platí i pro zcela nepředpjaté vzpínadlo). Je to způsobeno aktivací táhel na konvexní straně při vybočení vzpínadla (podobné závěry zmínili Wadee a kol. [2]). Znamená to, že i vzpínadlo se zcela nepředepnutými táhly má vyšší únosnost než je jeho kritické zatížení.
Pro antisymetrický tvar velkého počátečního průhybu lze při nízkých předpětích pozorovat tendenci k „přeskoku“ z antisymetrického do symetrického tvaru vybočení (oblast mezi body 1 a 2). U větších předpětí je však vybočení již zásadně ve tvaru počátečního průhybu (antisymetrické).
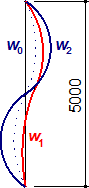
Obr. 12 Vztah mezi dosaženým zatížením a předpětím podle 3D GMNIA (nerezový materiál). Vpravo je tvar průhybů vzpínadla pro předpětí odpovídající bodům 1 a 2
5.3 Vliv způsobu uložení táhel na středovém kříži
Použití lanových táhel umožňuje jejich kluzné vedení v sedle na středovém kříži. Takové uspořádání je výhodné z hlediska konstrukce i montáže vzpínadla. Počet dílců (táhel a koncovek) je poloviční a napnutí lan přes sedlo je úspornější než kotvení. Většina provedených vzpínadel však používá tyčová táhla, neboť je zřejmé, že nízký modul pružnosti lan a jejich prokluz v některých případech vybočení únosnost vzpínadla snižuje.
Pro porovnání kritické síly vzpínadel s tuhým nebo kluzným uložením táhel na sedlech kříže byla proto provedena pilotní studie 2D LBA. První tři kritické síly a odpovídající tvary vybočení jsou ukázány na obr. 5 a obr. 6. Porovnání výsledků s lanovými táhly (E = 107 GPa, Ø 4 mm) a tyčovými táhly (E = 200 GPa, Ø 4 mm) ukazuje na významný vliv modulu pružnosti. Pro lanová táhla je první kritický tvar symetrický (oproti antisymetrickému u tyčových táhel) a pokles kritické síly činí 32 %. Vliv kluzného oproti tuhému uložení se u kritických sil neprojevuje, s výjimkou prvního antisymetrického tvaru vybočení – je však nevýznamné (lze vysvětlit prokluzem kluzného uložení při deformaci ramen kříže). Větší rozdíl u antisymetrického tvaru vybočení však ukazuje následující případ nerezového vzpínadla.
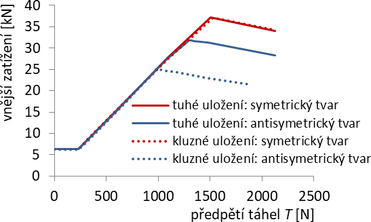
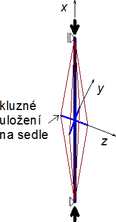
Obr. 13 Vliv kluzného uložení táhel v sedlech na středovém kříži podle 3D GMNIA. Počáteční průhyb hlavní trubky s amplitudou w0 = L/500000 = 0,01 mm. Součinitel tření v sedlech ν = 0,01.
Nelineární analýza 3D GMNIA pro „ideální“ vzpínadlo s počátečním infinitesimálním průhybem w0 = L/500000 = 0,01 mm a jednotným materiálově nelineárním nerezovým materiálem s pracovním diagramem podle obr. 3 umožnila zavést i tření v prokluzu lanových táhel na sedlech. Vyšetřována byla vzpínadla se symetrickým i antisymetrickým tvarem počátečního průhybu. Tření bylo zavedeno v několika velikostech: od nepatrného, odpovídajícího teflonovému povlaku ν = 0,01 až po hodnotu ν = 0,10, odpovídající kontaktu ocel-ocel. Na obr. 13 jsou uvedeny výsledky porovnání největšího dosaženého zatížení (odpovídající kritické síle) pro extrémně nízké tření ν = 0,01, tuhé i kluzné uložení a různé hodnoty předpětí. Je zřejmé, že pro symetrická vybočení se vliv kluzného uložení neprojeví, zatímco u antisymetrických tvarů vybočení může být vliv prokluzu na sedlech značný.
6. Závěr
Článek navazuje na předchozí článek prvního autora o vzpínadlových prutech, jejich kritickém zatížení a skutečné únosnosti [1]. V tomto článku jsou úvodem popsány výsledky 4 testů předpjatých nerezových vzpínadel, sestavených z centrální trubky, čtyřramenného středového kříže a lankových táhel. Následně jsou ukázány teoretické přístupy k určení kritických sil „ideálních“ (přímých) vzpínadlových prutů (lineární bifurkační analýza, analytická metoda a geometricky, popř. i materiálově nelineární analýzy 3D GNIA a 3D GMNIA) a zejména numerické analýzy k určení únosnosti skutečných („imperfektních“) vzpínadel (s amplitudou počátečního průhybu podle ČSN EN 1993-1-1, tj. w0 = L/200) pomocí 3D GNIA a 3D GMNIA. Vyšetřovány byly vlivy velikosti a tvaru počátečních průhybů, směru vybočení centrálního prutu, vlivy materiálové nelinearity a způsob uložení táhel na středovém kříži.
Výsledky umožňují stanovit následující závěry:
- K určení kritické síly vzpínadla v celé šíři různých předpětí táhel je zapotřebí GNIA (popř. GMNIA pro nelineární materiály), se zavedením infinitesimální amplitudy a příslušného tvaru počátečního průhybu centrální trubky, popř. analytická aproximace uvedená v odstavci 3.2.
- Z důvodu „aktivace“ táhel vzpínadla na konvexní straně po vybočení může být skutečná únosnost při malých předpětích vzpínadel (nebo i u vzpínadel nepředpjatých) podstatně vyšší než kritická síla.
- Směr vybočení čtyřramenného vzpínadla, ať ve směru ramen nebo mezi ramena kříže, téměř neovlivňuje velikost kritické síly ani únosnost vzpínadla.
- Vliv tvaru a amplitudy počátečního průhybu w0 na únosnost vzpínadla je podstatný. Ve vyšetřovaném případě činí snížení únosnosti pro skutečné („imperfektní“) vzpínadlo (w0 = L/200) oproti „ideálnímu“ vzpínadlu (w0 = L/500000) 37 % (22,74 kN/36,18 kN = 0,63), u nelineárního nerezového materiálu 38 % (19,57kN/31,58kN = 0,62).
- Materiálová nelinearita (např. při použití nerezových ocelí pro centrální prut a kříž) významně snižuje kritické síly i únosnost vzpínadla. U vyšetřovaného případu činí snížení 14 % (19,57 kN / 22,74 kN = 0,86).
- Tuhost táhel (změna průřezu nebo změna modulu pružnosti) významně ovlivňuje kritické síly i únosnost vzpínadla. U vyšetřovaného případu při změně modulu pružnosti z 200 GPa na 107 GPa činí pokles kritické síly 32 % (27,14 kN / 39,64 kN = 0,68) a pokles únosnosti při optimálním předpětí 27 % (26,84 kN / 36,79 kN = 0,73)
- Významný je způsob uložení táhel na kříži. Projevuje se však pouze u antisymetrického vybočení, kde u kluzného uložení dochází k prokluzu na kříži. Při kluzném uložení s minimálním třením činí u vyšetřovaného případu s materiálovou nelinearitou (GMNIA) pokles kritické síly 21 % (25,12 kN / 31,82 kN = 0,79).
Experimentální a teoretické vyšetřování uvedené v tomto článku je zaměřeno na podrobnější vysvětlení chování předpjatých vzpínadel se zřetelem na kritické síly i únosnost. Doplňuje tak praktická doporučení uvedená v předchozím článku (Macháček [1]). K praktickému návrhu lze použít též přístup podle Tankové a kol. [7]), kde je odvozen přibližný postup pro návrh vzpínadla s jedním křížem jako prutu na vzpěr podle Eurokódu 3. Upozornit lze rovněž na článek Wadeeho a kol. [8], který uvádí numerické řešení vzpínadel ve vodorovné poloze, zatížených osovou silou a vlastní tíhou (lze ovšem namítnout, že tento případ lze snadno řešit zvětšením amplitudy počáteční imperfekce).
7. Oznámení
Článek a související výzkum vznikl za podpory grantu SGS19/150/OHK1/3T/11.
8. Literatura
- Macháček, J.: Předpjaté ocelové tlačené trubky s jedním křížem. TZB-info, ocelové konstrukce, 16. 1. 2019, 10 stran.
https://stavba.tzb-info.cz/ocelove-konstrukce/18519-predpjate-ocelove-tlacene-trubky-s-jednim-krizem - Wadee, M. A., Gardner, L. a Osofero, A. I.: Design of prestressed stayed columns. Journal of Constructional Steel Research, 80, 2013, s. 287–298
https://abdn.pure.elsevier.com/en/publications/design-of-prestressed-stayed-columns - Servítova, K. a Macháček, J.: Analysis of stainless steel stayed columns. Proceedings 6th Intern. Symp. Steel Structures, Korean Society of Steel Construction, Seoul, Nov. 3–5, 2011, s. 874–881.
- Hafez, H. H., Temple M. C. a Ellis, J. S.: Pretensioning of single-crossarm stayed columns. Journal of the Structural Division ASCE, ST2, Feb. 1979, s. 359–375.
- Smith, R. J., McCaffrey G. T., a Ellis J. S.: Buckling of a single-crossarm stayed column. Journal of the Structural Division ASCE, 11071, ST1, Jan. 1975, s. 249–268.
- Píchal, R. a Macháček, J.: Stability of stainless steel prestressed stayed columns. Proc. 21st Int. Conf. Engineering Mechanics 2015, eds. J. Náprstek and C. Fischer, Svratka, 2015, s. 230–231.
- Pichal, R. a Machacek, J.: Buckling and post-buckling of prestressed stainless steel stayed columns. Engineering Structures and Technologies, Vol. 9, No. 2, 2017, s. 63–69
https://journals.vgtu.lt/index.php/EST/article/view/600 - Tankova, T., Simões da Silva, L., Martins J. P.: Stability design of cable-stayed columns. Intern. Colloq. on Stability and Ductility of Steel Structures (SDSS 2019), Eds. F. Wald and M. Jandera, 2019, s. 888–905.
https://online.vitalsource.com/#/books/9781000752243/ - Wadee, M. A., Wu, K., Gardner, L.: Interactive buckling in prestressed stayed beam-columns. Intern. Journal of Mechanical Sciences, Vol. 174, 2020
https://www.sciencedirect.com/science/article/abs/pii/S0020740319347435?via%3Dihub
Article follows the previous general treatise concerning prestressed steel compression tubes with just one crossarm (Machacek [1]). This article deals with tests of stayed columns, numerical analyses and their evaluation. In the theoretical part the linear bifurcation analysis (2D LBA) to establish critical loads and buckling modes is presented, the geometrically nonlinear analysis to establish strengths of imperfect stayed columns (3D GNIA) and also the geometrically and materially nonlinear analysis to establish strengths of imperfect stayed columns made of stainless steels (3D GMNIA) are introduced. Numerical calculations employ software ANSYS and are validated by tests. Parametrically are investigated impacts of initial deflections, directions of buckling, material nonlinearities and the technique of the stays supports at crossarms. Results are summarized into practical recommendations.