Předpjatá trubková ocelová vzpínadla se dvěma kříži
Článek navazuje na předchozí pojednání o předpjatých ocelových trubkách pouze s jedním křížem (Macháček a Píchal [13]). Vyšetřováno je vzpínadlo se dvěma kříži, zatímco ostatní parametry jsou shodné s testovaným a analyzovaným vzpínadlem s jedním centrálním křížem. Pro kritické zatížení a rozhodující tvary při vybočení nepředpjatého vzpínadla se uvádí lineární bifurkace. Pro předpjaté vzpínadlo je odvozeno analytické řešení, umožňující stanovit kritické zatížení pro libovolné předpětí, včetně optimálního předpětí ke stanovení maximální kritické síly. Hlavní studie uvádí geometricky, popř. i materiálově nelineární řešení s imperfekcemi v prostředí ANSYS. Ukazuje potřebu nelineárního řešení i pro stanovení kritického zatížení "ideálního" vzpínadla, zatímco pro stanovení únosnosti "imperfektního" vzpínadla, s příslušným počátečním průhybem, je zcela nezbytné. V závěru je analyzován vliv materiálové nelinearity i počtu křížů, s doporučeními pro návrh vzpínadel.
1. Úvod
Předpjaté ocelové prvky nacházejí stále širší uplatnění, neboť jejich předpínací prvky (tyče nebo lana z ocelí vysoké pevnosti) i napínací mechanizmy se staly běžně dostupné. Jejich použitím lze navrhnout štíhlé a subtilní konstrukce s vysokou únosností i estetickou hodnotou. Rozvoj předpjatých ocelových prvků od historických počátků (Ferjenčík a Tocháček [1]) dospěl v posledním období do sofistikovaných předpjatých konstrukcí vazníků, velkorozponových konstrukcí i mostů (Janata [2], [3]). V oblasti výzkumu je velká pozornost věnována vzpínadlovým předpjatým prvkům, jejichž chování z hlediska kritických sil a únosnosti je věnována celá řada experimentálních, analytických i numerických studií (např. Hafez [4], Chan a kol. [5], Araujo a kol. [6], Saito a kol. [7], Wadee a kol. [8], Servítová a Macháček [9], Osofero a kol. [10], Píchal a Macháček [11] a další).
Základní informace k tlačeným předpjatým vzpínadlům jsou uvedeny v článku prvního autora (Macháček [12]), který obsahuje informace o stabilitě vzpínadel, analytickém stanovení kritického zatížení a optimálního předpětí a také doporučení ke stanovení únosnosti pro „imperfektní“ vzpínadla (s různým počátečním průhybem). Uveden je i číselný příklad posouzení vzpínadla z austenitické oceli a lanovými táhly. Další článek (Macháček a Píchal [13]) se zabývá předpjatými vzpínadly s jedním centrálním křížem a je zaměřen na experimenty, analytické řešení a numerické analýzy (lineární bifurkaci 2D LBA, geometricky nelineární analýzy s imperfekcemi 3D GNIA, popř. i materiálovou nelinearitou 3D GMNIA). Z výsledků příslušných parametrických studií vyplývají závěry a doporučení pro návrh těchto vzpínadel.
Při návrhu je nutné rozlišovat ztrátu stability „ideálního“ (dokonale přímého) prutu při dosažení kritického zatížení, únosnost skutečného („imperfektního“) prutu dosažené při jeho kolapsu, popř. návrhové únosnosti podle návrhových norem. Tyto pojmy a obecné možnosti uspořádání vzpínadlových prutů a křížů uvádí podrobněji předchozí článek (Macháček [12]). Větší počet příčných křížů byl mnohokrát aplikován v praxi (viz např. obr. 1), neboť umožňuje další zvýšení štíhlosti a vyšší únosnost při srovnání s tlačeným vzpínadlem s jedním centrálním křížem.
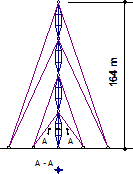
Obr. 1 Stožár z roku 1955 v Rusku (vlevo), Chiswick Park v Londýně (uprostřed), Estádio Algarve ve Faru (vpravo)
Tento návazný článek se zaměřuje na přístupy k řešení stability a únosnosti vzpínadlových prutů se dvěma kříži umístěnými ve třetinách délky centrálního prutu. Kromě návrhu analytického řešení kritických sil se věnuje numerickým metodám, které byly validovány na experimentech v předchozím článku (Macháček a Píchal [13]). Parametrické studie se zabývají vyhodnocením efektivity z různých hledisek (vlivu velikosti a tvaru počátečních průhybů, velikosti předpětí, podle použitého materiálu trubek a podle počtu křížů).
2. Parametry vyšetřovaných vzpínadel
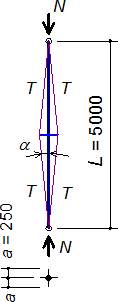
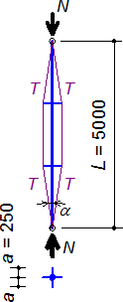
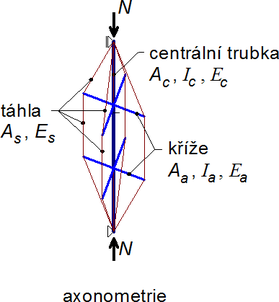
Základní geometrie vyšetřovaných vzpínadel vychází ze vzorků testovaných v laboratoři Fakulty stavební ČVUT (Servítová a Macháček [9]), na nichž kromě testů byly validovány numerické modely a podrobně vyšetřována vzpínadla s jedním centrálním křížem (Macháček a Píchal [13]). Vzpínadlový prut tvoří centrální trubka namáhaná tlakem N, dva kříže z trubek se čtyřmi rameny v úhlu 90º a táhla, každé pro vnesení předpětí T. Shrnutí hlavních parametrů, kde vzpínadla se dvěma kříži se liší od zkoušených v laboratoři pouze počtem křížů a tyčovými táhly místo lanek (obr. 2):
- Centrální trubka: Ø 50×2 [mm], nerezová ocel 1.4301 (L = 5000 mm, Ac = 302 mm2, Ic = 87009 mm4).
- Kříž: Ø 25×1,5 [mm], nerezová ocel 1.4301 (a = 250 mm, Aa = 111 mm2, Ia = 7676 mm4).
- Tyčová táhla Ø 4 mm, nerezová ocel 1.4301 (Ls = 2513 mm, As = 12.6 mm2).
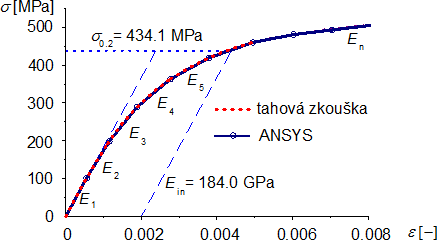
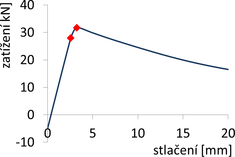
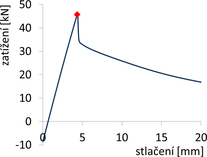
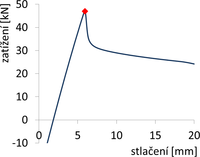
Modul pružnosti nerezové oceli byl pro následné vyšetřování uvažován podle ČSN EN 1993-1-4 v konstantní hodnotě E = 200 GPa. Pro materiálově nelineární analýzy byl zaveden pracovní diagram zjištěný pro testovaná vzpínadla z tahových vzorků s průřezem celých trubek (viz Macháček a Píchal [13]). Pracovní diagram získaný ze zkoušek 3 vzorků a polygonální aproximace pro numerické řešení v softwaru ANSYS je zobrazena na obr. 3.
3. Teoretické vyšetřování
3.1 Lineární bifurkace nepředpjatého vzpínadlového prutu se dvěma kříži
K řešení lineární pružné stability nepředpjatého vzpínadlového prutu Ncr,T=0 lze použít jednoduchou bifurkační analýzu (2D LBA), obdobně jako pro vzpínadla s jedním centrálním křížem. Jednoduchá analýza daného vzpínadla ve 2D softwarem Scia Engineer poskytla výsledky podle obr. 4. Ukázány jsou výsledky pro první tři tvary vybočení a odpovídající kritické síly. Modul pružnosti všech částí byl zaveden zjednodušeně jednotně hodnotou E = 200 GPa.
Tyto výsledky mají význam pro stanovení tvaru imperfekcí u nelineárních analýz a rovněž jsou dále použity při odvození analytického vyjádření kritických sil předpjatých vzpínadel. Pro předpjaté vzpínadlové pruty je nutné jak pro kritické hodnoty, tak pro maximální únosnosti použít geometricky nelineární analýzu s imperfekcemi (GNIA), neboť při vybočení dochází k náhlým změnám vnitřní energie prutové soustavy, které LBA nepostihuje. Pouze pro ilustraci jsou též uvedeny hodnoty pro stejná táhla, ale probíhající spojitě přes oba kříže, kde jsou kluzně uloženy na sedlech (viz Macháček a Píchal [13]).
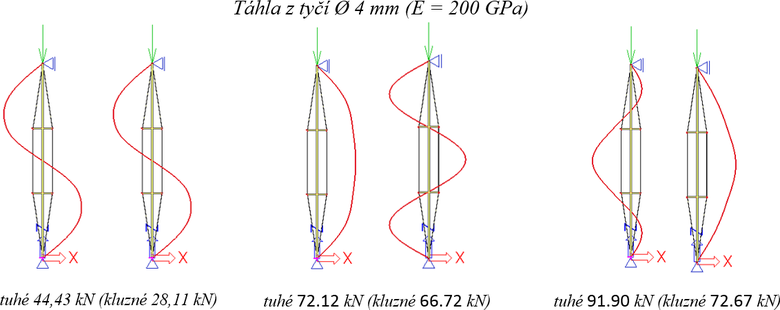
Obr. 4 První tři kritické síly Ncr,T=0 a tvary vybočení podle LBA pro tuhé i kluzné uložení táhel na křížích
Z porovnání je zřejmé, že kluzné uložení může výrazně snížit kritickou sílu, popř. i tvar vybočení. Podobný závěr vyplynul i z vyšetřování vzpínadel s jedním centrálním křížem (Macháček a Píchal [13]).
3.2 Analytická aproximace kritického zatížení předpjatého vzpínadlového prutu
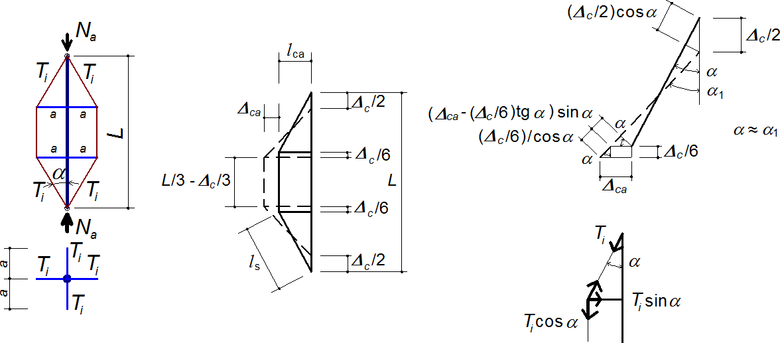
Odvození kritického zatížení „ideálního“ vzpínadlového prutu s jedním křížem uprostřed délky pro libovolné předpětí je podrobně, včetně numerického příkladu, uvedeno v [12] (původní odvození publikovali Hafez a kol. [4]). Obdobně je dále odvozeno pro dva kříže ve třetinách délky vzpínadlového prutu. Pro odvození platí stejné předpoklady: Prut je ideálně přímý, kloubově uložený, bez imperfekcí, přípoje křížů k prutu jsou tuhé, všechny přípoje táhel jsou kloubové, osová deformace křížů je zanedbána. Z obr. 5 plyne:
Dále, včetně symboliky použité v [12], platí pro počáteční osovou sílu po předpětí Ni, celkovou sílu po aplikaci zatížení Nf, pro tuhosti prutu Kc, křížů Kca, táhel Ks a stlačení jednotlivých částí:
Ve vztazích odpovídá počet táhel n = 4 pro řešení ve 3D, n = 2 pro řešení ve 2D. Odtud po dosazení a sloučení plynou pro pokles tahu v táhlech (Ti − Tf), výsledný tah v táhlech Tf a vnější zatížení Na vztahy:
Tyto vztahy mají stejný význam jako pro případ předpjatého vzpínadla s jedním křížem. Analýza vede opět ke třem zónám chování vzpínadlového prutu, podle velikosti předpětí (obr. 6).
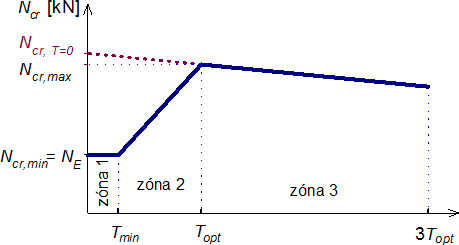
Obr. 6 Idealizovaný diagram kritického napětí Ncr vzpínadel se dvěma kříži pro různá předpětí táhel T
Zóna 1 – Předpětí je nízké (Tf ≤ Tmin):
Počáteční předpětí v prutu po zatížení vymizí a prut se chová jako bez táhel. Pro Eulerovu kritickou sílu až do minimálního předpětí Tmin ze vztahu (9) plyne:
Pozn.: Pro prostorové uspořádání (4 táhla) n = 4, pro rovinné uspořádání (2 táhla) n = 2.
Zóna 2 – Počáteční předpětí je větší než minimální, ale menší než optimální (Tmin < Tf < Topt):
Po vybočení předpětí v táhlech vymizí (Tf = 0), avšak na konvexní straně vybočení se okamžitě aktivuje. Výsledná kritická síla je větší než Eulerova. Ze vztahu (9) plyne:
Maximální kritická síla plyne ze vztahu (12) po dosazení Na = Ncr,n,T=0, kde kritická síla pro nulové předpětí plyne z LBA (viz obr. 6):
Odpovídající „optimální“ předpětí je potom:
Zóna 3 – Počáteční předpětí je větší než optimální (Tf ≥ Topt):
V tomto případě zůstávají táhla po vybočení aktivní (napjatá). Účinek předpětí v táhlech zvyšuje zatížení, a tím snižuje kritické napětí prutu.
Reziduální tah v táhlech plyne ze vztahů (11) a (17):
kde konstanta C3 je:
Kritická síla v zóně 3 potom plyne ze vztahu (19) po zavedení Na = Ncr a Nf = Ncr,max :
Důležitá poznámka:
Při tomto odvození není zohledněn fakt, že u vzpínadel se dvěma kříži může dojít po vybočení ke změně původního předpokládaného tvaru. Oproti vzpínadlům s jedním křížem dává proto analytické řešení pouze přibližné hodnoty kritických břemen a optimálních předpětí. Pro charakteristiky prutu, křížů a táhel podle kap. 2 (testovaná vzpínadla s jedním křížem), avšak s jednotným modulem pružnosti E = 200 GPa vychází:
- Ncr,1,T=0 = 44,43 kN (viz obr. 4 pro dva příčné kříže);
- NE = 6870 N;
- Tmin = 241 N;
- Ncr,max = 38262 N;
- Topt = 1343 N;
- Ncr,3Topt = 25925 N.
Získaná maximální kritická síla Ncr,max = 38262 N je velmi blízká hodnotě z numerického řešení GNIA (viz následující kap. 4.1), která odpovídá splynutí kritické a maximální síly Ncr = 38200 N. Optimální předpětí z analytického řešení Topt = 1343 N je však nižší než ukazuje numerická analýza (Topt = 1661 N). Průběh kritických sil z nelineárního řešení (obr. 7 a obr. 8) jasně ukazuje, že analytické řešení nemůže dávat realistické hodnoty pro různá předpětí, nicméně poskytuje praktickou orientační hodnotu kritické síly.
4. Nelineární numerická analýza ve 3D
Nelineární analýza byla provedena v softwaru ANSYS. Pro centrální trubku a kříže byly použity prutové elementy BEAM188 a pro táhla prvek LINK188 (s volbou aktivní jen pro tah), kloubově připojenými ke konci centrální trubky. Všechny uvedené konečné prvky disponují velkými deformacemi a plasticitou, umožňující řešení geometricky a materiálově nelineární analýzou s imperfekcemi (GMNIA). Optimalizace sítí konečných prvků vedla k osovému dělení pro centrální trubku na L / 250 a ramen křížů na a / 25 (viz obr. 2).
Po zavedení požadovaných počátečních průhybů bylo předpětí docíleno ochlazením táhel. Pro testovaná vzpínadla bylo aplikováno ochlazení na dané předpětí, pro parametrické studie obvykle pro 30 teplotních hodnot, pokrývajících požadované spektrum předpětí. Ochlazení z pokojové na danou teplotu bylo vždy provedeno v 10 krocích k obnovení rovnováhy na deformovaném vzpínadle a poté bylo aplikováno vnější zatížení na centrální prut. Pro každý stupeň zatížení se použila Newton-Raphsonova iterace (N-R) s limitem 1000 iterací, popř. do splnění konvergenčního limitu.
Validace numerické analýzy GMNIA byla úspěšně provedena pro všechna testovaná vzpínadla s jedním centrálním křížem (Macháček a Píchal [13]).
Studie vzpínadel se dvěma kříži jsou uspořádány obdobně jako předchozí studie vzpínadel s jedním křížem. Pro řešení kritických zatížení „ideálních“ vzpínadel i skutečné únosnosti „imperfektních“ vzpínadel v celém rozsahu předpětí je opět nutné použít nelineární geometrickou analýzu, neboť při aplikaci předpětí (zejména v zóně 2, popř. při přeskocích tvarů vybočení) dochází k náhlé změně vnitřní energie prutu, které LBA nemůže postihnout.
Kritické zatížení vzpínadla (tj. pro „ideální“ přímý prut), proto vyžaduje geometricky nelineární řešení s „infinitesimální“ (téměř nulovou) velikostí počátečního průhybu, jehož hodnota byla zvolena v obou směrech ramen kříže w0y = w0z = L / 500000 = 0,01 mm.
Reálná únosnost vzpínadla (tj. pro „imperfektní“, počátečně zakřivený prut), byla řešena pro počáteční průhyb požadovaný Eurokódem ČSN EN 1993-1-1 pro za studena tvarované trubky řešené pružnou analýzou s tím, že hodnota tohoto průhybu mezi rameny kříže (v prostoru) je w0 = L / 200 = 25,0 mm.
Řešení 3D GNIA (pro nerezové trubky 3D GMNIA) v celém rozsahu možných předpětí vyžaduje pro každé předpětí (řádově 30–40 hodnot) volit vhodné stupně vnějšího zatížení (řádově 1000 stupňů) a pro každý stupeň značné množství N-R iterací. Výpočty proto vyžadovaly výkonný počítač a značný výpočetní čas. Detailní řešení bylo proto provedeno pouze pro geometrické charakteristiky vzpínadel uvedené v kap. 2 (centrální trubka Ø 50×2 [mm], ramena kříže Ø 25×1,5 [mm], táhla Ø 4 mm), obr. 2.
4.1 Numerické řešení vzpínadel se dvěma kříži ve 3D GNIA
Pro všechny části vzpínadla z nerezové oceli byl zjednodušeně zaveden jednotný materiál s konstantním modulem pružnosti nerezové oceli E = 200 GPa a výše uvedené amplitudy počátečních průhybů. Pro antisymetrický tvar počátečních průhybů a celé spektrum předpětí jsou výsledky uvedeny na obr. 7 a pro symetrický tvar počátečních průhybů na obr. 8.
Z LBA (obr. 4) vyplývá, že rozhodující tvar vybočení pro vyšetřované vzpínadlo je antisymetrický. Při řešení GNIA toto vybočení převládne dokonce i pro infinitesimální symetrický počáteční průhyb w0 = L / 500000, takže ve výsledku je kritické zatížení pro oba počáteční tvary identické pro libovolné předpětí (tečkované průběhy na obr. 7 a 8). Pro nízká předpětí jsou uvedeny dvě křivky chování „ideálního“ vzpínadla: Vlastní kritické zatížení indikuje vybočení centrální trubky, kdy se táhla na konkávní straně vybočení uvolní (jsou bez napětí). V témže okamžiku se však aktivují táhla na konvexní straně, což vede ke schopnosti vzpínadla přenášet další zatížení, resp. k únosnosti „ideálního“ vzpínadla. Podrobný rozbor, včetně velikosti sil v jednotlivých táhlech při různém předpětí je ukázán v kap. 4.2 (GMNIA).
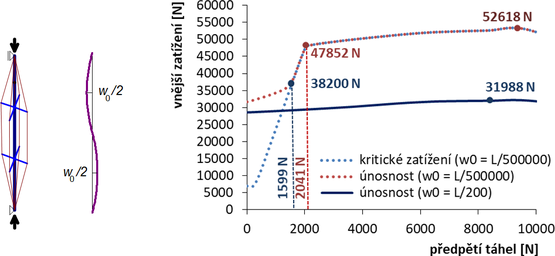
Obr. 7 Výsledky 3D GNIA, antisymetrické počáteční průhyby. Závislost kritického zatížení a únosnosti na předpětí táhel
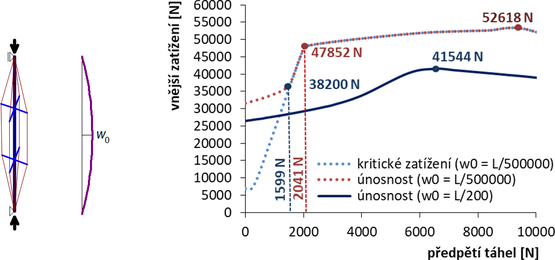
Obr. 8 Výsledky 3D GNIA, symetrické počáteční průhyby. Závislost kritického zatížení a únosnosti na předpětí táhel
Z porovnání únosností „imperfektního“ vzpínadla, pro w0 = L / 200 (plné čáry na obr. 7 a 8) je zřejmé, že antisymetrický tvar vybočení rozhoduje, dává podstatně nižší únosnosti než symetrický tvar, přičemž velikost předpětí nehraje významnou úlohu. Únosnost „imperfektního“ vzpínadla je samozřejmě v celém rozsahu předpětí nižší než únosnost „ideálního“ vzpínadla (nicméně pro malá předpětí vyšší než klasická kritická síla).
4.2 Numerické řešení vzpínadel se dvěma kříži ve 3D GMNIA
Pro všechny části vzpínadla z nerezové oceli byl zaveden jednotný materiál s pracovním diagramem podle obr. 3. Pro antisymetrický tvar počátečních průhybů a celé spektrum předpětí jsou výsledky uvedeny na obr. 9 a pro symetrický tvar počátečních průhybů na obr. 10.
Komentář k průběhu kritického zatížení i únosnosti pro oba typy tvarů počátečních průhybů je podobný k řešení GNIA (kap. 4.1). Rozdíl se však projevuje i u kritického zatížení, kde rozhodující infinitesimální antisymetrický počáteční průhyb dává poněkud nižší hodnoty než symetrický počáteční průhyb. Je to způsobeno nižším a proměnlivým modulem pružnosti pro danou velikost zatížení a předpětí. Únosnost pro nelineární materiál (GMNIA) je podstatně nižší než dává řešení pro lineární materiál (GNIA).
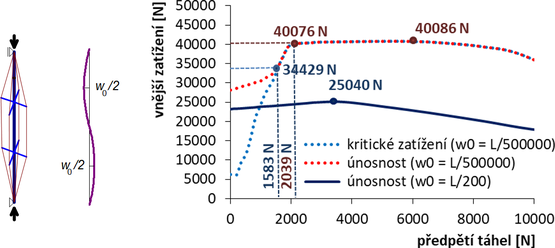
Obr. 9 Výsledky 3D GMNIA, antisymetrické počáteční průhyby. Závislost kritického zatížení a únosnosti na předpětí táhel
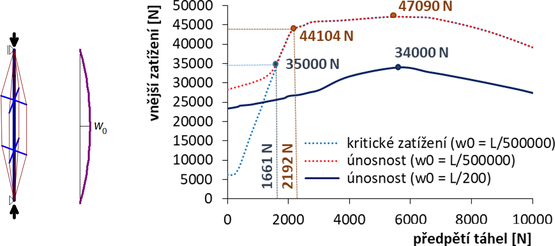
Obr. 10 Výsledky 3D GMNIA, symetrické počáteční průhyby. Závislost kritického zatížení a únosnosti na předpětí táhel
Pro „ideální“ vzpínadlo lze opět pro nízká předpětí pozorovat vyšší únosnost než kritickou sílu. Vysvětlení mechanizmu uvolnění táhel při dosažení kritické síly na konkávní straně vzpínadla a napnutí táhel na konvexní straně pro dosažení únosnosti je vysvětleno na obr. 11.
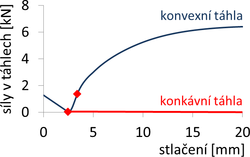
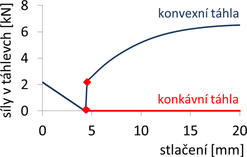
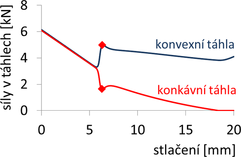
Obr. 11 Závislost sil v táhlech na stlačení centrální trubky vzpínadla: A – malé předpětí (T = 1278 N), B – střední předpětí (T = 2192 N), C – velké předpětí (T = 6149 N)
Při malých předpětích (případ A) se táhla při vybočení (tj. dosažení kritické síly) na konkávní straně vzpínadla uvolní a na konvexní straně aktivují, takže lze dosáhnout vyšší konečné únosnosti než je kritická hodnota. Pro střední velikost předpětí (případ B) se při vybočení táhla na konkávní straně uvolní a na konvexní straně aktivují, avšak vzpínadlo vybočuje a vyšší únosnosti se již nedosáhne. Podobně je tomu při velkých předpětích (případ C), kde však po vybočení zůstávají všechna táhla (i na konkávní straně) aktivní.
5. Závěr
Tento článek navazuje na předchozí základní pojednání o předpjatých vzpínadlech prvního autora [12] a článek o trubkových vzpínadlech s jedním křížem obou autorů [13]. V tomto pokračování se uvádí teoretické řešení předpjatých trubkových vzpínadel se dvěma kříži. K jednoduchému řešení kritické síly "ideálního" (dokonale přímého) nepředpjatého vzpínadla je použita lineární bifurkační analýza (2D LBA). Pro předpjaté vzpínadlo je dále odvozeno analytické řešení kritické síly, které obdobně jako pro vzpínadla s jedním křížem umožňuje stanovit optimální předpětí ke stanovení maximální hodnoty kritické síly.
Ke stanovení únosnosti imperfektního vzpínadla (s libovolnou počáteční deformací) je navrženo řešení geometricky nelineární analýzou s imperfekcemi (GNIA), případně i se zahrnutím materiálové nelinearity (GMNIA) v softwaru ANSYS. Pro předpjatá vzpínadla může docházet při vybočení k náhlé změně vnitřní energie, které lineární řešení (LBA) nepostihuje a proto i pro kritické zatížení je nutné použít GNIA (GMNIA), s velmi malým (infinitesimálním) počáteční průhybem. Nelineární analýzy byly proto použity jak pro stanovení kritických sil předpjatého „ideálního“ vzpínadla (s amplitudou počátečního průhybu w0 = L / 500000), tak pro stanovení únosnosti skutečného „imperfektního“ vzpínadla (s amplitudou w0 = L / 200).
Studie v článku pokrývají pouze geometrii vzpínadla použitého v laboratoři a zkoumaného též pro vzpínadla s jedním křížem (obr. 2). Nicméně, získané výsledky lze zobecnit do následujících závěrů a doporučení pro vzpínadla se dvěma čtyřramennými kříži:
- K získání kritického zatížení předpjatého vzpínadla pro dané předpětí je nutné použít geometricky nelineární analýzu (GNIA nebo GMNIA) s příslušným tvarem počáteční deformace a infinitesimální amplitudou.
- Vzhledem k aktivaci táhel po vybočení na konvexní straně je únosnost i „ideálního“ vzpínadla s velmi malým předpětím vyšší než jeho kritické zatížení.
- Nelineární materiál vzpínadla (např. nerezová ocel podle obr. 3) významně snižuje jak kritické zatížení, tak únosnost vzpínadla ve srovnání s pružným materiálem pro E = 200 GPa. Snížení únosnosti u vyšetřovaného vzpínadla činí 22 % (25040 N / 31988 N = 0,78).
- Analytické řešení kritického zatížení pro vzpínadla se dvěma kříži nemůže poskytnout hodnověrné výsledky v celém rozsahu předpětí, neboť nepostihuje změny tvarů vybočení. Nicméně, dává orientační konzervativní hodnoty pro optimální předpětí a příslušnou kritickou sílu.
- Přidáním druhého kříže k jinak zcela stejnému vzpínadlu s jedním křížem (viz článek Macháček a Píchal [13]) podstatně zvyšuje jak kritické zatížení, tak únosnost. Např. pro nerezový materiál ve vyšetřovaném případě činí zvýšení kritické síly 27 % (40086 N / 31580 N) a únosnosti o 28 % (25040 N / 19570 N), pro lineární materiál dokonce 45 % (52618 N / 36180 N), resp. 41 % (31988 N / 22740 N).
Z vyhodnocení výsledků získaných pro vzpínadla s jedním a dvěma kříži vyplývá, že návrh vzpínadla vyžaduje vhodný předběžný odhad geometrických a materiálových parametrů, neboť materiál i tuhosti jednotlivých prvků, zvláště táhel, výrazně ovlivňují chování při vybočení a únosnost vzpínadla. K odhadu může sloužit kombinace LBA a analytického řešení, popř. přibližné vztahy odvozené z parametrických studií (např. [8], uvedené v [12]). Skutečnou únosnost a vhodné předpětí je potom nutné řešit nelineárním výpočtem (GNIA, popř. GMNIA).
6. Oznámení
Článek a související výzkum vznikl za podpory grantu SGS19/150/OHK1/3T/11.
7. Literatura
- Ferjenčík, P., Tocháček, M.: Predpäté kovové konštrukcie. Slovenské vyd. technické literatúry, Bratislava, 1966, 298 s.
- Janata, V.: Předpjaté ocelové konstrukce. Příloha Konstrukce, 6/2010, 6 s.
- Janata, V.: Předpjaté ocelové konstrukce. Technologie, ekonomika, nová konstrukční schémata. Konference Ocelové konstrukce ve službách architektury, Excon a.s., 2018, PPP, 54 s.
https://ocelvarchitekture.cz/prednasky/Ocelvarch_Excon_Janata_Predpajte_ocelove_konstrukce.pdf - Hafez, H. H., Temple, M. C. a Ellis, J. S.: Pretensioning of single-crossarm stayed columns. J. Struct. Div. ASCE, 14362, ST2, 1979, s. 359–75.
- Chan, S. L., Shu, G. a Lü, Z.: Stability analysis and parametric study of pre-stressed stayed columns. Eng. Struct. 24(1), 2002, s. 115–124.
- Araujo, R. R., Andrade, S. A. L., Vellasco, P. C. G. S., Silva, J. G. S. a Lima, L. R. O.: Experimental and numerical assessment of stayed steel columns. J. Constr. Steel Research 64(9), 2008, 1020–1029.
- Saito, D. a Wadee, M. A.: Numerical studies of interactive buckling in prestressed steel stayed columns. Eng. Struct. 31(2), 2009, s. 432–443.
https://www.sciencedirect.com/science/article/abs/pii/S0141029608003088 - Wadee, M. A., Gardner, L., Osofero, A. I.: Design of prestressed stayed columns. Journal of Constructional Steel Reesearch, 80, 2013, s. 287–298.
https://abdn.pure.elsevier.com/en/publications/design-of-prestressed-stayed-columns - Servítova, K., Macháček, J.: Analysis of stainless steel stayed columns. Proceedings 6th Intern. Symp. Steel Structures, Korean Society of Steel Construction, Seoul, Nov. 3-5, 2011, s. 874–881.
- Osofero, A. I., Wadee, M. A. a Gardner, L.: Experimental study of critical and post-buckling behaviour of prestressed stayed steel columns. J. Constr. Steel Research 79, 2012, s. 226–241.
https://www.sciencedirect.com/science/article/pii/S0143974X12001708 - Pichal, R. a Machacek, J.: Stability of stainless steel prestressed stayed columns. Proc. 21st Intern. Conf. Engineering Mechanics 2015, Svratka, 2015, s. 230–231.
https://www.engmech.cz/improc/2015/EA_Pichal_048.pdf - Macháček, J.: Předpjaté ocelové tlačené trubky s jedním křížem. TZB-info, ocelové konstrukce, 16. 1. 2019, 10 stran.
https://stavba.tzb-info.cz/ocelove-konstrukce/18519-predpjate-ocelove-tlacene-trubky-s-jednim-krizem - Macháček, J. a Píchal, R.: Předpjatá trubková ocelová vzpínadla s jedním křížem. TZB-info, ocelové konstrukce, v tisku.
Article follows the previous treatise concerning prestressed steel tubes with just one crossarm (Machacek a Pichal [13]). A stayed column with two crossarms is investigated, while other parameters as those of tested and analysed stayed columns with one crossarm are identical. Critical loadings and decisive buckling modes of unprestressed stayed columns are solved by linear bifurcation. For prestressed stayed columns the analytical method is derived, which enables calculation of critical loading under an arbitrary prestress including the optimal one, resulting into maximal critical loading. The main study introduces geometrically, possibly also materially nonlinear analyses with initial imperfections, using software ANSYS. The nonlinear analysis is shown to be necessary even for critical loading of "ideal" stayed column, while for strength of "imperfect" stayed column, with given initial deflection, is absolutely essential. Finally are analysed impacts of material nonlinearity and numbers of crossarms, followed by practical design recommendations.