Vylévání ocelových sloupků betonem
Příspěvek se zabývá problematikou vylévání ocelových sloupů betonem a otázkou, jak se projeví rozdílnost součinitelů příčné kontrakce obou materiálů. Přestože se na první pohled, pro případ prostého tlaku, zdá být úloha zcela banální, mohou prezentované skutečnosti svým způsobem překvapit. Za pozornost určitě stojí nezanedbatelné tahové napětí kolmo na osu betonové výplně.
1. Úvod
K napsání tohoto příspěvku vedla otázka, jaké napětí vznikne na vnitřním povrchu ocelové trubky vylité betonem. Trubka v konstrukci funguje jako sloup a pro jednoduchost uvažujeme, že nastane případ prostého tlaku. Je všeobecně známo, že součinitel příčné kontrakce oceli je větší než součinitel příčné kontrakce betonu, a to by se mělo v namáhání trubky vylité betonem nějak projevit. I když se ve výuce předmětu Pružnost a pevnost toto přímo detailně neprobírá, dává se v předmětu návod, jak danou otázku řešit. V deformační variantě řešení problému matematické teorie pružnosti se říká, že neznámé složky vektoru pole posunutí vyřešíme na základě známých rovnic rovnováhy. K těm se dostaneme přes rovnice geometrické a fyzikální. Při malých deformacích dávají geometrické rovnice návod na výpočet tenzoru malých deformací. Fyzikální rovnice pro izotropní lineárně pružné těleso známe jako zobecnělý Hookeův zákon se dvěma materiálovými parametry, Youngovým modulem pružnosti a součinitelem příčné kontrakce. Fatální otázkou je technický odhad či zjednodušení hledaného pole posunutí. V případě trubky je asi nabíledni řešit úlohu v cylindrických souřadnicích. Za následující kapitolu se všem inženýrům praxe omlouváme, leč přesto si myslíme, že bez této teorie bychom byli nejen ochuzeni, ale navíc bychom na zadanou otázku nedokázali odpovědět.
2. Trocha nevyhnutelné teorie
Hledejme rovnovážné pole posunutí homogenního izotropního lineárně pružného tělesa, které je vzhledem k válcovým souřadnicím (r, φ, z) zatíženo tak, že platí:
kde a, b jsou neznámé konstanty.
Geometrické rovnice v polárních souřadnicích mají tvar
Dosadíme-li do rovnic (2) vztahy (1) a označíme-li parciální derivace podle r čárkou ![]() , obdržíme
, obdržíme
Fyzikální vlastnosti vyjadřují rovnicemi homogenního izotropního lineárně pružného kontinua, které zapíšeme ve tvaru
kde ![]() jsou dvě nezávislé materiálové konstanty.
jsou dvě nezávislé materiálové konstanty.
Pomocí rovnic (3), (4) určíme složky tenzoru napětí v závislosti na posunutí
Složky tenzoru napětí jsou vzájemně svázány třemi rovnicemi rovnováhy, které při zanedbání objemových sil mají v polárních souřadnicích tvar
Požadavky rovnováhy tedy vyjadřují dvě obyčejné diferenciální rovnice
Rovnosti (7) až (8) představují tzv. Eulerovy diferenciální rovnice, k jejichž řešení použijeme substituci
a vztahů
Označíme-li ![]() , získají rovnice (9), (10) podobu
, získají rovnice (9), (10) podobu
Odtud ihned obdržíme
Zpětným dosazením získáme složky tenzoru napětí, jehož složky jsou á priori v rovnováze.
Pro úplnost připomínáme, že v průběhu řešení se nám objevily integrační konstanty ![]() ,
, ![]() a pro popis deformace jsme zavedli neznámý parametr
a pro popis deformace jsme zavedli neznámý parametr ![]() popisující poměrnou deformaci ve směru osy sloupu. Celkem dle očekávání vidíme, že při prostém tahu je napjatost ve sloupu hlavní. Teď už jen zbývá pro konkrétní případy zatížení dořešit neznámé konstanty. Více podrobností k teorii nalezneme v [1] a [2].
popisující poměrnou deformaci ve směru osy sloupu. Celkem dle očekávání vidíme, že při prostém tahu je napjatost ve sloupu hlavní. Teď už jen zbývá pro konkrétní případy zatížení dořešit neznámé konstanty. Více podrobností k teorii nalezneme v [1] a [2].
3. Jednoduché příklady užití v praxi
Nechť ocelový sloup, jehož průřez je mezikruží, je tlačen konstantní silou. Potom se vyvodí konstantní záporná svislá deformace ![]() . Youngův modul pružnosti uvažujeme
. Youngův modul pružnosti uvažujeme ![]() a Poissonův součinitel
a Poissonův součinitel ![]() . Pro ilustraci např.
. Pro ilustraci např. ![]() . Vnitřní a vnější poloměr sloupu jsou známé, např.
. Vnitřní a vnější poloměr sloupu jsou známé, např. ![]() .
.
Dané úloze odpovídají okrajové podmínky
Dosazením do (13), získáme pro integrační konstanty
Snadno nahlédneme, že u tlačeného sloupu dochází k radiálnímu kladnému posunutí na obou lících, a tento je úměrný součiniteli příčné kontrakce daného materiálu
Číselně na vnitřním a vnějším okraji
Tomuto odpovídá napjatost
Výsledek je relativně triviální a odpovídá očekávání. Nevím, zda všichni uhádli, že radiální posun na vnitřním a vnějším líci bude stejně orientován!? Vzhledem ke geometrii úlohy je vidět, že translace elementu trubky ![]() je větší než vliv příčné kontrakce po tloušťce.
je větší než vliv příčné kontrakce po tloušťce.
Řešme ten samý ocelový sloup, jehož průřez je mezikruží, je opět tlačen konstantní silou, ale navíc je vylit betonem. Nechť zatížení vyvodí stejnou konstantní zápornou svislou deformaci ![]() . Youngův modul pružnosti oceli uvažujeme
. Youngův modul pružnosti oceli uvažujeme ![]() a Poissonův součinitel
a Poissonův součinitel ![]() , stejně jako v předchozí úloze. Pro beton jsme zvolili parametry
, stejně jako v předchozí úloze. Pro beton jsme zvolili parametry ![]() a
a ![]() . Opět uvažujeme, že zatížení vyvodí poměrnou deformaci
. Opět uvažujeme, že zatížení vyvodí poměrnou deformaci ![]() . Vnitřní a vnější poloměr sloupu jsme zachovali
. Vnitřní a vnější poloměr sloupu jsme zachovali ![]() . Na kontaktu ocel beton předpokládáme, že se přenáší napětí a je spojité posunutí.
. Na kontaktu ocel beton předpokládáme, že se přenáší napětí a je spojité posunutí.
Dané úloze odpovídají okrajové podmínky
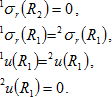
Horní levý index 1 přísluší oceli, a tedy dosazujeme parametry oceli, a stejně činíme i pro beton, jemuž přísluší horní levý index 2. Dosazením do rovnic (12) a (13) obdržíme soustavu čtyř lineárně algebraických rovnic, jejímž řešením jsou integrační konstanty
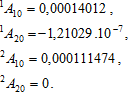
Napjatost v ocelové trubce je opět hlavní. Nejnepříznivější hodnoty jsou na styku oceli a betonu, potom mírně absolutní hodnoty ![]() klesají. Proto uvádíme hodnoty na obou dvou lících trubky. Ještě podotýkáme, že napětí ve směru osy trubky se nemění.
klesají. Proto uvádíme hodnoty na obou dvou lících trubky. Ještě podotýkáme, že napětí ve směru osy trubky se nemění.
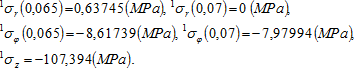
Napjatost v betonu trubku vyplňujícím je konstantní a hlavní, přičemž ![]() nabývají stejných kladných hodnot. Číselně pro náš příklad hodnoty hlavní napjatosti v betonu jsou
nabývají stejných kladných hodnot. Číselně pro náš příklad hodnoty hlavní napjatosti v betonu jsou
Ocelové sloupy vylité betonem jsou celkem standardním konstrukčním prvkem, přesto se naskýtá otázka, zda spřažení betonu a oceli je věnována patřičná pozornost. Z výsledků hlavní napjatosti v betonu je vidět, že použití drátkobetonu je vcelku opodstatněné.
4. Několik poznámek k myšlence spřažených konstrukcí

Obr. 1: da Vinciho nosník
V historických dobách byly návrhy konstrukcí určitým způsobem limitovány přírodními zdroji. To se týkalo nejen kamenných konstrukcí, můžeme vzpomenout řeckou Akropolis, ale i konstrukcí v nichž se větší měrou použily dřevěné prvky. Rozpon při zastropování dřevěnými trámy byl limitován mohutností a výškou stromů rostoucích v lese. Slyšeli jsme, že např. v Británii si netroufali na větší rozpětí, neboť díky klimatickým podmínkám neměli dostatečně mohutné stromy. Na obrázku 1 prezentujeme, že zvýšením únosnosti trámů se zabýval i technický klasik Leonardo da Vinci. Vidíme že v době přednewtonovské a předhookeovské, v době, kdy ještě nevěděli, co je Bernoulliova Navierova hypotéza, si uvědomil, že dva trámy musí spřáhnout, aby se navýšila únosnost a snížil průhyb. Pouhým položením dvou trámů na sebe bychom únosnost prakticky zdvojnásobili, neboť smyku na ploše kontaktu trámů se nedá důvěřovat. Toho si v 15. století všiml i Leonardo da Vinci a navrhl spřažení. Je vidět, že si i uvědomoval, že vrchní vlákna jsou tlačená a spodní tažená. Troufáme si tvrdit, že i přes určitý prořez byla únosnost alespoň trojnásobná, neboť u trámů únosnost roste s kvadrátem výšky.
Vraťme se však k naší úloze zvýšení únosnosti ocelového sloupu tvořeného ocelovou trubkou. Pokud bychom předpokládali, že styku betonu a oceli nemůžeme důvěřovat, jednalo by se o dva nezávislé sloupy, vzhledem ke stejné defomaci, paralelně spojené. Tedy něco podobného, jako když dva trámy položíme na sebe, či vedle sebe. Je celkem paradoxní, že spřažením oceli a betonu namáhání trubky zhoršíme, tlakové napětí při stejné osové deformaci vzroste, v našem případě v absolutní hodnotě o cca 2,5 %. Rovněž i beton si výrazným tahem znatelně pohorší. Takže pokud bychom věděli, že pro náš sloup, asi krátký, je rozhodující porušení tlakem, bylo by dobré jakémukoliv spojení oceli i betonu zabránit. Význam spřažení nachází opodstatnění až v případě, že musíme uvažovat vzpěr. Štíhlost spřaženého sloupu bude určitě menší, ale to už je jiná úloha.
5. Závěr
Co říci závěrem. Někomu by se mohlo zdát, že jsme šli na zajíce s kanónem. Přesto si však myslíme, že některým prezentovaným skutečnostem by měla stavební praxe věnovat pozornost. Pokud zanecháme původní konstrukci a neměníme zatížení, určitě vylitím sloupů betonem únosnost zvýšíme. V případě změn a v případě zvýšení zatížení sloupů stojí prezentované skutečnosti určitě za pozornost.
Poděkování
Příspěvek vznikl v rámci řešení SGS15/031/OHK1/1T/11 Pokročilé numerické modelování v mechanice konstrukcí a materiálů.
Literatura
- [1] Kuklík, P., Transversálně isotropní model v geomechanice, habilitační práce, Fakulta stavební ČVUT v Praze 1991 s. 2–23,
- [2] Kuklik, P., Zalesky, M., Zalesky, J., Theory and comments on standard dilatometric back analysis, Proceedings of the International Conference on Computational & Experimental Engineering and Sciences, Honolulu, Hawaii, USA, 2008, pp. 731–736.
Článek je zaměřen na problematiku vylévání sloupků betonem. Na tento zdánlivě jednoduchý problém autoři pohlížejí poněkud netradičně, poukazují na nezanedbatelné tahové napětí kolmo na osu betonové výplně a zdůrazňují důležitost spolupůsobení. Článek je psán srozumitelně, ilustrace a někdy i poměrně populární forma výkladu rozhodně zvyšují čtivost. Jedná se o zajímavý příspěvek z oblasti praktického problému mechaniky kontinua, který zcela jistě patří na recenzovaný portál TZB-info.
The present contribution deals with the filling of steel columns of the ring cross section by concrete. The question is, how the diversity of the Poisson ratios affect the behavior of the column. Although it seems to be trivial task at the first view, the presented facts could be surprising. Significant transverse tension inside the concrete filling would to be taken into an account.
