Tepelné efekty bodových kotev zavěšených fasádních obkladů
Tloušťky tepelných izolací ve stěnových konstrukcích se již poměrně běžně přibližují k hranici 200 mm a nezřídka ji i výrazně překračují – a to i u objektů, které nemají žádné ambice na zařazení do kategorie nízkoenergetických budov. V souvislosti s tím stoupá potřeba korektního zohlednění vlivu různých tepelných mostů umístěných v takto mohutných tepelně izolačních vrstvách. Mezi typické tepelné mosty, jejichž důsledky již nelze kvůli vzrůstající tloušťce tepelných izolací dále zanedbávat, patří bodové kotevní prvky pro zavěšené fasádní obklady.
Úvodem
Pro upevnění nosné konstrukce vnějšího pláště se u dvouplášťových stěn často používají lehké bodové kotvy z hliníkových či ocelových slitin, jakými jsou např. kotvy SPIDI max (obr. 1).
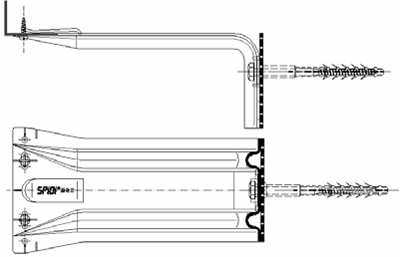
Obr. 1 Kotva SPIDI max 210/80
Tepelný vliv těchto kotev se v projekční praxi dosud spíše zanedbává či se zohledňuje jen orientačními přirážkami k tepelné vodivosti tepelné izolace, v níž jsou kotvy umístěny. Často se doporučuje např. zvýšit tepelnou vodivost o 5 až 15 % v závislosti na předpokládané hmotnosti zavěšeného obkladu. Naneštěstí ale nemusí podobné přirážky vždy dostatečně přesně zohlednit skutečné tepelné působení tohoto typu kotvení. Výsledný efekt kotev nelze totiž vyjádřit nějakou konstantní hodnotou, protože závisí výrazně na celé řadě faktorů počínaje počtem kotev v 1 m2 a konče typem podkladní nosné konstrukce. Přesné zhodnocení tepelného efektu bodové kotvy lze provést jen s pomocí numerického řešení třírozměrného šíření tepla ve 3D charakteristickém výseku konstrukce kolem kotvy.
Numerická analýza
Pro vyjádření tepelných efektů bodových tepelných mostů se používá bodový činitel prostupu tepla χ [W/K]. Vypočte se podle EN ISO 10211-1 z tepelné propustnosti stanovené numerickým výpočtem třírozměrného teplotního pole.
Hodnota bodového činitele prostupu tepla diskutované kotvy je závislá na materiálu kotvy, tloušťce tepelné izolace, izolační podložce pod kotvou a na materiálu nosné stěny. Pro určení míry těchto závislostí byl vytvořen 3D model kotvy s proměnnými tloušťkami izolační podložky pod kotvou a s proměnnou tloušťkou tepelné izolace. Kotva byla modelována přesně včetně prolamování (obr. 2). Těsně kolem kotvy (v jejím prolamování) nebyla uvažována tepelná izolace, ale realističtější uzavřená vzduchová dutina.
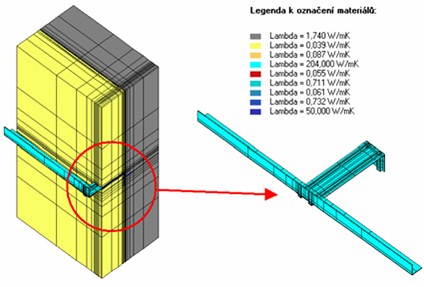
Obr. 2 Model charakteristického výseku s kotvou a částí nosného roštu
Tepelné vodivosti jednotlivých materiálů byly uvažovány podle ČSN 730540-3. Snížené proudění vnějšího vzduchu ve větrané vzduchové vrstvě pod obkladem bylo zohledněno tepelným odporem při přestupu tepla 0,13 m2.K/W, tedy stejným jako na vnitřní straně.
Výsledky výpočtu bodového činitele prostupu tepla v závislosti na tepelném odporu izolační podložky pod kotvou jsou přehledně uvedeny na obr. 3, a to pro různé tepelné odpory nosné stěny. Graf platí pro hliníkovou i ocelovou kotvu a pro tloušťku tepelné izolace 140 mm - obdobné závislosti lze ovšem získat i pro tepelné izolace o jiných tloušťkách (v analýze byly hodnoceny tloušťky od 80 do 260 mm). Ve všech případech byla uvažována styčná plocha kotvy se stěnou o rozměru 90 x 80 mm a kotva o tloušťce stěny 2 mm. Z výsledků je patrná zvláště výrazná závislost bodového činitele prostupu tepla na tepelném odporu stěny. Izolační podložka pod kotvou se projevuje významněji především u stěn s nízkým tepelným odporem (např. u časté železobetonové stěny tl. 200 mm), u nichž je obzvláště výrazná i deformace teplotního pole (obr. 4).
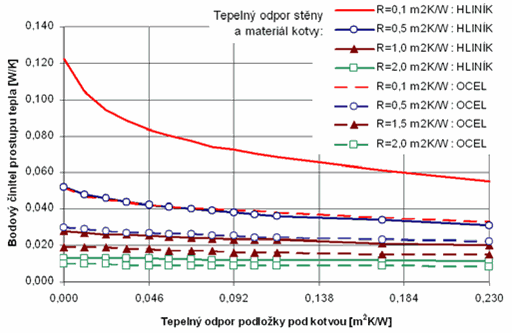
Obr. 3 Bodový činitel prostupu tepla kotvy pro tloušťku tepelné izolace 140 mm
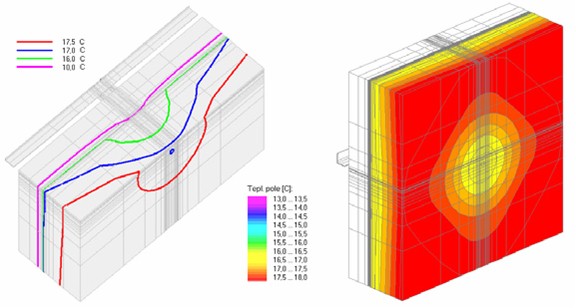
Obr. 4 Izotermy v řezu hliníkovou kotvou a teplotní pole na vnitřním povrchu
(podložka tl. 2 mm, tepelná izolace tl. 140 mm, železobetonová stěna tl. 200 mm)
Vliv kotev na zvýšení součinitele tepelné vodivosti tepelné izolace
Podívejme se nyní na to, jak výrazně mohou kotvy ovlivnit ekvivalentní tepelnou vodivost tepelné izolace, kterou lze stanovit ze vztahu:
![]()
kde d je tloušťka tepelné izolace v m, Rsi a Rse jsou tepelné odpory při přestupu tepla na vnitřní a vnější straně v m2.K/W, Rw je tepelný odpor nosné stěny v m2.K/W a U je součinitel prostupu tepla ve W/(m2.K), který lze stanovit s vlivem kotev jako
![]()
kde R je tepelný odpor konstrukce bez vlivu kotev v m2.K/W, n je počet kotev v 1 m2, χ je bodový činitel prostupu tepla kotvy ve W/K a A je plocha charakteristického výseku v m2 (zde 1 m2).
V Tab. 1 je uvedeno procentuální zvýšení tepelné vodivosti tepelné izolace pro nejnepříznivější stěnu s nízkým tepelným odporem, a to pro dva mezní případy: bez podložky pod kotvou a s podložkou o tl. 16 mm.
| Tep. odpor stěny | Tep. odpor podložky | Kotva | Bod. činitel | Počet kotev v 1 m2 | Ekv. tep. vodivost | Zvýšení tep. vodivosti |
|---|---|---|---|---|---|---|
| Rw [m2.K/W] | Rp [m2.K/W] | χ [W/K] | λeqv [W/(m.K)] | |||
| 0,10 | 0,00 | hliník | 0,12 | 2 | 0,085 | + 113% |
| 3 | 0,112 | + 179 % | ||||
| ocel | 0,05 | 2 | 0,058 | + 44 % | ||
| 3 | 0,067 | + 68 % | ||||
| 0,17 | hliník | 0,06 | 2 | 0,061 | + 54 % | |
| 3 | 0,073 | + 83 % | ||||
| ocel | 0,03 | 2 | 0,050 | + 26 % | ||
| 3 | 0,056 | + 40 % |
Tab. 1 - Vliv kotev na tepelnou vodivost tepelné izolace tl. 140 mm
Z výsledků je zřejmé, že i pro nejpříznivější uvažované kombinace se tepelná vodivost tepelné izolace zvýší o více než 25 %. V nejnepříznivějších situacích (žb stěna, kotvy bez podložek, 3 kotvy/m2) se může tepelná vodivost zvýšit dokonce až na téměř trojnásobek původní hodnoty. Je evidentní, že zanedbávat či podceňovat takto výrazný faktor je hrubou chybou. Pro praktické výpočty je ovšem nereálné provádět vždy podrobnou 3D analýzu vlivu kotev. Pro prvotní analýzy postačí orientační výpočetní postup, který s pomocí jednoduchých vztahů zohlední všechny rozhodující faktory.
Zjednodušená výpočetní metodika
Zjednodušená výpočetní metodika, která bude prezentovaná dále, vychází ze závislostí, které byly zjištěny během rozsáhlé citlivostní analýzy problému. Jedním z východisek pro další odvozování byl charakter závislosti bodového činitele prostupu tepla na tepelném odporu stěny, který je obdobný pro různé tepelné odpory podložky pod kotvou (obr. 5).
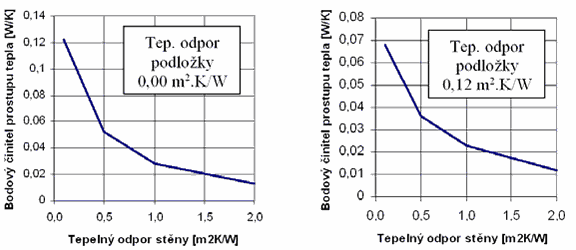
Obr. 5 Závislost bodového činitele prostupu tepla hliníkové kotvy na tepelném odporu stěny
Uvedené křivky lze proložit logaritmickou funkcí ve tvaru:
![]()
v níž koeficienty A a B závisí na tepelném odporu podložky pod kotvou. Tuto závislost lze aproximovat polynomickou funkcí 4. až 6. stupně, takže lze získat vztahy:
a) pro hliníkovou kotvu:
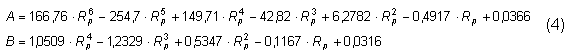
b) pro ocelovou kotvu:
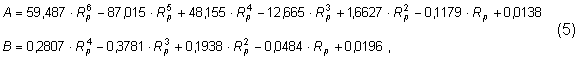
kde Rp je tepelný odpor podložky v m2.K/W.
Výše uvedené rovnice byly odvozeny pro tloušťku tepelné izolace 140 mm, a proto je třeba ve výsledném vztahu pro bodový činitel prostupu tepla ještě zohlednit vliv odlišné tloušťky tepelně izolační vrstvy. Pro hliníkové kotvy lze použít vztah:
![]()
přičemž koeficienty A a B se uvažují podle vztahu (4), Rw je tepelný odpor stěny v m2.K/W, ΔB je korekce pro tenčí podložky (ΔB=0,003 W/K pro Rp do 0,01 m2.K/W; ΔB=0,002 W/K pro Rp od 0,01 do 0,02 m2.K/W; ΔB=0,001 W/K pro Rp od 0,02 do 0,03 m2.K/W; ΔB=0 W/K pro Rp nad 0,03 m2.K/W), Δχ1 je korekce na tloušťku tepelné izolace (Δχ1=0,005 W/K pro tl. izolace nad 140 mm, je-li tepelný odpor stěny vyšší než 0,5 m2.K/W a pro tl. izolace pod 140 mm, je-li tepelný odpor stěny nižší než 0,5 m2.K/W; jinak Δχ1=0 W/K) a Δχ2 je bezpečnostní přirážka (doporučeno 0,002 až 0,005 W/K).
Pro ocelové kotvy lze použít vztah:
![]()
v němž se koeficienty A a B uvažují podle vztahu (5), Δχ1 je korekce na tloušťku tepelné izolace (Δχ1=0,005 W/K pro tl. izolace nad 140 mm, je-li tepelný odpor stěny vyšší než 0,7 m2.K/W a pro tl. izolace pod 140 mm, je-li tepelný odpor stěny nižší než 0,7 m2.K/W; jinak Δχ1=0 W/K) a Δχ2 je bezpečnostní přirážka (viz výše).
Podívejme se ještě závěrem na srovnání výsledků přibližného a přesného 3D výpočtu, a to pro kombinace, které nebyly pro vytvoření zjednodušené metodiky použity. Na obr. 6 je vidět srovnání obou postupů pro dvě různé stěny a tloušťky tepelné izolace. Z výsledků je patrné, že zjednodušená metodika poskytuje pro uvažované případy výsledky s dostatečnou bezpečnostní rezervou, a to i bez zahrnutí bezpečnostní přirážky Δχ2.
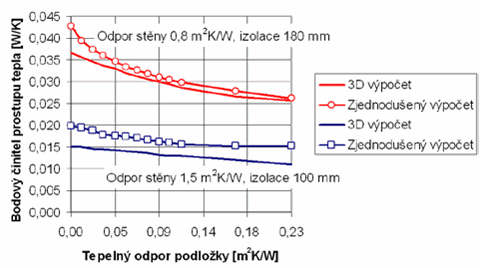
Obr. 6 Porovnání výsledků přesného a zjednodušeného výpočtu pro hliníkovou kotvu
Nově vytvořenou zjednodušenou metodiku výpočtu tepelných efektů bodových kovových kotev lze použít jak při ručním výpočtu, tak především při tvorbě různých programů.
Zbývá uvést omezení zjednodušené metodiky. Použít ji lze pro tepelný odpor nosné stěny od 0,1 do 2,0 m2.K/W, pro tepelný odpor podložky pod kotvou od 0 do 0,4 m2.K/W a pro tloušťku tepelné izolace od 80 do 260 mm. Kotva přitom může být buď hliníková nebo ocelová - tloušťku může mít maximálně 2 mm a styčná plocha kotvy a stěny nesmí překročit 90 x 80 mm.
Tento příspěvek byl podpořen výzkumným záměrem MSM 6840770005.
Literatura:
[1] ŠÁLA, J.: Zateplování budov v praxi. Praha: Grada, 2004.
[2] SVOBODA, Z.: Program Cube3D 2008. Kladno: Svoboda Software, 2007.
[3] Slavonia Baubedarf GesmbH: Dokumentace pro kotvy SPIDI max, 2007.