Nelineárna numerická analýza membránovej konštrukcie
Cieľom nasledujúceho článku je prevedenie modálnej analýzy technickej textílie v tvare hyperbolického paraboloidu. Ide o geometricky nelineárnu membránovú konštrukciu, ktorá je schopná prenášať zaťaženia iba v ťahu. V tomto prípade bolo simulované vlastné kmitanie ako súčasť celkovej dynamickej analýzy. Výsledkom sú vlastné frekvencie a vlastné tvary s pretvoreniami. Získané výsledky prezentujú dynamické správanie sa nelineárnej konštrukcie bez pôsobenia vonkajšieho zaťaženia. Táto analýza tak predstavuje prvý krok a práve vynútené kmitanie ako nelineárna časová analýza doplní v budúcnosti celkovú dynamickú analýzu.

Článek byl vydán v rámci odborné konference doktorského studia Juniorstav 2021. Byl okomentován spolupracovníky redakce TZB Info.
1. Úvod
Membrány môžeme definovať ako materiál 6. generácie po tradičných materiáloch ako tehla, drevo, kameň, oceľ a betón. Membránové konštrukcie sú vytvárané z technických textílií. Ide o materiál, ktorý má veľmi malú hmotnosť a používajú sa hlavne na preklenutie veľkých rozpätí bez potreby medziľahlých podpier. Z týchto faktov vyplýva úspora materiálu, a teda zníženie počiatočných nákladov. Tento ekonomický aspekt podtrhuje fakt, že membrány fungujú iba v ťahu, čím využívajú svoje pozitívne vlastnosti, ktoré sa odrážajú v predĺžení ich vlastnej životnosti.
Ale rovnako ako akýkoľvek iný materiál, aj technické textílie majú svoje negatíva. Ide o silne geometricky nelineárne konštrukcie, ktoré majú náročnejšiu fázu návrhu. Na rozdiel od tradičných materiálov menia membrány svoj tvar v závislosti od pôsobiaceho zaťaženia, takže musíme pristupovať k výpočtom krok po kroku. Nelineárna analýza s iteračným procesom je tak neodmysliteľnou súčasťou numerickej simulácie a analýzy.
Ďalším špecifikom membrán je nutnosť ich predopnutia na zabezpečenie prenosu zaťaženia. Keďže sú technické textílie vo svojej podstate iba tkaniny, počiatočné podmienky si vyžadujú definovanie predpätia membránového povrchu. Keďže ich potrebujeme predopnúť, nepoznáme ich začiatočný tvar. Na tento účel slúži proces form-findingu, ktorý hľadá rovnováhu medzi predpätím a deformáciou, resp. začiatočným tvarom.
Form-finding je špecifický krok pri návrhu membránových konštrukcií, bez ktorého nie je možné pokračovať statickou alebo dynamickou analýzou. Na tento účel nestačia jednoduché matematické postupy. Kedysi sa používali rôzne fyzické modely, dnes sú to vhodné výpočtové metódy.
Vo všeobecnosti pozostávajú membránové konštrukcie z 3 základných častí: technická textília ako plošný prvok, stabilizujúci líniový prvok zabezpečujúci predpätie (lano, tuhý prvok) a základná nosná konštrukcia, ktorá umožňuje prenos vnútorných síl do podložia.
2. Použitie membrán
![Obr. 1 Nemecký pavilón na Svetovom Expo [1]](/docu/clanky/0229/022913o2.jpg)
Obr. 1 Nemecký pavilón na Svetovom Expo [1]
Konštrukcie ľahkej architektúry, ktoré zahŕňajú aj skúmané membrány, môžeme definovať schopnosťou prenášať rovnaké množstvo zaťaženia pri nižšej vlastnej hmotnosti vzhľadom na vnútorné sily. A rovnako ako akékoľvek iné konštrukcie, aj textilné konštrukcie podliehajú prísnym požiadavkám na mechanickú odolnosť a stabilitu vzhľadom na špecifiká uvedené v predošlej kapitole.
Použitie membránových konštrukcií sa datuje tisíce rokov dozadu, a to formou dočasných zastrešení a stanov, napríklad cirkusový stan chapitteau. Konštrukcie ľahkej architektúry vo forme, v akej ich poznáme dnes, začali dizertačnou prácou Otta Freia „Das Hägende Dach“ v roku 1952. V roku 1967 sa Otto Frei zúčastnil návrhu Nemeckého pavilónu (Obr. 1) na Svetovom Expe v Montreale. Hoci bol pôvodný návrh pavilónu tvorený nosnou konštrukciou membrány, nakoniec bol skonštruovaný ako lanová sieť s dodatočným prekrytím technickou textíliou [1].
3. Numerický model
Na uskutočnenie numerickej analýzy bola namodelovaná membrána v tvare hyperbolického paraboloidu. Bol použitý MKP softvér Dlubal RFEM. Táto 3D konštrukcia je tvorená ortotropným materiálom, ktorý má rôzne vlastnosti v dvoch na seba kolmých smeroch. V hlavnom smere (nazývaný smer osnovy) má membrána modul pružnosti Ex = 1 057 MPa, v smere útku je modul Ey = 612 MPa [2]. Tieto hodnoty prezentujú charakteristiky dané od výrobcu technickej textílie Serge Ferrari Précontraint 502.
Ďalší parameter, ktorý charakterizuje numerický model, je pôdorysný rozmer 2 × 2 m s celkovou výškou 1 m. Na okrajoch plošného prvku sú namodelované lineárne prvky – laná s priemerom 8 mm. Ide o prvky s nerezovej ocele s modulom pružnosti E = 130 GPa. Zabezpečujú v konštrukcii predpätie prostredníctvom definovaného previsu s veľkosťou 0,2 m. Predpätie membrány je v oboch smeroch (v smere osnovy a útku) rovnaké a má hodnotu nx = ny = 4 kN/m2.
Membrána stabilizovaná okrajovými lanami je kotvená pomocou 2 kotevných tyčí a 2 akčných prvkov. Akčné prvky, alebo aktuátory, sú elementy, ktoré môžu meniť svoju dĺžku a tak meniť samotné predpätie membrány. Zapojením týchto prvok sa z membrány stáva aktívna konštrukcia. Táto možnosť zmeny dĺžky a predpätia v tomto prípade nebola uvažovaná.
Kotvenie je modelované formou plných kruhových prierezov D46 a D145. Tieto prierezy prezentujú hmotu na reálnom experimentálnom zariadení, na ktorom budú verifikované numerické modely v ďalších krokoch výskumu.
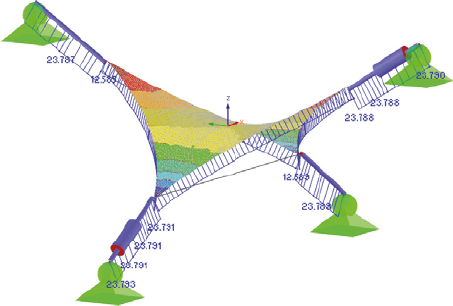
Obr. 2 Membrána po form-findingu
Keďže Dlubal RFEM počíta metódou konečných prvkov, v tomto prípade bolo zvolené nasledujúce delenie siete: 1D prvky ako kotvenie a okrajové laná sa delia na 10 dielikov na prvok, 2D plošné elementy membrán vo forme trojuholníkových konečných prvkov majú dĺžku hrany nastavenú na 50 mm [3], [4]. Membrána, ako priestorový prvok, bola modelovaná ako 2 trojuholníky so spoločnou spodnou hranou a hornými vrcholmi.
Pred tým ako dôjde k spusteniu akéhokoľvek statického alebo dynamického výpočtu, musí namodelovaná konštrukcia prejsť procesom form-findingu, ktorého cieľom je nájsť začiatočný stav v závislosti od predpätia. Dlubal RFEM používa pre túto potrebu Update Reference Strategy (URS). V podstate sa konštrukcia zaťažuje predpätím krok za krokom a trasuje sa pretvorenie uzlov konečných prvkov [5].
Na Obr. 2 sú vyobrazené napätia na membráne a vnútorné sily v kotvení po spustení form-findingu. Je dôležité poznamenať, že form-finding počíta bez uváženia vlastnej tiaže.
4. Modálna analýza a výsledky
Dlubal RFEM, ako MKP softvér, má k dispozícii niekoľko add-on modulov. Jedným z nich je aj RF-DYNAM PRO, ktorý slúži na dynamickú analýzu. V tomto článku bola uskutočnená analýza vlastného kmitania, výsledkom ktorej sú vlastné frekvencie a vlastné tvary. Vytvorený bol 1 hmotový stav, definovaný ako stály, prezentujúci vlastnú tiaž konštrukcie.
Z tohoto hmotového stavu bol následne vytvorený 1 stav vlastného kmitania. Minimálny počet vlastných tvarov bol stanovený na 10, úprava vlastných tvarov bola zvolená na základe odporúčania podľa manuálu (pre nelineárnu analýzu) na {uj}T [M] {uj} = 1 [6].
Pre počítaný stav vlastného kmitania bola uvažovaná konzistentná matica tuhosti a Lanczosova metóda pre výpočet vlastných čísel. Je dôležité podotknúť, že v tomto stave bola upravená tuhosť konštrukcie prebratím tuhosti zo stavu form-finding.
V Tab. 1 je možné vidieť všetkých 10 vlastných tvarov s uvážením vlastnej tiaže, ich uhlové frekvencie ω a periódy T. Na Obr. 3 je možné vidieť tieto vlastné tvary spolu s maximálnou výchylkou.
| Vlastný tvar | Uhlová frekvencia ω [rad/s] | Vlastná frekvencia f [Hz] | Vlastná perióda T [s] |
|---|---|---|---|
| 1 | 57,194 | 9,103 | 0,110 |
| 2 | 60,423 | 9,617 | 0,104 |
| 3 | 66,525 | 10,588 | 0,094 |
| 4 | 92,430 | 14,711 | 0,068 |
| 5 | 99,507 | 15,837 | 0,063 |
| 6 | 180,117 | 28,667 | 0,035 |
| 7 | 220,290 | 35,060 | 0,029 |
| 8 | 314,971 | 50,129 | 0,020 |
| 9 | 344,839 | 54,883 | 0,018 |
| 10 | 378,327 | 60,213 | 0,017 |
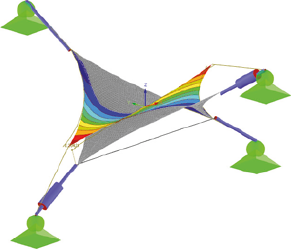
1. vlastný tvar
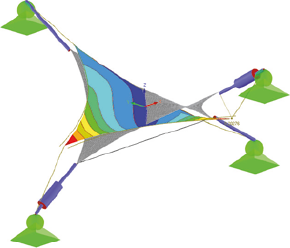
2. vlastný tvar
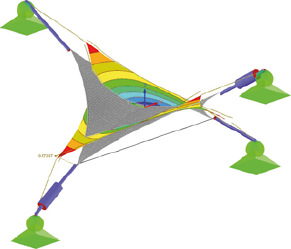
3. vlastný tvar
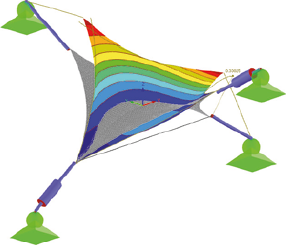
4. vlastný tvar
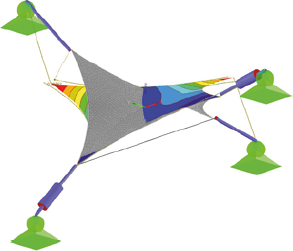
5. vlastný tvar
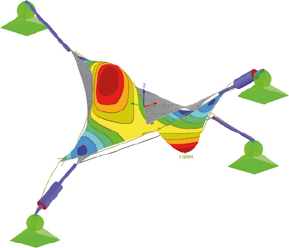
6. vlastný tvar
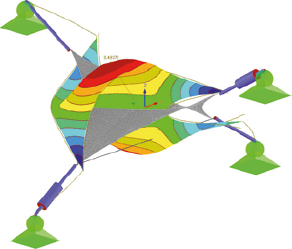
7. vlastný tvar
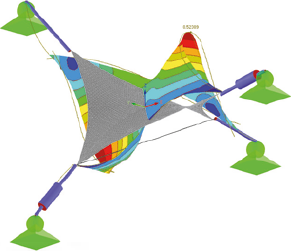
8. vlastný tvar
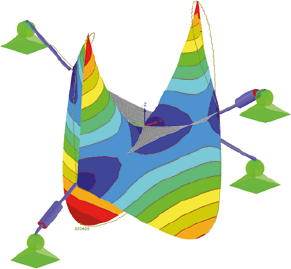
9. vlastný tvar
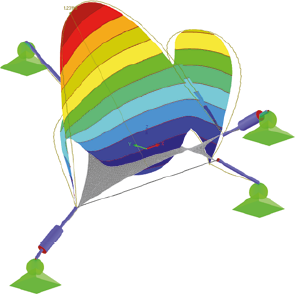
10. vlastný tvar
Obr. 3 Zobrazenie vlastných tvarov
5. Záver
Cieľom tohoto príspevku bolo uskutočniť modálnu analýzu. Vo výsledku sme dostali hodnoty vlastného kmitania membránovej konštrukcie. Táto konštrukcia je silne geometricky nelineárna a vyžaduje si špecifický krok pred samotnou statickou alebo dynamickou analýzou. Tento krok robí membrány výnimočnými v porovnaní s typickými materiálmi.
Ako je možné vidieť v Tab. 1 a na Obr. 3, najnižšia vlastná frekvencia je mierne vyššia než 9 Hz. Môžeme tak povedať, že frekvencia je nižšia ako 10 Hz, čo prezentuje dynamický vietor, avšak je vzdialená hodnote 5 Hz, ktorá je signifikantná pre dynamický vietor. V tomto prípade je nutné domodelovať oceľový rám, v ktorom je konštrukcia membrány uložená rovnako ako je to na reálnom experimentálnom zariadení v laboratóriu. Tento krok bude mať významný vplyv na výsledky vlastného kmitania a dynamickej analýzy.
Taktiež je nutné v budúcnosti uskutočniť analýzu s vynúteným kmitaním, čo rozšíri tento výskum. Či už to bude harmonické, periodické kmitanie s uvážením a bez uváženia tlmenia.
Všetky tieto kroky je nutné na záver porovnať s výsledkami získanými z experimentálneho zariadenia.
Poďakovanie
Vypracovanie tohto výskumu a článku je podporované Agentúrou na podporu výskumu a vývoja, č. zmluvy APVV-15-0777 a Vedeckou grantovou agentúrou, č. mluvy VEGA 1/0129/20.
Použité zdroje
- FOSTER, Brian a Marijke MOLLAERT. European Design Guide FOr Tensile Surface Structures. Germany: Tensinet, 2003.
- INOVA, Praha s.r.o. Dokumentácia k skúšobnému zariadeniu – 17 120: časť 1 – Plachtostroj. Praha: INOVA Praha, 2017.
- KAPOLKA, Lukáš. Analysis of an experimental tension structure. In: IOP Conference Series: Materials Science and Engineering. Bristol, 2019, s. 6.
- ŠOLTÝS, Róbert a Michal TOMKO. Analýza kmitania lana zaťaženého vetrom. In: Juniorstav 2012: 14. odborná konference doktorského studia. Brno: Vysoké Učení Technické V Brně, 2012.
- DLUBAL, RFEM 5. Spatial Models Calculated According to Finite Element Method User Manual. Germany: Dlubal Software, 2019.
- DLUBAL, RF-DYNAM Pro. Natural Vibration Analysis, Response Spectra, Time History, Equivalent Static Forces Program Description. Germany: Dlubal Software, 2019.
Článek prezentuje numerické řešení vlastního kmitání textilní membrány z materiálu Précontraint FERRARI® 502S formované do tvaru HP. Poskytuje tak základní představu o vlastních tvarech a postupu dalšího řešení dynamického chování membrán. Článek naznačuje další kroky bádání tohoto renomovaného pracoviště v oblasti TFS (tensile fabric structures) pod vedením prof. Kmetě, zohlednění vlivů předpětí membrány i okrajových prvků, ortotropního chování membrán i experimentálního vyšetřování. Článek zapadá do konceptu JUNIORSTAV. Studentům náleží pochvala za řešení obtížného nelineárního problému.
The aim of this paper is the modal analysis of a thin technical textile in shape of hyperbolic paraboloid. It is the geometrically nonlinear membrane structure, which can function only in tension. In this case, the structure was subjected to the natural vibration as a part of the overall dynamic analysis. All of this results in natural frequencies and mode shapes and deflections. Acquired results describe the dynamic behaviour of nonlinear system without affect of the external load. This part could represent a first step in the dynamic analysis and exactly the forced vibration as nonlinear time history analysis will have to be performed in a future to complete it.