Numerické řešení vlivu vegetační vrstvy na teplotu v jednotlivých vrstvách vegetační ploché střechy
Předložená práce se zabývá posouzením vlivu typu a materiálové skladby střechy na průběh teplot ve střešní konstrukci. K analýze využívá dynamickou metodu a ve výsledku dokumentuje příznivý účinek vegetační střechy a z tepelnětechnického hlediska pozitivní důsledek na teplotní poměry ve stavbě.
1. Úvod
Pojem vegetační střecha je chápán jako střecha, která je částečně nebo zcela pokrytá vegetací, která je umístěna nad hydroizolační vrstvou. Skladba vegetační střechy, na rozdíl od střechy s klasickým pořadím vrstev, obsahuje vegetační souvrství, které se zpravidla skládá z vrstev následujících: vegetační, separační, hydroakumulační, filtrační, drenážní, separační a dilatační vrstva a případně také vrstva ochranná (v případě, že pro hydroizolaci není použito asfaltových pásů, které vykazují odolnost proti prorůstání kořeny rostlin). Vegetační střechy jsou známy již z období Babylonu cca 1000 let před naším letopočtem. Navzdory této skutečnosti lidé o zmíněné střešní konstrukci stále pochybují. V dnešní době se navíc nenavrhují pouze jednoduché formy zeleně, ale i složité střešní zahrady.
Vegetační střechy se provádějí nejen kvůli jejich estetickému a ekologickému hledisku, ale mají také podíl na úspoře energie budovy, díky lepším tepelně technickým vlastnostem střešní konstrukce. Vývoj počítačového modelování má svou vlastní bohatou historii [1], aplikace různých software na vegetační střechy je uváděna v [2] a [3]. Nicméně všechny tyto software pracují se zjednodušením a zanedbávají i některé fyzikální procesy, jak uvádí [4]. V tomto příspěvku je představen vliv zeminy na průběh teplot ve střešní konstrukci zjištěný řešením nestacionárního tepelného šíření a s využitím klimatických údajů platných pro Brno Tuřany v roli okrajových podmínek.
2. Vztahy pro výpočet vazebného tepelného toku
Vazebným prvkem mezi jednotlivými místnostmi je tepelný tok, tedy vazebný tepelný tok [6]. Při šíření tepla mezi místnostmi v budově jej lze rozlišit na tyto složky:
- přestup tepla mezi okolním vzduchem a povrchem stěny:
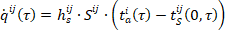 (1)
(1)
- šíření tepla stěnou. Jde o Fourierovu rovnici vedení tepla pro jednorozměrný případ:
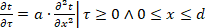 (2)
(2)
Počáteční a okrajové podmínky:
- počáteční teplota
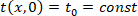 (3)
(3)
- okrajové
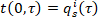 , resp.
, resp. 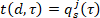 (4)
(4)
- počáteční teplota
- šíření mezi okolním vzduchem a povrchem stěny
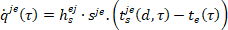 (5)
(5)
- toky ventilačního vzduchu a spárové netěsnosti v místnosti
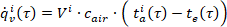 (6)
(6)
- tepelná radiace mezi vnitřními povrchy v místnosti
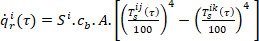 (7)
(7)
Spočtením rovnice b) stanovíme povrchové teploty konstrukce t(x,τ), pro i-tou místnost t i j(0, τ), resp. t i j(d, τ) na opačném povrchu stěny. Odsud lze určit vazebné tepelné toky mezi jednotlivými místnostmi qi js (τ). J. Řehánek [5] navrhnul řešení tepelných vazeb v objektu vztahem odvozeným z Fourierovy metody řešení Fourierovy rovnice vedení tepla, který platí v analytické formě však jen pro jednovrstvé stěny. Pro každou místnost systému lze sestavit bilanční rovnici:
přičemž dílčí tepelné toky bilanční rovnice lze formulovat vztahy (9) až (13):
- tepelný tok proudící stěnou
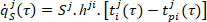 (9)
(9)
- tepelný tok vnějšími prosvětlovacími otvory
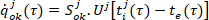 (10)
(10)
- tepelný tok vnitřními otvory (dveřmi)
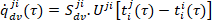 (11)
(11)
- ventilační tepelný tok
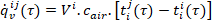 (12)
(12)
- tepelný tok osluněním
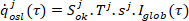 (13)
(13)
Použité symboly:
- t
- teplota
- τ
- čas
- x
- vzdálenost od vnitřního líce stěny 0 ≤ x ≤ d podle její tloušťky d
- A
- pohltivost sálání; součinitel vzájemného sálání povrchů stěn
- cair
- objemová tepelná kapacita vzduchu (za normálních podmínek)
- cb
- součinitel sání černého tělesa (asi 5,67.10−8 W·m−2·K−4)
- hi js
- součinitel přestupu tepla stěny v i-té místnosti mezi i a j místností
- Iglob (τ)
- časově závislá intenzita globálního slunečního záření
- qis (τ)
- časově závislá okrajová podmínka tepelného systému budovy i-té místnosti
- q̇i j(τ)
- časově závislý tepelný tok mezi i a j místností
- q̇iv (τ)
- časově závislý tepelný tok infiltrací vzduchu do i-té místnosti
- Qm (τ)
- časově závislý tepelný obsah m-té místnosti
- Qm,jztráty (τ)
- časově závislá j tepelná ztráta m-té místnosti
- Qm,izisky (τ)
- časově závislý i tepelný zisk m-té místnosti
- Si j
- plocha dělicí stěny mezi i-tou a j-tou místností
- Sjok ; Sjdv
- plocha okna; dveří v j-té místnosti
- Ti js (τ)
- časově závislá termodymická povrchová teplota stěny mezi i a j místností v i-té místnosti
- t0
- počáteční teplota rozložení teplot ve stěně
- tia (τ)
- časově závislá teplota vzduchu v i-té místnosti
- ti js (0,τ)
- časově závislá povrchová teplota stěny mezi i a j místností v i-té místnosti
- te (τ)
- časově závislá teplota vnějšího prostředí
- T j
- činitel prostupu slunečního záření zasklením vnějšího prosvětlovacího otvoru v j-té místnosti
- U j
- součinitel prostupu tepla vnějšího prosvětlovacího otvoru v j-té místnosti
- U ji
- součinitel prostupu tepla vnitřními otvory (dveřmi) mezi j a i-tou místností
- V i
- objem i-té místnosti
3. Nestacionární výpočet průběhu teplot ve stěnách
Průběh teplot lze stanovit s podporou vlastního software. Výsledky výpočtů rozdělení teplot nejsou za být reálných podmínek příliš rozdílné od skutečného stavu, protože okrajové podmínky, které vstupují do výpočtu, byly odvozeny z dlouhodobých klimatických měření. Za pomoci strojového programu byl naprogramován výpočet průběhu teplot s časově proměnnými exteriérovými okrajovými podmínkami, přitom byl také zohledněn výpočet pohybu slunce po obloze s využitím složky globální i difuzního slunečního záření a v té souvislosti změny sálavého solárního toku během dne. Jak bylo zmíněno výše, hodnoty exteriérových teplot a oslunění byly využity z meteorologické stanice z letiště Brno Tuřany podle dat odvozených z řady let meteorologických měření za sebou, které se blíží údajům referenčního klimatického roku.
Modelován byl menší objekt o jednom nadzemním podlaží a pěti místnostech. V prvním výpočtu byla uvažována skladba ploché střechy s klasickým pořadím vrstev a do druhého výpočtu byla započítána i zemina, a to jednou o mocnosti 100 mm a podruhé o mocnosti 300 mm. Podrobnější skladba střešní konstrukce je znázorněna na obrázcích 2 a 3.
3.1 Průběh teplot v klasické ploché střeše
![Graf 1: Výpočtový průběh teplot v klasické ploché střeše podle obrázku 2 [zdroj: vlastní]](/docu/clanky/0220/022048o21.png)
Graf 1: Výpočtový průběh teplot v klasické ploché střeše podle obrázku 2 [zdroj: vlastní]
Maximální vypočtená povrchová teplota na této konstrukci byla 59,4 °C, a to 22. června ve 12 hodin odpoledne. Naopak nejnižší teplota byla vypočtena dne 25. ledna v 8 hodin ráno, a to −9,3 °C. Grafický průběh teplot je znázorněn v grafu 1.
V grafu 1 hodnoty t3,Se až tSi,1 zobrazují teploty na površích a rozhraní materiálů stropní konstrukce. Hodnota t3,Se je teplota na venkovním povrchu konstrukce, hodnota t2,3 je teplota na rozhraní tepelné izolace a nosné stropní konstrukce, t1,2 zase znázorňuje teplotu na rozhrání stropní konstrukce a vnitřní omítky a hodnota tSi,1 je vnitřní povrchová teplota na podhledové omítce.
3.2 Průběh teplot v ploché vegetační střeše se 100 mm zeminy
![Graf 2: Výpočtový průběh teplot v ploché vegetační střeše se 100 mm zeminy [zdroj: vlastní]](/docu/clanky/0220/022048o22.png)
Graf 2: Výpočtový průběh teplot v ploché vegetační střeše se 100 mm zeminy [zdroj: vlastní]
Výpočtem jsme zjistili maximální teplotu pro den 22. června ve 12:00, a to 54,5 °C. Zde je vidět snížení o necelých 5 K oproti ploché střeše bez zeminy. Nejnižší teplota byla zjištěna naměřena −11,1 °C pro den 25. ledna v 8:00. Graf 2 znázorňuje průběh teplot této konstrukce v celém roce.
3.3 Průběh teplot v ploché vegetační střeše s 300 mm zeminy
![Graf 3: Výpočtový průběh teplot v ploché vegetační střeše s 300 mm zeminy [zdroj: vlastní]](/docu/clanky/0220/022048o23.png)
Graf 3: Výpočtový průběh teplot v ploché vegetační střeše s 300 mm zeminy [zdroj: vlastní]
Pro den 22. června byla vypočtena nejvyšší teplota na povrchu střešní konstrukce za celý rok, a to 48,1 °C. Od střechy bez zeminy se tato teplota liší o 11 K a od střechy s mocností zeminy 100 mm o 6 K. Z toho lze soudit, že záleží i na mocnosti vrstvy zeminy použité ve skladbě střešního pláště. Nejnižší naměřená teplota činí −9,7 °C, a to pro den 25. ledna v 8 hodin ráno. Podrobnější průběh je uveden v grafu 3.
U grafu 2 a 3 je hodnota t4,Se teplota na venkovním povrchu konstrukce, hodnota t3,4 je teplota na rozhraní zeminy a tepelné izolace, kde jsme zanedbali vliv hydroizolace, která by ovlivnila výslednou teplotu jen minimálně, t2,3 znázorňuje teplotu rozhraní tepelné izolace a stropní konstrukce, t1,2 znázorňuje teplotu na přechodu stropní konstrukce a vnitřní omítky a hodnota tSi,1 je povrchová teplota vnitřní omítky.
4. Závěr
Cílem tohoto příspěvku bylo prokázat reálnější pohled na účinnost konstrukce vegetační střechy z hlediska snížení letní exteriérové povrchové teploty díky vrstvě zemině umístěné na střeše. V příspěvku je využito výpočtových teplotních průběhů v konstrukci vegetační střechy, bylo využito nestacionárního řešení teplot v konstrukci střechy a obecné metodiky řešení tepelného systému budovy podle popisu J. Řehánka. Snížení teplotního zatížení podstřešních prostor se podařilo výpočtově prokázat díky značné tepelné jímavosti zeminy. Vypočtené hodnoty se ovšem mohou od reality lišit, neboť teplotu na povrchu konstrukce ovlivní i volba vysazené zeleně, závlahové poměry, zhutnění zeminy aj. Obecně listy zeleně pohltí velké množství tepla, to se však ve výpočtu zohlednit nepodařilo. Potom lze ve skutečnosti očekávat, že zjištěné teploty by byly být příznivější oproti provedené výpočtové simulaci.
Uvedený příspěvek má dokumentovat příznivý účinek vegetační střechy – z tepelně technického hlediska pozitivní důsledek na teplotní poměry v podstřešním prostoru i ve stavbě samotné. Takový projev lze zachytit pouze tehdy, jestliže se teplotní průběh posuzuje nestacionárně s využitím denního chodu reálných okrajových klimatických teplot. Použitím stacionárních nebo kvazistacionárních okrajových klimatických teplot, které se obvykle využívají pro stanovení energetické náročnosti budov, se uvedený účinek zachytit nepodaří.
Simulační výpočet, v němž se uplatní zejména materiálové vlastnosti použitých staviv, zejména součinitel tepelné vodivosti, objemová hmotnost i tepelná kapacita, umožňuje vystihnout reálný obraz o teplotních pochodech probíhajících nejen ve střešní konstrukci, nýbrž ve všech plošných konstrukcích celého stavebního objektu a také posouzení právě vlivu použitých staviv pro výstavbu objektu.
Tento článek byl vytvořen s využitím dříve publikovaného odborného článku Majsniar, M.; Šťastník, S., Tepelná stabilita objektu při použití zelené střechy, příspěvek na konferenci Juniorstav 2015, ISBN 978-80-214-5091-2, Vysoké učení technické v Brně, Fakulta stavební, 2015, s úpravami podle doporučení redakce TZB-info a recenzenta.
5. Literatura
- VALA, J., ŠŤASTNÍK, S. On the thermal stability of dwelling structures. Building Research Journal 52 (2004), p. 31–55.
- AYATA, T., TABAREZ-VELASCO, P. C., SREBRIC, J. An investigation of sensible heat fluxes at a green roof in a laboratory setup. Building and Environment 46 (2001), p. 1851–1861.
- CAPOZZOLI, A., GORRINO, A. CORRADO, V. Thermal characterisation of green roofs trough dynamic simulation. Proceedings of BS 2013 (13th Conference of International Building Performance Simulation Association), Chambérech (France), IBPSA, 2013, p. 3630–3637.
- VALA, J. Numerical aspects of the identification of thermal characteristics using the hot-wire method. Proceedings of PANM 2013 (15th Conference on Programs and Algorithms of Numerical Mathematics) v Dolním Maxově (Czech Republic), Mathematical Institute AS CR 2012, p. 187–194.
- ŘEHÁNEK, J., Dynamika tepelného stavu vnitřního prostředí, Tepelná ochrana budov 3/99, 2. ročník, 1999, str. 3–4.
Příspěvek pojednává o problematice matematického modelování vlivu vegetační vrstvy (resp. její tepelněakumulační schopnosti) na teploty jednotlivých vrstev ve skladbě vegetačních plochých střech. Může být velmi přínosný pro všechny, kteří se zabývají problematikou navrhování střech či tepelně-technickou problematikou budov.
The presented paper strives to assess the influence of the type and material composition of the roof on the course of temperatures in the roof structure by the so-called dynamic method.
![Obr. 1: Schéma uspořádání vazebných tepelných toků uvnitř a vně budovy podle popisu J. Řehánka [5]](/docu/clanky/0220/022048o10.png)
![Obr. 2: Schéma ploché střechy s klasickým pořadím vrstev [zdroj: vlastní]](/docu/clanky/0220/022048o18.png)
![Obr. 3: Schéma skladby střechy s vegetační vrstvou [zdroj: vlastní]](/docu/clanky/0220/022048o20.png)