Částečná požární ochrana ocelových konstrukcí – část 1: Shrnutí teoretických poznatků
Tento článek se zaměřuje na částečnou požární ochranu ocelových konstrukcí a poskytuje teoretický přehled současných metod a materiálů používaných v tomto oboru. Jsou představeny různé typy pasivních požárních ochranných systémů, včetně intumescentních nátěrů a jejich vlivu na tepelný přenos mezi chráněnými a nechráněnými částmi konstrukce. Článek se zabývá analytickými a matematickými metodami pro stanovení tepelných vlastností a požární odolnosti použitých materiálů, s důrazem na ty, které podléhají tepelné degradaci. Tento článek poskytuje ucelený pohled na teoretické základy částečné požární ochrany ocelových konstrukcí a nabízí směry pro další výzkum v této oblasti a poskytuje základ pro Část 2: Experimenty, numerické modely a srovnání.
1. Úvod
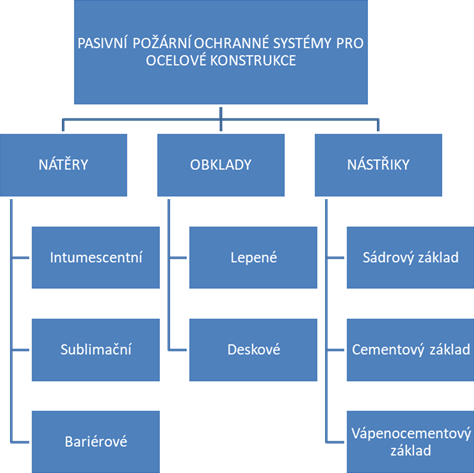
Pasivní požární ochrana je základem požární bezpečnosti ocelových konstrukcí, které jsou subtilní a vedou dobře teplo. Využívá se řady metod a typů ochrany; viz obr. 1. Obvykle se se chrání jednotlivé prvky konstrukce ochrannými nátěry, nástřiky nebo obklady. Dříve se tepelně izolovalo na danou teplotu. Nyní na požadovanou požární odolnost daného prvku. Často stačí pouze hlavní prvky konstrukce, a posoudit celkové působení celé konstrukce, nejčastěji ocelobetonového stropu, plošiny nebo jiné nosné konstrukce. Lze využít membránové působení ocelobetonové desky s nechráněnými prvky. Chrání se pouze sloupy a průvlaky a styčníky konstrukce. Poznatky jsou schnuty v hlavních studiích o částečné požární ochraně ocelových konstrukcí [1] a [2]. K dispozici jsou i další materiály [3], [4], [5] a [6]. Většina studií se zabývá intumescentními nátěry a jejich vlivem na přestup tepla z nechráněné konstrukce do chráněné konstrukce. Teplo je vedeno z teplejších prvků do chladnějších [7], [8], [9] a [10]. Jedná se o dobře popsaný jev a matematické nebo analytické metody pro jeho stanovení jsou připraveny. Velký vliv na výsledky mají zvolené vstupní údaje, okrajové podmínky a tepelné vlastnosti materiálu. U materiálů, které podléhají tepelné degradaci nebo obsahují vodu nebo obojí současně, je třeba zahrnout změnu tepelné vodivosti při zvýšené teplotě za požáru. Změna měrné a objemové hmotnosti se neuvažuje. Přenos tepla probíhá vedením v pevném materiálu [11]. Dále je třeba zohlednit způsob zahřívání ocelových prvků, vliv emisivity a součinitele přestupu tepla do konstrukce. Požadovaná požární odolnost závisí hlavně na poměru mezi exponovanou plochou prvku, na kterou působí teplota při požáru, a objemem průřezu. Tento poměr, součinitel průřezu, je uveden v rozměrových tabulkách pro určení použitelnosti ochranných materiálů pro konkrétní prvek [12], [13] a [14]. Komplexní srovnání a výstupy z experimentů, numerických modelů a parametrické studie shrnul Šejna a kol. [15], tento článek shrnuje poznatky a možnosti při návrhu.
Podle materiálu a způsobu použití lze požární obklady rozdělit na deskové, nátěry a nástřiky. Deskové obklady se umísťují přímo na chráněný prvek nebo na pomocnou konstrukci, jako je například ocelový rošt. Funkce opláštění je omezena nejmenšími detaily, například kvůli špatné pomocné konstrukci nebo spojům mezi deskami [16], [17]. Z těchto důvodů je při aplikaci požární ochrany nezbytné přesně dodržovat pokyny výrobce systému. Základním parametrem při výběru materiálu desek pro požární opláštění je relativní vlhkost v požárním úseku, kde má být opláštění aplikováno. Vysoké hodnoty vlhkosti mohou způsobit, že deska při požáru popraská. Mezi obklady, které jsou náchylné k prasknutí při dlouhodobém vystavení vysokým hodnotám vlhkosti, lze uvést desky na bázi vermikulitu, které v takovém prostředí degradují a ztrácejí pevnost. Při aplikaci pasivní požární ochrany je výhodnější rozložit požadovanou tloušťku obkladu do více vrstev desek vrstvených na sebe než aplikovat pouze jednu desku dané tloušťky. V prostoru pod obkladem vzniká agresivní prostředí, které může vést ke korozi chráněných prvků, a tím může snížit jejich životnost. Je důležité chráněný prvek před instalací ochranných desek důkladně ošetřit antikorozním nátěrem. Se stejným problémem se lze setkat v korozivním prostředí a na průmyslových stavbách, kde může docházet ke korozi široce používaných spojovacích prvků. V důsledku toho může dojít k otevření spojů mezi deskami nebo k rozpadu celého systému již po několika letech v takovém prostředí. Je nutné zvolit vhodný materiál nejen pro desku, ale také pro spojovací materiál, v závislosti na typu prostředí. V případě lepeného opláštění se na chráněný prvek lepí deska z čedičové plsti se sníženým obsahem lepidla [18], [19], [20].
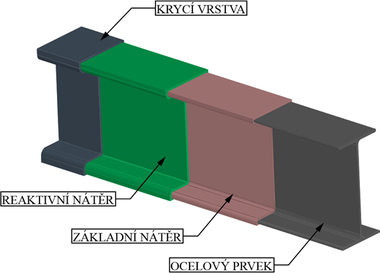
Intumescentní nátěry [21], [22], [23], [24], [25] jsou ucelený systém, který sestává ze základního nátěru, funkční vrstvy a vrchního nátěru. Vrstvy intumescentních nátěrů na sebe za přesně stanovených podmínek vzájemně působí, Vrstvy aplikují se v požadované kvalitě a tloušťce, viz obr. 2. Základní nátěr má vykazovat dostatečnou přilnavost k povrchu, který má být chráněn, a musí vykazovat stabilitu až do okamžiku napěnění funkční vrstvy. Současně mít dostatečnou ochranu proti korozi, aby chránil ocelový prvek. Vrchní nátěr nemusí plnit pouze estetickou funkci. Jeho dalšími funkcemi mohou být například ochrana proti okolní vlhkosti, UV záření a případnému drobnému mechanickému poškození [26] a [27]. Kromě toho se musí před vypěněním vypálit [28], [29], [30] a [31].
2. Částečně požárně chráněné ocelové konstrukce
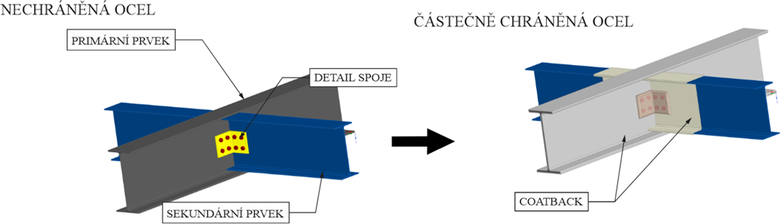
U stropních konstrukcí s nechráněnými stropnicemi se teplo přenáší vedením do spojů a průvlaků díky dobré tepelné vodivosti oceli. Částečné požární ochrany se využívá například pro stropnice v oblasti spoje. Omezí se přenos tepla. V britské angličtině se částečná hrana nazývá coatback [32], [33], [34]. u intumescentních nátěrů není teplotní závislost tepelné vodivosti pevně stanovena, a to v důsledku jejich chemických reakcí a pěnění při zahřívání. Zjišťuje se chování nátěru a poté lze předpovědět množství pěnění. Efektivní tepelná vodivost se vyjadřuje ve zjednodušené formě v rovnici (1) [32].
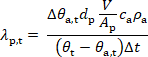 (1)
(1)
kde je
- λp,t
- tepelná vodivost [W/(m∙K)],
- Ap /V
- součinitel průřezu na metr [1/m],
- dp
- tloušťka ochranného materiálu [m],
- ca
- tepelná kapacita oceli [J/(kg∙K)],
- ρa
- hustota oceli [kg/m3],
- θt
- teplota plynu [°C],
- θa,t
- teplota oceli [°C],
- Δt
- časový interval t [s].
Při požáru intumescentní nátěry vytvoří několik vrstev, které mají různou tepelnou vodivost. Rovnice (1) nevyjadřuje přesný vztah mezi teplotou a tepelnou vodivostí povlaku. Z tohoto důvodu se dává přednost použití výsledků požárních zkoušek tenkých ochranných nátěrů a odvození základního vztahu mezi tepelnou vodivostí a teplotou z nich. Obr. 3 schematicky znázorňuje připojení vedlejšího nosníku, který je částečně chráněn před požárem, k hlavnímu nosníku, který je plně chráněn.
Kritická teplota oceli před ztrátou únosnosti se podle [35] pohybuje v rozmezí 580 °C až 750 °C. V případě stanovení rozsahu kritických teplot podle [36] se uvádí rozsah kritických teplot 498 až 1135 °C. Konečná kritická teplota ocelového prutu je ovlivněna poměrem zatížení, štíhlostí a účinkem bočních podpor. Východiska pro stanovení kritické teploty ocelových prvků uvedli Rubert a kol. [37] a porovnali je s novými poznatky z hlediska nerovnoměrného ohřevu [38]. Modelováním tepelného působení pomocí jmenovité standardní teplotní křivky je dána vztahem (2). Pokud se rovnice (2) nepoužije, uvažuje se při výpočtu teploty plynu vliv konvekce a radiace v rovnici (3).
kde je
- θg
- teplota plynu v blízkosti chráněného ocelového nosníku [°C],
- t
- čas [min].
Tepelný tok v počátku požáru je trojrozměrný, zejména v blízkosti připojení k hlavnímu nosnému prvku. v požárním úseku je sekundární nosník chráněn podle požadavků na požární ochranu. Předpokládá se, že celý obvod nechráněného prvku je rovnoměrně vystaven působení tepla. Tato idealizace je v souladu s předpokladem, že nosník působí jako prut. Prut je izolován ochranným materiálem v místě připojení k primárnímu prutu. Tepelný tok z povrchu lze vyjádřit jako průměrnou hodnotu. Tepelný tok procházející prutem vychází z Fourierova zákona vedení. Celkové teplo vstupující do diferenciálního objemu lze vyjádřit podle (3) [39].
kde je
- q(x)
- tepelný tok [W/m2],
- A(x)
- povrch [m2],
- ḣ
- součinitel přestupu tepla vedením v čase [W/(m2∙K)],
- A/V
- součinitel průřezu [1/m],
- θg
- teplota plynu [°C].
Zahrnutím závislosti tepelného toku na čase a v prvku lze rovnici (3) upravit takto (4):
kde je
- k
- tepelná vodivost [W/(m∙K)].
Parciální derivace druhého řádu v rovnici (4) je způsobena závislostí na čase a na teplotě. Úpravou rovnice (4) o tepelnou kapacitu c a hustotu ρ se upraví rovnice (5)–(8):
Kombinací rovnic (5) a (6) lze určit rovnici (7) v časové derivaci. Další úpravou lze získat rovnici (8), která zahrnuje vliv tepelné difúze, která je reprezentována K/cρ.
nebo
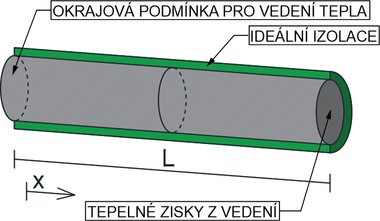
S dalšími úpravami přišli kolegové v [39]. Pro dosažení uzavřeného řešení podle rovnice (7) se uvažuje pouze délka izolovaného prvku; viz obr. 4. To znamená předpoklad, že konec prvku se po působení ohně náhle zahřeje na stejnou teplotu. Okrajové podmínky jsou tedy pro t = 0 a x = x, θ = θi je počáteční teplota nosníku. Pro t = 0 a x = 0, θ = θg dochází k rychlému nárůstu teploty na konci nosníku.
Diferenciální rovnici (7) lze řešit metodou konečných prvků nebo metodou konečných diferencí, případně metodou separace proměnných. Tvar tyče v kombinaci s okrajovými podmínkami naznačuje, že řešení lze vyjádřit pomocí již existujících mezilehlých řešení. Zvláštním tvarem tyče konečné délky se rozumí, že ji lze vytvořit společnými body ve vzájemně kolmém průsečíku nekonečné desky o tloušťce L a nekonečné tyče o obvodu PH a ploše A. Po dosazení do rovnice (8) lze tvar Φ vyjádřit v rovnici (9). Dosazením do rovnice (8) se získá tvar (10).
Okrajové podmínky se mění pro t = 0 a x = x na 𝛷 = θt − θg a pro t = 0 a x = 0 na Φ = 0. Pro hledané řešení (11), musí 𝛷1𝛷2 splňovat podmínky v rovnici (10). Po dosazení obou proměnných do rovnice (10) a jejich následné úpravě se získá rovnice (12).
Obě strany rovnice jsou funkcemi jedné proměnné a rovnají se proto konstantě. Rovnice (12) je funkcí všech hodnot, takže hodnoty v závorkách jsou nulové. Vztahy lze upravit na rovnice (13) až (17).
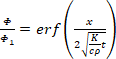 (15)
(15)
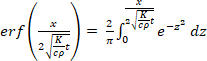 (16)
(16)
Výsledkem je vztah:
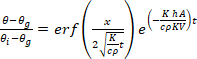 (18)
(18)
V rovnici (18), která v tomto případě uvažuje přidaný izolační materiál v ḣ, se K vztahuje k tepelné vodivosti oceli. Pro hranolovou tyč platí A/V = Hp /A, což je součinitel průřezu. Tloušťka požární ochrany se vypočítá z A/V = Hp /A prutu. Diferenciální řídicí rovnice je rovnice (18). Všechny parametry kromě délky požární ochrany jsou známy [39].
4. Závěr
Práce shrnuje způsoby pasivní ochrany ocelových konstrukcí se zaměřením na částečnou požární ochranu. Stávající vztahy byly upraveny pro průběh teploty v závislosti na čase. Byl vysvětlen analytické model návrhu částečné požární ochrany ocelových prutů.
Na tuto část navazuje část druhá představující experimenty a numerické modely. V druhé části jsou i představeny závěry ohledně použitelnosti částečné požární ochrany a poznatky při srovnání experimentu a numerických výstupů.
5. Literatura
- FERREIRA, F. A. & kol. A simplified method for assessing the temperature distribution in partially protected steel sections. Rem Revista Escola de Minas. 2007, 60(4), 645-655.
- DRURY, M. & kol. Structural fire resistance of partially restrained, partially composite floor beams, II: Modeling. Journal of Constructional Steel Research. 2020, 167. ISSN 0143974X. https://doi.org/10.1016/j.jcsr.2020.105946
- ZAHARIA, R. & kol. Numerical analysis of partially fire protected composite slabs. 2013, 14(1), 21-39. ISSN 1229-9367. https://doi.org/10.12989/scs.2013.14.1.021
- DAI, X. & kol. A Simple Method to Predict Temperatures in Steel Joints with Partial Intumescent Coating Fire Protection. Fire Technology. 2010, 46(1), 19-35. ISSN 0015-2684. https://doi.org/10.1007/s10694-009-0095-7
- WANG, P. & kol. Web-post buckling of fully and partially protected cellular steel beams at elevated temperatures in a fire. Thin-Walled Structures. 2016, 98, 29-38. ISSN 02638231. https://doi.org/10.1016/j.tws.2015.02.028
- WALD, F. & kol. On Bolted Connection with Intumescent Coatings. Proceedings of the Fourth International Workshop Structures in Fire. Aveiro: University of Aveiro, s. 371-377. ISBN 972-789-190-X.w
- MUNOZ-GARCIA, E. Analysis and Design Challenges and Solutions of 3 Sided Passive Fire Protection PFP on Steel Beam Decks for Offshore Installations. Day 4 Fri, March 25, 2016. OTC, 2016. https://doi.org/10.4043/26623-MS
- IMRAN, M. & kol. Thermal and Mechanical Response of Partially Protected Steel I-Beam under Fire. MATEC Web of Conferences. 2018, 203. ISSN 2261-236X. https://doi.org/10.1051/matecconf/201820306009
- HAUTALA, J. & kol. Resistance of partially protected steel beams in fire. Ce/papers. 2021, 4(2-4), 1849-1855. ISSN 2509-7075. https://doi.org/10.1002/cepa.1495
- WALD, F.; STREJČEK, M. Účinné vlastnosti požárně ochranných materiálů. Konstrukce. 2007, 6(5), 29-31. ISSN 1213-876.
- WANG, Y. C. & kol. Performance-based fire engineering of structures. 2012. Boca Raton: CRC Press, 2013. ISBN 978-0-415-55733-7.
- XIONG, M.-X. & kol. Modified Critical Temperatures for Steel Design Based on Simple Calculation Models in Eurocode 3. Fire Technology. 2017, 53(1), 227-248. ISSN 0015-2684. https://doi.org/10.1007/s10694-015-0522-x
- TUNCA, O. & kol. Structural features of cold-formed steel profiles. Challenge Journal of Structural Mechanics. 2018, 4(2), 77-81. ISSN 2149-8024. https://doi.org/10.20528/cjsmec.2018.02.005
- SINGH, R.; SAMANTA, A. Proposals for critical temperature of cold-formed steel compound sections under various load patterns. Asian Journal of Civil Engineering. 2022, 23(4), 609-633. ISSN 1563-0854.
https://doi.org/10.1007/s42107-022-00444-w - ŠEJNA, J. & kol. The partial fire protection of steel members: a comparative study. Journal of Structural Fire Engineering. 2023. ISSN 2040-2317. https://doi.org/10.1108/JSFE-01-2023-0001
- ŠEJNA, J. & kol. Increased Fire Resistance of a Steel Beam Using Oriented Standard Board Cladding – A Thermal Analysis. Proceedings of the 12th International Conference on Structures in Fire. Hong Kong: The Hong Kong Polytechnic University, 2022, s. 667-676.
- ŠEJNA, J.; BLESÁK, L. Požární odolnost dřevěných konstrukcí. Praha: Česká technika – nakladatelství ČVUT, 2022. ISBN 978-80-01-07012-3.
- TAMÁS-BÉNYEI, P.; SÁNTHA, P. Potential applications of basalt fibre composites in thermal shielding. Journal of Thermal Analysis and Calorimetry. ISSN 1388-6150. https://doi.org/10.1007/s10973-022-11799-2
- JONG, K. Y. & kol. Fire Resistance and Mechanical Properties of the Fire-Resistant Board. Advances in Material Science and Engineering. Singapore: Springer Singapore, 2021, 249-256. Lecture Notes in Mechanical Engineering. ISBN 978-981-16-3640-0. https://doi.org/10.1007/978-981-16-3641-7_29
- YANG, W. & kol. A New, Green, Recyclable Fireproof Insulation Board for Use in Integrated Composite Structure Fire Protection Systems. Fire. 2022, 5(6). ISSN 2571-6255. https://doi.org/10.3390/fire5060203
- ČELKO, L. & kol. Durability of Amorphous and Crystalline BMAS Thermal Barrier Coatings Produced by Plasma Spraying. Solid State Phenomena. 2016, 258, 383-386. ISSN 1662-9779. https://doi.org/10.4028/www.scientific.net/SSP.258.383
- JO, H. & kol. Multi-layer barrier coating technology using nano-fibrillated cellulose and a hydrophobic coating agent. BioResources. 2022, 17(4), 6222-6233. ISSN 19302126. https://doi.org/10.15376/biores.17.4.6222-6233
- LI, Q. & kol. Accurate 3D thermal stress analysis of thermal barrier coatings. International Journal of Mechanical Sciences. 2022, 217. ISSN 00207403. https://doi.org/10.1016/j.ijmecsci.2021.107024
- SUZUKI, M. & kol. The Current Status of Environmental Barrier Coatings and Future Direction of Thermal Spray Process. MATERIALS TRANSACTIONS. 2022, 63(8), 1101-1111. ISSN 1345-9678.
https://doi.org/10.2320/matertrans.MT-T2021003 - VAGGE, S. T.; GHOGARE, S. Thermal barrier coatings: Review. Materials Today: Proceedings. 2022, 56, 1201-1216. ISSN 22147853. https://doi.org/10.1016/j.matpr.2021.11.170
- FAN, C. & kol. Effect of ambient wind on the flame retardancy of intumescent coatings. Journal of Thermal Analysis and Calorimetry. ISSN 1388-6150. https://doi.org/10.1007/s10973-022-11593-0
- LUCHERINI, A. & kol. Numerical heat transfer model for swelling intumescent coatings during heating. International Journal of Thermal Sciences. 2023, 184. ISSN 12900729. https://doi.org/10.1016/j.ijthermalsci.2022.107922
- AZMI, Y. & kol. Investigating the Mechanical Performance of Intumescent Coating Enhanced with Magnesium Oxide (MgO) for Structural Steel Application. ICPER 2020. Singapore: Springer Nature Singapore, 2022, 927-938. Lecture Notes in Mechanical Engineering. ISBN 978-981-19-1938-1. https://doi.org/10.1007/978-981-19-1939-8_69
- PIPEROPOULOS, E. & kol. Study of Intumescent Coatings Growth for Fire Retardant Systems in Naval Applications: Experimental Test and Mathematical Model. Coatings. 2022, 12(8). ISSN 2079-6412.
https://doi.org/10.3390/coatings12081180 - ŠEJNA, J. & kol. Application of hybrid cement in passive fire protection of steel structures. Journal of Structural Fire Engineering. 2023. ISSN 2040-2317. https://doi.org/10.1108/JSFE-01-2023-0007
- HÄßLER, D.; HOTHAN, S. Performance of intumescent fire protection coatings applied to structural steel tension members with circular solid and hollow sections. Fire Safety Journal. 2022, 131. ISSN 03797112.
https://doi.org/10.1016/j.firesaf.2022.103605 - PODOLSKI, D. & kol. Applications of Fire Engineering: Numerical investigation of intumescent ‘coatback’ on unprotected secondary beams. The University of Manchester, 2017, (1), 10. ISSN 9781315107202.
https://doi.org/10.15127/1.309552 - BREUNESE, A. A Simple Method for Calculation of Coat Back Lengths. PROMAT. 2019, 2019, 1-9.
- VOROSIN, A. O.; PARFENENKO, A. P. The research into the heating effect of secondary steel structures, having no fire proofing, on the fire resistance of fireproof steel beams. Pozharovzryvobezopasnost/Fire and Explosion Safety. 2021, s. 16-30. ISSN 2587-6201. https://doi.org/10.22227/0869-7493.2021.30.03.16-30
- BS5950. Structural use of steelwork in building: Part 1. Code of practice for design in simple and continuous construction: hot rolled sections. 1. UK: British Standard, 1990.
- EN 1993-1-2. Eurocode 3: Design of steel structures - Part 1-2: General rules - Structural fire design. 1. EU: The European Union Per Regulation, 2005.
- RUBERT, A.; SCHAUMANN, P. Critical temperatures of steel columns exposed to fire. Fire Safety Journal. 1988, 13(1), 39-44. ISSN 03797112. https://doi.org/10.1016/0379-7112(88)90031-8
- NGUYEN, X. & kol. Numerical Investigation on Critical Temperature of Steel I-Beams Under Non-uniform Heating Condition—Comparison with Eurocode 3. Computational Intelligence Methods for Green Technology and Sustainable Development. Cham: Springer International Publishing, 2023, 282-290. Lecture Notes in Networks and Systems. ISBN 978-3-031-19693-5. https://doi.org/10.1007/978-3-031-19694-2_25
- YASSERI, S. F. Coat-Back Length: In Passive Fire Protection of Offshore Installations. 21st International Conference on Offshore Mechanics and Arctic Engineering, Volume 2. ASMEDC, 2002, 621-627. ISBN 0-7918-3612-6.
https://doi.org/10.1115/OMAE2002-28537
Poděkování
Tento výsledek byl realizován za finanční podpory z prostředků grantu ČVUT SGS22/141/OHK1/3T/11 „Bezpečnost a udržitelnost dřevěných a ocelových konstrukcí vystavených požáru“.
V článku jsou shrnuty teoretické poznatky o současných metodách používaných pro částečnou požární ochranu ocelových konstrukcí. Částečná ochrana spočívá v ochraně hlavních prvků konstrukce (např. u stropních konstrukcí s nechráněnými stropnicemi se teplo přenáší vedením do spojů a průvlaků díky dobré tepelné vodivosti oceli, částečné požární ochrany se využívá například pro stropnice v oblasti spoje, omezí se přenos tepla). Jsou uvedeny analytické a matematické metody, které jsou vhodné pro stanovení tepelných vlastností a požární odolnosti používaných materiálů. Článek uvádí i stručný přehled pasivních ochranných systémů pro ochranu ocelových konstrukcí (nátěry, nástřiky, obklady).
Autoři v článku objasňují tzv. analytický model návrhu částečné požární ochrany ocelových prutů.
Článek poskytuje základ pro pokračování (2. část článku), kde by měly být představeny závěry ohledně použitelnosti částečné požární ochrany a poznatky při srovnání experimentu a numerických výstupů.
Závěr: článek doporučuji k vydání. Pokud by to bylo technicky možné, doporučoval bych vydání obou částí článku společně.
This article focuses on the partial fire protection of steel structures and provides a theoretical review of current methods and materials used in this area. Various types of passive fire protection systems are introduced, including intumescent coatings and their influence on heat transfer between protected and unprotected parts of the structure. The article deals with analytical and mathematical methods for determining the thermal properties and fire resistance of the materials used, with an emphasis on those that undergo thermal degradation. This article offers a comprehensive view of the theoretical foundations of partial fire protection of steel structures and proposes directions for further research in this area, providing a basis for Part 2: Experiments, Numerical Models, and Comparisons.