Reklama

Tepelné ztráty způsobené dešťovým odpadním potrubím

23.9.2013

Ing. Jakub Vrána, Ph.D., VUT Brno, Ústav TZB, Ing. Vladimír Valenta

Recenzovaný

V chladném období odtéká dešťovým odpadním potrubím studená dešťová voda, která s sebou strhává studený venkovní vzduch. Je nutné, z důvodu tepelných ztrát a zabránění kondenzace na vnějším povrchu trub, dešťová odpadní potrubí vedená uvnitř budovy tepelně izolovat?

Reklama

Dešťová odpadní potrubí jsou svislá potrubí, která odvádějí dešťovou vodu ze střech. Mohou se na nich vyskytnout i ležaté úseky, vedené např. pod stropem. Při průtoku dešťových vod je do odpadního potrubí strháván venkovní vzduch. Pokud dešťová voda neprotéká, proudí dešťovým odpadním potrubím vzduch z kanalizace nad střechu. Výjimkou jsou dešťová odpadní potrubí, např. z teras, opatřená v nejnižším podlaží zápachovou uzávěrkou, která proudění vzduchu z kanalizace zabraňuje. V místě vstupu do odpadního potrubí (v jeho nejnižší části) má při napojení domu na kanalizaci pro veřejnou potřebu vzduch i v zimním období teplotu nad bodem mrazu. Pokud dešťová vnitřní kanalizace ústí do venkovního prostoru (do povrchových vod, na terén apod.), může být teplota v místě vstupu do dešťového odpadního potrubí (v jeho nejnižší části) přibližně rovna venkovní teplotě. V chladném období odtéká dešťovým odpadním potrubím studená dešťová voda, která s sebou strhává studený venkovní vzduch. Teplota dešťové vody i vzduchu je v místě vstupu do potrubí (v jeho nejvyšší části) přibližně rovna venkovní teplotě.

Na základě výše uvedených skutečností si řada projektantů zdravotně technických instalací klade otázku, zda je nutné, z důvodu tepelných ztrát a zabránění kondenzace na vnějším povrchu trub, dešťová odpadní potrubí vedená uvnitř budovy tepelně izolovat.

V příspěvku je uveden způsob stanovení tepelné ztráty ve vnitřním prostředí od dešťového odpadního potrubí, které odvádí dešťové vody ze střech a prochází tímto prostředím. Po celou dobu, kdy dešťová voda není odváděna, proudí odpadním potrubím vzhůru vzduch. Tím jsou ochlazovány prostory uvnitř budovy. Způsob určení tepelné ztráty vychází ze stanovení rychlosti vzduchu proudícího uvnitř dešťového odpadního potrubí. Z rychlosti vzduchu je možné dále vypočítat průběh teplot vzduchu uvnitř odpadního potrubí a nakonec i tepelné ztráty způsobené dešťovým odpadním potrubím.

Výtok z potrubí může ústit buď do volného prostoru, nebo do ležatého svodného potrubí napojeného na kanalizaci pro veřejnou potřebu.

Průtok dešťové vody odpadním potrubím

Doba, kdy je dešťová voda sváděna potrubím ze střechy, je poměrně krátká, takže nemá na klima uvnitř budovy prakticky vliv. Pouze na vnějším povrchu potrubí, pokud není potrubí izolováno, může kondenzovat vlhkost. Je to v případě, když teplota na vnějším povrchu potrubí klesne pod teplotu rosného bodu vzduchu v prostředí obklopujícím dešťové odpadní potrubí (tab. 1). Je patrné, že např. při teplotě vnitřního prostředí t_p = 20 °C nastane kondenzace na vnějším povrchu potrubí při teplotě dešťové vody t_d ≤ 12 °C. Tato úvaha platí pro případ, kdy je tepelný odpor stěny potrubí nízký. Je-li potrubí tepelně izolováno, kondenzace se neprojeví.

Tab. 1 Podmínky pro kondenzaci vlhkosti na vnějším povrchu dešťového odpadního potrubí
Teplota vnitřního prostředí `t`_p [°C]	15	20	25
Teplota rosného bodu vnitřního vzduchu `t`_rb [°C]	7	12	17
Kondenzace vlhkosti nastane při teplotě dešťové vody `t`_d ≤ `t`_rb.
Teplota rosného bodu vnitřního vzduchu je určena pro relativní vlhkost `φ` = 60 %.

Průtok vzduchu dešťovým odpadním potrubím

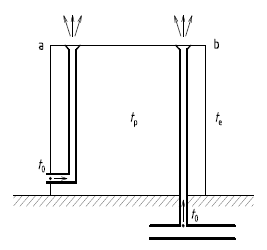
Obr. 1 Druhy dešťových odpadních potrubí s průtoky vzduchu;
a) výtok zaústěný do volného prostoru,
b) výtok zaústěný do ležatého svodného potrubí kanalizace

Zde si popíšeme výchozí poznatky potřebné pro pozdější výpočty. V době, kdy dešťovým odpadním potrubím neodtéká dešťová voda, bude jím stoupat vzduch. Bude přisáván vztlakem buď z vnějšího prostředí, nebo ze svodného potrubí kanalizace (obr. 1). Teplota vzduchu vstupujícího do dešťového odpadního potrubí t₀ (°C) bude v prvním případě shodná s vnější teplotou. Ve druhém případě bude tato teplota těsně nad 0 °C při venkovní teplotě −12 °C a 10 °C při venkovní teplotě 20 °C a vyšší.

Vztlak vzduchu v dešťovém odpadním potrubí [Pa] je dán vztahem:

Δp_v = h × g × Δρ (1)

kde je

h: – výška dešťového odpadního potrubí [m]
g: – zemské zrychlení = 9,81 [m.s⁻²]
Δρ: – rozdíl hustot vzduchu = ρ_e − ρ_i [kg.m⁻³]
ρ_e: – hustota vnějšího vzduchu při teplotě t_e [kg.m⁻³]
ρ_i: – hustota vzduchu ve svodu při střední teplotě t_i [kg.m⁻³].

Tlaková ztráta [Pa] při proudění vzduchu dešťovým odpadním potrubím je dána vztahem:

Δp_z = { λ × (h / D) + ζ } × 0,5 × v² × ρ (2)

kde je

λ: – součinitel tření v potrubí [–]
D: – vnitřní průměr potrubí [m]
ζ: – součinitel místního odporu [–]
v: – rychlost proudění vzduchu v potrubí [m.s⁻¹]
ρ: – hustota vzduchu ve vstupu do potrubí [kg.m⁻³]

Při proudění vzduchu dešťovým odpadním potrubím nastane rovnováha mezi vztlakem a tlakovou ztrátou. Z rovnosti vztahů (1) a (2) lze za zjednodušujících předpokladů zkontrolovat rychlost proudění vzduchu dešťovým odpadním potrubím.

Jedná se o tři následující předpoklady:

1. Předběžně zvolíme střední teplotu vzduchu v odpadním potrubí ve výši t_i = t₀ + 0,25 . (t₀ + t_p). Pro tuto teplotu odečteme z tabulek hustotu vzduchu v odpadním potrubí ρ_i [kg.m⁻³]. Všechny zde uváděné hustoty vzduchu platí pro tlak 101,3 kPa.

2. Předpokládáme, že součinitel tření v potrubí bude konstantní ve výši λ = 0,05. Ten byl stanoven pomocí Reynoldsova kritéria Re pro rychlost proudění vzduchu v potrubí v = 1 m.s⁻¹, vnitřní průměr potrubí D = 0,1 m pro kinematickou viskozitu vzduchu ν = 14.10⁻⁶ m².s⁻¹ při teplotě 0 °C. Hodnota Reynoldsova kritéria [–] je dána vztahem:

Re = v × D / ν (3)

Pro uvedené hodnoty bude hodnota Reynoldsova kritéria:

Re = 1 × 0,1 / 14×10⁻⁶ = 7 000

Ze známého diagramu λ = f (Re; e/D), kde e/D je poměrná drsnost potrubí [–] a e je drsnost potrubí [m], lze pro Re = 7 000 a pro e/D = 0,01 odečíst právě hodnotu součinitele tření v potrubí λ = 0,05.

3. Upravíme obsah mezi závorkami { λ × (h/D) + ζ } ze vztahu (2) na tvar a × λ × (h/D), kde součinitel a [–] umožňuje nahradit součet veličin mezi závorkami, a tím i součinitel místního odporu ζ. Hodnota bývá a = 1,2.

Rychlost proudění vzduchu [m.s⁻¹] dešťovým odpadním potrubím potom bude dána hledaným vztahem:

v = { 2 × D × g × Δρ / (a × λ × ρ_i) }^0,5 (4)

Pomocí tohoto vztahu zkontrolujeme, zda je rychlost proudění vzduchu dešťovým odpadním potrubím přibližně shodná s předpokládanou rychlostí v = 1 m.s⁻¹. Pokud ano, znamená to, že hodnota kritéria Re se zásadně nemění, takže se nezmění ani hodnota součinitele tření v potrubí λ = 0,05. Jinak je nutné výpočet vztahů (3) a (4) opakovat (zpřesnit) pro vypočítanou rychlost vzduchu.

Příklad 1

Zadání

Pro vnitřní neizolované dešťové odpadní potrubí zaústěné do kanalizačního svodného potrubí máme stanovit rychlost proudění vzduchu. Dešťové odpadní potrubí má vnitřní průměr D = 0,1 m a výšku h = 10 m. Teplota vnitřního prostředí t_p = 20 °C a hustota vnějšího vzduchu při teplotě −12 °C je ρ_e = 1,353 kg.m⁻³. Dále je součinitel a = 1,2 a součinitel tření v potrubí λ = 0,05.

Řešení

Střední teplota vzduchu v dešťovém odpadním potrubí je

t_i = t₀ + 0,25 × (t₀ + t_p) = 0 + 0,25 × (0 + 20) = 5 °C.

Této teplotě odpovídá hustota vzduchu ρ_i = 1,270 kg.m⁻³.
Rozdíl hustot vzduchu Δρ = ρ_e − ρ_i = 1,353 − 1,270 = 0,083.
Rychlost proudění vzduchu dešťovým odpadním potrubím je dána vztahem (4), takže:

v = { 2 × 0,1 × 9,81 × 0,083 / (1,2 × 0,05 × 1,270) }^0,5 = 1,46 m.s⁻¹.

Tato rychlost změní hodnotu Reynoldsova kritéria ze 7 000 na 10 220. Z nové hodnoty Re vyplývá i nový součinitel tření v potrubí λ = 0,043.

Zpřesněná rychlost proudění vzduchu dešťovým odpadním potrubím je také dána vztahem (4), takže:

v = { 2 × 0,1 × 9,81 × 0,083 / (1,2 × 0,043 × 1,270) }^0,5 = 1,57 m.s⁻¹.

Tuto rychlost proudění vzduchu dešťovým odpadním potrubím můžeme považovat za reálnou.

Teploty vzduchu při průtoku dešťovým odpadním potrubím

Z řešení diferenciální rovnice pro předávání tepla z vnitřního prostředí budovy o teplotě t_p do vzduchu proudícího dešťovým odpadním potrubím získáme vztah pro teplotu vzduchu t₁ [°C] na jeho vrcholu:

t₁ = t_p − e^−b.h × (t_p − t₀) (5)

kde je

b: – součinitel daný vztahem (6) [m⁻¹]
t₀: – teplota vzduchu na vstupu do odpadního potrubí [°C]

Součinitel b [m⁻¹] je dán vztahem:

b = U / (900 × c × v × D) (6)

kde je

U: – součinitel prostupu tepla z vnitřního prostředí budovy do vzduchu v odpadním potrubí [W.m⁻².K⁻¹]
c: – měrná tepelná kapacita vzduchu při 0 °C = 0,35 [Wh.m⁻³.K⁻¹]

Příklad 2

Zadání

Máme stanovit teplotu vzduchu na vrcholu neizolovaného dešťového odpadního potrubí zaústěného do kanalizačního svodného potrubí o parametrech podle příkladu 1. Součinitel prostupu tepla z vnitřního prostředí do vzduchu v neizolovaném odpadním potrubí U = 4 W.m⁻².K⁻¹.

Řešení

Nejprve vypočítáme součinitel b ze vztahu (6), takže:

b = 4 / (900 × 0,35 × 1,57 × 0,1) = 0,081 m⁻¹.

Dále vypočítáme teplotu vzduchu na vrcholu odpadního potrubí dle vztahu (5):

t₁ = 20 − e^−0,081.10 × (20 − 0) = 11 °C.

Střední teplota vzduchu v odpadním potrubí bude:

t_i = 0,5 × (t₁ + t₀) = 0,5 × (11 + 0) = 5,5 °C.

Protože předpokládaná střední teplota vzduchu v odpadním potrubí (příklad 1) byla t_i = 5 °C a vypočítaná je t_i = 5,5 °C, což je téměř ve shodě, lze považovat dosavadní výsledky řešení za správné.

Tepelné ztráty od dešťových odpadních potrubí

Tepelná ztráta od neizolovaného dešťového odpadního potrubí [W] je dána vztahem:

Q = α_p × π × D × h × (t_p − t_i) (7)

kde je

α_p: – součinitel přestupu tepla ze vzduchu prostředí na povrch odpadního potrubí = 8 [W.m⁻².K⁻¹]

Pro jednoduchost se předpokládá, že povrchová teplota odpadního potrubí je totožná se střední teplotou vzduchu v odpadním potrubí a vnější průměr potrubí je shodný s jeho vnitřním průměrem D.

Tepelná ztráta od izolovaného dešťového odpadního potrubí [W] je dána vztahem:

Q = U × π × D × h × (t_p − t_i) (8)

kde je

U: – součinitel prostupu tepla ze vzduchu prostředí do vzduchu v odpadním potrubí [W.m⁻².K⁻¹].

Opět pro jednoduchost se předpokládá, že se teplo tepelnou izolací šíří jednorozměrně.

Součinitel prostupu tepla ze vzduchu prostředí do vzduchu v odpadním potrubí (W.m⁻².K⁻¹) je potom dán vztahem:

U = 1 / { (1 / α_p) + (s / λ_s) + (1 / α_i) } (9)

kde je

s: – tloušťka tepelné izolace potrubí [m]
λ_s: – součinitel tepelné vodivosti tepelné izolace [–]
α_i: – součinitel přestupu tepla z vnitřního povrchu odpadního potrubí do vzduchu uvnitř potrubí = 8 [W.m⁻².K⁻¹]

Příklad 3

Zadání

Máme stanovit tepelnou ztrátu od dešťového odpadního potrubí o parametrech podle příkladů 1 a 2. Nejprve neizolovaného potrubí a poté potrubí izolovaného. Tepelná izolace má tloušťku s = 0,02 m a součinitel tepelné vodivosti λ_s = 0,05.

Řešení

Tepelná ztráta od neizolovaného dešťového odpadního potrubí je dána vztahem (7), takže:

Q = 8 × π × 0,1 × 10 × (20 − 5,5) = 364 W.

Součinitel prostupu tepla ze vzduchu prostředí do vzduchu v odpadním potrubí je dán vztahem (9), takže:

U = 1 / { (1/8) + (0,02 / 0,05) + (1/8) } = 1,54 W.m⁻².K⁻¹.

Tepelná ztráta od izolovaného dešťového odpadního potrubí [W] je dána vztahem (8), takže:

Q = 1,54 × π × 0,1 × 10 × (20 − 5,5) = 70,2 W.

Vidíme, že poměrně tenkou tepelnou izolací na potrubí klesne tepelná ztráta od izolovaného dešťového odpadního potrubí na pětinu oproti potrubí neizolovanému. Tepelná izolace dešťových odpadních potrubí je nutná u domů s nízkou potřebou tepla na vytápění.

Závěr

V době, kdy je dešťová voda sváděna neizolovaným potrubím ze střechy, téměř vždy dochází ke kondenzaci vlhkosti na vnějším povrchu potrubí. Teplota povrchu, daná teplotou dešťové vody, totiž klesne pod teplotu rosného bodu vzduchu vnitřního prostředí.

V době, kdy není sváděna dešťová voda, proudí dešťovým odpadním potrubím vzhůru vzduch. Ten způsobuje znatelné tepelné ztráty pro vnitřní prostředí.

Oba uvedené jevy je nutné omezit tepelnou izolací. Přitom postačí poměrně tenká izolace o tloušťce s = 20 mm se součinitelem tepelné vodivosti λ_s ≤ 0,05.

English Synopsis

Heat loss from the rain drain pipe

In the cold season flows rain drain pipe cold rainwater posed pulls cold outside air. It is necessary due to heat loss and to prevent condensation on the outer surface of pipes, rainwater pipes led inside thermally insulate buildings?