Ověření spolehlivosti existujícího železobetonového prvku
Příklad ověření spolehlivosti existujícího železobetonového prvku navazuje na předchozí článek autora „Nový evropský dokument pro hodnocení existujících konstrukcí“. Ilustrativní příklad ověření jednoduchého železobetonového prvku se opírá o připravovaný evropský dokument (technickou specifikaci TS [2]) a platné Eurokódy ČSN EN 1990 [7] a ČSN EN 1991-1-1 [9]. Příklad doplňuje předchozí článek, je usnadnit očekávané uvedení připravovaného evropského dokumentu do soustavy národních norem pro hodnocení existujících konstrukcí.
1. Zadání
Existující obytná panelová budova postavená v roce 1970 prochází úpravou a předpokládané přitížení vyžaduje ověření její spolehlivosti. Ověření lze omezit na prostě uložený železobetonový panel (prefabrikovaný stropní panel tloušťky h = 0,19 m a účinné výšce d = 0,16 m) o rozpětí L = 6 m, podle dostupné dokumentace je dále známo, že návrhová hodnota ohybové únosnosti přepočtené na (b =) 1 m šířky panelu činí Rd = 37,59 kNm. Předpokládá se jakost betonu C20/25 (B20) a přesnost provedení panelu odpovídající prefabrikované výrobě. S ohledem na tyto vlastnosti panelu lze minimální plochu výztuže odhadnout hodnotou As = 0,00058 m2. Základní veličiny popisující odolnost panelu jsou tedy: As = 0,00058 m, d = 0,16 m, b = 1 m, fck = 20 MPa, fyk = 500 MPa.
Panel má přenášet stálé zatížení (včetně nových vrstev podlahy) gk = 6,264 kN/m2 a užitné zatížení qk = 1,5 kN/m2 (ČSN EN 1991-1-1 [9]). Požaduje se zbytková životnost panelu 50 let a směrná úrovně spolehlivosti odpovídající indexu spolehlivosti β = 3,8 pro referenční dobu stejnou jako zbytková životnost (50 let). Směrná úroveň spolehlivosti stanovená indexem spolehlivosti β = 3,8 pro referenční dobu 50 let však může být přizpůsobena skutečným ekonomickým a sociálním podmínkám (zpravidla se snižuje).
Čtěte také Nový evropský dokument pro hodnocení existujících konstrukcí
2. Metoda dílčích součinitelů
2.1 Dílčí součinitele doporučené v Eurokódech
Počáteční metodou ověřování je zpravidla metoda dílčích součinitelů s využitím hodnot součinitelů γ podle platných norem (ČSN EN 1990 [7]). Tento první orientační krok využívá známé postupy a nevyžaduje žádné statistické metody a pravděpodobnostní úvahy. Často však vede k negativním výsledkům a ukazuje na požadavek uplatnění výstižnějších a zpravidla složitějších postupů ověřováni spolehlivosti.
Tab. 1 uvádí dílčí charakteristické hodnoty a součinitele γ pro zatížení doporučené v ČSN EN 1990 [7] a pro odolnost betonové konstrukce odhadnuté pro ohyb betonové konstrukce společně se stanovenými (návrhovými) hodnotami zatížení a odolnosti. Uvedené hodnoty odpovídají indexu spolehlivosti β = 3,8 vztaženému k referenční době 50 let. Nepřihlížejí však ke skutečným podmínkám hodnocené konstrukce (specifickým vlastnostem zatížení a odolnosti).
| Veličiny | g [kN/m2] | q [kN/m2] | fck [MPa] | fyk [MPa] |
|---|---|---|---|---|
| Charackter. hodnoty | 6,264 | 1,5 | 20 | 500 |
| Součinitele | 1,35 | 1,5 | 1,5 | 1,15 |
| Stanovené hodnoty | 8,456 | 2,25 | 13,33 | 435 |
| Stanovené Ea a Ra [kNm] | 48,18 | 37,59 | ||
Odhadnutá hodnota účinku zatížení Ea = 48,18 kNm překračuje stanovenou hodnotu odolnosti Ra = 37,59 kNm (Ea > Ra), a použitá metoda s dílčími součiniteli obecně doporučenými v Eurokódech (ČSN EN 1990 [7] a ČSN EN 1992-1-1 [9]) spolehlivost panelu nepotvrzuje.
2.2 Přizpůsobené dílčí součinitele
Dílčí součinitele γ lze v odůvodněných případech přizpůsobit (zpravidla snížit) vzhledem ke skutečným podmínkám konstrukce, jak naznačují rovnice (6.3), (6.4). Uplatňuje se ohled na variační koeficienty vlastností hodnocené konstrukce, na stanovenou směrnou úroveň spolehlivosti β = 3,8 a na součinitele citlivosti αE a αR, jejichž doporučené hodnoty αE = −0,7 a αR = 0,8 (v ČSN EN 1990 [7]) se mohu přizpůsobit. Pro hodnocený panel tab. 2 uvádí stanovené dílčí součinitele γ pro základní veličiny g, q, fck a fyk (přizpůsobené modelovým nejistotám a variabilitě rozměrů) a stanovené hodnoty účinku zatížení Ea a odolnosti Ra.
| Veličiny | g [kN/m2] | q [kN/m2] | fck [MPa] | fyk [MPa] |
|---|---|---|---|---|
| Charackter. hodnoty | 6,264 | 1,5 | 20 | 500 |
| Součinitele | 1,15 | 1,4 | 1,4 | 1,1 |
| Stanovené hodnoty | 8,204 | 2,10 | 14,29 | 455 |
| Stanovené Ea a Ra [kNm] | 41,87 | 39,75 | ||
Odhadnutá hodnota účinku zatížení Ea = 41,87 kNm je mírně převyšuje stanovenou hodnota odolnosti Ra= 39,75 kNm (Ea > Ra) a spolehlivost panelu není tedy ani s využitím přizpůsobených dílčích součinitelů γ potvrzena.
Přizpůsobené dílčí součinitele γ se stanoví na základě vztahů (6.3) a (6.4) a zásad uvedených v normě ČSN EN 1990 ([7], [8]). Úprava dílčích součinitelů vyžaduje stanovení statistických charakteristik základních veličin a jejich rozdělení. Předpokládaná rozdělení základních veličin g, q a R jsou stanovena v souladu s poznatky uvedenými v literatuře ([11], [12] a [13]). Normální rozdělení se obvykle předpokládá pro stálá zatížení. Gumbelovo a lognormální rozdělení se zpravidla aplikují pro proměnná zatížení, lognormální rozdělení pro veličiny odolnosti. Určení výstižného rozdělení základních veličin však vyžaduje dostatek dat a jejich statistické vyhodnocení. Rozhodující vlastností pro výstižný popis veličin je zpravidla variační koeficient v kombinaci s momentem třetího řádu (šikmostí nebo asymetrií).
Variační koeficienty V mají zpravidla zahrnovat kromě variability základních veličin také variabilitu geometrických parametrů a odpovídající modelovou nejistotu (je-li to nutné) podle jednoduchého vztahu
Symbol Vi označuje variační koeficient základní veličiny i, Vgeo variační koeficient odpovídajících geometrických parametrů a Vunc variační koeficient případných modelových nejistot. Variační koeficient odolnosti R závisí u hodnoceného prvku pouze na vyztužení.
Variační koeficienty a dílčí součinitele uvedené v tab. 3 jsou poměrně nízké, odpovídají však podmínkám hodnocené prefabrikované konstrukce a hodnotám použitým v původním návrhu konstrukce. Nicméně, podobně jako v předchozím případě ověřování metodou dílčích součinitelů podle ČSN EN 1990 [7], stanovený účinek zatížení Ea = 41,87 kNm je větší než odolnost Ra = 37,59 kNm. Spolehlivost panelu tedy není potvrzena ani úpravou dílčích součinitelů. Náročnější metoda upravených dílčích součinitelů sice poskytuje mírně příznivější výsledek než užití neupravených dílčích součinitelů, přesto však nepotvrzuje dostatečnou spolehlivost panelu.
3. Metoda stanovených hodnot
Metoda stanovených hodnot je vyjádřena rovnicí (6.5). Její podstatou je přímé stanovení (návrhových) hodnot na základě směrné hodnoty indexu spolehlivosti β = 3,8 (pro požadovanou zbytkovou životnost 50 let) a součinitelů citlivosti veličin popisujících relativní vliv zatížení a odolnost αE = −0,7 a αR = 0,8. Hodnoty základních veličin a účinku zatížení Ea a odolnosti konstrukce Ra jsou tedy určeny bez užití dílčích součinitelů γ. Nutné je však znát teoretické modely rozdělení všech základních veličin g, q, fc a fy včetně jejich skutečných charakteristik, průměru μX, směrodatné odchylky σX nebo variačního koeficientu VX. Tyto informace jsou uvedeny v tab. 3, která uvádí typ rozdělení a požadované statistické charakteristiky základních veličin i stanovené hodnoty účinku zatížení Ea a odolnosti Ra.
| Veličiny | g [kN/m2] | q [kN/m2] | fck [MPa] | fyk [MPa] |
|---|---|---|---|---|
| Charakter. hodnoty xk | 6,264 | 1,5 | 20 | 500 |
| Průměr μX | 6,264 | 0,9 | 28 | 580 |
| Variační koeficient VX | 0,05 | 0,35 | 0,10 | 0,05 |
| Směrodatná odchylka σX | 0,63 | 0,315 | 2,8 | 29 |
| Předpokládané rozdělení | Normal | Gumbel | Lognormal | Lognormal |
| Součinitel αE a αR | −0,7 | −0,7 | 0,8 | 0,8 |
| Redukovaný index βαE a βαR | −2,66 | −2,66 | 3,04 | 3,04 |
| Poměr ~ xa/μX | 1,15 | 2,36 | 0,70 | 0,82 |
| Stanovené hodnoty xa | 7,20 | 2,12 | 19,60 | 476 |
| Celkové zatížení [kN/m2] | 9,32 | – | ||
| Stanovené Ea a Ra [kNm] | 41,40 | 42,22 | ||
Stanovená výsledná hodnota účinku zatížení Ea = 41,40 kNm v tomto případě nepřekračuje menší hodnotu odolnosti Ra = 42,22 kNm, Ea < Ra, což ověřuje, že panel lze považovat za dostatečně spolehlivý. Metoda stanovených hodnot je zpravidla příznivější než metody dílčích součinitelů, které jsou zatíženy konzervativními předpoklady přijatými při určení dílčích součinitelů a při specifikaci výchozích charakteristických hodnot. V obou případech jsou doporučené hodnoty na straně bezpečnosti.
Dále je vhodné poznamenat, že šikmost Gumbelova rozdělení je poměrně vysoká (1,14), což nemusí odpovídat skutečnému rozdělení užitného zatížení q v obytných prostorách. Alternativně lze předpokládat lognormální rozdělení, které může být výstižnější. Při použití Gumbelova rozdělení pro zatížení q je stanovená hodnota zatížení Ea = 41,40. Jestliže se předpokládá lognormální rozdělení s počátkem v nule a menší šikmostí (1,05), je výsledná hodnota zatížení Ea = 40,30 kNm a výsledek je ještě mírně příznivější.
4. Pravděpodobnostní metoda
Pravděpodobnostní ověřování existujících konstrukcí vychází z rovnice (6.7). Předpokládá se, že všechny základní veličiny Xi lze považovat za náhodné veličiny, které lze popsat vhodným rozdělením pravděpodobnosti. V případě hodnoceného stropního panelu jsou tři základní veličiny g, q a R již dostatečně popsány v předchozím oddílu. Spolehlivost konstrukce se obecně ověřuje prostřednictvím pravděpodobnosti poruch stanovené na základě funkcí mezního stavu g(Xi), kde symboly Xi označují základní veličiny. V případě hodnoceného stropního panelu o rozpětí L = 6 m (považovaného za deterministickou veličinu) je funkce mezního stavu dána vztahem
Ve smyslu rovnice (6.7) se předpokládá, že porucha nastane, jestliže funkce mezního stavu je negativní (odolnost R je nedostatečná), tedy jestliže platí
Jestliže funkce mezního stavu je pozitivní, g(Xi) ≥ 0, pak se předpokládá, že k poruše panelu nedojde.
Podle oddílu 6.4 se konstrukce se považuje za spolehlivou, pokud pravděpodobnost poruchy Pf je menší než směrná hodnota pravděpodobnosti Pft nebo index spolehlivosti β je větší než směrná hodnota indexu βt a splňuje tedy podmínku:
Předpokládané (aktualizované) modely základních veličin jsou přehledně uvedeny v tab. 4. Uvedené modely jsou stanoveny na základě aktualizace apriorních modelů s výsledky nových experimentálních informací získaných v průběhu podrobného vyšetřování hodnocené konstrukce.
| Veličina | Symbol | Jednotka | Charakteristická h. | Rozdělení | Průměr | Směrod. odchylka | Variační koeficient |
|---|---|---|---|---|---|---|---|
| Plocha výztuže | As | m2 | 0,00058 | DET | 0,00058 | – | – |
| Účinná výška | d | m | 0,16 | N | 0,16 | 0,005 | 0,06 |
| Šířka průřezu | b | m | 1 | N | 1 | 0,02 | 0,02 |
| Rozpětí panelu | L | m | 6 | DET | 6 | – | – |
| Mez kluzu | fy | MPa | 500 | LN | 580 | 30 | 0,06 |
| Pevnost betonu | fc | MPa | 20 | LN | 28 | 5 | 0,18 |
| Stálé zatížení | g | kNm−2 | 6,264 | N | 6,264 | 0,63 | 0,10 |
| Užitné zatížení | q | kNm−2 | 1,5 | GU | 0,9 | 0,315 | 0,35 |
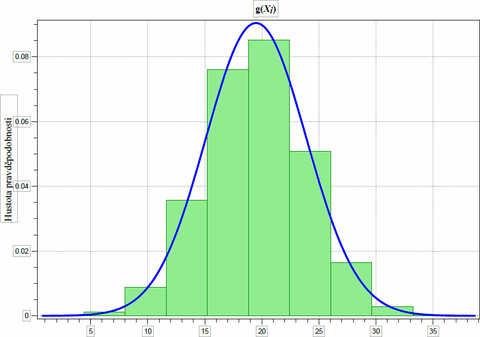
Uplatnění pravděpodobnostní metody pro stanovení pravděpodobnosti výskytu záporných hodnot funkce mezního stavu zpravidla vyžaduje aplikaci softwarových produktů (například jednoduchého softwaru COMREL [19] nebo VaP [20]). V případě hodnoceného stropního panelu vychází na základě modelů základních veličin uvedených v tab. 4 pravděpodobnost poruchy pf ≅ 10−5 a index spolehlivosti β ≅ 4,3 > 3,8. S ohledem na výsledek pravděpodobnostní metody je tedy konstrukce dostatečně spolehlivá. Hustot pravděpodobnosti (histogram) funkce mezního stavu je zachycena na obr. 1 (průměr 19,52 kNm, směrodatná odchylka 4,51 kNm).
Poznamenáme, že šikmost Gumbelova rozdělení je poměrně vysoká (1,14), což nemusí odpovídat skutečnému rozdělení užitného zatížení q. Alternativně lze předpokládat lognormální rozdělení, které může být výstižnější. Při použití Gumbelova rozdělení pro zatížení q je stanovená pravděpodobnost poruchy pf = 1 × 10−5 a index spolehlivosti β = 4,30. Tyto výsledky mohou být mírně konzervativní. Jestliže se předpokládá lognormální rozdělení s menší šikmostí (0,90), je výsledný index spolehlivosti β mírně vyšší (β = 4,35).
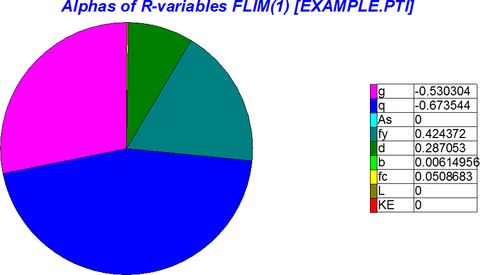
Vliv základních veličin na výslednou úroveň spolehlivosti je zachycen na obr. 2. Je zřejmé, že největší relativní vliv na výslednou úroveň spolehlivosti má užitné zatížení q (−67 %). Menší relativní vliv má stálé zatížení g (−53 %) a pevnost výztuže fy (42 %). Relativní vlivy základních veličin zachycených na obr. 2 také ukazují, že doporučené součinitel citlivosti veličin popisujících relativní vliv zatížení a odolnost αE = −0,7 a αR = 0,8 jsou značně konzervativním předpokladem.
5. Analýza rizik
Metody analýzy rizik mohou představovat účinný přístup k hodnocení důležitých staveb s nedostatečně únosnou konstrukcí, u kterých se operativní opatření zdají být nezbytná. V těchto případech může být přístup opírající se o analýzu rizik naznačený rovnicí (6.8) a detailně popsaný v mezinárodní normě ISO 2394 [3] nanejvýš užitečný. V případě menších konstrukcí (jako v hodnoceném stropním panelu), u kterých lze předpokládat operativní opatření (i když pouze pro zvýšení spolehlivosti), se mohou uplatnit metody optimalizace nákladů. Podrobnější popis optimalizačních postupů je uveden v dodatku 3 této přílohy.
6. Souhrn
Ukazuje se, že ověřování spolehlivosti stropního panelu metodou dílčích součinitelů vede k negativnímu výsledku, a to jak se součiniteli podle Eurokódů, tak s přizpůsobenými součiniteli (pro index spolehlivosti β = 3,8). Metoda stanovených hodnot (pro β = 3,8) poskytuje pozitivní výsledek. Pravděpodobnostní metoda poskytuje rovněž pozitivní výsledek s odhadnutou hodnotou indexu spolehlivosti β = 4,2, který je vyšší než požadovaná hodnota β = 3,8 pro zbývající životnost 50 let. Panel lze tedy považovat za dostatečně spolehlivý.
Přehled dílčích výsledků ověřování spolehlivosti stropního panelu jednotlivými metodami je uveden v tab. 5. Popsaný příklad ověřování spolehlivosti stropního panelu může poskytnout návod pro ověřování jednotlivých prvků existující konstrukce jako je nosník, sloup nebo mostní prvek. Je třeba zdůraznit, že je vždy nutné uvažovat skutečné podmínky působení konstrukce a dostupné informace o zatížení a odolnosti konstrukce. Jestliže jsou dostupné pouze omezené údaje, je možné využít statistické metody aktualizace informací. Ve všech případech je třeba zvážit požadovanou úroveň spolehlivosti (index β) a velikosti součinitelů citlivosti αE a αR. V některých důležitých případech je užitečné využít analýzy rizik. Jestliže se předpokládají případná konstrukční nebo provozní opatření, doporučuje se uplatnit metody optimalizace nákladů.
| Metoda | Účinek zatížení [kNm] | Odolnost [kNm] | Index β | Závěr |
|---|---|---|---|---|
| Dílčích součinitelů Eurokódů | 48,18 | 37,59 | Předpoklad 3,8 | Negativní |
| Přizpůsobených součinitelů | 41,87 | 39,75 | Předpoklad 3,8 | Negativní |
| Stanovených hodnot | 41,40 | 42,22 | Předpoklad 3,8 | Pozitivní |
| Pravděpodobnostní | – | – | Odhad 4,3 | Pozitivní |
Reference
- EN 1990 2002 Eurocode – Basis of structural design
- prEN 1990 2017 Eurocode – Basis of structural design
- JCSS 2001 Joint Committee for Structural Safety. “Probabilistic Model Code”, http://www.jcss.byg.dtu.dk/
- Holický M 2009 Reliability analysis for structural design, SUN MeDIA Stellenbosch, ZA, ISBN 978-1-920338-11-4, 199 pages
- Holický M. 2013 Introduction to Probability and Statistics for Engineers, Springer, Heidelberg, New York, London
- ISO 2394 2015 General Principles on Reliability for Structures
- COMREL version 6.00, Software product RCP, Consulting Software, Germany
- VaP Software product of PSP, Austria
Dodatek 1: Přizpůsobení dílčího součinitele pro odolnost
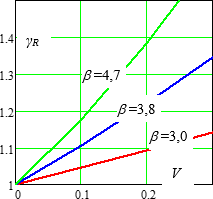
Obr. 3 Závislost dílčího součinitele γR (β,V) na koeficientu variability V pro vybrané hodnoty indexu spolehlivosti β = 3,0; 3,8 a 4,7
Dílčí součinitel γR pro odolnost R se stanoví za předpokladu lognormálního rozdělení na základě stanoveného indexu spolehlivosti β, variačního koeficientu V (zahrnujícího modelové nejistoty) a součinitele citlivosti αR ze vztahu
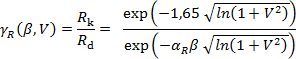
Za předpokladu součinitele citlivosti αR = 0,8 je závislost dílčího součinitele γR (β,V) na koeficientu variability V pro vybrané hodnoty indexu spolehlivosti β zachycena na obrázku 3.
Analogický postup platí pro přizpůsobení dílčích součinitelů stálého zatížení g a užitného zatížení q, pro které se případně využije jiné rozdělení.
Dodatek 2: Stanovená hodnota odolnosti
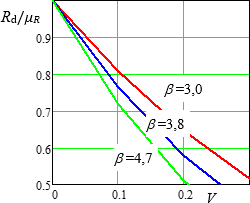
Obr. 4 Závislost poměru Rd(β,V) / μR na variačním koeficientu V pro vybrané indexy β = 3,0; 3,8 a 4,7
Stanovená hodnota Rd odolnosti R se určí za předpokladu lognormálního rozdělení na základě indexu spolehlivosti β, koeficientu variability V (včetně modelových nejistot) a součinitele citlivosti αR ze vztahu
Za předpokladu součinitele citlivosti αR = 0,8 je závislost poměru Rd(β,V) / μR na variačním koeficientu V pro vybrané indexy β zachycena na obrázku 4.
Analogický postup platí pro určení stanovených hodnot stálého zatížení g a užitného zatížení q, pro které se případně využije jiné rozdělení.
Dodatek 3: Optimalizace nákladů
Optimalizace nákladů muže být užitečná zejména pro jednotlivé konstrukční prvky, které mají přijatelnou úroveň spolehlivosti (jako v případě hodnoceného panelu), avšak uvažuje se o jejím zvýšení (konstrukčními a provozními opatřeními) během zbývající životnosti. V takovém případě se může uplatnit následující postup pravděpodobnostní optimalizace nákladů. Celkové náklady Ctot(x) včetně nákladů na zesílení konstrukce a provozní opatření mohou být vyjádřeny zjednodušeným vztahem (naznačeným v softwarovém produktu COMREL [19])
Veličina x = R/R0 reprezentuje parametr opatření, spotřebu materiálu a nezbytné náklady na zvýšení současné odolnosti R0 na požadovanou úroveň R. C0 představuje ostatní náklady opatření nezávislé na parametru x, C1 marginální náklady na jednotku parametru opatření x, Cf náklady vyvolané poruchou a vyloučením provozu konstrukce a pf (x) reprezentuje pravděpodobnost poruchy panelu. Přiložený obrázek 5 (vytvořený softwarovým produktem COMREL [19]) zachycuje závislost celkových nákladů Ctot(x) na parametru x pro vybrané hodnoty C0 = 0, C1 = 1, Cf = 100000 a panel s odolností x R0.
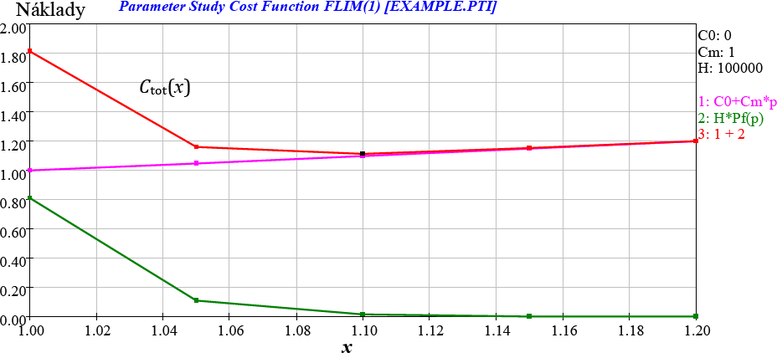
Obr. 5 Závislost celkových nákladů Ctot(x) na parametru x pro vybrané hodnoty C0 = 0, C1 = 1, Cf = 100000 a pravděpodobnost poruchy panelu pf(x) s odolností x R0
Minimální celkové náklady Ctot(x) předpokládané pro období zbývající životnosti 50 let odpovídají optimálnímu parametru x = R/R0 o přibližné hodnotě 1,10 a zvýšení odolnosti panelu o 10 %. Výsledné doporučení platí pouze pro hodnocený panel, vstupní data pro zatížení g, q, odolnost R a pro vybrané hodnoty relativních nákladů C0 = 0, C1 = 1, Cf = 100000. Pro korektní rozhodnutí o případných opatřeních by měl být kriticky uvážen vztah pro určení celkových nákladů Ctot(x) a všechny vstupní údaje o relativních nákladech.
An example of reliability verification of existing concrete member represent an extension of previous authors contribution “New European document for assessment of existing structures”. The illustrative example of the member is based on the new Technical specification [2]) and valid Eorocodes ČSN EN 1990 [7] and ČSN EN 1991-1-1 [9]. The contribution should provide background information supporting implementation of the new European document on assessment of existing structures to national standards.