Nelineární analýza železobetonového nosníku bez smykové výztuže na základě charakteristik betonu
© Fotolia.com
K analýze a dimenzování železobetonových konstrukcí je vyžadována znalost mechanických vlastností použitých materiálů. V případě nelineární analýzy je potřeba vyšší rozsah a podrobnost mechanických vlastností. Článek je zaměřen na ucelený popis pevnostních charakteristik betonu, pozornost se věnuje zejména pevnosti betonu v tahu. Testování se zaměřilo na zkoušku v příčném tahu a tří a čtyřbodovou zkoušku na ohyb. Získané mechanické vlastnosti betonu jsou následně uplatněny při nelineární analýze železobetonového nosníku s ohybovou výztuží, ale bez smykové výztuže, který byl podroben zatěžovací zkoušce.
Úvod
Stavební konstrukce musí splňovat řadu požadavků, mezi které patří kritéria spolehlivosti, bezpečnosti, hospodárnosti, použitelnosti a vzhledu. Ke stavebním materiálům, využívaným pro nosné konstrukce, patří často beton, který má nezastupitelný význam [1], [2]. Princip použití betonu je dobře známý. Nejsledovanější a nejdůležitější vlastností je jeho pevnost v tlaku, která je výrazně větší než pevnost betonu v tahu. Mechanické vlastnosti betonu ovlivňuje mnoho faktorů, z těchto důvodů je nutné brát v úvahu náhodný charakter materiálových vlastností [3], [4]. Pro potřeby návrhu železobetonových konstrukcí byla provedena klasifikace na třídy betonu, založené na pevnosti betonu v tlaku [5], [6]. V případě pokročilé analýzy zohledňující skutečné chování betonových konstrukcí [7], [8] je potřeba detailnější popis materiálových charakteristik. Stěžejní je pevnost betonu v tahu a parametry lomové mechaniky [9], [10], [11], [12]. Význam a rozšíření betonu je možné dokumentovat na řadě výzkumných úkolů a aktivitách oborových sdruženích FIB, RILEM zaměřující se na beton a betonové konstrukce na národní a světové úrovni. Optimalizací receptury, volbou výchozích surovin a technologií výroby vznikla celá řada variant betonu. Zastoupení běžných betonů v praxi má však významný podíl. S ohledem na hospodárnost a efektivitu návrhu je v některých případech vhodné přistoupit k nelineární analýze zohledňující skutečné chování konstrukčního prvku. Nelineární analýza skutečného chování je v některých případech vhodná také u již realizovaných konstrukcí při sanacích a rekonstrukcích. U těchto úloh je ale často problém s omezenou dostupností vstupních parametrů a vlastností betonu.
Výzkumná oblast a experimentální program
| Konzistence | S3 |
| Maximální zrno | 16 mm |
| Minimální obsah cementu | 300 kg |
| Vodní součinitel: v/c | 0,6 |
| Kamenivo 0/4 (těžené) | 870 kg |
| Kamenivo 4/8 (těžené) | 150 kg |
| Kamenivo 8/16 (těžené) | 820 kg |
| Voda | 189 l |
| Plastifikátor | 2,9 l |
Článek je zaměřen na popis mechanických vlastností betonu a to zejména pevnosti betonu v tahu u vybrané betonové směsi. Ucelený popis vlastností je následně využit k nelineární numerické analýze experimentu železobetonového nosníku s ohybovou výztuží, bez smykové výztuže. Složení betonové směsi je uvedeno v tab. 1. Maximální zrno betonové směsi bylo 16 mm a vodní součinitel 0,6. Pro beton se použil portlandský rychle tuhnoucí cement 42,5 MPa. Beton obsahuje také plastifikátor Stacheplast. Pro výrobu vzorků byl použit běžný beton pro konstrukční účely (např. základy, podlahy), viz obr. 1. Beton se vyráběl v betonárně v roce 2018 a byl přepravován jako transportbeton. Zkušební série zahrnovala více než 38 vzorků. Laboratorní zkoušky jsou doplněny zatěžovací zkouškou konstrukčního prvku – nosníku bez smykové výztuže. Pro nosník je stanovena únosnost dle platných norem a provedena numerická nelineární analýza chování prvku při zatěžování.
Zkušební program zahrnoval následující laboratorní zkoušky:
- Zkouška krychelné pevnosti v tlaku (150 mm × 150 mm × 150 mm),
- Zkouška válcové pevnosti v tlaku (150 mm × 300 mm),
- Zkouška pevnosti v příčném tahu (150 mm × 150 mm × 150 mm),
- Tříbodová zkouška na ohyb s vrubem 50 mm – 3B600 (průřez 150 mm × 150 mm),
- Tříbodová zkouška na ohyb s vrubem 25 mm – 3B500 (průřez 150 mm × 150 mm),
- Tříbodová zkouška na ohyb – 3B500 (průřez 150 mm × 150 mm),
- Čtyřbodová zkouška na ohyb – 4B600 (průřez 150 mm × 150 mm),
- Čtyřbodová zkouška na ohyb – 4B500 (průřez 150 mm × 150 mm).
Obr. 1 Zkušební vzorky jedné serie (po betonáži, před zkoušením)
Základní mechanické vlastnosti betonu
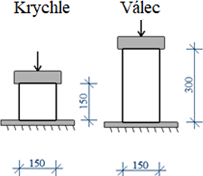
Obr. 2 Testování pevnosti v tlaku a modulu pružnosti
Základní mechanickou vlastností betonu je pevnost betonu v tlaku a modul pružnosti. Ke zkoušce pevnosti v tlaku se používají krychle o rozměrech 150×150×150 mm nebo válce o průměru 150 mm a výšky 300 mm. Válce se také využívají pro stanovení modulu pružnosti. Schéma zkoušky je patrné na obr. 2. Série zkušebních vzorků pro pevnost v tlaku obsahovala 6 krychlí a 3 válce. Výsledky měření jsou uvedeny v tab. 3.
Pevnost v tlaku na krychlích fc,cube se určí podle vzorce:
,
(1)
kde Pmax je maximální síla a a je velikost strany krychle.
V případě válcové pevnosti v tlaku fc se pevnost stanoví podle vzorce:
,
(2)
Zkoušení modulu pružnosti betonu je založeno na vyhodnocení rozdílu deformací pro různé intenzity zatížení. Postupy zkoušení modulu pružnosti v tlaku upravuje ČSN ISO 1920-10 [13]. Statický modul pružnosti se určí ze vztahu:
,
(3)
kde σa je horní zatěžovací napětí v N/mm2, σb je základní zatěžovací napětí v N/mm2 a Δε je průměrná změna poměrného přetvoření mezi horním a základním napětím. Výsledná změřená hodnota statického modulu pružnosti je výrazně menší, než hodnota, která je pro danou pevnost betonu uvedena v normě [1]. Rozdíl byl způsoben pravděpodobně vlivem použitého těženého kameniva, případně konzistencí a množstvím vody. Modul pružnosti však nebyl předepsán při objednávce jako závazné kritérium.
| Zkouška | Pevnost v tlaku – krychelná | Pevnost v tlaku – válcová | Modul pružnosti |
|---|---|---|---|
| Označení | fc,cube | fc | Ec |
| Jednotka | [MPa] | [MPa] | [GPa] |
| Průměr | 26,59 | 24,66 | 18,50 |
| Směr. odchylka | 1,88 | 0,58 | 0,50 |
| Vzorků | 6 | 6 | 3 |
Pevnost betonu v příčném tahu
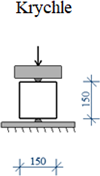
Obr. 3 Testování pevnosti v příčném tahu
Pro zkoušení pevnosti betonu v tahu je více metod. K nejrozšířenějším patří zkoušení pevnosti v příčném tahu. Využívá se standardních zkušebních těles ve tvaru krychle nebo válce. Konfigurace zkoušky je zobrazena na obr. 3. V rámci prezentovaného zkušebního programu se příčný tah stanovoval na vzorku tvaru krychle. Výchozí testování je v řezu kolmém na směr plnění, který je označován A. Pro ověření vlastností je zkoušen směr rovnoběžný se směrem plnění, který je označen B. Výsledná pevnost v příčném tahu se určí vztahem:
,
(4)
kde Pmax je maximální zatížení, l délka dotykové přímky tělesa a d je zvolený příčný rozměr tělesa. Výsledné vyhodnocení zkoušek v příčném tahu je uvedeno v tab. 4.
| Zkouška | Pevnost v příčném tahu – A |
|---|---|
| Označení | fc, sp, A |
| Jednotka | [MPa] |
| Průměr | 2,21 |
| Směr. odchylka | 0,27 |
| Vzorků | 6 |
Tříbodová zkouška na ohyb
Pro testování jsou zvoleny tři varianty zkoušek, schéma viz obr. 4. Zkouška označená 3B600 je pro trámec velikosti 150×150×700 mm, rozpětí 600 mm a průřez má zářez vysoký 50 mm. Druhá varianta označená 3B500 je pro trámec velikosti 150×150×600 mm a rozpětí 500 mm bez zářezu. Třetí varianta je označena 3B500_25 je pro trámec velikosti 150×150×600 mm, rozpětí 500 mm a má zářez vysoký 25 mm. Výsledky jsou uvedeny v tab. 5. Zkoušky se liší především místem lokalizace vzniku trhliny. U zkoušek s vrubem/zářezem je místo vzniku trhliny předem definováno. U zkoušky bez zářezu/vrubu se trhlina lokalizuje v nejslabším místě v blízkosti břemene/síly.
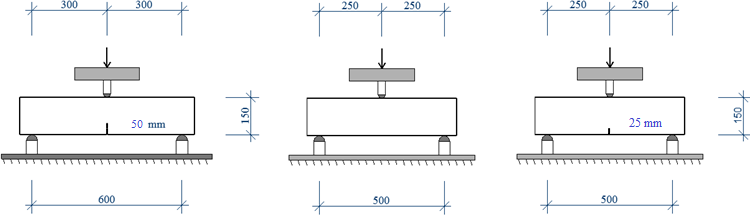
Obr. 4 Tříbodová ohybová zkouška
Vyhodnocení a výpočet pevnosti v tahu z tříbodové ohybové zkoušky je ovlivněn předpokládaným rozložením napětí po průřezu. Předpokládá se nelineární chování betonu, dochází k plastizaci a vznikají mikrotrhliny. Pevnost betonu v tahu pro tříbodovou zkoušku v ohybu se pak může vypočítat ze vztahu:
,
(5)
kde Pmax je maximální zatížení; L, b a h jsou rozměry: rozpětí, šířka a výška průřezu a a0 je výška zářezu.
| Označení | Pozice zatížení [mm] | Vrub a0 [mm] | Rozpětí L [mm] | Počet vzorků | fct,fl,3B [MPa] |
|---|---|---|---|---|---|
| 3B500 | 250/250 | – | 500 | 3 | 3,22 |
| 3B500_25 | 250/250 | 25 | 500 | 3 | 3,31 |
| 3B600 | 300/300 | 50 | 600 | 3 | 3,15 |
Rozdíly v pevnostech v tahu za ohybu, která se stanovila různými metodami, nejsou velké. S ohledem na počet vzorků lze zhodnotit, že materiálové vlastnosti vzorků jsou podobné, betonová směs homogenní a vliv zářezu a lokalizace porušení byl tedy malý.
Čtyřbodová zkouška na ohyb
Mezi další zkoušky pevnosti betonu v tahu patří čtyřbodový ohyb. Opět existují různé konfigurace, které se liší především rozpětím podpor a polohou zatížení. V rámci experimentálního programu byly provedeny dvě varianty 4B600 a 4B500, schéma zkoušky je na obr. 5. Zkouška označená 4B600 je pro trámec nominální velikosti 150×150×700 mm a rozpětí 600 mm. Vzdálenost mezi podporami a silami je 200 mm. Druhá varianta čtyřbodové zkoušky na ohyb je označená 4B500 a je určena pro trámec nominální velikosti 150×150×600 mm a rozpětí 500 mm. Zkouška se liší od předešlé umístěním sil. Vznik trhliny se lokalizuje u dolního povrhu trámce mezi silami. Souhrnně jsou výsledky uvedeny v tab. 6.
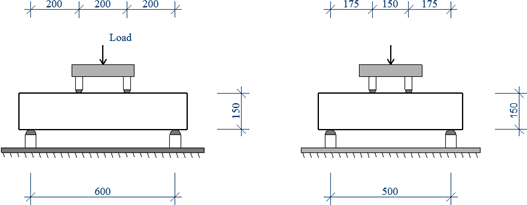
Obr. 5 Čtyřbodová ohybová zkouška
Pevnost v tahu za ohybu se může vyjádřit pro zkoušku 4B600, kde vzdálenost mezi podporami a břemeny je stejná, vztahem:
,
(6)
kde Pmax je maximální zatížení; L, b a h jsou rozměry: rozpětí, šířka a výška průřezu. V případě zkoušky 4B500 se vztah upravuje.
| Označení | Pozice zatížení [mm] | Rozpětí L [mm] | Vzorků | fct,fl,4B [MPa] |
|---|---|---|---|---|
| 4B600 | 200/200/200 | 600 | 2 | 3,08 |
| 4B500 | 150/175/150 | 500 | 3 | 3,54 |
Osová pevnost betonu v tahu
Přímé zkoušení pevnosti v jednoosém tahu je také možné, je ale významně ovlivněno okrajovými podmínkami, např. způsobem uchycení zkušebního tělesa a velikostí zkušebního tělesa. Provedený ucelený soubor zkoušek však umožnuje provést širší srovnání a pevnost v jednoosém tahu stanovit pomocí známých vztahů, které jsou ověřeny na velkém množství experimentů. Obvykle se používá vztah (7) pro přepočet pevnosti v příčném tahu a vztah (8) pro přepočet pevnosti v tahu za ohybu podle Model Code 2010 [6]:
,
(7)
kde αsp je v intervalu 0,83 až 1,00.
,
(8)
kde αfl je v intervalu 0,57–0,66.
U betonu nižších pevností je vhodné volit součinitele u dolní hranice. Konkrétně je zvoleno pro fct,sp součinitel 1,0 v souladu s doporučením v Model Code 2010 [6]. V případě součinitele fct,fl je vhodné pro dopočet koeficientu zohlednit výšku nosníku hb :
(9)
Výsledné tahové pevnosti jsou uvedeny v tab. 7 a znázorněny graficky na obr. 6.
| Typ zkoušky | Příčný tah A | 3B500 | 3B500 | 3B600 | 4B600 | 4B500 |
|---|---|---|---|---|---|---|
| Pevnost v tahu [MPa] | 2,21 | 2,09 | 2,14 | 1,95 | 2,09 | 2,38 |
![Obr. 6 Výsledná přepočtená pevnost betonu v tahu [MPa]](/docu/clanky/0182/018218o18.png)
Obr. 6 Výsledná přepočtená pevnost betonu v tahu [MPa]
Experiment – nosník
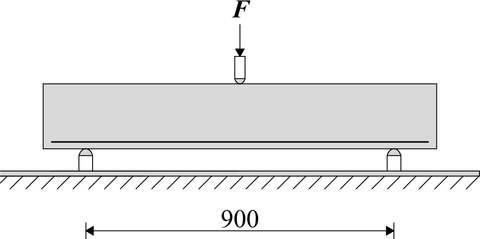
V rámci výzkumu se provedla zatěžovací zkouška tříbodovým ohybem malého konstrukčního prvku. Nosník obdélníkového průřezu o rozměrech 100 × 190 mm a délce 1 150 mm byl zatížen dle schématu na obr. 7. Nosník byl vyztužen dvěma pruty betonářské výztuže B500B o průměru 10 mm u spodního okraje, krytí výztuže bylo 20 mm. Jedná se o ocel bez výrazné meze kluzu, vycházelo se tedy ze smluvní meze kluzu 500 MPa, mez pevnosti se předpokládá 600 MPa. Záznam zatěžování byl získán ze zkušebního lisu a extenzometru. Svislý průhyb nosníku se měřil uprostřed rozpětí u dolního povrchu. Nosník se zatěžoval deformačním zatížením.
Z průběhu experimentu bylo zjištěno, že první mikrotrhliny vznikly u dolního okraje uprostřed rozpětí. Postupným dalším zatěžováním začala vznikat šikmá smyková trhlina, která postupně propagovala od dolního k hornímu okraji a následně vedla ke kolapsu nosníku. Maximální dosažené zatížení bylo 40,81 kN, porušený nosník je na obr. 10.
Únosnost v ohybu a ve smyku podle platné normy
Při zatěžovací zkoušce je trámový prvek namáhán ohybem a smykem. Při výpočtu únosnosti průřezu v ohybu podle platných norem [1], [2] se vychází z dvojice sil mezi tlačeným betonem a taženou výztuží v kritickém průřezu. Normový postup umožnuje více přístupů, kdy očekávaná momentová únosnost stanovená za předpokladu rovnoměrného rozdělení napětí v tlačené oblasti betonu podle vzorce (10) a (11) se stanoví:
,
(10)
kde výška tlačené oblasti x se určí podle vzorce (11):
,
(11)
kde bw je šířka průřezu, fc se uvažuje jako válcová pevnost betonu podle výsledků zkoušek, As je plocha výztuže, fs je pevnost výztuže, d efektivní výška průřezu, λ se uvažuje hodnotou 0,8. Teoretická hodnota momentu určená výztuží a účinnou výškou průřezu je 12,95 kNm, což odpovídá zatěžovací síle 57,56 kN podle obr. 7.
Obr. 7 Schéma zatěžovací zkoušky tříbodovým ohybem
Porušení smykem je složitý mechanismus, který je ovlivněn tvarem průřezu, polohou zatížení a způsobem vyztužení. Specifickým případem je analyzovaný nosník bez smykové výztuže. Podle platné normy pro navrhování [1], [2] se stanovuje smyková únosnost nosníku bez smykové výztuže a bez působící osové síly podle vzorce (12):
,
(12)
kde Cc se uvažuje hodnotou 0,18, k je parametr výšky průřezu, který byl stanoven hodnotou 2, fc se uvažuje jako průměrná válcová pevnost betonu, bw je šířka průřezu, d efektivní výška průřezu, ρl je stupeň vyztužení ohybovou výztuží v podélném směru, Vmin je minimální hodnota smykové únosnosti. Výsledná únosnost průřezu ve smyku bez smykové výztuže je 17,00 kN, což odpovídá silovému zatížení 34,00 kN dle schématu na obr. 7.
Nelineární analýza
Obr. 8 Schéma tříbodové zkoušky na ohyb
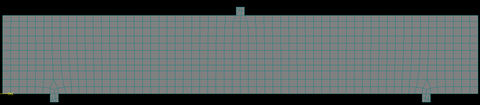
Ucelený soubor mechanických vlastností betonu je možné využít k nelineární numerické analýze tříbodové zatěžovací zkoušky nosníku. Nelineární analýza konstrukce je vhodná zejména ve složitých případech pro doplnění návrhových modelů uvedených v normách. Výpočet se provádí v postupných zatěžovacích krocích, předpokládá se nelineární chování betonu i oceli. V rámci numerického modelování bylo cílem určit celkovou únosnost nosníku a způsob porušení. K numerickému modelování se využilo 2D výpočetních modelů, konkrétně byl zvolen model betonu SBETA, který se využívá v systému ATENA [12]. 2D model zahrnuje betonový nosník, výztuž, ocelovou zatěžovací desku a podpory. Síť konečných prvků je tvořena generátorem. Při výpočtu se vycházelo z doporučení a modelů [8], [12]. Pro nelineární řešení úlohy byla použita metoda Newton-Raphson. Zatížení se vnášelo deformací. Vstupní materiálové charakteristiky betonu se použily z laboratorních zkoušek, pouze lomová energie se dopočetla dle doporučení manuálu ATENA. Výpočetní model je zobrazen na obr. 8.
Porovnání experimentu a numerické analýzy
Obr. 9 Výsledky zatěžovací tříbodové zkoušky a nelineární numerické analýzy
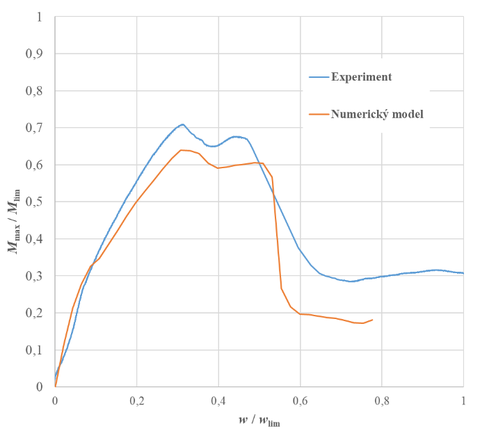
Vyhodnocení zatěžovací zkoušky a výsledek navazující nelineární analýzy jsou zobrazeny formou grafu na obr. 9. Je znázorněna závislost mezi ohybovým momentem a deformací vztaženou k momentu na mezi únosnosti a stanovenému limitnímu průhybu l/200 rozpětí. Z obou křivek grafu, které vykazují velkou míru shody, jsou patrné typické fáze zatěžovaní betonových prvků. Jedná se o oblast před vznikem trhlin, rozvoje trhlin a kolapsu nosníku. Kolaps nosníku nastal v důsledku smyku. Výpočetní model v nelineární analýze má na počátku větší tuhost než experiment. Výsledné dosažené maximální zatížení v numerickém modelu je 36,81 kN, liší se jen o 4 kN od maximálního zatížení při zatěžovací zkoušce. Stejný mechanismus rozvoje smykové trhliny v experimentu a numerickém modelu je patrný z obr. 10 a obr. 11.
Obr. 10 Nosník po zkoušce – smyková trhlina
Obr. 11 Numerická simulace – smyková trhlina (min. tl. 0,1 mm vykreslené trhliny)
Závěr
Článek se zabývá určením mechanických vlastností u vybrané betonové směsi, pro kterou se provádělo 10 různých typů zkoušek. Množství zkoušek a malý rozptyl výsledných hodnot měření prokazují homogenitu zkoušené betonové směsi. Byly provedeny zkoušky válcové a krychelné pevnosti a stanoven modul pružnosti. Bylo provedeno několik typů zkoušek tahové pevnosti. Výsledné průměrné hodnoty pevnosti betonu v tahu vypočtené na základě zkoušek jsou od 1,95 do 2,38 MPa. Lze doporučit použít více typů zkoušek pro stanovení pevnosti betonu v tahu, získané hodnoty tak ověřit a vypočítat průměrné výsledné hodnoty. Tyto je možné pak považovat jako vhodné vstupní parametry pro nelineární analýzu skutečného chování betonových konstrukcí.
Srovnáním záznamu zatěžovací zkoušky nosníku s výsledky numerického modelování je možné hodnotit vypočtenou analýzu jako velmi výstižnou, rozdíl je cca 10 procent. Povedlo se modelovat jak rozvoj smykových trhlin, tak skutečný kolaps konstrukce. Ucelený soubor laboratorních zkoušek tedy dostatečně popisuje mechanické vlastnosti betonu potřebné k nelineární analýze. Malý rozdíl je také mezi smykovou zatížitelností stanovenou dle platných norem a maximální dosaženou zatěžovací silou při experimentu. Nelineární analýza umožňuje stanovit únosnost průřezu zobecněným postupem a doplnit tak stanovení únosnosti dle platných norem.
Poděkování
Tento výsledek byl získán za finanční podpory projektu GAČR 16-08937S „Stav napětí a deformace vláknobetonových kompozitů v interakci se zemním prostředím“.
Reference
- Procházka, J., Štěpánek P., Krátký, J., Kohoutková, A., Vašková, J., Navrhování betonových konstrukcí 1, prvky z prostého a železového betonu, ČBS ČSSI, 2006.
- Bilčík J., Fillo L, Benko V., Halvonik J., Betónové konštrkcie, STU v Bratislavě 2008, ISBN 978-80-227- 2940-6.
- ISO 2394: Obecné zásady spolehlivosti konstrukcí. (General Principles on Reliability for Structures).
- ISO. JCSS (2016), Probabilistic Model Code, JCSS Working Material, http://www.jcss.byg.dtu.dk.
- CEB-FIP MODEL CODE 1990: DESIGN CODE, (Final version published by Thomas Telford Ltd., London), 1993
- Model Code 2010 – Final Draft, fib, Bulletin No 65 and 66. 1-2. 2012.
- RILEM (2011): About Rilem [Online], url: https://www.rilem.net [Accessed on 4 May 2011].
- Sucharda, O., Konecny, P. Recommendation for the modelling of 3D non-linear analysis of RC beam tests, Computers and Concrete, 21 (1), pp. 11–20, 2018. DOI:10.12989/cac.2018.21.1.011
- Bazant, Z. and Planas, J. (1998), Fracture and Size Effect in Concrete and Other Quasibrittle Materials, CRC Press Boca Raton, FL.
- Strauss, A., Zimmermann, T., Lehký, D., Novák, D. and Keršner, Z. (2014), Stochastic fracture-mechanical parameters for the performance-based design of concrete structures, Struct. Concrete, 15(3), 380–394.
- Karihaloo B. Fracture Mechanics of Concrete. Longman Scientific & Technical, New York (1995).
- Cervenka, V., Jendele, L., Cervenka J. ATENA Program documentation – Part 1: Theory. Cervenka Consulting. Pratur. 2016.
- ČSN ISO 1920-10: Zkoušení betonu – Část 10: Stanovení statického modulu pružnosti v tlaku.
Analysis and design of reinforced concrete structures requires knowledge of the mechanical properties of the materials used. In the case of nonlinear analysis, a higher range and detail of mechanical properties of concrete is needed. The article focuses on the description of strength characteristics of concrete, attention is paid to the strength of concrete in the tension. The testing was focused on the split tension test and the three-point and four-point bending test. The obtained mechanical properties of concrete are subsequently applied in the nonlinear analysis of reinforced concrete beam without shear reinforcement, which has been subjected to a load test.