Reklama

Kontaktní zateplení z pohledu Tepelných mostů hmoždinkami a jejich prokreslování

27.2.2012

Ing. Roman Šubrt, sdružení Energy Consulting České Budějovice, Ing. Pavlína Charvátová, VŠTE České Budějovice

Recenzovaný

V zásadě lze provádět tři druhy zateplování. Kontaktní zatepelní z exteriéru, odvětrávané zateplení z exteriéru a zateplení z interiéru. Každé toto řešení má svoje výhody i nevýhody. Jako nejlevnější a nejméně problematické řešení pro většinu domů se jeví vnější kontaktní zateplovací systém (ETICS). Ten je složený z lepidla, dále tepelného izolantu, nejčastěji v ČR minerální vlny či pěnového polystyrenu. Tyto tepelné izolanty jsou pak obvykle dále kotveny hmoždinkami a přes ně je provedena vrstva lepidla s výztužnou tkaninou a finální omítka. U tohto systému se v poslední době ukazují jako problematická místa kotvící hmoždinky, a to hned ze dvou příčin.

Reklama

Ustálený teplotní stav – kvantifikace bodových tepelných mostů hmoždinkami

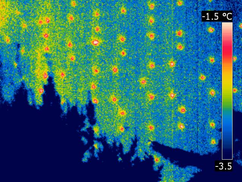
Tepelné mosty lze rozdělit na tepelné vazby vznikající napojením dvou konstrukcí a tepelné mosty v konstrukci, které jsou nahodilé či systematické. Podrobněji se tepelným mostům věnujeme na našem webu www.tepelnymost.cz. K systematickým tepelným mostům patří i každá hmoždinka procházející skrz tepelný izolant. Význam tohoto tepelného mostu stoupá ze třech důvodů. Prvním je, že vlivem změny normy na zatížení větrem je nutné navrhovat větší počty hmoždinek, a tak se ty tepelné mosty, které mohly být zanedbávány pro svůj malý rozsah, mohou ukázat jako významné. To je dokumentováno na obr. 1 a termogramu 1, kde je štítová stěna panelového domu, příp. na obr. 2 a termogramu 2, kde je průčelí panelového domu. Druhým důvodem je, že se používají větší tloušťky tepelných izolantů, a tudíž se používají pro kotvení hmoždinky s kovovým rozpěrným prvkem (trn, vrut), které jsou pochopitelně větším tepelným mostem. Třetím důvodem pak je, že bodové tepelné mosty hmoždinkami jsou minimálně závislé na tloušťce tepelného izolantu, a tak tam, kde u slabších tepelných izolantů tvořily tepelné mosty hmoždinkami procentuálně malé zhoršení tepelně izolačních vlastností, u větších tlouštěk tepelného izolantu je toto procento výrazně větší.

Při kvantifikaci tepelného mostu hmoždinkou je možné vycházet z jejich zatřídění a nebo vycházet z přesnějších výpočtů.

Intenzita tepelného toku v místě tepelného mostu je potom dána nejen typem hmoždinky a tloušťkou tepelného izolantu (i když, jak již bylo řešeno, tento vliv je minimální), ale také hloubkou ukotvení do podkladu a samozřejmě i konstrukcí, do které je hmoždinka kotvena.

Obr. 2 – průčelí panelového domu

Termogram 2

Obr. 1 – štítová stěna panelového domu

Termogram 1

V tabulce 1 jsou uvedeny hodnoty bodového činitele prostupu pro několik druhů hmoždinek, tlouštěk tepelného izolantu a dvou druhů konstrukce. Při kvantifikaci tepelného mostu hmoždinkami byly zvoleny hmoždinky EJOT NT U, což je zatloukací hmoždinka s kovovým trnem a náliskem umělé hmoty pro přerušení tepelného mostu – viz. obr. 3 a dále EJOT NTR U, což je šroubovací hmoždinka, kterou lze alternativně překrýt zátkou z tepelné izolace – viz. obr. 4. Tloušťky tepelného izolantu byly voleny od 100 do 160 mm po 20 mm a v některých případech byly zvoleny i tloušťky 60, 80 a 95 mm tak, aby došlo k potvrzení předpokladu, že tloušťka tepelného izolantu má na hodnotu bodového činitele prostupu tepla minimální vliv. Za zateplované kosntrukce byl zvolen v první fázi železobeton tl. 140 mm. Tento materiál patří ve stavebnictví k velmi tepelně vodivým materiálům. Jeho použití způsobí největší tepelné mosty hmoždinkou, neboť jím bude teplo intenzivně přiváděno k hmoždince. Jako druhý materiál zdiva byla zvolena klasická cihelná zeď tloušťky 45 cm. Tato volba byla učiněna proto, že se jedná o nejrozšířenější běžné zdivo. Aby byla simulována realita, byly mimo použití hmoždinky NT U a STR U bez zátky z tepelného izolantu a se zátkou z tepelného izolantu simulovány i hmoždinky STR U zapuštěné 5 mm, popř. 10 mm do tepelného izolantu a vzniklá prohlubeň byla vyplněna fasádním lepidlem.

Obr. 3 – hmoždinka EJOT NT U

Obr. 4 – hmoždinka EJOT NTR U

Výkresy jednotlivých hmoždinek jsou patrné z obr. 5. Výsledné hodnoty bodového činitele prostupu tepla jsou v tabulce 1.

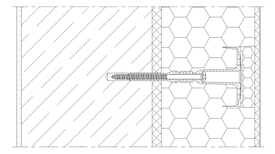
Obr. 5a – hmoždinka STR U s překrytím zátkou z pěnového polystyrénu

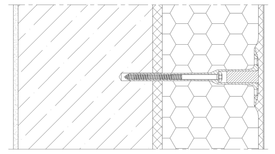
Obr. 5b – hmoždinka STR U bez zapuštění

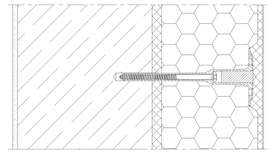
Obr. 5c – hmoždinka STR U se zapuštěním 5 mm a překrytím lepidlem

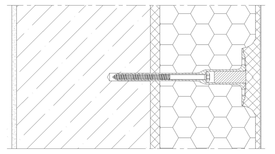
Obr. 5d – hmoždinka STR U se zapuštěním 10 mm a překrytím lepidlem

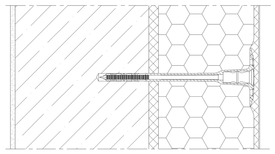
Obr. 5e – hmoždinka NT U bez zapuštění

Tabulka 1 – hodnoty bodového činitele prostupu tepla
Typ hmoždinky	Tloušťka tepelného izolantu [mm]	Bodový činitel prostupu tepla [W/K]
Typ hmoždinky	Tloušťka tepelného izolantu [mm]	železobeton tl. 140 mm	zdivo cihelné z cihel plných tl. 450 mm
STRU se zátkou z EPS	100	0,00056	0,00054
STRU se zátkou z EPS	120	0,00079	0,00058
STRU se zátkou z EPS	140	0,00082	0,00065
STRU se zátkou z EPS	160	0,00082	0,00067
STRU nezapuštená	60	0,00114	0,00072
STRU nezapuštená	80	0,00119	0,00083
STRU nezapuštená	95	0,00119	0,00087
STRU nezapuštená	100	0,00117	0,00088
STRU nezapuštená	120	0,00082	0,00074
STRU nezapuštená	140	0,00083	0,00076
STRU nezapuštená	160	0,00083	0,00077
STRU zapuštená 5 mm	60	0,00131	0,00083
STRU zapuštená 5 mm	80	0,00128	0,00089
STRU zapuštená 5 mm	95	0,00125	0,00092
STRU zapuštená 5 mm	100	0,00125	0,00092
STRU zapuštená 5 mm	120	0,00101	0,00077
STRU zapuštená 5 mm	140	0,00099	0,00078
STRU zapuštená 5 mm	160	0,00096	0,00078
STRU zapuštená 10 mm	100	0,00133	0,00100
STRU zapuštená 10 mm	120	0,00107	0,00082
STRU zapuštená 10 mm	140	0,00104	0,00082
STRU zapuštená 10 mm	160	0,00099	0,00081
STRU zapuštená 15 mm	100	0,00147	0,00109
STRU zapuštená 15 mm	120	0,00116	0,00089
STRU zapuštená 15 mm	140	0,00110	0,00087
STRU zapuštená 15 mm	160	0,00104	0,00085
NTU nezapuštená	100	0,00133	0,00099
NTU nezapuštená	120	0,00126	0,00096
NTU nezapuštená	140	0,00118	0,00093
NTU nezapuštená	160	0,00111	0,00089

Uvedené bodové tepelné mosty jsou zdánlivě minimální, neboť se pohybují okolo 1 mW. Je však nutné si uvědomit, že výpočet byl prováděn s použitím kvalitních hmoždinek, kdy u hmoždinky NT nejde poškodit úderem kladiva nalisované plastové přerušení tepelného mostu a u hmoždinky NTR U nemůže nejen dojít k poškození přerušení tepelného mostu, které je řešeno zapuštěním šroubu do těla hmoždinky, ale nemůže dojít úderem kladiva ani k oddělení talíře hmoždinky od dříku, neboť se kladivo při montáži nepoužívá. Další skutečností je, že tepelné mosty jsou sice malé, ale jejich počet může být na větších domech významný. V tabulce 2 je uvedené zvýšení součinitele prostupu tepla pro stěnu z železobetonu v závislosti na počtu hmoždinek 1 m² konstrukce a tloušťce tepelného izolantu pro různé hmoždinky. Je patrné, že hmoždinka se zátkou z tepelné izolace má nejnižší vliv v na součinitel prostupu tepla U. Z tabulky je také patrné, že pro zkoumané hmoždinky a zkoumané tloušťky tepelných izolantů je vliv tepelných mostů v závislosti dle počtu hmoždinek na 1 m² až 0,01 W/(m².K). Pro méně kvalitní hmoždinky může být tento rozdíl větší.

Tabulka 2 – zvýšení součinitele prostupu tepla pro stěnu ze železobetonu v závislosti na počtu hmoždinek na 1 m² konstrukce a tloušťce tepelného izolantu pro různé hmoždinky
Typ hmoždinky	Tloušťka tepelného izolantu [mm]	Souč. prostupu tepla konstrukce bez hmoždinek `U` [W/(m².K)]	Souč. prostupu tepla konstrukce vč. hmoždinek `U` [W/(m².K)]					Procentuální zvýšení součinitele prostupu tepla `U` [%]
			počet hmoždinek na 1 m² konstrukce					počet hmoždinek na 1 m² konstrukce
			4	6	8	10	12	4	6	8	10	12
STRU se zátkou z EPS	100	0,348	0,351	0,352	0,353	0,354	0,355	0,62	0,93	1,24	1,55	1,86
STRU se zátkou z EPS	120	0,304	0,307	0,308	0,309	0,310	0,311	0,76	1,14	1,52	1,91	2,29
STRU se zátkou z EPS	140	0,264	0,267	0,268	0,269	0,271	0,272	0,98	1,48	1,97	2,46	2,95
STRU se zátkou z EPS	160	0,233	0,236	0,237	0,239	0,240	0,241	1,15	1,72	2,30	2,87	3,45
STRU nezapuštená	100	0,348	0,352	0,354	0,355	0,357	0,359	1,01	1,52	2,02	2,53	3,03
STRU nezapuštená	120	0,304	0,307	0,309	0,310	0,312	0,313	0,97	1,46	1,94	2,43	2,92
STRU nezapuštená	140	0,264	0,267	0,269	0,270	0,272	0,273	1,15	1,73	2,30	2,88	3,45
STRU nezapuštená	160	0,233	0,236	0,238	0,240	0,241	0,243	1,32	1,98	2,64	3,30	3,96
STRU zapuštená 5 mm	100	0,348	0,352	0,354	0,356	0,358	0,359	1,06	1,58	2,11	2,64	3,17
STRU zapuštená 5 mm	120	0,304	0,307	0,309	0,311	0,312	0,314	1,01	1,52	2,02	2,53	3,04
STRU zapuštená 5 mm	140	0,264	0,267	0,269	0,270	0,272	0,274	1,18	1,77	2,36	2,95	3,54
STRU zapuštená 5 mm	160	0,233	0,236	0,238	0,240	0,241	0,243	1,34	2,01	2,67	3,34	4,01
STRU zapuštená 10 mm	100	0,348	0,352	0,354	0,356	0,358	0,360	1,15	1,72	2,30	2,87	3,44
STRU zapuštená 10 mm	120	0,304	0,308	0,309	0,311	0,313	0,314	1,08	1,62	2,16	2,69	3,23
STRU zapuštená 10 mm	140	0,264	0,267	0,269	0,271	0,272	0,274	1,24	1,86	2,48	3,10	3,72
STRU zapuštená 10 mm	160	0,233	0,237	0,238	0,240	0,241	0,243	1,39	2,08	2,78	3,47	4,17
STRU zapuštená 15 mm	100	0,348	0,353	0,355	0,357	0,359	0,361	1,25	1,88	2,50	3,13	3,75
STRU zapuštená 15 mm	120	0,304	0,308	0,310	0,312	0,313	0,315	1,17	1,75	2,34	2,92	3,51
STRU zapuštená 15 mm	140	0,264	0,268	0,269	0,271	0,273	0,275	1,32	1,98	2,63	3,29	3,95
STRU zapuštená 15 mm	160	0,233	0,237	0,238	0,240	0,242	0,244	1,46	2,19	2,91	3,64	4,37
NTU nezapuštená	100	0,348	0,352	0,354	0,356	0,358	0,360	1,14	1,71	2,27	2,84	3,41
NTU nezapuštená	120	0,304	0,308	0,310	0,312	0,314	0,316	1,26	1,89	2,52	3,15	3,78
NTU nezapuštená	140	0,264	0,268	0,270	0,272	0,273	0,275	1,41	2,11	2,82	3,52	4,22
NTU nezapuštená	160	0,233	0,237	0,239	0,240	0,242	0,244	1,53	2,29	3,05	3,81	4,58

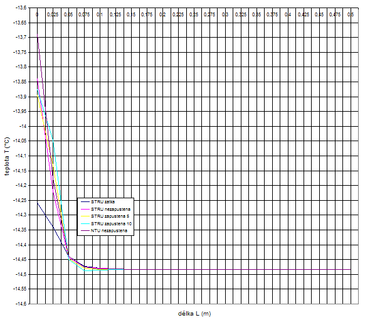
Graf 1

Na grafu 1 je uveden průběh teplot na povrchu fasády, přičemž jako počátkek je uveden střed hmoždinky. Ačkoliv je poloměr talíře hmoždinky 30 mm, je patrný vliv hmoždinky ještě více než 100 mm od jejího středu, tedy 70 mm za okrajem talíře hmoždinky.

Na závěr je nutné podotknout, že pokud je prováděna kvantifikace vlivu tepelného mostu hmoždinkami dle zatřídění, je nutné si uvědomit, že toto zatřídění obvykle vychází z předpisově zabudované hmoždinky, což velmi často není splněno. Hmoždinky bývají více zapuštěné do tepelného izolantu a přestěrkovány lepidlem. To pak tvoří nejen větší tepelný most, ale zároveň větší roznášecí plochu pro přechod tepla do exteriéru.

Neustálený teplotní stav – ozřejmění prokreslování hmoždinek na povrch fasády a způsob jeho zabránění

Obr. 7 – rozdílná kondenzace vodní páry na hmoždince a mimo ni

Obr. 6 – zaplísnění v místě hmoždinky

Druhou příčinou, proč jsou hmoždinky problematickým místem, je jejich tzv. prokreslování (hovorově nazýváno jako Dalmatinový efekt), tedy stav, kdy se za určitých tepelně vlhkostních předpokladů prokreslí na fasádu místo jejich ukotvení. To je zpočátku pouze dočasné, ale později se může stát i trvalým, neboť v místě kondenzace může docházet k intenzivnějšímu růstu plísní či se zde může zachytávat prach. Na obr. 6 je v pravé horní části vidět zaplísnění v místě hmoždinky. Obr. 7 dokumentuje rozdílnou kondenzaci vodní páry na hmoždince a mimo ni.

Správně zabudovaná hmoždinka je mírně vmáčknutá do tepelného izolantu tak, aby talíř hmoždinky lícoval s tepelným izolantem. I toto osazení způsobuje, že v místě hmoždinky je pod omítkou hmota o větší tepelně akumulační schopnosti než v okolí. Při realizaci kotvení hmoždinkami velmi často dochází k tomu, že hmoždinka není přesně zalícovaná s tepelným izolantem, ale je zapuštěná mírně pod povrch a zbývající část je pak přestěrkována lepidlem. Zde je důsledkem větší tepelný most i větší tepelně akumulační schopnosti v místě hmoždinky. Vzrůst tepelného mostu dokumentují tabulky 1 a 2. Při teplotních simulacích jsme se zabývali i vlivem tepelné akumulace na průběh teplot. Jako vzorová konstrukce byla zvolena stěna o skladbě: vnitřní omítka tl. 5 mm, železobeton tl. 140 mm, lepidlo tl. 10 mm, EPS tl. 100 mm, lepidlo tl. 5 mm a omítka tl. 1 mm. Výpočet byl prováděn na hmoždinkách STR U pro normální osazení, pro zapuštění a překrytí lepidlem v tl. 5 a 10 mm a s překrytím zátkou z pěnového polystyrénu. Dále byla uvažována hmoždinka NT U bez zapuštění.

Nestacionární teplotní stav více odpovídá realitě. Tyto cyklické jevy jsou v reálu velmi nepravidelné, a proto jsme ve výpočtu simulovali okamžitý pokles teploty exteriéru z hodnoty 0 °C na −15 °C, přitom počáteční stav při θ_e = 0 °C byl stacionární a taktéž konečný stav při θ_e = −15 °C byl stacionární. Zvolená hodnota okamžitého poklesu teploty exteriéru o 15 °C vychází ze zdokumentovaného poklesu teploty o tuto hodnotu během 5 minut [3].

Jak vyplývá z podstaty věci, lze obrátit znaménka + a − a výsledek bude stejný, pouze s obráceným průběhem. Krok výpočtu byl zvolen 30 sec., neboť postupnou iterací bylo zjištěno, že takto získané výsledky jsou již dostatečně přesné a přitom lze v reálném čase provést výpočet s dostatečně dlouhým časovým úsekem. Délka časového úseku, po který byl výpočet prováděn byl zvolen tak, aby na konci doby došlo k ustálenému teplotnímu stavu. Postupnou aproximací byla doba výpočtu zvolena na 2 hodiny. Ve výpočtech jsme sledovali rychlost chladnutí vnějšího povrchu konstrukce. Zvolili jsme několik bodů, které mají dostatečnou vypovídací hodnotu, konkrétně:

v ose hmoždinky
10 mm od osy hmoždinky
25 mm od osy hmoždinky
30 mm od osy hmoždinky
100 mm od osy hmoždinky
250 mm od osy hmoždinky

Postupné chladnutí v těchto bodech je patrné na grafech, kde:

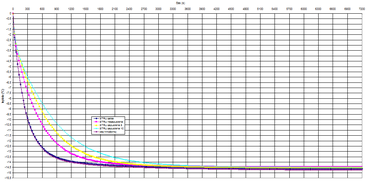
Graf 2 představuje pokles teploty povrchu zateplovacího systému ve středu hmoždinky při okamžitém poklesu teploty prostředí o 15 °C.

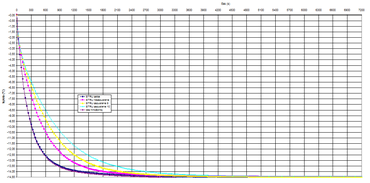
Graf 3 představuje pokles teploty povrchu zateplovacího systému 10 mm od středu hmoždinky při okamžitém poklesu teploty prostředí o 15 °C.

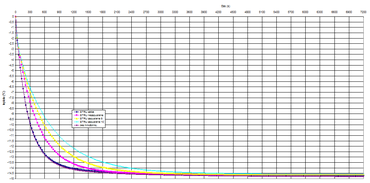
Graf 4 představuje pokles teploty povrchu zateplovacího systému 25 mm od středu hmoždinky při okamžitém poklesu teploty prostředí o 15 °C.

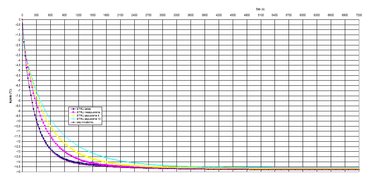
Graf 5 představuje pokles teploty povrchu zateplovacího systému 30 mm od středu hmoždinky při okamžitém poklesu teploty prostředí o 15 °C.

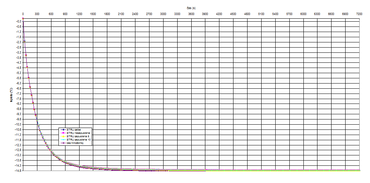
Graf 6 představuje pokles teploty povrchu zateplovacího systému 100 mm od středu hmoždinky při okamžitém poklesu teploty prostředí o 15 °C.

Největší teplotní rozdíl mezi chladnoucím povrchem fasády uprostřed hmoždinky a mimo hmoždinku byl tam, kde byla hmota o největší akumulační schopnosti, tedy u hmoždinky STR U se zapuštěním 10 mm a následným překrytím lepidlem. Největší rozdíly teploty a časy, kdy k těmto rozdílům došlo jsou patrné z tabulky 3.

Tabulka 3 – rozdíl povrchových teplot v místě středu hmoždinky a mimo ni v závislosti na čase při okamžitém poklesu teploty exteriéru o 15 °C
Hmoždinka	Max. rozdíl povrchových teplot u zateplovacího systému [°C]	Čas, ve kterém k tomuto rozdílu došlo [sec]
STR-U + zátka	0,1001	270
STR-U nezapuštěná	2,71165	330
STR-U zapuštěná 5 mm	3,83573	390
STR-U zapuštěná 10 mm	4,4349	420

Pokud bychom se soustředili na okraj talíře hmoždinky, tedy na vzdálenost 30 mm od středu hmoždinky, byly by rozdíly povrchových teplot v tomto místě a v místě zateplovacího systému bez hmoždinky již nižší, i tak se však jedná o dost značné hodnoty. Toto je uvedeno v tabulce 4.

Tabulka 4 – rozdíl povrchových teplot v místě okraje talíře hmoždinky a mimo ni v závislosti na čase při okamžitém poklesu teploty exteriéru o 15 °C
Hmoždinka	Rozdíl povrchových teplot u zateplovacího systému v místě okraje hmoždinky a na zateplovacím systému bez hmoždinky [°C]	Čas, ve kterém k tomuto rozdílu došlo [sec]
STR-U + zátka	0,1001	270
STR-U nezapuštěná	1,72785	330
STR-U zapuštěná 5 mm	2,62532	390
STR-U zapuštěná 10 mm	3,19052	450

Porovnáním tabulek 3 a 4 zjistíme, že směrem od středu hmoždinky k jejímu okraji se zmenšuje vliv tepelné akumulace hmoždinky a lepidla, což je logické, avšak toto zmenšení rozdílů není příliš výrazné.

Z obou tabulek pak vyplývá, že překrytí talíře hmoždinky tepelným izolantem způsobuje, že vliv hmoždinky na rozdílnou povrchovou teplotu vyvolanou změnou teploty exteriéru prakticky není žádný, a tudíž překrývání hmoždinek vede k zabránění tzv. dalmatinového efektu, jehož princip vzniku byl popsán výše.

Veškeré výpočty byly provedeny programem QuickField 5.7 v souřadnicovém systému r, z. Pro výpočet bodového činitele prostupu tepla byl proveden výpočet v programu pro konstrukci o stejných rozměrech jako výpočet s vloženou hmoždinkou, ovšem při zadání skladby bez hmoždinky. Tento postup byl zvolen proto, že při výpočtu může vlivem drobných nepřesností v numerickém modelu dojít k mírně rozdílným tepelným tokům, což by mohlo ovlivnit přesné stanovení bodového činitele prostupu tepla χ [W/K].

Poznámka pro fyziky a matematiky na závěr

Při interpretaci těchto tepelně technických výpočtů je potřeba si uvědomit, že se jedná o jisté zjednodušení, které je dáno principem výpočtu a zároveň, že výpočty mohou být provedeny pouze s jistou přesností vycházející z výpočtových postupů (metoda konečných prvků). V textu a v tabulkách jsou výsledky záměrně nezaokrouhlené proto, aby bylo patrné, jak se jednotlivé výpočty liší a tudíž bylo možné odhadnout přesnost výpočtu. Vliv tepelného mostu se počítá tak, že se vypočítá tepelný tok v jednorozměrném vedení tepla při zanedbání geometrie, která tepelný most způsobuje (v tomto případě hmoždinka a nepravidelnost jí způsobená) a tepelný tok ve dvourozměrném vedení tepla, přitom musí být zachována stejná geometrie řešeného detailu. Rozdíl těchto tepelných toků je pak vliv tepelného mostu. Z uvedeného principu vyplývá, že při minimálním vlivu tepelného mostu se od sebe odečítají téměř stejně velké hodnoty tepelných toků, jejichž výpočet je však již ovlivněn použitým matematickým modelem. Z tohoto důvodu je nutné brát vypočtené a zde uvedené hodnoty lineárních činitelů prostupu tepla jako ne zcela přesné a je nutné uvažovat s určitou možnou odchylkou mezi vypočtenými hodnotami a hodnotami skutečnými. Ve stavební praxi jsou však tyto rozdíly opominutelné, neboť do výpočtů je zanešeno významně větší množství nepřesností, které větší mírou ovlivní rozdíl mezi skutečností a výpočtovým modelem. Této nepřesnosti by šlo zamezit zaokrouhlováním, v tomto případě na desetitisíciny W/(m.K), což je druhá platná číslice. (Součinitel tepelné vodivosti se dle normy ČSN 73 0540-2 zaokrouhluje při U_N ≤ 0,4 W/(m²‧K) na setiny, tedy na druhou platnou číslici.)

Výpočty byly původně prováděny pro běžné tloušťky dnes používaných zateplovacích systémů, tedy v rozmezí 100 až 160 mm. Vzhledem k tomu, že nás kvantifikaci tepelných mostů nepravidelnost výsledků překvapila, byly pro ověření provedeny v některých případech i výpočty na tloušťky tepelných izolantů neprováděných, a to na tl. tepelného izolantu 60 mm, 80 mm a 95 mm. Zejména poslední rozměr je zcela mimo jakýkoliv výrobní rozměr tepelného izolantu, tato tloušťka však byla zvolena tak, aby byla blízko hodnotě tloušťky tepelného izolantu 100 mm.

Uvedené výpčty sledují možnost teplotních anomálií na zateplovacím systému vlivem akumulace tepla v konstrukci. Další možnou příčinou nestejnorodé kondenzace na povrchu zateplovacího systému může být vliv výměny tepelné energie sáláním s otevřenou oblohou (teplota vesmíru je cca 2 K, tj. −271 °C), kde na množství energie má vliv 4. mocnina absolutní teploty, tedy od 0 K, tj. −273,15 °C. Pokud z tohoto důvodu vznikne na povrchu zateplovacího systému námraza, může v místě hmoždinky dojít k jejímu roztání vlivem dotace tepla tepelným mostem tvořeným hmoždinkou.

Literatura

[1] Výpočtový prgram Quickfield 5.7, Tera Analysis Ltd., 2010
[2] Šubrt, R.: Některé tepelné mosty a jejich praktický význam na tepelné ztráty, in: Zborník prednášok TOB, 2005
[3] Pašek, J.: Analýza nesilových namáhání kontaktních zateplovacích systémů za použití infračervené termografie. Poruchy a rekonstrukce 2007 – Stavební fyzika v pozemním stavitelství. VŠB-TU Ostrava, 2007, Ostrava. ISBN 978-80-248-1404-9

Upraveno dle recenzenta

English Synopsis

ETICS in terms of heat bridges by plugs

As the cheapest and least problematic solution of thermal insulation for most buildings is the external thermal insulation composite system (ETICS). It is composed of the adhesive, as well as thermal insulation, mostly in the CR mineral wool or expanded or extruded polystyrene. These types of thermal insulation are usually anchored by plugs and all these parts are covered by the adhesive layer with reinforced fabric and the final render. For this system has recently been shown that the points of the plugs are problematic.