Vliv kondenzace vodní páry na účinnost výměníku pro zpětné získávání tepla
Kondenzace vodní páry není v běžných výměnících pro zpětné získávání tepla výjimečným stavem, ovšem její vliv se obvykle zanedbává. V článku je popsáno, jak může navýšení tepelného toku sdíleného mezi ochlazovaným a ohřívaným vzduchem o vázané teplo při kondenzaci vodní páry obsažené ve vzduchu teoreticky ovlivnit účinnost výměníku.
Úvod
V moderních vzduchotechnických jednotkách je dnes výměník pro zpětné získávání tepla (dále ZZT) naprostou samozřejmostí. Jeho funkcí je zajistit využití co největší části tepla obsaženého v odpadním vzduchu pro předehřev čerstvého venkovního vzduchu. Výměník ZZT není výhradní doménou staveb navržených s cílem co nejnižší spotřeby tepla a výjimečně se dnes při návrhu větracího systému diskutuje, jestli zpětné získávání tepla z odpadního vzduchu použít či ne. Jeho přínos pro energetickou bilanci celého větracího systému byl popsán na stránkách tohoto časopisu (VVI), v mnoha publikacích [1], [2], aj. Tento článek má za cíl zaměřit se na provozní stav, který není obvykle pro vyhodnocení přínosu uvažován. Během přechodného a zimního období dochází na teplosměnné ploše běžného deskového výměníku ZZT ke kondenzaci vodní páry z odpadního vzduchu. Tím se z proudu vzduchu do desky sdílí i skupenské teplo a celkový tepelný tok z ochlazovaného (odpadního) do ohřívaného (čerstvého) vzduchu se tím zvyšuje. Předmětem tohoto článku je posouzení, jestli je situace, kdy vodní pára ve výměníku kondenzuje, přínosná či nikoliv. Pokud ji shledáme přínosnou, ptejme se, jak je možné tento přínos vyjádřit kritérii, která pro posouzení výměníků pro zpětné získávání tepla ve vzduchotechnice používáme.
Teoretický rozbor
Kondenzace vodní páry, která je obsažená ve vlhkém vzduchu (dále jen vzduch) je proces, při kterém probíhá změna jejího skupenství z plynného na kapalné. Proces může probíhat na pevném povrchu stejně jako na hladině kapaliny a i ve vzduchu samotném. Hranicí určující vznik kondenzace je teplota rosného bodu tr, při které je vzduch nasycen vodními parami. Pro konkrétní stav vzduchu při konstantním atmosférickém tlaku existuje tedy unikátní teplota rosného bodu. Při konstantní teplotě vzduchu je závislá na podílu vodní páry ve vzduchu, s rostoucím podílem roste i teplota rosného bodu.
V případě tepelných výměníků uvažujeme, že povrchová teplota teplosměnné plochy ts je rozhodujícím kritériem pro vznik kondenzace vodní páry. Z porovnání obou teplot ts a tr lze popsat stavy, které shrnuje tabulka 1.
| Veličina | Stav bez kondenzace vodní páry | Stav s kondenzací vodní páry | Stav hrozící námrazy kondenzátu |
|---|---|---|---|
| Teplota | ts ≥ tr,i | ts < tr,i | ts < tr,i , ts < 0 °C |
| Parciální tlak vodní páry (sat – nasycený) | psat(ts) ≥ p(ti) | psat(ts) < p(ti) | psat(ts) < p(ti) |
| Měrná vlhkost | xsat ≥ xi | xsat < xi | xsat < xi |
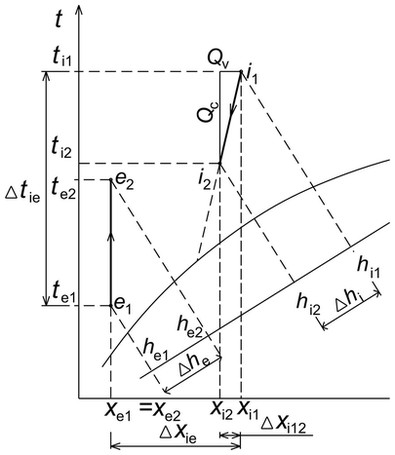
Výskyt kondenzace je ve výměníku ZZT obvykle lokální a nemusí nezbytně probíhat na stále stejném místě. Kondenzace vodní páry vznikající při běžných provozních stavech nemá vysokou intenzitu produkce vody. Zkondenzovaná vodní pára vytváří kapičky, případně velmi tenký film v porovnání s tloušťkou desky výměníku nebo šířkou průtočného kanálu. Ovšem mohou nastat stavy i s intenzivnější blánovou kondenzací, během které se na povrchu teplosměnné plochy vytvoří vodní vrstva, která při ztékání může zahltit průtočný kanál mezi deskami výměníku. Takový stav není v žádném případě přínosný, jelikož ovlivňuje průtok vzduchu výměníkem. Navíc stékající kondenzát dále ovlivňuje sdílení tepla ve výměníku. Stéká-li kondenzát po dlouhé dráze, může v jiném místě na teplosměnné ploše docházet k jeho zpětnému odparu do odpadního vzduchu a negativně ovlivňovat celkový sdělený tepelný tok po délce výměníku. Při teplotách blízkých 0 °C se tím ještě zvýší riziko namrzání. V každém případě je nezbytné zajistit rychlý odvod kondenzátu co nejkratší cestou mimo výměník. Na obrázku 1 je vyznačený průběh změn obou proudů vzduchu i a e v Mollierově diagramu.
Účinnosti
Pro posouzení vlivu kondenzace vodní páry na účinnost provozu výměníku ZZT jsou dále v textu použity čtyři základní účinnosti, pro sdílení tepla, pro sdílení citelného a vázaného tepla a exergetická. Každá z nich definuje poměr skutečně přeneseného tepelného toku z ochlazovaného vzduchu i do ohřívaného vzduchu e k potenciálnímu maximu tepelného toku mezi oběma proudy vzduchu.
Výpočetní vztahy pro účinnost sdílení tepla vychází z obecné rovnice (1).
kde
- η
- … účinnost sdílení tepla, [-]
- Q
- … skutečně přenesený tepelný tok, [W]
- Qmax
- … maximální tepelný tok, který lze získat mezi proudy vzduchu i a e [W]
Skutečně přenesený tepelný tok Q vyjádříme na základě rovnosti tepelného toku odevzdaného ochlazovaným vzduchem i a přijatého ohřívaným vzduchem e, čímž předpokládáme, že ve výměníku nedochází ke ztrátám tepla.
kde
- mi
- … hmotnostní průtok ochlazovaného suchého vzduchu, [kg.s−1]
- me
- … hmotnostní průtok ohřívaného suchého vzduchu, [kg.s−1]
- h
- … měrná entalpie (1 – vstup, 2 – výstup), [J.kg−1 s.v.]
Skutečně přenesený tepelný tok Q rozdělíme na složku citelného a vázaného tepla. Pro vyjádření vlivu kondenzace je toto zjednodušení velmi praktické, ačkoliv sdílení tepla i hmoty probíhá současně a vzájemně se ovlivňuje.
kde
- t
- … teplota vzduchu, [°C]
- cp,sv
- … měrná tepelná kapacita suchého vzduchu, [J.kg−1.K−1]
- cp,vp
- … měrná tepelná kapacita vodní páry, [J.kg−1.K−1]
- l23
- … skupenské teplo vypařování vody, [J.kg−1]
První část výrazu (3) popisuje v přeneseném tepelném toku Q zastoupení citelného tepla Qc, druhá část zastoupení vázaného tepla Qv uvolněného při kondenzaci vodní páry. Rovnicemi (2) a (3) lze vyjádřit dílčí přínosy citelného a vázaného tepla na růst entalpie ohřívaného vzduchu.
V čitateli rovnice (4) vyjadřuje druhý člen součtu změnu citelného tepla vodní páry daný poklesem teploty směsi vlhkého vzduchu, při kondenzaci vodní páry i poklesem jejího množství. V porovnání s citelným teplem suchého vzduchu je velmi malý a zanedbatelný.
Maximální tepelný tok, který lze teoreticky sdělit v nekonečně dlouhém protiproudém výměníku je definován rovnicí (6) [3] na základě rozdílu vstupních teplot ochlazovaného a ohřívaného vzduchu. Tuto formulaci použijeme pro vyjádření sděleného citelného tepla.
kde
- Cmin
- … minimální hodnota z průtočných tepelných kapacit ochlazovaného Ci = mi.cp,vv
a ohřívaného vzduchu Ce = me.cp,vv, [W.K−1] - cp,vv
- … měrná tepelná kapacita vlhkého vzduchu, [J.kg−1.K−1]
Maximální tepelný tok vázaného tepla je závislý na rozdílu měrných vlhkostí vstupních stavů ochlazovaného a ohřívaného vzduchu.
kde
- mmin
- … menší z hmotnostních průtoků mi a me, [kg.s−1]
Určení maximálního tepelného toku při sdílení celkového tepla vyžaduje úpravu rovnice (6) na tvar vyjádřený rozdílem měrných entalpií ochlazovaného a ohřívaného vzduchu.
Na základě rovnic (1), (3), (6), (7) a (8) je možné postupně vyjádřit vztahy pro jednotlivé účinnosti sdílení citelného, vázaného a celkového tepla.
Účinnost sdílení citelného tepla vyplývá z maximálního tepelného toku Qmax,c definovaného podle rovnice (6). Přenesený tepelný tok Qc vyjádříme jednodušším tvarem rovnice (3), ze které odebereme díl tepla z kondenzující vodní páry mi (xi1 − xi2) l23. Rovnici (3) lze ještě dále zjednodušit zanedbáním změny citelného tepla vodní páry. Potom vznikne vztah, který známe z literatury [3], [4].
Účinnost sdílení vázaného tepla je stanovená z maximálního tepelného toku Qmax,v (7). Přenesený tepelný tok Qv z části rovnice (3) vyjadřuje změnu měrné vlhkosti ochlazovaného vzduchu. Při zanedbání závislosti skupenského tepla vypařování vody l23 na teplotě jej lze v čitateli a jmenovateli zkrátit.
Účinnost sdílení tepla popisuje současný vliv citelného i vázaného tepla a vychází z rovnic (3) a (8).
Exergetická účinnost je definována obdobně jako předchozím poměrem skutečně přeneseného tepelného toku a možného maxima, které jsou vyjádřené exergií tepelných toků. Exergie tepelného toku vyjadřuje nejen množství sdíleného tepla, ale i jeho kvalitu ve smyslu jeho využitelnosti. V zásadě lze popsat tepelný tok sdílený mezi vyššími teplotami jako využitelnější než takový, který je sdílený mezi nižšími, i když teplotní spád je v obou případech shodný. Popisuje tedy potenciál jeho využití. Mezi obecné výhody exergetické analýzy patří její široký záběr při vyhodnocování chování zařízení, nebo celého systému. V analýze je možné zahrnout vedle sdílení citelného a vázaného tepla i vliv tlakového spádu, změny chemického potenciálu pracovní látky aj. Exergetickou účinnost ηex stanovíme podle rovnice (12) [5] a je dána dvěma dílčími účinnostmi popisujícími kvalitu sdílení tepla v jednotlivých proudech vzduchu.
kde
- ηex
- … exergetická účinnost, [-]
- ηex,i
- … dílčí exergetická účinnost využití tepla z ochlazovaného vzduchu i, [-]
- ηex,e
- … dílčí exergetická účinnost využití tepla v ohřívaném vzduchu e, [-]
- E
- … exergie tepelného toku proudu vzduchu na vstupu nebo výstupu výměníku, [W]
Stanovení obou dílčích exergetických účinností ηex,i a ηex,e je velmi přínosné pro zjištění, jak je využitý tok citelného tepla i navýšení tepelného toku při kondenzaci vodní páry ve výměníku mezi vstupem a výstupem ochlazovaného proudu vzduchu. Ve střední části rovnice (12) máme vyjádřené v součinu dílčí exergetické účinnosti, každá z nich vyjadřuje jak rozdíl exergií vzniklý v daném proudu vzduchu (i nebo e) je využitý k maximálnímu potenciálu. Pro účinnost ηex,i to znamená vyjádření velikosti tepelného toku sděleného z ochlazovaného vzduchu do teplosměnnnné plochy rozdílem exergií (Ei1 − Ei2). Vzniklý rozdíl exergií mezi vstupem a výstupem je vztažen k maximálnímu potenciálu danému exergií ochlazovaného vzduchu Ei1 na vstupu do výměníku. V případě účinnosti ηex,e stejná rovnice vyjadřuje, jak se tepelný tok (Ei1 − Ei2) projeví v ohřívaném proudu vzduchu e, tedy jak vzroste exergie ohřívaného vzduchu při průtoku výměníkem. Exergetická účinnost ηex tudíž vyjadřuje vliv sděleného tepelného toku do ohřívaného vzduchu popsaného rozdílem (Ee2 − Ee1) vztaženého k maximálnímu potenciálu.
Exergii tepelného toku definujeme podle rovnice (13), která odpovídá Bejanově rovnici [6] při zanedbání vlivu tlakové ztráty ve výměníku. Tlakovou ztrátu výměníku při průtoku vzduchu a nezbytný příkon ventilátorů zanedbáme, jelikož stejný vliv není postižen ani v jedné z výše popsaných účinností ηc, ηv a η.
kde
- T0, h0
- … termodynamická teplota a měrná entalpie popisující srovnávací stav okolí (dead state)
- T
- … termodynamická teplota vzduchu, [K]
Dosadíme-li rovnici (13) za jednotlivé exergie tepelných toků do rovnice pro exergetickou účinnost (12) a provedeme několik algebraických úprav, obdržíme vztah popisující závislost exergetické účinnosti na skutečně přeneseném tepelném toku Q.
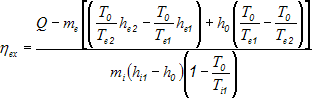 (14)
(14)
Podobně jako rovnici (14) lze vyjádřit dílčí exergetické účinnosti. Abychom se vyhnuli rozsáhlým rovnicím, nebudeme je zde uvádět.
Pro rekuperační výměník je možné stanovit bilanci exergií tepelných toků na vstupech a výstupech [7]. Pro její úplnost je nezbytné zavést exergii ztrátového tepelného toku ΔE, která vyjadřuje nevyužitou exergii v nevratném procesu podle 2. zákona termodynamiky.
Přepíšeme-li bilanci (15) rozdíly exergií tepelných toků ochlazovaného a ohřívaného vzduchu, poznáme, že exergie ztrátového tepelného toku bude klesat pouze, když změna exergie ohřívaného vzduchu ΔEe12 poroste více než ochlazovaného ΔEi12.
V závislosti na změně exergií tepelných toků a exergii ztrátového tepelného toku lze vyjádřit i rovnici pro dílčí exergetické účinnosti (12).
Exergetická analýza má podstatný požadavek, kterým je stanovení vztažné hranice, stavu okolí ke kterému jsou jednotlivé exergie definované. Nazývá se také „dead state“ a v textu jsou jeho stavové veličiny označeny indexem 0. Při běžné analýze se obvykle stanovuje pouze teplota T0, ale pokud chceme posuzovat vlhký vzduch při změnách obsahu vodní páry, musíme tuto hranici definovat jako každý jiný stav vzduchu třemi stavovými veličinami. Nejčastěji tlakem p0, který obvykle uvažujeme atmosférický, teplotou T0 a doplníme ještě měrnou vlhkost x0.
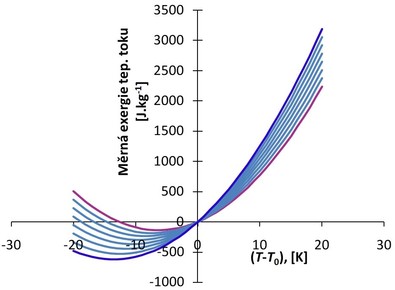
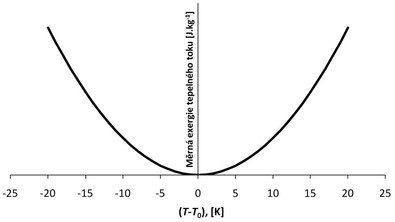
Obr. 3 Průběh kombinace vlivu volby teploty T0 a měrné vlhkosti x0 na měrnou exergii tepelného toku e = E/m (pro stav vzduchu T = 293,15 K, x = 5 g.kg−1 s.v.)
Volba stavu okolí výrazně ovlivní velikost jednotlivých exergií tepelných toků, proto je nutné volit jeho parametry zodpovědně. Velmi zajímavou diskuzi k volbě parametrů stavu okolí pro exergetickou analýzu rekuperačního výměníku při sdílení citelného tepla nalezneme v článku Dr. Boelmanové [8]. Základní problém spočívá ve vzdálenosti stavu okolí od posuzovaného stavu. Když je teplota T0 rovna teplotě T, je podle rovnice (13) exergie tepelného toku nulová. Pokud rozdíl T a T0 roste, zvyšuje se i měrná exergie tepelného toku (obr. 2).
Uvážíme-li však vliv volby měrné vlhkosti x0 v parametrech stavu okolí, zjistíme výrazné odchylky od průběhu zobrazeného v grafu na obrázku 2. Na obrázku 3 je ukázána závislost měrné exergie tepelného toku vlhkého vzduchu na volbě teploty T0 a měrné vlhkosti x0. Z průběhu vyplývá, že při T < T0 jsou hodnoty měrné exergie tepelného toku vlhkého vzduchu záporné a minimum křivek měrné exergie tepelného toku se posouvá k vyšším rozdílům (T − T0).
(Fialová čára pro x0 = 0 g.kg−1 s.v., tmavomodrá čára pro x0 = 5,6 g.kg−1 s.v., mezilehlé se liší o 0,8 g.kg−1 s.v.)
Pozn.: některé kombinace T0 a x0 jsou teoretické, neboť popisují stavy daleko za mezí sytosti a slouží jen pro demonstraci trendu závislosti.
Při exergetické analýze tepelných výměníků se převážně vyhodnocují rozdíly exergií tepelných toků na vstupu a výstupu vzduchu. Při teplotách vzduchu blízkých volené teplotě okolí budou rozdíly exergií menší než při teplotách vzdálenějších. Důsledek je patrný z tvaru křivky zobrazené na obr. 2, který se stane výraznějším v závislosti na volbě x0 (obr. 3). Tím budou ovlivněny výsledky bilanční rovnice (15) a i exergetických účinností (12), (14). Z toho vyplývá, že není vhodné volit teplotu T0 ani měrnou vlhkost x0 vyšší než kteroukoliv z teplot a vlhkostí proudů vzduchu vyskytujících se při provozu výměníku.
Z těchto důvodů je nezbytné interpretovat a prezentovat výsledky vždy s ohledem na volené podmínky stavu okolí. Nevýhodou exergetické analýzy je obtížné srovnání výsledků vypočtených při různých podmínkách stavu okolí (dead state), byť by se jednalo o stejný výměník tepla.
Teoretický vliv kondenzace vodní páry
V rovnicích (2) až (5) uvažujeme, že tepelný tok přenesený z ochlazovaného proudu vzduchu do ohřívaného zahrne celé sdílené citelné i vázané teplo. V následující části popíšeme, jak se vázané teplo uvolněné při kondenzaci vodní páry může projevit na chování výměníku z pohledu jednotlivých účinností. Uvažujme teoretický provozní stav rekuperačního výměníku, kterým proudí shodné množství ochlazovaného i ohřívaného vzduchu. Následující tabulka 2 shrnuje základní parametry stavů vzduchu. Výstupní stavové veličiny jsou vypočítány z rovnic (2) a (3), hodnoty cp,sv, cp,vp a l23 jsou uvažovány shodné pro oba proudy vzduchu a nezávislé na teplotě.
| Stav bez kondenzace v. p. | Hmotnostní průtok [kg.s−1] | Vstup/výstup | Teplota [°C] | Měrná vlhkost [g.kg−1] |
|---|---|---|---|---|
| ochlazovaný vzduch i | 0,2 | vstup i1 | 21 | 8 |
| výstup i2 | 11 | 8 | ||
| ohřívaný vzduch e | 0,2 | vstup e1 | 2 | 2,5 |
| výstup e2 | 12,15 | 2,5 |
Pro vyjádření vlivu kondenzace vodní páry je uvažován teoretický rozsah poklesu měrné vlhkosti (xi1 − xi2) ochlazovaného vzduchu 0 až 1,5 g.kg−1 s.v. Podle rovnice (5) můžeme vypočítat přínos změny skupenství vodní páry na růst měrné entalpie ohřívaného vzduchu. Proti stavu bez kondenzace dojde k navýšení přeneseného tepelného toku Q. To se projeví i v čitatelích rovnic (10), (11), (14) a v důsledku k nárůstu uvažovaných účinností.
Ochlazovanému vzduchu i v důsledku rostoucího rozdílu (xi1 − xi2) klesá výstupní měrná entalpie hi2. Navýšení tepelného toku o Qv se projeví v ohřívaném vzduchu růstem entalpie he2, ze které je dopočítána změna teploty te2 (Tab. 3). V tabulce 3 je vyjádřené rozložení vlivu citelného a vázaného dílu sděleného tepelného toku na výstupní teplotu ohřívaného vzduchu te2. Závislost růstu teploty te2 na změně (xi1 − xi2) je lineární a na každý 1 gram zkondenzované vodní páry na kilogram suchého vzduchu se v uvažovaném případě zvýší teplota ohřívaného vzduchu te2 na výstupu o 2,5 °C.
Rozdíly Δte,c zahrnují i vliv změny citelného tepla vodní páry v přeneseném tepelném toku, který zvýší Δte,c o 0,1 až 0,13 K. V posledním sloupci tabulky 3 je vidět nárůst přeneseného tepelného toku Q od stavu bez kondenzace až po stav s nejvyšším rozdílem měrné vlhkosti, tj. 1,5 g.kg−1 s.v. Mezi krajními uvažovanými stavy dojde k nárůstu Q o 783 W, jeho závislost na změně (xi1 − xi2) je opět lineární a na každý 1 g.kg−1 s.v. je sděleno do ohřívaného proudu vzduchu 502 W.
(xi1 − xi2) [g.kg−1 s.v.] | Výstupní stavy vzduchu | Změna teploty ohřívaného vzduchu | ||||||
|---|---|---|---|---|---|---|---|---|
| xi2 [g.kg−1 s.v.] | hi2 [J.kg−1 s.v.] | he2 [J.kg−1 s.v.] | te2 [°C] | Δte [K] | Δte,cit [K] | Δte,vaz [K] | QR [W] | |
| 0 | 8 | 31218,7 | 18515,3 | 12,15 | 10,15 | 10,15 | 0,00 | 2039,8 |
| 0,4 | 7,6 | 30210,5 | 19528,1 | 13,15 | 11,15 | 10,16 | 1,00 | 2241,4 |
| 0,8 | 7,2 | 29202,3 | 20541,0 | 14,15 | 12,15 | 10,16 | 1,99 | 2443,0 |
| 1,2 | 6,8 | 28194,1 | 21553,8 | 15,16 | 13,16 | 10,17 | 2,99 | 2644,7 |
| 1,5 | 6,5 | 27438,0 | 22313,5 | 15,91 | 13,91 | 10,18 | 3,73 | 2795,9 |
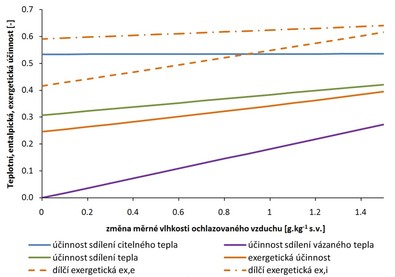
V důsledku zvyšování Q při kondenzaci vodní páry se lineárně zvyšují i uvažované účinnosti vyjma účinnosti sdílení citelného tepla. Tyto trendy demonstruje graf na obrázku 4, kde je zobrazená závislost jednotlivých účinností na rozdílu měrné vlhkosti v proudu ochlazovaného vzduchu mezi vstupní xi1 a výstupní xi2.
Účinnost ηc je v zásadě konstantní, sdílený tepelný tok citelného tepla je stálý s drobným nárůstem o změnu citelného tepla vodní páry v ochlazovaném vzduchu. Tepelný tok vázaného tepla Qv narůstá od nulové hodnoty a s ním roste i účinnost sdílení vázaného tepla ηv. V rovnici (10) se zvyšuje rozdíl (xi1 − xi2), který využívá malou část teoretického maxima daného rozdílem (xi1 − xe1) (obr. 1), čemuž odpovídá maximální hodnota účinnosti ηv = 27,3 %. Přesto se kondenzace vodní páry výrazně projeví na účinnosti sdílení tepla η. Od počátečního stavu, při kterém by měl výměník ZZT účinnost sdílení tepla 30,6 %, vzrostla díky změně skupenství vodní páry 1,5 g.kg−1 s.v. až na 42 %. Teoretický nárůst o 11,4 % díky tepelnému toku vázaného tepla není zanedbatelný.
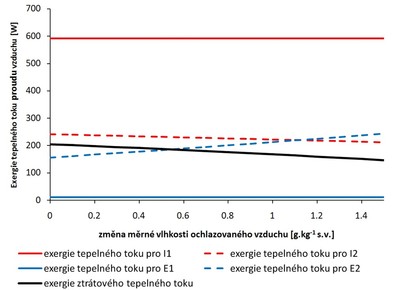
Pro výpočet exergií a exergetických účinností podle rovnic (12) a (13) byl uvažován stav okolí o teplotě T0 = 273,15 K a měrné vlhkosti x0 = 0 g.kg−1 s.v., které jsou nižší než veličiny proudů vzduchu na vstupech a výstupech výměníku. Průběhy exergií tepelných toků jsou v závislosti na změně měrné vlhkosti v ochlazovaném vzduchu zobrazené na obr. 5. Je patrné, že s rostoucí intenzitou kondenzace vodní páry roste využití potenciálu energie z ochlazovaného proudu vzduchu.
Pro hodnocení je důležitý výpočet exergie ztrátového tepelného toku ΔE (15), vyjadřující nevyužitý potenciál exergie tepelného toku z ochlazovaného vzduchu na vstupu do výměníku. S vyšším podílem ΔE v bilanci dochází ve výměníku k vyšší disipaci energie, která mohla být využitá v tepelném toku přeneseném do ohřívaného vzduchu. Z výsledků na obr. 5 zjišťujeme, že při kondenzaci vodní páry exergie ztrátového tepelného toku klesá. Její pokles přímo ovlivňuje výstupní exergie Ei2, která se snižuje a Ee2, která roste.
Obě dílčí exergetické účinnosti jsou přímo závislé na exergii ztrátového tepelného toku ΔE (17), (18), (19). Pro zajištění jejich růstu musí ΔE klesat a zároveň ΔEe12 růst a to více než roste ΔEi12. Když ΔEe12 roste více než ΔEi12, vyplývá z toho vyšší tepelný tok sdělený z ochlazovaného vzduchu na teplosměnné ploše výměníku.
Dílčí exergetická účinnost využití tepla z ochlazovaného vzduchu ηex,i v souladu s rovnicí (17) roste velmi pozvolně. I při maximální uvažované změně měrné vlhkosti ochlazovaného proudu vzduchu je stále využita pouze část potenciálu vázaného tepla daného měrnou vlhkostí ochlazovaného proudu vzduchu na vstupu (xi1 = 8 g.kg−1 s.v.). Ohřívaný vzduch přesto přijímá zvýšený tepelný tok o skupenské teplo kondenzace. Navýšení přínosu se v ohřívaném vzduchu projeví nárůstem rozdílu exergií tepelných toků mezi výstupem a vstupem ΔEe12 o 60 %. Vztáhneme-li jej k potenciálu ΔEi12 odevzdanému ochlazovaným vzduchem teplosměnné ploše podle rovnice (18), je jeho podíl natolik významný, že ΔEe12 má díky kondenzaci vyšší růst než ΔEi12, a tudíž dílčí exergetická účinnost využití tepla v ohřívaném vzduchu ηex,e roste v uvažovaném intervalu změny měrné vlhkosti rychleji než ηex,i.
Exergetická účinnost má trend podobný účinnosti sdílení tepla, neboť vztahuje skutečně získaný přínos v ohřívaném vzduchu k maximálnímu potenciálu exergie Ei1.
Při pohledu na celkovou bilanci exergií tepelných toků výměníku můžeme ukázat výhody exergetické analýzy. Z pohledu rozboru dalšího energetického potenciálu při provozu výměníku jsou podstatné exergie tepelného toku ochlazovaného vzduchu Ei2 na výstupu a exergie ztrátového tepelného toku ΔE. Exergie Ei2 vyjadřuje potenciál, který odchází v proudu ochlazovaného vzduchu mimo další možnost jeho využití. Z obr. 5 je zřejmé, že ani při vyšší míře kondenzace vodní páry nedošlo k výraznějšímu poklesu Ei2, pouze o 12 %. Tudíž v ochlazovaném vzduchu je stále značný potenciál energie. Této znalosti můžeme například využít, když bychom sériově zapojili dva výměníky ZZT. Potom můžeme analyzovat přínosy jednotlivých výměníků i celé sestavy, řešit rozložení přeneseného tepelného toku mezi jednotlivé výměníky a optimalizovat jejich provoz.
Vyčíslením exergie ztrátového tepelného toku ΔE vyjadřujeme nevratnou změnu energie. Ve výměníku probíhá rozdělení počátečního potenciálu ochlazovaného vzduchu Ei1 na jednotlivé složky (15), nevratná ztráta ΔE je významná. Při kondenzaci vodní páry a využití zvýšeného tepelného toku lze její zastoupení snížit a zvýšit požadovanou exergii tepelného toku ohřívaného vzduchu Ee2 na výstupu. Z předchozího popisu vyplývá, že ΔE významně ovlivňuje exergetickou účinnost zařízení pro zpětné získávání tepla, proto je vhodná pro posouzení účinnosti při různých provozních stavech. Exergetické účinnosti nabízí pohled na kvalitu využití energetického potenciálu samostatně na straně ochlazovaného a ohřívaného vzduchu. Při analýze provozu výměníku jimi můžeme rozpoznat, který z proudů vzduchu více využívá svého potenciálu, a který méně. V následné optimalizaci provozu můžeme navrhovat příslušná opatření.
Závěr
V článku byl teoreticky diskutován vliv kondenzace vodní páry ve výměníku pro zpětné získávání tepla. Její vliv při posuzování celkové bilance výměníku lze shledat jako pozitivní, přestože v běžném výměníku ZZT, kde jsou proudy vzduchu odděleny, je při kondenzaci využitá pouze malá část vázaného tepla vodní páry. Přínosné závěry přináší exergetická analýza, která ukazuje, že ochlazovaný vzduch na výstupu z výměníku stále nese významný potenciál energie. Rozborem exergie ztrátového tepelného toku a exergetických účinností lze popsat možné zlepšení účinnosti provozu výměníku ZZT.
Poděkování
Tento příspěvek vznikl z podpory grantu GAČR 103/08/P358 „Metoda hodnocení efektivnosti zařízení pro zpětné získávání tepla ve větracích systémech metodou exergie tepelných toků“.
Použité zdroje
- [1] Kabele, K., et al., Energetická náročnost budov a vzduchotechnika. Vytápění, větrání, instalace, 2010, roč. 19, č. 3, s. 131–136
- [2] Morávek, P., Moderní koncepce pasivní výstavby v podmínkách ČR. Vytápění, větrání, instalace, 2006, roč. 15, č. 1, s. 19–24
- [3] Shah, R. K., Seculic, D. P., Fundamentals of heat exchanger design. J. Wiley and Sons, New Jersey, 941, 2003
- [4] Incropera, F. P., et al., Fundamentals of heat and Mass Transfer. New York: John Wiley and Sons, Inc., 2007, 997 s., 6th edition, ISBN 978-0-471-45728-2
- [5] Adamovský, D., et al., Exergy of Heat Flows in Exchanger Consisting of Gravity Heat Pipes. Research in Agriculture Engineering, 2005, roč. 51, č. 3, s. 81–87
- [6] Bejan, A., Advanced Engineering Thermodynamics. New York: John Wiley and Sons, Inc., 1997, 850 s., 2nd edition, ISBN 0-471-14880-6
- [7] Adamovský, D., Adamovský, R., Rutkowski, K., R., Modification of the method for the assessment of heat exchangers for the recuperation of heat from ventilation air. Annual Review of Agricultural Engineering, 2009, roč. 2008, č. 8, s. 17–28.
- [8] Boelman, E.C., Sakulpipatsin, P., Critical analysis of exergy efficiency definitions applicable to buildings and building services. In: Proceedings of Plea2004 – The 21th Conference on Passive and Low Energy Architecture, Eindhoven, 2004, s. 6. ISBN 9038616368.
Condensation of water vapor in regular heat recovery heat exchangers is not an exceptional state, but its influence is usually neglected. In the article is described possible efficiency increase due to rise of transferred heat flux between cooled and heated air stream caused by latent heat from condensation of water vapor contained in air.