Zkušenosti s provozem tepelných čerpadel 8.: Teplotní spád a průtok primárním okruhem TČ země/voda
Úspornost tepelného čerpadla závisí i na optimálním návrhu primárního sběrače tepla, nejčastěji ve formě vrtu, plošného kolektoru, ale též i slinek či energetických košů. Délka potrubí a jeho dimenze těsně souvisí s provozním teplotním spádem v primárním okruhu tepelného čerpadla.
V článku „Zkušenosti s provozem tepelných čerpadel 6.: Návrhový teplotní spád a průtok otopné vody“ byla hlavní pozornost věnována souvislostem mezi teplotními poměry, které panují v sekundární části pracovního okruhu, na tepelném výměníku – kondenzátoru tepelného čerpadla a schopnostem chladiva předávat teplo při jeho kondenzaci do otopné vody. V tomto článku je pozornost zaměřena na opačnou, tedy primární část pracovního okruhu tepelného čerpadla, které získává tepelnou energii z přírodního prostředí prostřednictvím cirkulující kapaliny. Analyzovány jsou teplotní poměry, které panují na tepelném výměníku – výparníku, jehož účelem je převádět tepelnou energii získanou z jejího přírodního zdroje do chladiva a jak tyto poměry ovlivňují energetickou efektivitu provozu tepelného čerpadla.
1. Návrhový teplotní spád primárního okruhu
Běžně používaný teplotní spád nízkotuhnoucí kapaliny – nemrznoucí směsi cirkulující v primárním okruhu tepelných čerpadel země/voda určených pro vytápění je 2 až 5 K (Kelvin, v případě rozdílu teplot je hodnota číselně shodná s rozdílem teplot ve °C). Doporučuje se, aby za teplot nemrznoucí směsi na vstupu do výparníku cca 0 °C byl spád okolo 3 K a za teplot primáru 10 až 15 °C na vstupu do výparníku byl spád do 5 K. Vyšší teplotní spád se obecně nedoporučuje, vyjma specifických aplikací s vyššími teplotami nemrznoucí směsi na vstupu do TČ, jejichž příkladem může být rekuperace odpadního tepla z průmyslu, v potravinářství atd.).
Proč tomu tak je? Důvodem je, že při rostoucím teplotním rozdílu na primárním okruhu klesá tzv. vypařovací teplota (v článku zmiňována jako JR0), jelikož klesá výstupní teplota nemrznoucí směsi z výparníku. Pro energetickou efektivitu provozu tepelného čerpadla jde o významný fakt, protože největší část tepla, které cirkulující nemrznoucí směs přináší z přírodního prostředí přechází do chladiva právě při jeho vypařování. Jak bylo vysvětleno i v jiných článcích, tak vypařovací teplota chladiva závisí na působícím tlaku a se snižováním vypařovací teploty se zvyšuje spotřeba práce kompresoru a snižuje se energetická efektivita provozu tepelného čerpadla.
Vypařovací teplotu chladiva (a z druhé strany pohledu stejně tak i kondenzační teplotu) určuje tlak, který na chladivo působí – resp. v kompresorovém okruhu na chladivo tlakem působí pouze a jen to samé chladivo a tlak je dán teplotou. Změřit aktuální vypařovací teplotu příložným čidlem v praxi přímo neumíme. Při uvádění tepelných čerpadel do povozu a jejich servisu však můžeme pracovat s tlakem, který umíme tlakoměry měřit jednoduše a přesně. Pro každé používané chladivo je závislost vypařovací teplota – vypařovací tlak přesně změřena a známá a dostupná buď v grafické formě, formě tabulek, anebo ji dokonce již obsahuje software speciálních tlakoměrů určených pro použití s tepelnými čerpadly, resp. chladicími stroji obecně. Proto v praxi můžeme relativně jednoduchým měřením tlaku určovat vypařovací teplotu chladiva v různých provozních stavech tepelného čerpadla.
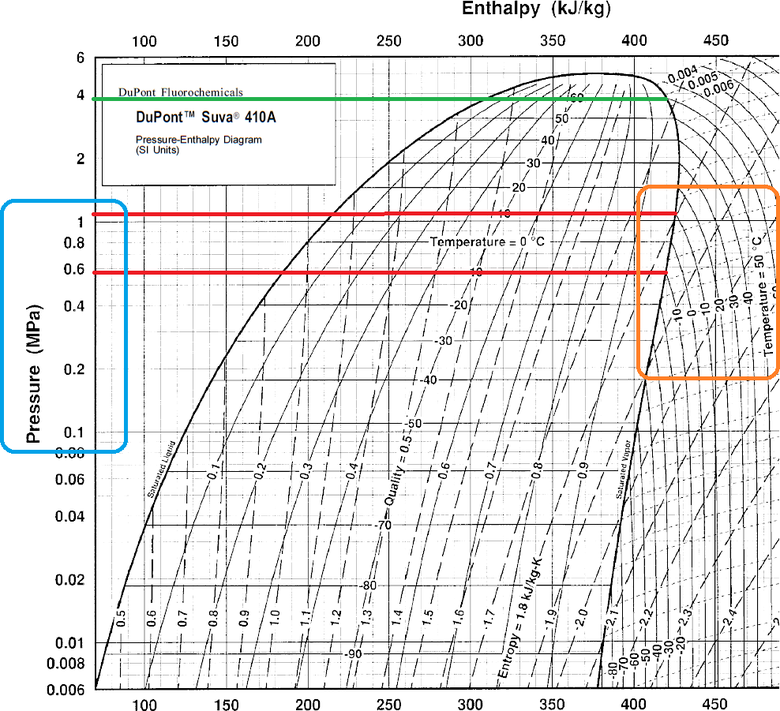
Obr. 1 Příklad graficky vyjádřené závislosti vypařovací teploty a tlaku pro chladivo R410A v P(log)-h diagramu. Červenými linkami je zachycena vypařovací teplota −10 °C, které odpovídá vypařovací tlak cca 5,7 bar, a vypařovací teplota +10 °C, které odpovídá vypařovací tlak cca 10,8 bar (pozn. pro odborníky: se zanedbáním teplotního skluzu cca 0,15 K tohoto chladiva). Pro názornost je zeleně vyznačen i vypařovací tlak cca 38 bar, kterému odpovídá vypařovací/kondenzační teplota 60 °C, která je s chladivem R410A většinou limitní. (Graf: DuPont)
Čím nižší je vypařovací teplota, tím nižší je i vypařovací tlak a tím pádem roste tlakový rozdíl a poměr (výtlačný vs. sací tlak), který musí kompresor překonávat. Tím větší následně bude i spotřeba elektrické energie na pohon kompresoru. Proto není vhodné pro danou teplotu zpátečky nemrznoucí směsi do výparníku příliš „šetřit“ na jejím průtoku, protože se snažíme udržet vypařovací teplotu/tlak co nejvýš s cílem zajistit co nejnižší spotřebu kompresoru. I pro primární okruh s nemrznoucí směsí platí pro přenos stejného množství tepelné energie Q klasická rovnice
ze které vidíme, že mezi rozdílem teplot T2 − T1 a velikostí průtoku, ve vzorci průtok zastupuje hmotnost nemrznoucí směsi m, je přímá úměra. Kolikrát klesne rozdíl teplot, tolikrát vzroste průtok. Mírné zvýšení příkonu oběhového čerpadla v primárním okruhu je však více než vyváženo sníženou prací kompresoru.
Jestliže se na kondenzátoru snažíme mít kondenzační teplotu JR1 co nejblíž výstupní teplotě otopné vody TC3 (viz předchozí 6. díl), tak se analogicky snažíme mít vypařovací teplotu chladiva JR0 co nejblíže teplotě zpátečky nemrznoucí směsi TB0, aby vypařovací teplota byla teplotně co nejblíž primárnímu zdroji tepla.
Rozdíl teplot TB0 − JR0 na výparníku však NIKDY nemůže být tak malý jako rozdíl teplot na kondenzátoru JR1 − TC3, protože musíme na výparníku dodržet určité minimální, ale bezpečné přehřátí par chladiva TR5 − JR0. Toto přehřátí vytváří bezpečnostní rezervu chránící kompresor před nasátím kapalného chladiva. Chladivo za expanzním ventilem se nachází ve stavu srovnatelném s vodní mlhou, tedy ve formě rozprášených velmi jemných kapiček kapalného chladiva a teprve tyto kapičky se ve výparníku při styku s jeho stěnami nebo při styku s již vzniklými parami chladiva mění na páru. Proto je možné, že se při nedostatečném přehřátí do kompresoru dostane kapička chladiva, která se v kompresoru při zvýšení teploty následkem stlačování odpaří a tím nadměrně vzroste tlak v kompresoru. Tak vznikají tzv. kapalinové rázy, které mohou skončit až totální mechanickou destrukcí kompresoru.
Vzhledem k nutnému přehřátí chladiva však nemá smysl snažit se dosáhnout na primárním okruhu velmi vysokého průtoku nemrznoucí směsi s cílem přiblížit se s teplotou JR0 teplotě TB0 např. až na 1 K.
2. Vliv změny průtoku nemrznoucí směsi výparníkem TČ země/voda při konstantní teplotě zpátečky
Jak se mění vypařovací teplota chladiva JR0 v závislosti na průtoku nemrznoucí směsi při konstantní teplotě zpátečky TB0 je znázorněno na grafech na obr. 1.
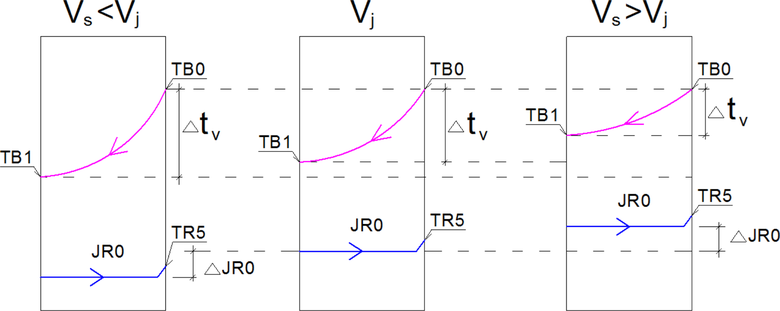
Obr. 2 Vliv velikosti průtoku nemrznoucí směsi Vs výparníkem tepelného čerpadla země/voda na průběh teplot ve výparníku při konstantní teplotě TB0 zpátečky nemrznoucí směsi v porovnání se stavem při jmenovitém průtoku Vj (uprostřed)
V obrázku 2. jsou znázorněny teplotní poměry na výparníku, kdy nízkotuhnoucí směs protéká výparníkem zprava doleva a chladivo protiproudně zleva do prava. Fialová křivka reprezentuje průběh teploty nemrznoucí směsi, která se při průtoku výparníkem ochlazuje z teploty TB0 na TB1. Modrá křivka prezentuje teplotu chladiva, které se vypařuje za teploty JR0 a následně se studené páry chladiva přehřejí na teplotu TR5. Rozdíl TR5 − JR0 je tzv. přehřátí, které musí být vždy kladné, aby si kompresor nenasál kapalnou fázi chladiva.
Když je skutečný průtok výparníkem Vs menší (na obr. 2 graf vlevo) než jmenovitý Vj (na obr. 2 graf uprostřed), při stejné vratné teplotě nemrznoucí směsi TB0, klesne výstupní teplota směsi TB1, protože z menšího množství protékající nemrznoucí směsi do chladiva přestoupí stejné množství tepla (pozn.: jak klesne výstupní teplota TB1, tak ve skutečnosti klesne i chladicí výkon stroje, tedy množství tepla přestupujícího z nemrznoucí směsi do chladiva). Proto také klesne vypařovací teplota/tlak JR0. Když je naopak skutečný průtok výparníkem Vs větší než jmenovitý Vj (na obr. 2 vpravo), bude dosaženo vyšší teploty TB1, tedy i vyšší vypařovací teploty/tlaku JR0. Zvýšením průtoku nemrznoucí směsi přes výparník pro danou teplotu zpátečky TB0 tedy sice vzroste vypařovací teplota/tlak JR0, ale to nemusí vždy automaticky znamenat nárůst topného faktoru. Protože při zvýšení průtoku nemrznoucí směsi se sice mírně zvýší vypařovací teplota, ale na druhé straně i mírně vzroste příkon oběhového čerpadla, a to se do výpočtu topného faktoru promítne naopak negativně. Záleží tedy na vzájemném poměru kladných a negativních souvislostí. Obecně by samozřejmě měl topný faktor stroje vzrůst.
3. Vliv vypařovací teploty chladiva na příkon kompresoru
Uvažujme, že poroste teplota TB0 jak se ohřívá plošný kolektor TČ země/voda s příchodem jara, které přináší oteplení spolu se srážkami. Zároveň uvažujme, že TČ bude „produkovat“ konstantní teplotu otopné vody na výstupu z kondenzátoru TC3. Takže roste TB0 za stále stejné teploty TC3. V tu chvíli byste čekali, že bude klesat AKUTÁLNÍ příkon kompresoru ve Wattech, protože TČ čerpá teplo z vyšší teplotní úrovně nízkopotenciálního zdroje tepla, a tak musí zákonitě růst aktuální topný faktor, respektive i průměrný celoroční topný faktor SPF (sezonní topný faktor reálné instalace). Omyl, AKTUÁLNÍ příkon kompresoru ve wattech vzroste.
Při stále stejné výstupní teplotě otopné vody TC3 a vyšší teplotě zpátečky primárního okruhu TB0 u TČ země/voda vzroste AKTUÁLNÍ příkon kompresoru ve Wattech.
Tento závěr nyní zřejmě narušil Váš pohled na tuto problematiku. Když se snížil rozdíl mezi vypařovací a kondenzační teplotou chladiva, měl by přece příkon kompresoru klesnout. Ale nebojte, vše je v pořádku. Jak totiž roste teplota TB0, roste i vypařovací teplota JR0, ale už málokdo ví, že s růstem vypařovací teploty narůstá i hustota par na sání kompresoru.
Pro orientační představu, hustota sytých par v současnosti nejvíce používaného chladiva R410A v tepelných čerpadlech se při růstu teploty par z −5 °C na +5 °C zvyšuje z cca 26 kg/m3 na 36 kg/m3 [2].
Každý kompresor má určitý objem pracovního prostoru. Do pracovního prostoru tedy nasaje jeho objemu odpovídající množství par chladiva, a toto množství pak stlačí. To znamená, že když mají páry chladiva s vyšší vypařovací teplotou vyšší hustotu, tak se do daného pracovního prostoru kompresoru nasaje větší hmotnostní množství par chladiva. Tento fakt způsobí, že kompresorem prochází zvýšené hmotnostní množství chladiva. A na jeho stlačení se zvýší příkon kompresoru.
Vyšší hustota par chladiva na sání kompresoru při jeho konstantních otáčkách znamená vyšší hmotnostní průtok chladiva, a tedy i vyšší AKTUÁLNÍ příkon kompresoru ve Wattech.
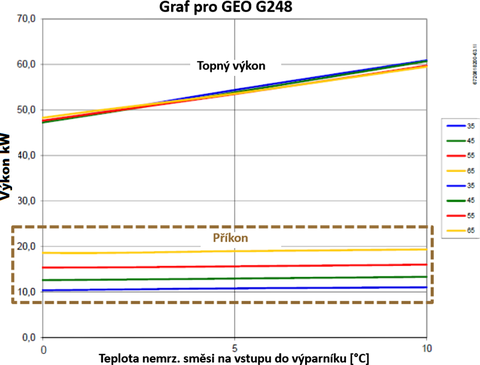
Obr. 3 Příklad grafu závislosti příkonu a výkonu TČ země/voda na teplotě nemrznoucí směsi v primárním okruhu před vstupem do výparníku pro různé teploty otopné vody na výstupu z TČ
To by mohlo vyvolat dojem, že je na hlavu postavena teorie, která nám léta letoucí říká, že TČ má tím menší spotřebu elektrické energie v kWh, čím vyšší je teplota nizkopotenciálního zdroje tepla. Nemějte obavy, teorie stále platí, vyšší teplota nízkopotenciálního zdroje tepla opravdu znamená nižší spotřebu elektrické energie na dodávku tepla tepelným čerpadlem. Proto je s takovým důrazem uvedeno, že s růstem teploty TB0 roste AKTUÁLNÍ příkon. Aktuálně totiž kromě příkonu kompresoru naroste i topný výkon na kondenzátoru stroje. Neboť, jak bylo zmíněno, aktuálně vzrostlo i hmotnostní množství stlačovaného chladiva, a tedy i množství tepla, které chladivo předá v kondenzátoru. Zásadní je, že za těchto podmínek topný výkon přenášený chladivem roste významně rychleji než příkon kompresoru (viz obr. 3). Z grafu je zřejmé, že jestliže v daných podmínkách topný výkon vrostl z cca 47 kW na 60 kW, tak příkon kompresoru se mění jen v jednotkách kW. Proto s růstem teploty TB0 roste nejen okamžitý topný faktor stroje, ale následně i průměrný sezónní SPF reálné instalace.
Výše uvedené je též podstatnou částí zdůvodnění, proč u tepelných čerpadel vzduch/voda tak výrazně klesá topný výkon s poklesem teploty venkovního vzduchu i když na výstupu je stále stejná teplota otopné vody.
4. Vliv průtoku nemrznoucí směsi na odběr tepla ze země
Topný výkon TČ země/voda je mimo jiné závislý na teplotě a průtoku nemrznoucí směsi na primárním okruhu. Vliv teploty byl popsán výše. Podívejme se nyní blíže na velikost průtoku nemrznoucí směsi, neboť ten významně ovlivňuje samotný tepelný výkon sběrače přírodního tepla vytvořeného ve formě vrtu, plošného kolektoru, ale též i slinek nebo energetických košů. Takže na jedné straně primárního okruhu tepelného čerpadla je tepelný výkon výparníku a na druhé straně tepelný výkon primárního sběrače tepla. Pokud tyto výkony nejsou srovnatelné a za daných provozních podmínek co nejvyšší, vzniká nerovnováha. Tu je nutné uhradit buď ve formě zbytečně zvýšených nákladů na sběrač tepla, zbytečně velký výparník a také snížením energetické efektivity tepelného čerpadla. Například čím nižší je průtok nemrznoucí směsi v primárním okruhu TČ země/voda, tím menší jsou turbulence v nemrznoucí směsi proudící potrubím a snižuje se intenzita přestupu tepla mezi stěnou potrubí a směsí. Tím větší je tepelný odpor, který zhoršuje přestup tepla z okolní zeminy do vrtu a dále do nemrznoucí směsi. Velmi dobře popsáno je to zde [1]. Je zřejmé, že i návrhu primárního okruhu je nutné věnovat velkou pozornost, pokud chceme od tepelného čerpadla maximální úspory.
5. Nestejné tlakové ztráty potrubních okruhů
V souvislosti s průtokem nemrznoucí směsi na primáru je vhodné zmínit další zajímavý fenomén, který je spojen s TČ země/voda s frekvenčně řízenými kompresory nebo se stroji, které mají např. 2 kompresory spínané on/off a které tak mohou část roku běžet pouze na jeden kompresor. Primární okruh TČ složený z více potrubních smyček (nyní uvažujme vrty) se výkonově i hydraulicky navrhuje na výkon, který je odvislý od tepelné ztráty budovy při výpočtové venkovní teplotě (nejčastěji −12, −15 a −18 °C). Aby každým vrtem protékalo, pokud možno, stejné množství nemrznoucí směsi, když jsou vrty sice stejně dlouhé, ale různě vzdálené od společného sběrače v šachtě, do každé smyčky se instalují regulační armatury a ty se podle potřeby nastaví. Tak se zajistí rovnoměrný odběr tepla ze všech vrtů a jejich teplotní vyváženost. Toto vše platí pro návrhový průtok nemrznoucí směsi.
Pokud se sníží potřeba tepla a s tím poklesne i zatížení kompresoru, např. pouze na 60 % a regulace oběhového čerpadla v primárním okruhu zajistí adekvátně nižší průtok nemrznoucí směsi odpovídající požadovanému teplotnímu spádu mezi vstupem nemrznoucí směsi do výparníku a výstupem z něj, tak se bez přestavení regulačních ventilů stejnoměrné zatékání do různě vzdálených vrtů od šachty naruší a nebude odpovídat projektu.
Pro návrh regulačního ventilu platí základní vzorec:
kde je
- Q
- průtok [m3/h]
- Δp
- tlaková ztráta na ventilu [bar]
- kv
- průtokový součinitel [m3/h] odpovídající konstrukci ventilu.
Již z uvedeného základního vzorce vidíme, že vztah mezi průtokem a tlakovou ztrátou na ventilu, pomocí které jsme vyrovnali nerovnováhy průtoků nemrznoucí směsi v různě vzdálených vrtech, není jednoduchý, lineární. Pokud při snížené potřebě tepla poklesne celkový průtok nemrznoucí směsi, projeví se to změnami průtoků v jednotlivých smyčkách odlišně. Blíže umístěné vrty se přetěžují větším průtokem na úkor vzdálenějších. Odnímá se z nich více tepla a bližší vrty se proto více ochlazují. A protože průtok bližšími vrty je větší než vzdálenějšími, po smíchání nemrznoucí směsi ze všech vrtů je její výsledná teplota nižší, než by mohla být při vyrovnaném proudění. V tu chvíli se tedy na výparník TČ dostává o něco nižší teplota nemrznoucí směsi, než by tomu bylo, kdyby byly do odběru tepla ze země zapojeny všechny vrty rovnoměrně tak, jak bylo s naprostou samozřejmostí plánováno v projektu. TČ následně dosahuje nižších hodnot okamžitého i průměrného sezónního topného faktoru COP/SPF, než by jinak mohlo.
Stejného průtoku nemrznoucí směsi všemi vrty různě vzdálenými od šachty se společným sběračem při měnícím se celkovém průtoku směsi výparníkem lze dosáhnout více způsoby. Lze použít automaticky pracující armatury využívající snímání změn tlaků. Použití těchto armatur je však technicky i z hlediska pořizovacích nákladů v porovnání s armaturami se pevným nastavením náročnější a může se vyplatit spíše u rozsáhlejších akcí. Pro použití se nabízí:
- samočinně pracující regulační armatury využívajících ke svému přestavení změn tlaku
- armatury se servopohony ovládanými řídicím software
Lze však zvolit i jinou cestu, a to: společný průtok v primárním okruhu neměnit. Podle základního průtoku se nastaví pevně nastavitelné regulační armatury smyček jednotlivých vrtů a to se měnit nebude. To znamená, že celoročně bude udržován konstantní průtok nemrznoucí směsi a také stejné jímání tepla ze všech vrtů. Při nižší potřebě tepla než jmenovité bude průtok vyšší, než by byl nutný. S tím souvisí celoročně konstantní spotřeba elektrické energie na pohon oběhového čerpadla, která se nebude snižovat, pokud by postačil průtok nižší.
Je zřejmé, že uvedené možnosti dávají projektantovi možnost je posoudit a vybrat tu výhodnější.
Výše jsme hovořili o nestejně dlouhých napojeních vrtů. V principu však jde i o nestejně dlouhé smyčky zemních kolektorů, které se využívající především u rodinných domů. Proto se vždy doporučuje instalovat stejně dlouhé smyčky, aby se efekt nestejného jímání tepla ze země nemohl negativně projevit. Je vhodné doplnit, že u běžných rodinných domů není potřeba tento problém složitě řešit, protože obvykle můžeme bez problémů navrhnout smyčky primárního okruhu stejně dlouhé, ideálně z jednoho kusu potrubí bez spojů, takže nestejnoměrné zatékání do smyček nehrozí. Ale u větších aplikací vrtných polí tento fenomén existuje a je dobré o něm vědět.
Zdroje
- Čížek, P. a kolektiv – Základní vlastnosti vrtů pro tepelná čerpadla, 2012.
https://vytapeni.tzb-info.cz/tepelna-cerpadla/9245-zakladni-vlastnosti-vrtu-pro-tepelna-cerpadla - Suva® 410A Saturation Properties–Temperature Table.
https://www.cantas.com/urunpdf/20.09.008_h64423_Suva410A_thermo_prop_si.pdf
The efficiency of the heat pump also depends on the optimal design of the primary heat collector, most often in the form of a well, a surface collector, but also clinkers or energy baskets. The length of the pipe and its dimensions are closely related to the operating temperature drop in the primary circuit of the heat pump.



