Tepelné vlastnosti kotev zavěšených fasádních systémů a posouzení jejich vlivu
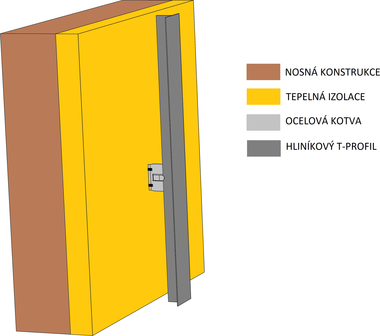
Zavěšené fasádní systémy patří ke stále častěji používaným stavebním konstrukcím. Tyto systémy je třeba připevnit k nosné konstrukci objektu pomocí kotev (obr. 1), které procházejí tepelnou izolací. Tyto kotvy způsobují v tepelné izolaci někdy i výrazné tepelné mosty. S posouzením vlivu zvolené kotvy na součinitel prostupu tepla konstrukce může pomoci tento článek.
Abstrakt
![Obr. 1 – příklad použití kotev pro zavěšené fasádní systémy [1]](/docu/clanky/0250/025001o1.jpg)
Obr. 1 – příklad použití kotev pro zavěšené fasádní systémy [1]
Článek se zabývá vlivem celokovových kotev zavěšených fasád na součinitel prostupu tepla dvouplášťových stěn. Tepelně technické vlastnosti kotev popisuje pomocí bodového činitele prostupu tepla, který lze získat pomocí odvozeného vzorce nebo výpočetní pomůcky.
Data pro odvození vzorce a výpočetní pomůcky byla získána pomocí trojrozměrného modelování a analýzy vypočtených dat v rámci diplomové práce [2]. Vstupní údaje a potřebné podklady použité pro výpočet byly poskytnuty firmou H&B delta. Článek tedy poskytuje možnost jednoduchého výpočtu a případného porovnání několika materiálových a konstrukčních variant používaných celokovových kotev.
Kotvy v zavěšených fasádních systémech
Kotev pro zavěšené fasádní systémy existuje mnoho variant. Od různých materiálových řešení po různá řešení tvaru. Většinou se používají kotvy celokovové (nejčastěji z ocelových nebo hliníkových slitin), k dispozici jsou však také kotvy s přerušeným tepelným mostem [3].
Vliv kotev zavěšených fasádních systémů na prostup tepla obvodovou stěnou se v praxi občas zohledňuje jen orientačně s pomocí přirážky k součiniteli tepelné vodivosti (λ) tepelné izolace, skrz kterou kotvy prostupují. Tato přirážka se obvykle uvažuje od 5 % do 15 % [4]. Jde ale pouze o hrubý odhad, skutečný vliv kotev může být i značně vyšší.
Pro přesnější výpočty součinitele prostupu tepla stěny se zavěšeným fasádním obkladem je proto třeba vždy stanovit tzv. bodový činitel prostupu tepla, který vyjadřuje přesně měrný tepelný tok prostupem kotvou. Pomocí tohoto činitele (označovaného jako χ a udávaného ve W/K) lze také mezi sebou snadno porovnávat jednotlivé řešení kotev.
Tento článek přináší výsledky podrobné 3D analýzy různých celokovových kotev právě s ohledem na jejich výsledný bodový činitel prostupu tepla.
Výpočet 3D vedení tepla v programu Comsol Multiphysics
Obr. 2 – Trojrozměrný model použité kotvy a podložky od firmy H&B delta
Postup výpočtu bodového činitele prostupu tepla uvádí norma ČSN EN ISO 10211 [5]. Uvedená metodika byla použita pro stanovení tepelných parametrů celokovových kotev firmy H&B delta [1]. Pro výpočet trojrozměrného stacionárního teplotního pole v kotvě a jejím okolí byl využit program Comsol Multiphysics 4.2 [6]. Trojrozměrný model kotvy a podložky použitý ve výpočtu je zobrazen na obr. 2.
Trojrozměrný model tepelného mostu a výpočet bodového činitele prostupu tepla
Obr. 3 – Použitý 3D model pro výpočet variant
Ve výpočtu byly hodnoceny tři základní materiálové varianty kotvy: nerezová, ocelová a hliníková. Pro každou variantu kotvy byly uvažovány různé tepelné odpory podkladní nosné konstrukce, a to od 0,1 do 5 m2K/W (0,1; 0,25; 0,4; 0,75; 1; 1,5; 2; 3 a 5). Důležitou vlastností je i tloušťka tepelné izolace a její součinitel tepelné vodivosti. I zde byla zvolena škála běžně používaných tlouštěk tepelné izolace (50, 60, 80, …, 200 mm). Dále byl posuzován vliv podložky, její absence nebo naopak přidání druhé podložky pod kotvu. Do výpočetního modelu kotvy byl zahrnut i nosný T profil obkladu fasády. Samotný obklad nebyl ve výpočetním modelu uvažován, protože bylo v rámci přípravných analýz ověřeno, že je jeho vliv na výsledný bodový činitel prostupu tepla kotvy zanedbatelný.
Model použitý pro výpočet variant měl několik částí (viz obr. 3). Neměnnou částí byl model nosné konstrukce (na obrázku červeně). Měnila se délka kotvy (zeleně), tloušťka tepelné izolace (modře) a počet podložek. Těchto konstrukčních variant bylo celkem 48. Po vynásobení materiálovými variantami bylo vypočteno celkově 2592 jednotlivých variant. Podrobnější popis modelu a postupu výpočtu je uveden v diplomové práci [6].
Zpracování vypočtených výsledků
Cílem prezentované analýzy nebyl jen výpočet přesných hodnot bodových činitelů prostupu tepla různých variant kotev z 3D výpočetních modelů, ale i zpracování výpočetní pomůcky a vztahu pro rychlý orientační výpočet.
Jak výpočetní pomůcka, tak vztah pro orientační výpočet umožňují určit bodový činitel prostupu tepla určité kotvy umístěné na stěně se známým tepelným odporem a známou tloušťkou tepelné izolace, aniž by bylo nutné vytvářet 3D model a počítat trojrozměrné teplotní pole.
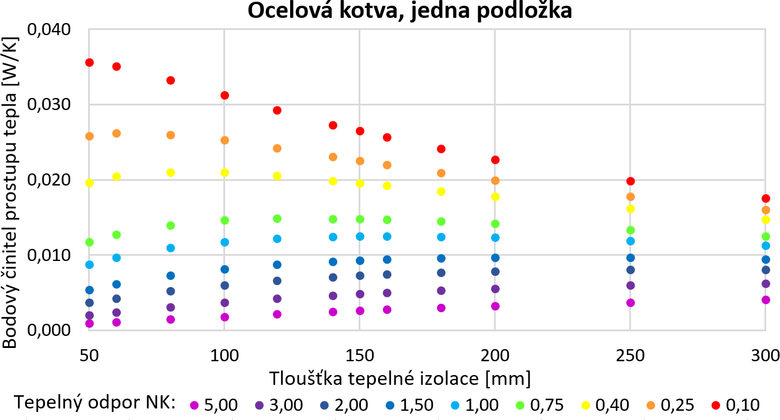
Pro odvození potřebných vztahů byl použit program Matlab, v němž bylo ze všech dříve uvažovaných konstrukčních a materiálových variant zpracováno celkem 9 logických variant (nerezová, ocelová a hliníková kotva s žádnou, jednou nebo dvěma podložkami). Výsledky pro vybranou variantu (ocelová kotva s jednou podložkou) jsou zobrazeny v závislosti na tloušťce tepelné izolace na obr. 4.
Obr. 4 – Vypočtená data v programu Comsol (každý „sloupec“ dat charakterizuje konstrukční variantu)
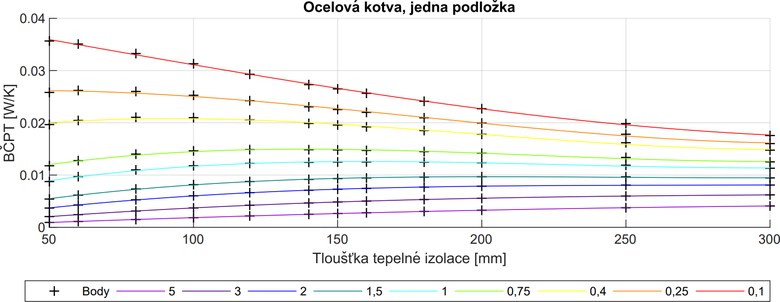
Vztahy pro přímý výpočet bodového činitele prostupu tepla pro jednotlivé varianty byly stanoveny pomocí regrese, a tedy pomocí „proložení“ vypočtených dat matematickou křivkou. Tato regrese byla vypočtena v závislosti na tloušťce tepelné izolace a v závislosti na tepelném odporu stěny (viz obr. 5).
Obr. 5 – Proložení vypočtených dat matematickými křivkami, závislost χ na tloušťce tepelné izolace
Výpočetní pomůcka „Kotva“
Obr. 6 – Výpočetní pomůcka „Kotva“
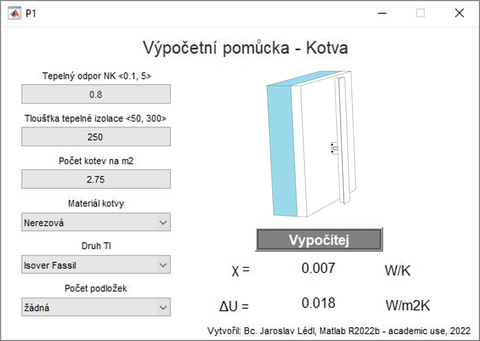
Tyto poměrně přesné matematické křivky byly použity pro odvození vzorců pro výpočetní pomůcku „Kotva“ (obr. 6), která je dostupná ke stažení na stránkách ČVUT DSpace [2].
Použití pomůcky je poměrně jednoduché. Po zvolení typu kotvy, počtu podložek, počtu podložek na m2, tepelného odporu nosné konstrukce a tloušťky tepelné izolace se po kliknutí na tlačítko „Vypočítej“ zobrazí výsledná hodnota bodového činitele prostupu tepla χ a hodnota přirážky k součiniteli prostupu tepla ΔU. Pomůcka byla vytvořena v programu Matlab.
Ve výpočetní pomůcce je možné použít tepelné odpory nosné konstrukce od 0,1 m2K/W do 5 m2K/W. Tloušťka tepelné izolace zadaná o výpočetní pomůcky se musí pohybovat od 50 mm do 300 mm. Typ použité tepelné izolace může být Isover Uni, Isover Fassil nebo izolace se stejným součinitelem tepelné vodivosti jako mají tyto dvě tepelné izolace.
Vztahy pro orientační výpočet bodového činitele prostupu tepla
Kromě výpočetní pomůcky „Kotva“ byl odvozen i vzorec vhodný pro rychlý orientační výpočet. Pro tento vzorec byly z důvodu zjednodušení použity méně přesné funkce o nižších mocninách. Toto zjednodušení má vliv na přesnost výpočtu zejména u vysokých hodnot bodového činitele prostupu tepla a při kombinaci nízkého tepelného odporu nosné konstrukce a 300 mm tloušťky tepelné izolace. Pro přesnější výpočet je tedy vždy lepší použít výpočetní pomůcku.
Orientační hodnotu bodového činitele prostupu tepla lze stanovit ze vztahu:
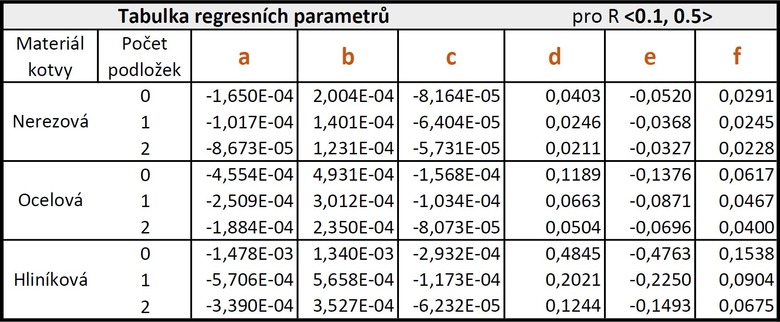
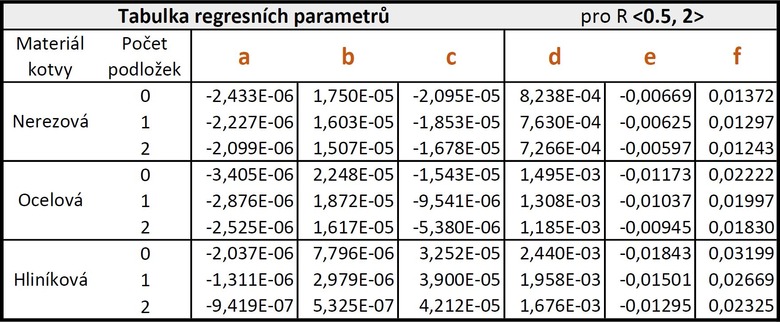
kde χ je bodový činitel prostupu tepla ve W/K, R je tepelný odpor nosné konstrukce v m2K/W, dTI je tloušťka tepelné izolace v mm a konstanty a až f jsou regresní parametry uvedené v tab. 1 a tab. 2.
Tab. 1 – regresní parametry pro R mezi 0,1 a 0,5 m2K/W
Tab. 2 – regresní parametry pro R mezi 0,5 a 2 m2K/W
Výše uvedený vztah lze použít pro tepelné odpory nosné konstrukce od 0,1 m2K/W do 2 m2K/W. Tloušťka tepelné izolace zadaná do vztahu se musí pohybovat od 80 mm do 300 mm. Typ použité tepelné izolace je Isover Uni s návrhovým součinitelem tepelné vodivosti λu = 0,038 W/mK.
Výsledný vliv bodových kotev na součinitel prostupu tepla obvodové stěny vyjadřuje přirážka k součiniteli prostupu tepla:
kde n je počet kotev na m2 (1/m2) a χ je bodový činitel prostupu tepla ve W/K.
Porovnání přesnosti výpočtu vztahem a výpočetní pomůckou
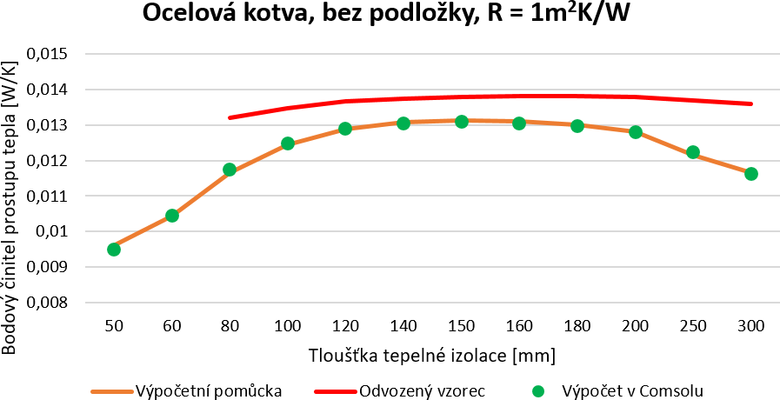
Na závěr se podívejme ještě na porovnání přesnosti výpočtu bodového činitele prostupu tepla s pomocí výpočetní pomůcky „Kotva“ a s pomocí vztahu pro orientační výpočet.
Pro porovnání byla zvolena ocelová kotva bez podložky (obr. 7). Zelenými body jsou na grafu zobrazeny přesné výsledky z programu Comsol. Oranžovou křivkou jsou zobrazeny výsledky z výpočetní pomůcky „Kotva“. Z grafu je vidět, že jsou velmi přesné. Červená křivka označuje výsledky získané pomocí vztahu pro orientační výpočet. Zde je již odchylka výraznější, nicméně ve všech případech jde o posun na stranu bezpečnosti, což je plně v souladu s tím, jak byl vztah odvozen a zkalibrován.
Obr. 7 – Porovnání přesnosti výpočetní pomůcky a vztahu pro orientační výpočet
Výpočetní pomůcku „Kotva“ lze tedy doporučit pro získání víceméně přesných hodnot bodových činitelů prostupu tepla kotev. Vztah pro orientační výpočet je vhodný spíše pro bezpečný odhad vlivu kotev.
Literatura
- Poskytnuté obrázky od hbdelta.cz – H&B delta – střechy a stavby, odvětrávané fasády, výroba z plechu. hbdelta.cz [online]. 2022 [cit. 05.12.2022]. Dostupné z: https://hbdelta.cz/
- Lédl, Jaroslav. Analýza vlivu kovových kotev fasádních obkladů na šíření tepla. Praha: Diplomová práce. ČVUT v Praze, Fakulta stavební, Katedra konstrukcí pozemních staveb. Vedoucí práce doc. Dr. Ing. Zbyněk Svoboda., 2023.
- Let, Martin. Zjednodušené stanovení bodového činitele prostupu tepla kotev s přerušeným tepelným mostem. TZB-info. [Online] https://stavba.tzb-info.cz/prostup-tepla-stavebni-konstrukci/22198-zjednodusene-stanoveni-bodoveho-cinitele-prostupu-tepla-kotev-s-prerusenym-tepelnym-mostem, 2021.
- Svoboda, Zbyněk. Tepelné efekty bodových kotev zavěšených fasádních obkladů. TZB-info. [Online] https://stavba.tzb-info.cz/prostup-tepla-stavebni-konstrukci/4737-tepelne-efekty-bodovych-kotev-zavesenych-fasadnich-obkladu, 2008.
- ČSN EN ISO 10211 Tepelné mosty ve stavebních konstrukcích – Tepelné toky a povrchové teploty – Podrobné výpočty, ČAS 2017.
- COMSOL, Multiphysics 4.2., https://www.comsol.com, Stockholm, Švédsko: COMSOL AB, 2011.
The paper deals with the effect of all-metal anchors of suspended facades on the heat transfer coefficient of double skin walls. The thermal properties of the anchors are described by means of the point heat transfer coefficient, which can be obtained using a derived formula or calculation aid.
The data for the derivation of the formula and the calculation aid were obtained by three-dimensional modelling and analysis of the calculated data in the framework of the thesis [2]. The input data and the necessary documents used for the calculation were provided by H&B delta. The thesis thus provides a simple calculation and possible comparison of several material and design variants of the used all-metal anchors.