Setrvačnost náběhu a chladnutí otopných těles
Inertia of Start Up and Cooling of Radiators
Motivací k výzkumu setrvačností náběhu a chladnutí otopných těles (OT) je aktuální všeobecné úsilí o dosahování energetických úspor a optimalizaci technických systémů, otopné nevyjímaje. Ve fázi návrhu se ve stále větší míře uplatňuje počítačové modelování, za provozu pak přichází ke slovu regulace a automatické řízení, přičemž všechny tyto obory spolu úzce souvisí. Pro efektivní regulaci systému je velmi důležitá znalost časových konstant (u otopných těles nazývaných setrvačností) jednotlivých prvků.
Motivací k výzkumu setrvačností náběhu a chladnutí otopných těles (OT) je aktuální všeobecné úsilí o dosahování energetických úspor a optimalizaci technických systémů, otopné nevyjímaje. Ve fázi návrhu se ve stále větší míře uplatňuje počítačové modelování, za provozu pak přichází ke slovu regulace a automatické řízení, přičemž všechny tyto obory spolu úzce souvisí. Pro efektivní regulaci systému je velmi důležitá znalost časových konstant (u otopných těles nazývaných setrvačností) jednotlivých prvků.
Stanovení setrvačnosti náběhu a chladnutí pro otopná tělesa je poněkud problematické vzhledem k praktické obtížnosti korektního stanovení časového průběhu střední povrchové teploty tm, což je zřejmě důvodem relativně nízkého stupně propracovanosti daného tématu ve srovnání s jinými oblastmi oboru vytápění. V minulosti byla k danému účelu používána dotyková teplotní čida, viz např. [4] a [10]. Rozvoj bezkontaktního snímání teplot termovizní technikou přinesl zcela nové možnosti pro sledování procesů chladnutí a náběhu (obr. 1) i pro stanovení časového průběhu střední povrchové teploty otopného tělesa.
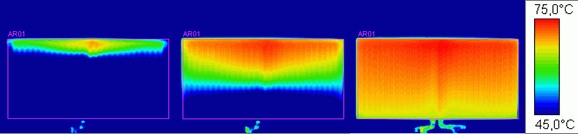
Obr. 1 Ukázka termovizního záznamu náběhu OT MM 10 - 500 x 1000 [9]
EXPERIMENTÁLNÍ MĚŘENÍ
Experimenty probíhaly v laboratořích Ústavu techniky prostředí FS ČVUT v Praze. Jako základní měřicí nástroj sloužila termovizní kamera ThermaCAM S65, důležitou roli hrál i zdroj tepla vlastní konstrukce, chráněný průmyslovým vzorem, jenž je schopen udržovat zvolenou teplotu vstupní otopné vody (75 °C při provedených měřeních) v rozmezí ± 0,1 °C. Pro správné vyhodnocení získaných termovizních snímků (více viz [3]) byly sledovány i teplota a relativní vlhkost vzduchu ti resp. φi, dále emisivita povrchu tělesa ε, následovalo měření výsledné teploty tg, objemového průtoku ![]() a teplot otopné vody na vstupu (twin) a výstupu (twout) otopného tělesa. Na základě příslušných parametrů byl přepočten výkon tělesa [1] a z výsledných charakteristik byly odečteny hodnoty T63N a T63CH. Podrobný popis experimentu viz [9].
a teplot otopné vody na vstupu (twin) a výstupu (twout) otopného tělesa. Na základě příslušných parametrů byl přepočten výkon tělesa [1] a z výsledných charakteristik byly odečteny hodnoty T63N a T63CH. Podrobný popis experimentu viz [9].
STŘEDNÍ POVRCHOVÁ TEPLOTA
Setrvačnosti náběhu (T63N) i chladnutí (T63CH) jsou odvozovány z časového průběhu poměrného výkonu otopného tělesa, jehož výpočet vychází ze znalosti průběhu střední povrchové teploty v čase. Její stanovení bylo v minulosti vzhledem k dostupné technice odkázáno na měření v několika málo bodech. Např. v [10] konkrétně ve třech, a to v blízkosti vstupu a výstupu otopné vody a uprostřed plochy tělesa. V [4] se vycházelo z teplot otopné vody před a za tělesem. Termovizní kamera a její programové vybavení umožňuje stanovení střední teploty pro libovolnou oblast zprůměrňováním změřených hodnot na jednotlivých pixelech snímače. Porovnání časových průběhů povrchových teplot při náběhu, získaných pro různý počet bodů a pro celou plochu otopného tělesa je na obr. 2. Schéma rozmístění tří a devíti bodů na ploše tělesa je na obr. 3.
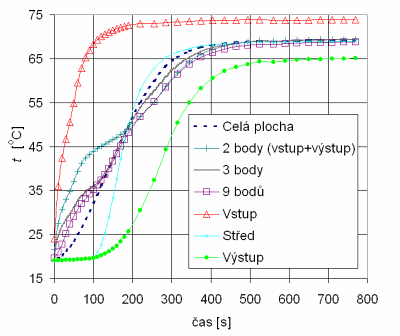
Obr. 2 Porovnání časových průběhů povrchových teplot pro různý počet a umístění
měřicích bodů při náběhu OT KL 10 - 500 x 1000, napojení oboustranné shora dolů
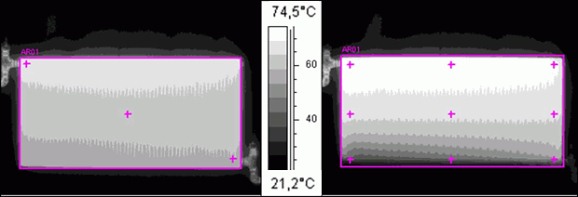
Obr. 3 Schéma umístění měřicích bodů na OT KL 10 - 500 x 1000, vlevo chladnutí, vpravo náběh
Na základě uvedených grafů lze konstatovat, že měření střední povrchové teploty otopných těles termovizní kamerou po celé ploše tělesa má zásadní význam pro korektní analýzu tepelné setrvačnosti u náběhu. Jak dokazuje obr. 2, ani měření v devíti bodech nezajistí dostatečnou přesnost získané charakteristiky ve srovnání s průběhem tm měřeným pro celou plochu tělesa. Maximální relativní odchylka činí až 30 %. Odečet parametrů důležitých pro stanovení setrvačnosti náběhu (inflexní bod a směrnice tečny) je vzhledem k nerovnoměrnému průběhu problematický a případné takto získané výsledky značně diskutabilní. Naproti tomu pro chladnutí tělesa je teoreticky možno bodové měření střední povrchové teploty připustit. Dosahovaná max. relativní odchylka průměru ze tří bodů činí méně než 5 % a pro bod ve středu tělesa dokonce méně než 2 %.
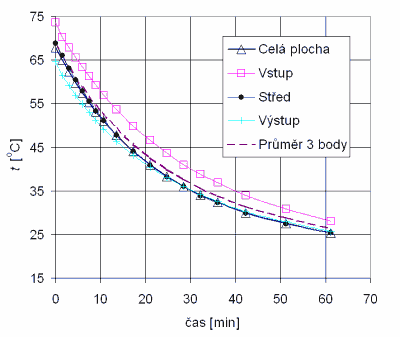
Obr. 4 Porovnání časových průběhů povrchových teplot pro různý počet a umístění měřicích
bodů při chladnutí OT KL 10 - 500 x 1000, napojení oboustranné shora dolů
ZÁKLADNÍ POPIS SYSTÉMU
Poměrně zevrubný teoretický rozbor lze nalézt v [9]. Základní schéma zkoumaného případu je na obr. 5 doplněné o rovnici (1) popisující energetickou bilanci.

Obr. 5 Energetická bilance otopného tělesa
![]()
kde α - součinitel přestupu tepla [W.m-2.K-1] |
Indexy: c - celkový |
| mT = 10,41 kg | cT = 480 J.kg-1.K-1 |
| mW = 2,7 kg | cw = 4186 J.kg-1.K-1 |
| ST = 1,128 m2 | φ = 1 |
| ε = 0,92 | σ = 5,67.10-8 W.m-2.K-4 |
Tab. 1 Parametry zkoumaného deskového OT MM 10 - 500 x 1000 [6]
a materiálové konstanty
PROCES CHLADNUTÍ
Chladnutí tělesa předchází jeho provoz v ustáleném stavu, po uzavření připojovacích armatur pak dochází k vyrovnání teplot jeho povrchu, vodního obsahu a materiálu pláště na teplotu okolí. Výsledná setrvačnost chladnutí T63CH pro ocelové deskové těleso MM 10 - 500 x 1000 vychází 1580 s. Tato hodnota byla stanovena graficko-početní metodou z průběhu poměrného výkonu OT přepočteného na nominální podmínky [9]. Vyjadřuje dobu, za kterou se poměrný výkon tělesa sníží o 63,2 %, tzn. jedná se o časovou konstantu systému 1. řádu (více[12]), taktéž definuje směrnici tečny v počátečním bodě. Pro hlubší prostudování zkoumaných procesů byla provedena simulace v programu Matlab/Simulink [5] a schéma je uvedeno na obr. 6. Chladnutí otopného tělesa bylo popsáno diferenciální rovnicí, vycházející z celkové bilance (1):
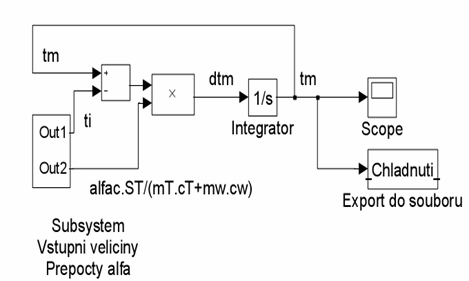
Obr. 6 Schéma modelu chladnutí OT v programu Matlab/Simulink
![]()
Výpočet celkového součinitele přestupu tepla αC (konvekcí a radiací) vychází z [1] podrobnosti viz [5]. Rovnice (2) má analytické řešení (3), jež je možno využít např. k ověření výsledků výpočtu numerickými metodami. V tomto případě byl využit tabulkový procesor Excel. Časová konstanta T0 je definována rovnicí (4) nebo lze dosadit naměřenou hodnotu T63CH [9]
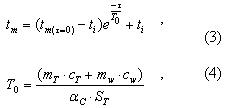
T0 časová konstanta [s].
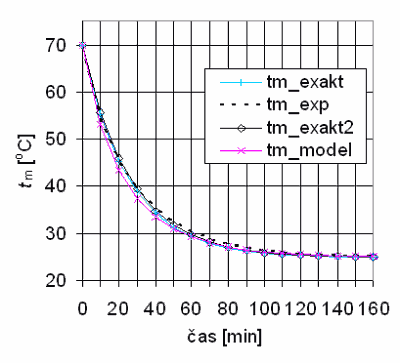
Obr. 7 Časový průběh tm analytického řešení s vypočítanou (exakt) a změřenou (exakt2) setrvačností
chladnutí, modelu a experimentální výsledky (exp) pro těleso MM 10 - 500 x 1000
Získané výsledky simulace souhlasí s experimentálními daty pro otopné těleso MM 10 - 500 x 1000 (obr. 7) s max. relativní odchylkou 6,6 %. Nejlepšího výsledku (max. rel. odchylka 2,8 %) dosáhl výpočet analytického řešení s experimentálně zjištěnou setrvačností chladnutí T63CH = 1580 s, což umožňuje výpočet průběhu chladnutí otopného tělesa i v jednoduchých tabulkových procesorech. Tím je zároveň potvrzena důležitost experimentálního stanovení setrvačnosti chladnutí T63CH u jednotlivých druhů a typů otopných těles.
PROCES NÁBĚHU
Náběh otopného tělesa představuje mnohem složitější proces než chladnutí, po otevření připojovacích armatur dochází k vytlačování původního vodního obsahu o teplotě okolí přívodní otopnou vodou. V rovnici (1) se tak některé konstanty stávají proměnnými. V první řadě se jedná o plochu tělesa ST sdílející teplo, k přestupu tepla dochází jen z plochy s vyšší povrchovou teplotou než je teplota okolí. Proměnnou a neznámou je v počáteční fázi náběhu též výstupní teplota vody twout, jelikož vstupní voda je ve styku s původní náplní o teplotě okolí a ochlazuje se pravděpodobně na teplotu nižší než za ustálených provozních podmínek. Při experimentálním stanovení setrvačnosti náběhu je nutno vzít v úvahu skutečnost, že dle tvaru výsledné přechodové charakteristiky (obr. 8) se jedná o proces vyššího než 1. řádu, čemuž je nutno přizpůsobit grafický odečet časové konstanty, resp. setrvačnosti náběhu T63N (metodika např. [7]). Pro daný případ byla zvolena metoda inflexního bodu a sečny. Výsledná hodnota takto získané setrvačnosti náběhu T63N činí 85 s, dopravní zpoždění TD = 100 s.
Použití programu Matlab/Simulink umožňuje relativně snadné zadání a výpočet diferenciální rovnice (1) i s proměnnými parametry popsanými výše bez nutnosti hledání analytického řešení. Nicméně výsledky získané z takto sestaveného modelu se značně rozcházejí s experimentálními daty a relativní odchylka časového průběhu teploty tm činí až 30 %. Ani přidání proměnných parametrů ST a twout netvoří diferenciální rovnici druhého příp. vyššího řádu, jak by odpovídalo změřené přechodové charakteristice.
Pro účely modelování časového průběhu tm a potažmo výkonu tělesa byla dále vyzkoušena metoda vycházející ze statistické analýzy naměřených dat. V programu LAB Fit se metodou nejmenších čtverců odvodila charakteristická rovnice (5) a její koeficienty, jež nejlépe aproximují změřený průběh tm. Srovnání s experimentálními daty poskytuje obr. 8 a max. relativní odchylka činí 2,4 %.
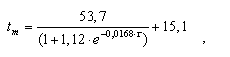 (5)
(5)
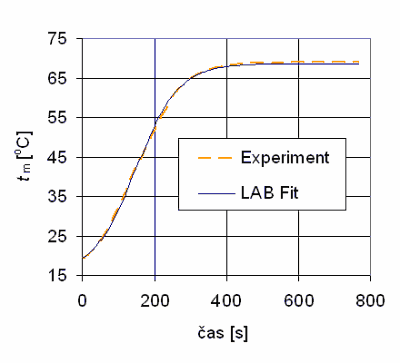
Obr. 8 Srovnání experimentálně zjištěného průběhu tm pro OT MM 10 - 500 x 1000
a statistické aproximace
ZÁVĚR
Experimenty prokázaly použitelnost metody termovizního snímání povrchové teploty pro určování tepelné setrvačnosti náběhu a chladnutí pro desková otopná tělesa. Ze srovnání průběhů povrchových teplot pro různý počet bodů na tělese vyplývá, že pro korektní stanovení tepelné setrvačnosti zejména náběhu má zásadní význam snímání povrchové teploty na celé ploše tělesa. Pro výpočet tm z devíti povrchových bodů otopného tělesa činí maximální relativní odchylka od průběhu stanoveného pro celou plochu až 30 %. U chladnutí je situace příznivější, maximální hodnota relativní odchylky časové charakteristiky tm získané ze tří bodů se pohybuje pod 5 %.
Stanovení setrvačnosti chladnutí T63CH ze změřených přechodových charakteristik poměrného výkonu OT přepočteného na jmenovité podmínky se řídí metodikou pro soustavy 1. řádu [9], [12]. Modely chladnutí vycházející ze základní energetické bilance (1) vykazují dobrou shodu s experimentálními daty. Simulace v prostředí Matlab/Simulink dosahuje maximální relativní odchylky 6,6 %, výpočet analytického řešení (3) v Excelu za použití experimentálně získané setrvačnosti chladnutí T63CH = 1580 s dokonce pouze 2,8 %. Výpočet bez nutnosti numerického řešení diferenciální rovnice je zajisté velkou výhodou.
Proces náběhu představuje komplikovaný proces a zjednodušený přístup k simulaci založený na základní bilanční rovnici (1) nevedl k dobrým výsledkům. Vypočtený průběh se lišil o více než 30 %, a to i při uvažování časově proměnných hodnot plochy sdílející teplo a výstupní teploty otopné vody. Důvodem je mj. fakt, že experimentálně stanovená přechodová charakteristika odpovídá systému 2. a vyššího řádu, kdežto rovnice (1) je pouze 1. řádu. Řešením může být např. statistická aproximace změřeného průběhu, prezentovaná v rovnici (5). K odečtu příslušné hodnoty setrvačnosti náběhu T63N pro využití v oblasti měření a regulace bylo použito metody sečny a inflexního bodu [7]. Výsledné hodnoty vycházejí takto: T63N = 85 s a TD = 100 s.
Použité zdroje:
[1] Bašta, J. Otopné plochy. Praha: vydavatelství ČVUT, 2001, 328 s., ISBN 80-01-02365-6.
[2] Bašta, J., Šimek, J., Vavřička, R. Dynamické chování deskových otopných těles. Vytápění, větrání, instalace, 2008, roč. 17, č. 3, s. 129 - 134
[3] FLIR Systems. ThermaCAM Researcher : User's manual. Rev. a74, 2004. 146 s.
[4] Ham, Ph. J. Dynamisch warmtegedrag van radiatoren en convectoren: Metingen en modelvorming. Verwarming en Ventilatie. 1988, no. 5, s. 315 - 333
[5] Jančík, L., Bašta, J. Posouzení dynamického chování otopných těles termografickou metodou. In: 5. Konference simulace budov a techniky prostředí SBTP '08, Brno, 2008, s. 45 - 49, ISBN 978-80-254-3373-7
[6] Korado a.s., Česká Třebová. Informace o výrobcích [online]. Dostupné z WWW.
[7] Noskievič, P. Modelování a identifikace systémů / 1. vyd. Ostrava : Montanex, 1999, 276 s., ISBN 80-7225-030-2.
[8] Silva, Wilton P. and Silva, Cleide M. D. P. S., LAB Fit Curve Fitting Software: (Nonlinear Regression and Treatment of Data Program) V 7.2.44 [online]. 1999-2009 [cit. 2009-02-13]. Dostupné z WWW.
[9] Šimek, J. Dynamické chování otopných těles. Praha: ČVUT, 2008, 110 s. [Diplomová práce 35-TŽP 2008]
[10] Výzkumný ústav pozemních staveb. Tepelná setrvačnost otopných těles z hlediska regulace. Výzkumná zpráva. Praha: Výzkumný ústav pozemních staveb, 1987, 20 s.
[11] Zítek, P. Matematické a simulační modely / 1. vyd. Praha: ČVUT, 1996, 128 s, ISBN 80-01-01524-6.
[12] Zítek, P. Základy automatického řízení. Praha: vydavatelství ČVUT, 1993, 147 s, ISBN 80-01-01016-3.
Recenze - prof. Ing. Karel Hemzal
Autoři představují novou metodu stanovení tepelných setrvačností náběhu T63N a chladnutí T63CH deskových otopných těles založené na termovizním snímání povrchové teploty. Stručný popis experimentu je doplněn rozborem stanovení reprezentativní hodnoty střední povrchové teploty, problematikou určování T63N a T63CH a stručným popisem modelů v prostředí Matlab/Simulink a Excel. Ze získaných výsledků vyplývá použitelnost termovizního snímání k danému úkolu a nutnost sledovat průběh povrchové teploty tělesa v celé ploše zejména u náběhu. Chladnutí tělesa odpovídá chování systému 1. řádu, kdežto charakteristika náběhu systému min. 2. řádu, což je nutno zohlednit jak při stanovování příslušných setrvačností tak při simulacích. Model chladnutí vycházející z energetické bilance vykazuje dobrou shodu s experimentem (max. relativní odchylka do 6 %), výpočet z analytického řešení dokonce do 3 %. K modelování náběhu bylo využito statistické analýzy změřených dat.
Authors present a new method for determination of thermal inertia of start-up T63N and cooling T63CH of panel radiators based upon the thermo-vision recording of the surface temperature. A brief description of the experiment is supplemented with the analysis of determination of a presentable value of the mean surface temperature, problems of the T63N and T63CH determination and the brief description of models in the environment Matlab/Simulink and Excel. The provided results result in the usability of the thermo-vision recording with respect to the specified task and the necessity of monitoring the course of the radiator surface temperature in its entire surface, particularly at the start-up. The radiator cooling corresponds to the behavior of the 1st range system while the characteristics of the start-up minimally to the 2nd range, which has to be reflected both in the determination of relevant inertias and simulations. The model of cooling, which ensues from the energy balance is showing a good concord with the experiment (max. relative deviation up to 6 %), the calculation ensuing from the analytic solution only up to 3 %. The statistical analysis of the measured data was used for modeling the start-up.