Lanové sítě pro skleněné fasády – Úvodní studie
Článek uvádí úvodní informace k návrhu předpjatých lanových sítí podpírajících rozměrné skleněné fasády. Popsány jsou jednotlivé fasádní prvky a příklady významných realizovaných fasád. V přehledu primárních publikací je ukázán vývoj experimentálních a teoretických přístupů k řešení problémů spojených s návrhem těchto konstrukcí (zajištění potřebné tuhosti a únosnosti, rizika spojená se selháním spojení skleněných tabulí s lanovou sítí, kolapsem kotev či ztrátou předpětí lan, dynamické chování při poruchách, výbuších a zemětřesení, vlivy teploty). Podrobněji jsou popsány práce použité v navazující části [31] pro validaci a verifikaci vlastního numerického řešení a parametrické studie těchto fasád.
1. Úvod
1.1 Obecně
Fasády dominantních budov a hal vždy zaznamenávaly trendy a pokrok nejen v architektuře, ale i ve stavebnictví jako celku. Významným přechodem od různých silikátových plášťů a později kovoplastických sendvičů to byly luxusní kamenné obklady, avšak v posledních desetiletích převládají skleněné fasády nejrůznějších forem.

Obr. 1 Podepření skleněnými stěnami (hotel Sheraton Mirage Austrálie), podepření rámovou konstrukcí (Strongback glass facade) s lokálními bodovými držáky, podepření vodorovným předpjatým lanovým nosníkem (hala letiště Singapore)
Nosný systém skleněných fasád, zejména pro přenos účinků tlaku/sání větru a zajištění dostatečné tuhosti pro akceptovatelný průhyb, se vyvíjel od liniových rámových konstrukcí (sloupků a příčlí) k transparentnějším konstrukcím, jako jsou skleněné podpůrné stěny a lokální podpory skleněných tabulí. Výrazný pokrok poté přinesly lanové prvky, zprvu ve formě lanových předpjatých nosníků (ve svislém nebo vodorovném směru), obr. 1. Zásadní změnu však přineslo použití předpjatých lanových sítí, které přinášejí další otevření prostoru, transparentnost, efektivitu z hlediska nosné konstrukce i vytváření tvarových možnosti z hlediska architektury.
Předpjaté lanové sítě mohou být jednosměrné (s lany buď ve svislém nebo vodorovném směru) nebo dvojsměrné (s ortogonálním uspořádáním lan), a to rovinné i zakřivené (antiklastické, dvojité křivosti), obr. 2. Kotvení předpínacích lan může být tuhé nebo pružné (pérové), umožňující stimulaci síly při případném výrazném dynamickém zatížení. Z výzkumu Yussofa [1] a autorů [2] plyne, že zakřivené sítě jsou tužší a vyžadují menší předpínací síly, avšak musejí zajistit dostatečné předpětí pro oba směry větru.

Obr. 2 Jednosměrná svislá síť (Lufthansa Aviation Centre Frankfurt, 2006), dvojsměrná rovinná lanová síť (Market Hall Rotterdam, 2014), dvojsměrná zakřivená lanová síť (Sea-Tac International Airport Seattle, 2005)
Lanové sítě mohou pokrývat rozměry fasád v mnoha desítkách metrů (např. New Poly Plaza v Pekingu má rozměr 90×60 [m], Hilton hotel v Mnichově 25×40 [m] a letiště v Malaze 900×24÷12 [m], obr. 3). Typické rozměry čtvercových skleněných tabulí u lanových sítí jsou do 1,5 m, popř. u obdélníkových tabulí do 2,1×2,4 [m] a nedosahují tedy dostupných možností výroby skel (až 3,21×6 [m]). Lana jsou obvykle jednopramenné konstrukce z nerezové oceli, s průměrem 19÷36 mm.
Obr. 3 New Poly Plaza v Pekingu (2007), Hilton (Kempinski) hotel v Mnichově (1993), Letiště v Malaze (2010)
Skleněné tabule ve fasádách jsou vesměs z vrstveného (laminovaného) tepelně zpevněného, popř. tepelně tvrzeného bezpečnostního skla. Viskoelastické mezivrstvy aplikované v autoklávech, obvykle fólie PVB (polyvinyl butyral), se aplikují v několika vrstvách tloušťky 0,38 mm. Mezeru mezi tabulemi skla zajišťuje těsnící materiál na silikonové bázi, obvykle s dvojnásobnou šířkou než je tloušťka těsnění. Pro zvýšené tepelně izolační požadavky se běžně u těchto lanových sítí aplikují izolační dvoj- a více- skla s mezerou vyplněnou netečným plynem nebo vysušeným vzduchem, osazovaná do nerezových rámečků. Další podrobnosti rozebírá vhodně Pešek [3]. Skleněné tabule se připojují k lanové síti bodovými držáky, principiálně dvěma způsoby: svorkou, nebo šroubovaným připojením (pavoukem), obr. 4 (pro přípoj izolačních skel lze aplikovat vložky firmy Greenlite Glass Systems - LITEWALL).

Obr. 4 Vrstvené sklo (např. 6+2×0,38+6 = 12,76 [mm]), tepelně izolační trojsklo (např. 4+14Ar+4+14Ar+4 = 40 [mm]), připojení svorkou, šroubované připojení „pavoukem“ a vložka pro izolační dvojsklo LITEWALL
Nové možnosti výroby skleněných tabulí umožňují jejich téměř libovolné zakřivení, a to nejen do válcového tvaru (jako na letišti v Seattlu, obr. 2), ale i s proměnnou křivostí, např. s vybočením do tvaru J v horní části tabule ven, jak ukazuje obr. 5 (rozměry fasády 100×22 [m]).
Držáky jsou průmyslové výrobky z nerezové austenitické oceli, obvykle čínské provenience (např. [4]). Pavouky mají 2 otvory protáhlé a dva kruhové. Kruhové zajišťují polohu pro zatížení větrem, zatímco protáhlé otvory přenášejí též vlastní tíhu zavěšených tabulí (jsou tedy v dolní poloze pavouků). Otvory mohou být u laminovaných skel skryté pouze ve vnitřní tabuli, jak naznačuje výzkum Zdražilové a Sokola [5]. Lana procházejí koncovkou držáků a finálně se zafixují po předepnutí lan, obr. 6. Relativní natočení mezi jednotlivými tabulemi skla je malé, velké je však u obvodových tabulí vůči přiléhající konstrukci, kde je nutné deformaci umožnit.
![Obr. 6a Pavouky KIN LONG a příchytka tabulí s nylonovým těsněním [4]](/docu/clanky/0260/026015o30.jpg)
![Obr. 6b Pavouky KIN LONG a příchytka tabulí s nylonovým těsněním [4]](/docu/clanky/0260/026015o31.jpg)
![Obr. 6c Pavouky KIN LONG a příchytka tabulí s nylonovým těsněním [4]](/docu/clanky/0260/026015o32.jpg)
![Obr. 6d Pavouky KIN LONG a příchytka tabulí s nylonovým těsněním [4]](/docu/clanky/0260/026015o33.jpg)
![Obr. 6e Pavouky KIN LONG a příchytka tabulí s nylonovým těsněním [4]](/docu/clanky/0260/026015o34.jpg)
Obr. 6 Pavouky KIN LONG a příchytka tabulí s nylonovým těsněním [4]
Zatímco šroubované připojení pavouky vyžaduje vrtání skleněných tabulí, svorky připojují tabule sevřením v neoprénových podložkách, s deformací danou jejich poddajností a třením, obr. 7.
![Obr. 7a Svorky KIN LONG s neoprénovými podložkami [4]](/docu/clanky/0260/026015o35.png)
![Obr. 7b Svorky KIN LONG s neoprénovými podložkami [4]](/docu/clanky/0260/026015o36.png)
![Obr. 7c Svorky KIN LONG s neoprénovými podložkami [4]](/docu/clanky/0260/026015o37.png)
![Obr. 7d Svorky KIN LONG s neoprénovými podložkami [4]](/docu/clanky/0260/026015o38.png)
![Obr. 7e Svorky KIN LONG s neoprénovými podložkami [4]](/docu/clanky/0260/026015o39.png)
Obr. 7 Svorky KIN LONG s neoprénovými podložkami [4]
Požadavky na skleněné konstrukce z hlediska mezních stavů únosnosti (MSÚ) a mezních stavů použitelnosti (MSP) jsou pro danou aplikaci dány evropskými normami [6], [7], [8]. Tyto normy umožňují stanovit potřebnou návrhovou pevnost skleněných tabulí za ohybu a příslušné omezení průhybu (popř. kmitání) při charakteristickém zatížení podle evropských norem.
Lana používaná ve fasádních lanových sítích jsou z nerezové (korozivzdorné) oceli, zejména z estetických důvodů. Vesměs se používají tvrdá otevřená jednopramenná lana 1×19, popř. dražší kompaktní (uzavřená) lana pro zvýšení pevnosti nebo lana vícepramenná (WSC – wire strand core, popř. pro zvýšenou odolnost proti teplu IWRC – independent wire rope core). Jednotlivé dráty z patentované oceli mají pevnost 1570 až 2160 MPa. Výrobci uvádějí charakteristickou pevnost při přetržení lana, z které se odvozuje návrhová únosnost v tahu lana. Předpětí lan v lanové síti vychází z výpočtů sítě pro dané zatížení (zejména větrem), aby vyhověly výsledné deformace sítě a síly v lanech. Sítě jsou vesměs ortogonální, přičemž svislá a vodorovná lana mohou mít různé parametry i předpětí (v kratším směru přebírají větší namáhání). Velikost předpětí a sil v lanech má zásadní vliv na okolní konstrukci, do které jsou lana kotvena a která musí být patřičně dimenzována. Předpětí u velkých sítí se vnáší hydraulickými napínáky na nalisované koncovce přes dočasnou matici a další maticí se fixuje. Pro omezení ovlivňování sil v lanech při předpínání je vhodné napínat více lan současně, pod jednotnou hydraulikou. Kromě pevných ukotvení jsou u rozměrných lanových sítí aplikována netuhá ukotvení pérového charakteru pro tlumení vibrací a vyrovnání sil od deformace sítě, zejména od změn teploty v době realizace a po instalaci skleněné fasády.
1.2 Publikované studie
První studie lanových sítí byly založeny na náhradě membránou (Otto, 1967 [9], Irvine, 1981 [10]) a řešení lineárních, popř. nelineárních rovnic numerickými metodami. Otázky kmitání a vlastních tvarů byly řešeny přibližnými lineárními metodami (Calladine, 1982 [11]). Realizace rozměrných předpjatých fasádních lanových sítí, počínaje dvojsměrnou sítí pro zasklení atria hotelu Kempinski, nyní Hilton (Schlaich a Bergermann, 1993 [12]) a celou řadou unikátních dvojsměrných i zakřivených lanových sítí (např. New Poly Plaza v Pekingu, 2007 [13], China Petroleum Building v Pekingu, 2007 [14], Abu Dhabi’s stock exchange, 2012 [15]) a dalších jednosměrných sítí (např. Doha Convention Center v Kataru, 2009, Sobek a kol. [16]), vedly k detailním numerickým a experimentálním studiím.
Otázky pružně deformovatelné podpůrné konstrukce lanových sítí spíše střešního charakteru řešil Talvik, 2001 [17]. Zajímavou studii ohledně technologie vnášení předpětí do lanové sítě publikovali Wang a kol., 2006 [18]. Doporučili analyzovat síť inverzně k postupu předpínání ve třech stupních a podle výsledků výpočtů předpínání realizovat, čímž omezili korekce při předpínání. Zároveň upozornili na významné zvýšení tuhosti sítě po přidání skleněných tabulí (podobné doporučení k technologii předpínání později publikovali Ming a kol. 2015 [19]). Stejní autoři vyšetřovali i dynamické chování lanových sítí, Shi a kol. 2017 [20]. Feng a kol., 2009 [21] řešili vliv skleněných tabulí na kmitání lanových sítí a jejich tlumící účinky. V následné studii Feng a kol., 2012 [22] prezentovali zjednodušené geometricky nelineární vztahy vhodné pro řešení kmitání lanových sítí, včetně odezvy na zemětřesení. Zaimovic a kol., 2015 [23] odvodili nelineární isoparametrické konečné prvky vhodné pro statické i dynamické řešení lanových sítí. Yang a kol., 2015 [24] testovali reálnou lanovou síť 4×4 z hlediska poškození. Zjistili, že ztráta spojení v uzlu lan má zanedbatelný efekt, ztráta předpětí vede ke zvýšení průhybu až o 15 %, zatímco kolaps kotvení až o 36 %, naopak tahové síly při vyřazení lana jsou ovlivněny málo. Významné disertační práce v oblasti lanových předpjatých sítí publikovali Shang, 2014 [25] a Yussof, 2015 [1], které jsou podrobně rozebrány v kapitole 2, neboť byly použity pro validaci a verifikaci výsledků v navazujícím článku [31]. Yussof a kol., 2017 [26] dále experimentálně potvrdili významné zvýšení tuhosti lanové sítě vlivem skleněných tabulí (až o 18 %) a vlivem zakřivení sítě (až o 11,5 %).
V posledním období byla publikována řada příspěvků týkající se předpjatých lanových skleněných fasád v oblasti rizikového inženýrství. Piyasena a kol., 2019 [27] porovnávají chování jednosměrných a dvojsměrných lanových sítí s chováním lanových nosníků při výbuchu. V softwaru LS DYNA je modelováno laminované sklo včetně PVB, nelineární chování lan s tlumením a pevným šroubovaným připojením skel bodovými držáky. Modelován byl výbuch 250 kg TNT ze vzdálenosti 30 m (časový profil 90 s, s maximálním tlakem 130 kPa). Zjednodušené analytické řešení účinků výbuchu publikovali Royer-Carfagni a kol., 2020 [28]. Řešení kontinua fasády je zde nahrazeno soustředěnými hmotami pod časovým zatížením podle Friedlanderova vztahu a dynamické účinky dobře vystihují chování sítě pro předběžné posouzení. Marzuki a kol., 2020 [29] testovali síť 4×4 se statickým rovnoměrným zatížením skleněných tabulí a vlastní frekvence po vypnutí některých lan s poměrně zanedbatelným vlivem, pokud bylo vypnuto pouze jedno lano. Nedávno Khalkhaliha a kol, 2022 [30] publikovali výzkum týkající se flexibilního osového uložení některých lan sítě pro optimální chování sítě při rozkmitání lan.
V této Úvodní studii jsou dále podrobněji komentovány výsledky relevantních publikovaných numerických a experimentálních studií dvojsměrných lanových sítí, na které navazuje článek Návrh a parametrické studie [31], uvádějící validaci a verifikaci numerického modelu s následnou parametrickou studií praktických předpjatých lanových sítí.
2. Vyšetřování dvojsměrných lanových sítí
2.1 Parametrická studie C. Shang
Rozsáhlou parametrickou studii publikovala Shang, 2014 [25]. Použita je geometricky nelineární pružná metoda konečných prvků bez zavedení imperfekcí (GNA) v softwaru Strand7 [32]. Numerické řešení používá Newton-Raphsonovu iteraci (N-R).
K řešení je zvolena reálná lanová síť o rozměrech 15×10 [m], s patnácti skleněnými tabulemi o rozměrech 3×1,25 [m], obr. 8.
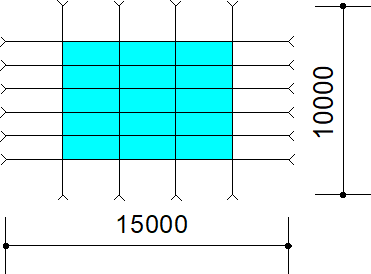
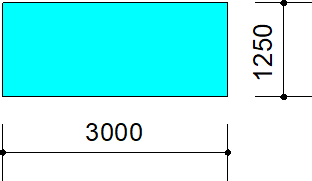
Obr. 8 Rozměry lanové sítě a rozměry vložených skleněných tabulí
Koncovky lan modelují kloubové fixní uložení v konstrukci, nastavitelné pérové uložení není zavedeno. Po zavedení předpětí a upevnění skleněných tabulí přenášejí svislá i vodorovná lana příslušné zatížení větrem, zatímco svislá lana navíc vlastní tíhu tabulí a lan. Zatížení větrem bylo uvažováno hodnotou 1 kN/m2, přičemž nebylo rozlišeno mezi charakteristickou a návrhovou hodnotou. Zatížení teplotou ani zemětřesením nebylo ve studii uvažováno.
Z hlediska dostatečné tuhosti byla zavedena limitní hodnota průhybu L/50 (L je menší rozměr sítě).
Pro zasklení bylo zvoleno tepelně zpevněné sklo tloušťky 15 mm, s limitní pevností 58 MPa a model pružnosti 70 GPa a Poissonovým součinitelem 0,21. Nerezová lana různých průměrů a konstrukcí byla limitována polovinou minimální pevnosti při přetržení (325 kN), s modulem pružnosti 130 GPa a Poissonovým součinitelem 0,28. Spojovací materiál (pavouky a svorky) počítal s modulem pružnosti 210 GPa a Poissonovým součinitelem 0,27, neoprénové podložky s modulem pružnosti 2 GPa a Poissonovým součinitelem 0,49.
Pro sklo byly použity skořepinové prvky (v místě šroubů bylo uvažováno bodové připojení), pro lana liniové prvky, pro šroubované prvky přípojů (pavouky) nosníkové prvky a pro svorky včetně neoprénových podložek objemové prvky, s uvážením kontaktů. Fixní spojení tabulí a lan bylo zavedeno pouze pro svislý směr.
Shrnutí výsledků
Studie zahrnovala danou síť s lany průřezu 22 mm, tloušťkou skla 15 mm a hodnotila limitující parametry použitých prvků pro vyhovující zatížení větrem. Průhyb dané sítě byl omezen hodnotou L/50 = 11385/50 = 227,7 mm. Předpětí lan bylo voleno jako 30 % limitní pevnosti, tj. pro lano Ø 22 mm (konstrukce 1×61) byla limitní pevnost 325/2 = 162,5 kN a předpětí ∼ 50 kN.
Numerické řešení pro spojení se svorkami vyhovělo pouze pro zatížení větrem do hodnoty 0,2 kN/m2. Průhyb uprostřed rozpětí byl přitom pouze 39 mm, síla v laně 57 kN a největší napětí ve skle 23,5 MPa. Důvodem bylo přemáhání skla v okolí svorek přenášejících dané zatížení v důsledku omezení deformací přípoje i přetížení lan. Takové spojení by vyžadovalo větší tloušťku skleněných tabulí než uvažovaných 15 mm. V tab. 1 jsou pro dvojsměrné sítě souhrnně uvedeny výsledky studie.
| Spojení | Zatížení [kPa] | Max. napětí ve skle [MPa] | Max. síla v lanech [kN] | Max. průhyb [mm] |
|---|---|---|---|---|
| svorky | 0,2 | 23,5 | 57 | 39 |
| pavouky | 1,0 | 53,3 | 101 | 209 |
Šroubované spojení (pavouky) naopak pro zatížení větrem 1,0 kN/m2 vyhovělo. Průhyb uprostřed rozpětí byl 209 mm, síla v laně 101 kN a největší lokální napětí ve skle 53,3 MPa. Nevýhodou je zde požadavek na tvrzené sklo, neboť dochází ke zvýšené koncentraci napětí v místě šroubů. Otvory mají být vyvrtané diamantovými vrtáky a následně tvrzené k odstranění vměstků sulfidu nikelnatého NiS (vyžaduje cyklus s dvouhodinovým ohřátím na 287 °C), který způsobuje lom skla. Dále se v bodových držácích striktně vyžadují protáhlé otvory umožňující vodorovný posun pro zavěšení tabule (viz kap. 1) a zvětšené otvory pro svislý i vodorovný posun v dolní části tabule v závislosti na deformacích a tepelné dilataci. Větší otvory však vyžadují dokonalé těsnění šroubů.
Studie tedy spíše upřednostňuje spojení šroubované. Nicméně realizované rozsáhlé lanové sítě se svorkami a příslušnými pružnými podložkami tyto závěry nepotvrzují a může tedy u studie Shang jít o nedokonalou detailní analýzu lokální napjatosti.
2.2 Parametrická studie M. M. Yussofa
Náročné experimentální vyšetřování publikoval Yussof, 2015 [1]. V laboratoři realizoval lanovou síť 7×7 upnutou do mohutného rámu. Síť s rozměry 305×305 [mm] tvořila lana Ø 4 mm tvořená konstrukcí 7×7 pozinkovaných drátů s pevností 1770 MPa, min. pevností při přetržení 10,2 kN, modulem pružnosti 82,85 GPa, Poissonovým součinitelem 0,3 a nalisovanou koncovkou se závitem. Vzhledem ke šroubovanému spojení v křížení jsou nosná lana o 7 mm níže než lana podporující, obr. 9. Po mechanickém předpětí pomocí klíče a kontrolovaném dynamometry byly osazeny skleněné tabule 300×300×4 [mm] bez vzájemného těsnění, s modulem pružnosti 72 GPa a připojeny dvěma destičkami 75×75×3 [mm] na pružných podložkách pomocí centrálního šroubku Ø 3 mm. Zatížení bylo aplikováno čtyřmi bodovými zatíženími pomocí mechanického nůžkového systému s dynamometrem.
Předpětí bylo aplikováno ve třech variantách (1 kN – odpovídá zhruba 10 % pevnosti při přetržení, 1,5 kN a 2,0 kN – odpovídá zhruba 20 % pevnosti při přetržení) a každé bodové zatížení včetně vlastní tíhy mechanismu F = 207,5 N (celkově 830 N).
Pro model rovinné sítě byly koncovky lan v rovině, pro dvojitě zakřivenou síť byly posunuty kolmo na srovnávací rovinu v každém směru podle obr. 10.
Kromě statických testů byly provedeny též zkoušky náhlého porušení jednoho lana a pádu ocelové kuličky Ø 60 mm (tíha 760 g) ze tří různých výšek (1,0, 1,5 a 2,0 m) na několika místech ke zjištění kmitání a vlastní frekvence lanové sítě.
Na závěr je provedena analýza v softwaru Abaqus verze 6.9, pokrývající část experimentálních výsledků (avšak pouze rovinné sítě). Numerické výsledky maximálních průhybů se téměř shodují s experimentem, s rozdílem do 1 %.
Shrnutí experimentálních výsledků
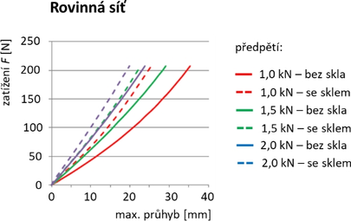
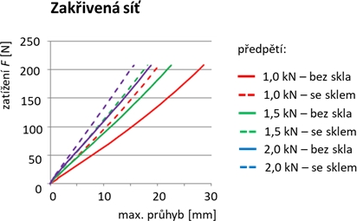
Výsledky pokrývají rovinnou i zakřivenou síť bez zasklení i se zasklením, pro všechna tři předpětí. Výraznější nelineární chování vykazovala pouze rovinná síť (a to zejména samostatná síť bez tabulí skla), zatímco zakřivená síť se při daném zatížení a všech úrovních předpětí chovala v podstatě lineárně, obr. 11.
Z výsledků je zřejmé, že zakřivená síť má výrazně menší průhyby. Toto zjištění umožňuje použít při návrhu zakřivených sítí menší předpětí, a tudíž nižší nároky na podpírající okolní konstrukce. Protože obvykle průhyby o dimenzování lanové sítě rozhodují, je toto řešení, kromě estetických předností, i ekonomičtější. Dalším zjištěním je značný vliv zasklení na zvýšení tuhosti lanové sítě, zejména u malých předpětí.
Vlivem příčného zatížení se zvyšují síly v lanové síti. Podle Tab. 2, je vliv výraznější u zakřivené sítě, kde nosná lana jsou přitěžována a podporující naopak odlehčována, přitom pro nejvyšší předpětí (2,0 kN) se přírůstek snižuje. Tabulka platí pro síť bez zasklení, při zasklení je pro rovinnou síť vliv obdobný, výraznější však pro síť zakřivenou.
| Síť | Lano uprostřed sítě | Předpětí 1,0 kN: přírůstek síly po zatížení v % | Předpětí 1,5 kN: přírůstek síly po zatížení v % | Předpětí 2,0 kN: přírůstek síly po zatížení v % |
|---|---|---|---|---|
| rovinná | nosné | +39,7 | +17,2 | +9,1 |
| podporující | +41,8 | +17,6 | +9,4 | |
| zakřivená | nosné | +66,7 | +37,7 | +24,3 |
| podporující | −30,5 | −21,3 | −14,9 |
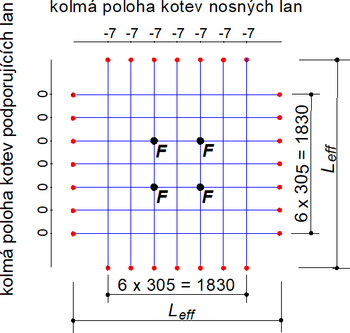
Vliv zasklení na ohybovou tuhost (průhyby) po bodovém zatížení silami F byla vyčíslena v procentech a je uvedena na obr. 12 pro rovinnou síť a na obr. 13 pro síť zakřivenou. Pro střední část sítě je vliv zasklení pro větší předpětí menší, ale pro oba případy obdobný.
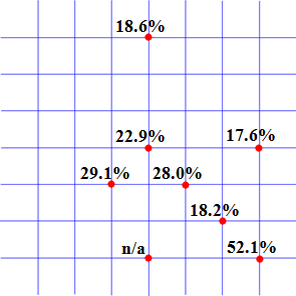
Předpětí 1 kN
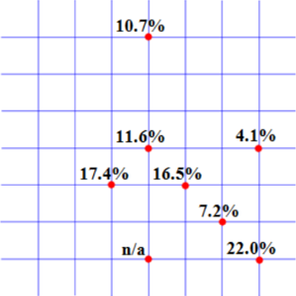
Předpětí 2 kN
Obr. 12 Rovinná síť: procentní přírůstek tuhosti vlivem zasklení
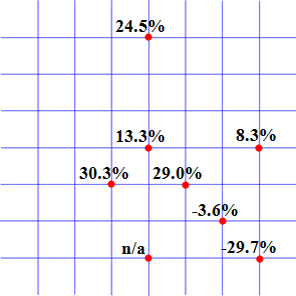
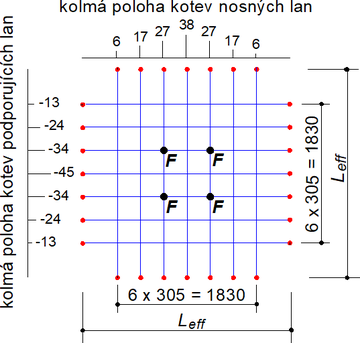
Předpětí 1 kN
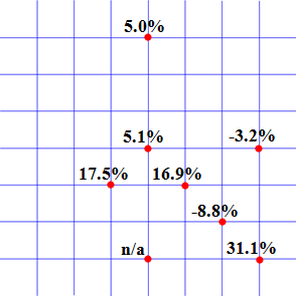
Předpětí 2 kN
Obr. 13 Zakřivená síť: procentní přírůstek tuhosti vlivem zasklení
3. Závěr
Studie podává přehled významných publikací zabývajících se předpjatými lanovými sítěmi podpírajícími rozlehlé fasádní konstrukce. Podrobně je uvedena numerická studie Shang [25] a experiment prováděný Yussofem [1], které přinesly pro návrh lanových sítí zásadní poznatky. Návrh musí respektovat podstatné vstupní parametry a podle navržené geometrie (zakřivení) zvolit optimální předpětí vedoucí po zatížení ke splnění požadované tuhosti. Současně musí respektovat nelineární chování sítě, vliv tuhosti zasklení a mezní stavy únosnosti i použitelnosti zasklení, přípojů, lan, kotvení i okolní konstrukce.
Navazující článek [31] popisuje přístup k řešení těchto konstrukcí, numerickou analýzu, její validaci a verifikaci s použitím výše uvedených zahraničních studií a parametrickou studii rovinných reálných sítí.
4. Literatura
- Yussof, M. M.: Cable-net supported glass façade systems. PhD Thesis, University of Surrey, 2015, 279 s.
- Komlev, V., Macháček, J.: Cable-net systems supporting glass facades. Proc. 27-28th Int. Conf. Eng. Mechanics 2022, Milovy, Paper #46, 2022, s. 205-208.
- Pešek, O.: Skleněné konstrukce, powerpointová prezentace. VUT Brno, 2019, 110 s.
https://www.fce.vutbr.cz/KDK/pesek.o/CO52/Prezentace_sklo_2018.pdf - Guangdong KIN LONG Hardware Products Co., Ltd. https://en.kinlong.com/Product/Point/index.html
- Zdražilová, M. and Sokol, Z.: Skrytý kotevní bod pro vrstvené skleněné konstrukce. SDZ, FSv ČVUT, 2021, 28 s.
- ČSN EN 16612 Sklo ve stavebnictví – Stanovení únosnosti příčně zatížených tabulí skla výpočtem. ÚNMZ, 2021, 44 s.
- CEN/TS 19100-1 Design of glass structures - Part 1: Basis of design and materials. EN-CENELEC, 2021, 44 s.
- CEN/TS 19100-2 Design of glass structures - Part 2: Design of out-of-plane loaded glass components. EN-CENELEC, 2021, 35 s.
- Otto, F: Tensile structures, MIT Press, Vols 1 and 2, Cambridge, 1967, 171 a 320 s.
- Irvin, H. M.: Cable structures. MIT Press, 1981, 259 s.
- Calladine, C. R.: Modal stiffnesses of a pretensioned cable net. Int. J. Solids Structures, Vol. 18, No. 10, 1982, pp. 829-846.
- https://www.archinform.net/projekte/126.htm
- https://archello.com/project/the-new-beijing-poly-plaza-2
- https://www.broadwayglass.us/case-view/217.html
- https://seele.com/references/sowwah-square
- Sobek, W., Feirabend, S., Blandini, L. a Tarazi, F.: Cable-stayed glass facades – 15 years of innovation at the cutting edge. Conf. Challenging Glass 2, Veer (TU Delft), 2010, 9 s.
- Talvik, I.: Finite element modelling of cable-networks with flexible supports. Computers and Structures, Vol. 79, No. 26-28, 2001, s. 2443-2450.
- Wang, Y. Q., Wu, L. L., Shi, Y. J., Sun, F., Luo, K., Xu, Y.: FEM analysis and experimental study on monolayer cable-net for glass facades: Static performance. Advances in Structural Engineering, Vol. 10, No. 4, 2006, s. 371-382.
- Ming, L., Liguo, W., Yuanqing, W., Wei, T., Bin, W., Renliang, S.: Analysis on prestress application for cable net supported curtain wall. Int. Conf. On Mechatronics, Electronic, Industrial and Control Engineering, Atlantis Press, 2015, s. 607-610.
- Shi, Y. J, Wu, L., Wang, Y. Q., Luo, K., Xu, Y.: FEM analysis and experimental study on monolayer cable-net for glass facades: Dynamic properties, Advances in Structural Engineering, Vol. 10. 4., 2007, s. 383-395.
- Feng, R. Q., Zhang, L. L., Wu, Y., Shen S. Z.: Dynamic performance of cable-net facade. J. Constructional Steel Research. No. 65, 2009, s. 2217-2227.
- Feng, R. Q., Ye, J. H., Wu, Y., Shen, S. Z.: Nonlinear response spectra of cable net facades. Soil Dynamics and Earthquake Engineering, Vol. 32, No. 1, 2012, s. 71-80.
- Zaimovic, A., Medic, S., Dolarevic, S.: Static and dynamic analysis of nonlinear elastic cables. 8th Int. Congress of Croatian Society of Mechanics, 2015, 13 s.
- Yang, L., Shi, G., Yin, H., Shi, X., Guo, Z.: Full-scale experimental study on the influence of damages on the static behavior of the single-layer cable net structure. Structures, Vol. 3, 2015, s. 153-162.
- Shang, C. D.: Numerical simulation and analysis of the mechanical behaviour of cable supported glass façades. PhD Thesis, UPC University of Barcelona, 2014, 171 s.
- Yussof, M. M., Parke, G., Kamarudin, M. K.: Glass stiffness contribution on flat and curved cable-net supported glass facade systems. 3rd Int. Conf. On Civil Engineering Research, Surabaya, 2017, s. 531-536.
- Piyasena, R. R. C., Thambiratnam, D. P., Chan, T. H. T., Perera, N. J.: Comparative analysis of blast response of cable truss and cable net façades, Eng. Failure Analysis, Vol. 104, 2019, s. 740-757.
- Royer-Carfagni, G., Viviani, L.: Basic design of cable-supported glazed surfaces under blast waves. Int. J. of Non-linear Mechanics, Volume 123, 2020, 103489.
- Marzuki, N. A., Yussof, M. M., Keong, C. K., Min, Y. H.: Experimental performance of the cable-net structure supported glass systems with cable damages. AIP Conf. Proc. 2239, 2020, s. 0200301-0200309.
- Khalkhaliha, M., Zarfam, P., Zarfam, R.: Vibration Control of Cable Net Façade by Smart Supports. Structural Engineering Int., Vol. 32, No. 4, 2022, s. 1-7.
- Komlev, V., Macháček, J.: Lanové sítě pro skleněné fasády – Návrh a parametrické studie. TZB-info, ocelové konstrukce, 2023.
- https://www.strand7.com/
Poděkování
Článek a související výzkum vznikl za podpory grantu ČVUT SGS22/141/OHK1/3T/11.
Článek se zabývá přehledem vývoje a vybranými aktuálními poznatky lanových konstrukcí využívaných jako součást nosného systému skleněných fasád. Článek je přehledový a rozsahem a hloubkou záběru je přiměřený. Článek doporučuji k publikování .
The article deals with preliminary information on design of prestressed cable-nets supporting large glass façades. Described are façade components and examples of prominent realized façades. In the survey of primary publications the trend of experimental and theoretical approaches concerning design problems of these structures is presented (securing of necessary stiffness and load capacity, danger of a glass-cable-net connection failure, failure of anchors or loss of prestressing, dynamic behaviour during failures, blasts and earthquakes, temperature effects). In more details are described publications used in the follow-up Part [31] for validation and verification of the own numerical analysis and parametric studies of these façades.








![Obr. 4a Vrstvené sklo (např. 6+2×0,38+6 = 12,76 [mm])](/docu/clanky/0260/026015o18.png)
![Obr. 4b Tepelně izolační trojsklo (např. 4+14Ar+4+14Ar+4 = 40 [mm])](/docu/clanky/0260/026015o20.png)