Aktuální problematika navrhování tesařských spojů
Růst nároků na environmentální prostředí, udržitelnost výstavby a zdravých životních podmínek vyvolal především v Evropě vyšší poptávku po konstrukcích ze dřeva. Rychlost a přesnost CNC opracování dřevěných konstrukčních prvků umožňuje efektivní výrobu dřevostaveb tradičními tesařskými postupy. Příspěvek reaguje na aktuální problematiku návrhových postupů pro výpočet únosnosti tradičních tesařských spojů. Tento způsob propojení prvků nemá velkou oporu v současně platných normách, a proto návrh spočívá v použití jednoduchých empirických vztahů, které vycházejí ze zkušenosti. Tento článek prezentuje experimentální a výpočetní metody pro vyšetřování statického chování a únosnosti tesařských spojů.
1. Úvod
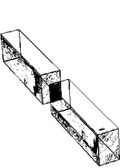
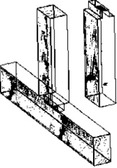
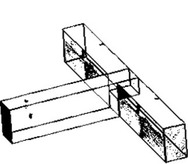
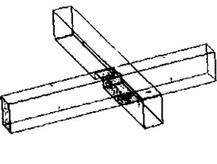
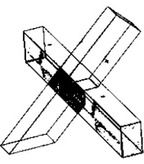
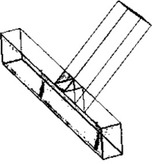
Spoje dřevěných konstrukcí je možné rozdělit na mechanicky spojované a lepené. Lepené konstrukční spoje nacházejí své uplatnění především v halové výstavbě např. zemědělského nebo sportovního charakteru. Mechanicky spojované spoje je možné dále dělit na spoje s kovovými spojovacími prostředky (hřebíkové, svorníkové, vrutové, kolíkové, sponkové, hmoždíkové, s perforovanými deskami s prolisovanými trny, s ocelovými úhelníky, apod.) a na spoje tesařské. Tesařské spojování získává v poslední době oblibu právě díky efektivní výrobě pomocí CNC strojů, estetice výsledného spoje a také vyšší požární odolnosti ve srovnání s kovovými spojovacími prostředky. Na obrázku 1 jsou patrné kategorie podélných a příčných tesařských spojů podle základního dělení.
sraz
plátování
lípnutí
zapuštění
čepování
přeplátování
kampování
osedlání
zadrápnutí
Obr. 1. Základní rozdělení tesařských spojů
2. Navrhování tesařských spojů
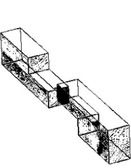
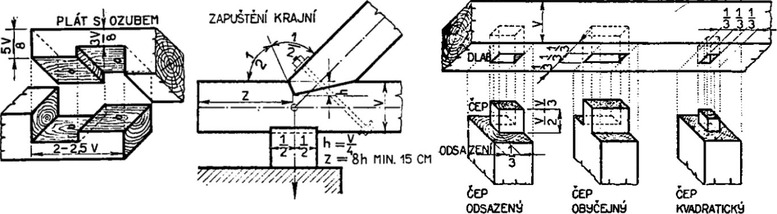
Z historického pohledu vycházel návrh tesařských spojů z jednoduchých empirických vztahů, které byly založeny na předávání řemeslných zkušeností tesařských mistrů. Tyto tesařské poučky obvykle spočívaly v určení velikosti oslabení trámů vzhledem k jejich rozměrům. Dodnes se tesaři těmito znalostmi řídí a s ohledem na další okrajové podmínky (např. kvalita řeziva, poloha spoje v konstrukci, apod.) mírně modifikují zažité geometrické parametry. Na obrázku 2 jsou znázorněny vybrané tesařské spoje s doporučenými rozměry opracovávaných částí spojů podle Sedláka [1].
Obr. 2. Empirické vztahy vycházející ze zkušenosti
Tyto empirické vztahy nedostačují současným požadavkům a je potřeba tesařské spoje posoudit na statické namáhání. V platných technických normách není bohužel dostatečná opora návrhových postupů pro tesařské spojování. Statici a projektanti jsou nuceni vycházet z jednoduchého rozkladu sil ve spojích a ze základních posudků tlakového a smykového napětí.
Evropská norma ČSN EN 1995-1-1 [2] uvádí základní podmínky pro posouzení tlakového a smykového napětí:
tlak rovnoběžně s vlákny dřeva:
(1)
tlak kolmo k vláknům dřeva:
(2)
tlak šikmo k vláknům dřeva:
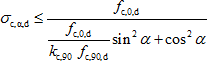(3)
smyk:
(4)
kde σc,0,d je návrhové napětí v tlaku rovnoběžně s vlákny dřeva, NEd je návrhové tlakové zatížení, Aef je účinná kontaktní plocha, fc,0,d je návrhová pevnost dřeva v tlaku rovnoběžně k jeho vláknům, σc,90,d je návrhové napětí v tlaku kolmo k vláknům dřeva, kc,90 je součinitel zohledňující uspořádání zatížení, možnost štěpení a stupeň deformace v tlaku, fc,90,d je návrhová pevnost dřeva v tlaku kolmo k jeho vláknům, σc,α,d je návrhové napětí v tlaku šikmo k vláknům dřeva, α je úhel mezi směrem působící síly a směrem vláken dřeva, τv,d je návrhové napětí ve smyku, VEd je návrhové smykové zatížení, kc,r je součinitel vlivu výsušných trhlin, b je šířka smykové plochy, h je výška (délka) smykové plochy, fv,d je návrhová pevnost dřeva ve smyku.
Obr. 3. Označení geometrických parametrů a síly pro výpočet
Další současně platná norma ČSN 73 1702 [3], která je modifikovaným překladem německé normy DIN 1052 [4] uvádí výpočetní postupy pro zapuštění a čepové spoje. Výpočet zapuštění podle této normy obsahuje stanovení maximální hloubky zářezu a posouzení napětí v tlaku šikmo k vláknům a ve smyku:
U zapuštění má hloubka zářezu tv splňovat podmínky:
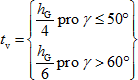(5)
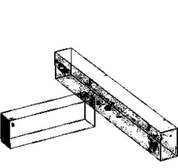
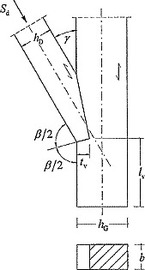
Geometrické parametry jsou patrné z obrázku 3. Mezní hodnoty lze interpolovat podle přímky. Při dvoustranném zapuštění smí být hloubka každého zářezu nezávisle na úhlu připojení nejvýše 1/6 výšky hG dřevěného prvku se zářezem.
Návrhová hodnota únosnosti zapuštění vychází z návrhové hodnoty pevnosti v tlaku v čelní ploše zapuštění. Napětí v tlaku v čelní ploše zapuštění lze posuzovat takto:
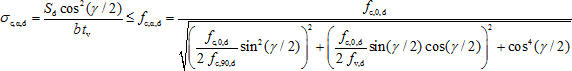(6)
Tlaková složka síly rovnoběžná s dřevěným prvkem se zářezem vyvozuje v dřevěném prvku se zářezem napětí ve smyku, které lze uvažovat rovnoměrné rozdělené. Délky zhlaví větší než 8 tv se v tomto případě nesmí uvažovat ve výpočtu. Je třeba zajistit polohu jednotlivých částí spojovaných zapuštěním, např. pomocí svorníků.
Napětí ve smyku ve zhlaví lze posoudit takto:
(7)
Analytické vztahy pro výpočet napětí nejčastěji používaných spojů v českých zemích uvádí Vinař a Kufner [5]. Výpočty vycházejí z rozkladu sil a stanovení napětí v kritických částech spojů.
3. Vědecko-výzkumné metody tesařských spojů
Jednoduché analytické vztahy dávají představu o únosnosti tesařských spojů, ale chování spoje v průběhu zatížení nezachycují. Následující metody slouží k popisu chování spojů a určení jejich únosností, případně míst porušení spojů.
Nejprůkaznější metoda ke stanovení chování a únosnosti tesařských spojů je experimentální destruktivní zkouška. Spoje se nejčastěji zkouší ve skutečném měřítku. Zkouška se obvykle provádí na statisticky přijatelném počtu vzorků. Vysoký počet vzorků je potřebný zejména při zkoušení materiálu vzhledem k různorodosti a vadám dřeva. Bohužel je tato metoda finančně náročná.
Další metodou ke stanovení chování spojů je digitální korelace obrazu. Metoda spočívá v pořizování fotografií (ve vysokém rozlišení) spoje během experimentu v určitých časových intervalech. Povrch zkušebního vzorku je obvykle opatřen sítí bodů k snazšímu zachycení jejich posunů. Při porovnání jednotlivých snímků je možné velice přesně určit posuny bodů v síti, deformace spoje a stanovit tok napětí ve spojovaných elementech.
S rozvojem výpočetní techniky a matematických postupů (např. MKP – metoda konečných prvků) přichází možnost numericky řešit idealizované modely skutečných konstrukčních řešení. Tyto modely tvoří základ pro stanovení průběhu a velikosti napětí i deformací v modelovaných částech konstrukce. Při dobré shodě výsledků numerické simulace s experimenty je možné omezit počet laboratorních zkoušek a tím urychlit a zlevnit výzkum.
Metoda komponent podložená vědecko-výzkumnou činností je vhodná pro praktické navrhování. Tato metoda se uplatňuje ve výpočtech ocelových styčníků, ale je použitelná i pro spoje dřevěných konstrukcí. Metoda komponent rozděluje tesařský detail na soustavu tzv. komponent, které popisují jednotlivé části spoje pomocí tuhosti pružin. Metodu komponent v souvislosti s tesařskými spoji použil ve svém výzkumu Wald s kolektivem [6].
4. Závěr
Příspěvek shrnuje aktuální problematiku navrhování tradičních tesařských spojů v souvislosti s historickými pravidly, normativními postupy a vědecko-výzkumnými metodami. V článku je uvedeno základní dělení tesařských spojů, příklady empirických vztahů a návrhové postupy popsané v současně platných normách. Prezentovány jsou také metody vědecko-výzkumné činnosti k reálnému popisu chování, únosnosti a módů porušení tesařských spojení.
Poděkování
Tento příspěvek vznikl za finanční podpory MŠMT v rámci programu NPU I č. LO1605 – Univerzitní centrum energeticky efektivních budov – Fáze udržitelnosti.
Literatura
- SEDLÁK, J. Tesařství. Praha: B. Pyšvejc, 1948.
- ČSN EN 1995-1-1. Eurokód 5: Navrhování dřevěných konstrukcí - část 1-1: Obecná pravidla pro pozemní stavby. Praha: Český normalizační institut, 2006.
- ČSN 73 1702. Navrhování, výpočet a posuzování dřevěných stavebních konstrukcí – Obecná pravidla pro pozemní …. Praha: Český normalizační institut, 2007.
- DIN 1052:2004. Entwurf, Berechnung und Bemessung von Holzbauwerk. Allgemeine bemessungsregeln und bemessungsregeln fur den hochbau, 2004.
- VINAŘ, J. a V. KUFNER. Historické krovy: konstrukce a statika. Praha: Grada, 2004.
- WALD, F. et al. Component method for historical timber joints. The Paramount Role of Joints into the Reliable Response of Structures, 4, 2000.
A growing environmental awareness and desire for sustainable solutions and healthy living conditions, especially in Europe, lead to an increasing demand for timber structures. High speed, excellent cut quality and accuracy of CNC processing allows an effective produce of timber structures by traditional carpentry procedures. This article responds to current problem of load bearing capacity calculations of traditional carpentry joints. This way of structural joints has not sufficient support in current standards and therefore design relies on simple empirical relationships based on experience. This paper presents the experimental and calculation methods for investigation of static behaviour and load bearing capacity of carpentry joints.