Polotuhé pôsobenie prípojov v drevených konštrukciách
Moderné spojovacie prostriedky ponúkajú nové možnosti v navrhovaní drevených nosných konštrukcií. Skryté prefabrikované kovové prvky sú zaujímavým riešením pre architektov a investorov. Niektoré spojovacie prvky svojou geometriou môžu prispieť k polotuhému pôsobeniu prípojov. U inžinierov-statikov vzniká často otázka, či je postačujúce uvažovať s kĺbovým pôsobením prípojov? S rastúcimi skúsenosťami v oblasti navrhovania drevených konštrukcií rastie aj tendencia rozšírenia tradičného kĺbového pôsobenia k polotuhým pôsobením spojov. Článok prezentuje výpočet konkrétneho polotuhého spoja, kde bol použitý prefabrikovaný kovový prvok AluMidi od firmy Rothoblaas kombinovaný s hladkými aj samoreznými kolíkmi a rebierkovými klincami. Článok predstavuje koncept výpočtu prípoja vedľajšieho nosníka na hlavný nosník s polotuhým pôsobením. Uvádzaná problematika je súčasťou diplomovej práce na Stavebnej fakulte STU v Bratislave.
Úvod
Prípoje drevených konštrukcií sa v bežnej praxi uvažujú s kĺbovým charakterom, teda umožňujúce voľné pootočenie. Výrobcovia spojovacích prostriedkov ponúkajú v dnešnej dobe veľmi širokú škálu kovových prvkov, z ktorých mnohé umožňujú polotuhé pôsobenie. Jedným príkladom je kovový prvok AluMidi, ktorý môže zabezpečiť istý stupeň votknutia. Koncept s kĺbovým pôsobením prípojov je vo väčšine prípadov bezpečné niekedy až konzervatívne.
Polotuhé pôsobenie spojov je stále častejšie využívané pri navrhovaní nosných konštrukcií. Zvýšenie presnosti výpočtu sa potom môže prejaviť aj v ekonomických ukazovateľoch. Na výpočet tuhostí spoja bol použitý prefabrikovaný spojovací prostriedok firmy Rothoblaas, skrytý T-kus AluMidi v kombinácií s kolíkmi a klincami.
Prvým krokom návrhu je výpočet vychádzajúci z bežného kĺbového pôsobenia prípoja. Podrobnejší postup zahŕňa výpočet tuhosti prípoja a spätná analýza vnútorných síl pri uvážení konkrétnej tuhosti.
Tuhosť prostriedku je závislá od počtu a rozmiestnenia spojovacích prostriedkov. V nasledujúcej časti je ukázaný spomínaný postup a rozdiely v pôsobení spojov.
Vstupné údaje
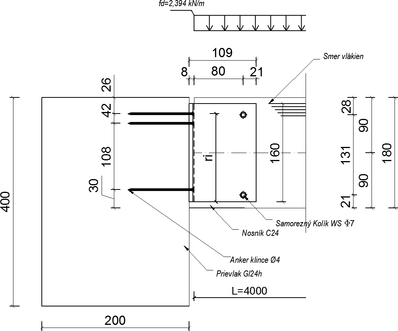
Na hlavný nosník z lepeného lamelového dreva pevnostnej triedy GL24h a rozmermi 200/400 mm je pripojený vedľajší nosník z rasteného dreva triedy C24 a rozmermi 100/180 mm pomocou kovového prvku AluMidi, klincov a kolíkov. Vedľajší nosník je zaťažený rovnomerným spojitým zaťažením (Obr. 1. a 2.) Geometrické údaje sú zhrnuté v tabuľke 1.
Schéma č. 1 – Statická schéma s kĺbovým pôsobením
Schéma č. 2 – Statická schéma polotuhého prípoja obsahujúce dve tuhosti, a to tuhosť kolíkového (ko pre časť „a“) a tuhosť klincového spoja (kl pre časť „b“)
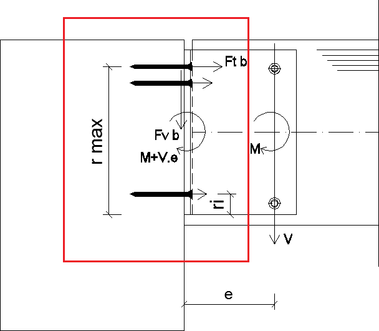
Obr. 1: Statická schéma kĺbového a polotuhého modelu
| Statický model | Ohybový moment [kNm] | |
|---|---|---|
| Nadpodperový | Medzipodperový | |
| Kĺbový | 0 | 4,79 |
| Polotuhý | 0,51 | 4,28 |
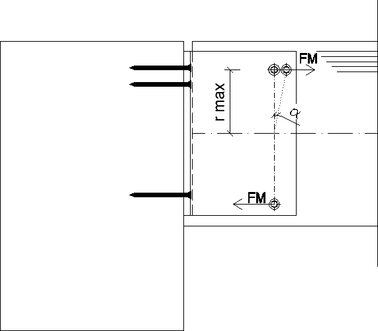
Prípoj vedľajšieho nosníka na kovový prvok (časť „a“) bol navrhnutý so samoreznými kolíkmi typu WS s priemerom 7 mm (Obr. 2). Samorezný kolík WS je vyrobený u uhlíkovej ocele s bielym galvanickým zinkovaním. Konektory umožňujú vytvárať tuhé spoje schopné prenášať namáhanie ohybovým momentom. Zmenšený priemer tiež zaisťuje vynikajúcu ťažnosť a duktilitu a je ideálne aj pre seizmické projektovanie.
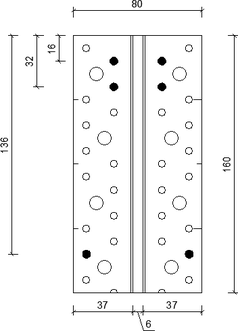
Prípoj kovového prvku AluMidi na hlavný nosník (časť „b“) je zabezpečený prostredníctvom klincov typu LBA, ktoré majú rebrované telo pre lepšiu odolnosť voči vytiahnutiu z dreva. Ďalšou možnou alternatívou je použitie skrutky.
Obr. 2 – Samorezný kolík WS (Zdroj: Rothoblaas)
Obr. 3 – AluMidi (Zdroj: Rothoblaas)
| Spojovacia časť | Rozmery [mm] | ||
|---|---|---|---|
| Hlavný nosník | Výška prierezu | hpr | 400 |
| Šírka prierezu | bpr | 200 | |
| Vedľajší nosník | Výška prierezu | hse | 180 |
| Šírka prierezu | bse | 100 | |
| Dĺžka | L | 4 000 | |
| AluMidi 160 (bez otvorov) | Výška | H | 160 |
| Dĺžka vystupujúcej časti | LB | 109,4 | |
| Hrúbka | t | 6 | |
| Samorezný kolík WS | Nominálny priemer | d1 | 7 |
| Dĺžka | L | 93 | |
| Klince | Nominálny priemer | d1 | 4 |
| Dĺžka | L | 100 | |
Obr. 4 – Detail spoja (priečny rez hlavným nosníkom)
Obr. 5 – Detail rozmiestnenia klincov na konzolke AluMidi
Vypočítané namáhanie prípoja
Obr. 6 – Namáhanie kolíkov pri kĺbovom pôsobení (časť „a“)
Obr. 7 – Namáhanie kolíkov pri polotuhom pôsobení (časť „a“)
Namáhanie jedného spojovacieho prostriedku časti „a“ (kolíka) spôsobené ohybovým momentom
(1)
kde je
- FM
- horizontálna sila od momentu Mi v kN,
- M
- ohybový moment v kNm,
- ri
- vzdialenosť medzi dvoma spojovacími prostriedkami v mm.
Namáhanie jedného spojovacieho prostriedku časti „a“ (kolíka) od účinku priečnej sily:
(2)
kde je
- V
- návrhová priečna sila v prípoji v kN,
- n
- počet spojovacích prvkov,
- FV
- priečna sila na 1 spojovací prostriedok.
Obr. 8 – Namáhanie klincov (časť „b“)
Výpočet horizontálnej ťahovej sily Ft od pôsobenia ohybového momentu na jeden spojovací prostriedok časti „b“ (klinec):
(3)
kde je
- Ft.b
- horizontálna sila od momentu v kN,
- M
- ohybový moment jednotkový v kNm,
- ri
- vzdialenosť od hrany plechu k ťažisku spojovacieho prostriedku v mm,
- V
- návrhová priečna sila v prípoji v kN,
- e
- excentricita návrhovej sily V v m.
Výpočet sily na jeden spojovací prostriedok (klinec) časti „b“ od účinku priečnej sily:
(4)
kde je
- FV.b
- návrhová priečna sila v prípoji v kN,
- n
- počet spojovacích prvkov,
- FV.b1
- priečna sila na 1 spojovací prostriedok.
Pozn.: kĺbový model je zaťažený jednotkovým ohybovým momentom, pomocou ktorého vypočítame tuhosť spoja.
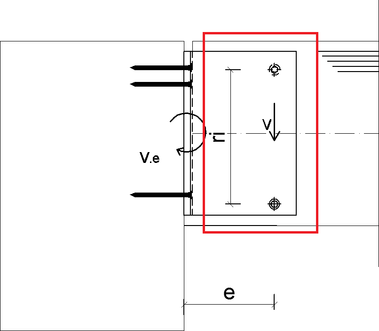
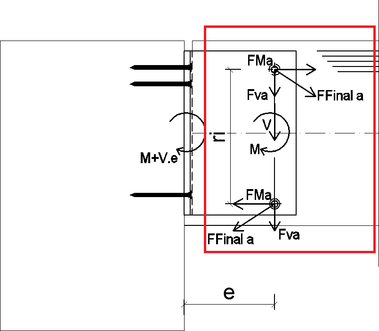
V prípade kĺbového pôsobenia je spoj namáhaný len priečnou silou a malým ohybovým momentom od excentrického pripojenia kolíkov. Ohybový moment ktorý vzniká v dôsledku polotuhého pôsobenia spoja sa prenáša pomocou koncovky AluMidi, ktorá sa oprie o hlavný nosník. Následkom polotuhého pôsobenia sa zvýšia sily v spojovacích prostriedkov. Kolíky v časti „a“ budú namáhané aj zložkou z ohybového momentu (Obr. 7). Výslednica z priečnej sily a zo sily spôsobenej momentom bude pôsobiť v menšom uhle voči smeru vláken v porovnaní s kĺbovým modelom. To znamená priaznivejšie využitie spoja, lebo odolnosť v smere vláken je väčšia ako kolmo na vlákna.
Výpočet tuhosti spoja
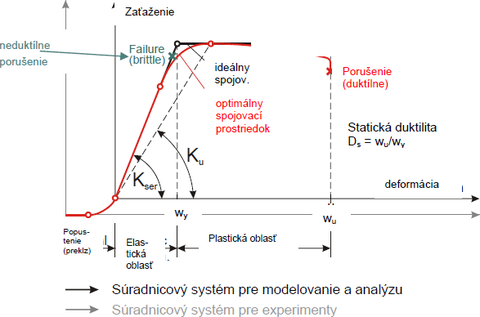
Pre výpočet tuhosti spoja potrebujeme poznať pracovný diagram spojovacieho prostriedku (Obr. 9). Z diagramu je možné určiť moduly popustenia Kser (N/mm) pre medzný stav používateľnosti a Ku = 2/3 Kser pre medzný stav únosnosti. Moduly popustenia pre rôzne spojovacie prostriedky pri namáhaní strihom sú uvedené v tab. 3.
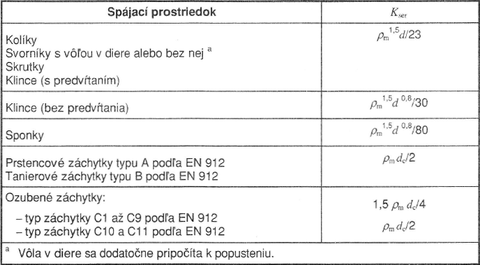
Tab. 3 – Hodnoty Kser spájacieho prostriedku podľa STN EN 1995-1-1
Tuhosť spojov ovplyvňuje vo všeobecnosti celkovú deformáciu drevenej konštrukcie.
Obr. 9 – Pracovný diagram (Schickhofer, 2006)
Pre kolíky bez predvŕtania sa moduly popustenia určia nasledovne:
(5)
kde je
- ρm
- priemerná hustota dreva a ocele T-kusu AluMidi cez ktorý prechádza kolík v kg/m3,
- d
- priemer spojovacieho prostriedku.
Posun spojovacieho prvku od konkrétnej sily FM sa určí podľa vzťahu (6) pre medzný stav používateľnosti a podľa (7) pre medzný stav únosnosti.
(6)
kde je
- uinst Kser
- posun spojovacieho prvku pre MSP v mm,
- FM
- horizontálna sila od momentu Mi v kN,
- Kser
- modul popustenia v N/mm.
(7)
kde je
- uinst Ku
- posun spojovacieho prvku pre MSU v mm,
- FM
- sila od momentu Mi v kN,
- Ku
- modul popustenia 2/3 Kser v N/mm.
Obr. 10 – Posun spojovacieho prostriedku uinst pri polotuhom pôsobení
Z vypočítaného posunu sa určí uhol pootočenie prípoja. Výslednú tuhosť vypočítame pre jednotkové pootočenie v MNm/rad.
Podobným postupom sa určí aj tuhosť klincového spoja časti „b“. Rozdiel je v spôsobe namáhania klincov. Tuhosť klincového spoja, namáhaného pozdĺž osi ťahovou silou, je možné určiť podľa dokumentu ETA-13/0029, kde sa tuhosť určuje ako 100násobok efektívnej dĺžky. Výsledné tuhosti kolíkového a klincového spoja budú odlišné.
Obr. 11 – Statická schéma polotuhého prípoja obsahujúce dve tuhosti, a to tuhosť kolíkového (ko pre časť „a“) a tuhosť klincového spoja (kl pre časť „b“)
Pri pôsobení polotuhého spojenia vznikajú malé hodnoty momentov v podperách. Hodnoty medzipodperových momentov sú o 12 % menšie.
Výsledná sila v kolíku bude väčšia, ale uhol výslednice voči smeru vláken je priaznivejší ako pri kĺbovom pôsobení. Preto je využitie kolíka o 26 % nižšia.
Namáhanie klincov kvôli momentu je síce väčšie o asi 25 %. Využitie klincov je možné upraviť vhodnejším rozmiestnením po výške. Aj keď vzrastie počet klincov v prípoji, treba poznamenať, že ich podiel na cene celého diela je minimálny.
Záver
Reálne pôsobenie prípojov v drevených konštrukciách je možné modelovať zohľadnením konkrétnych tuhostí spojovacích prostriedkov. Podrobné výpočty lepšie popisujú charakter prípojov a výsledky sa môžu prejaviť nielen v bezpečnosti, ale aj v ekonomickej oblasti. Vplyvom tuhostí konkrétnych prípojov dochádza k inému rozdeleniu vnútorných síl ako v prípade bežných kĺbových modeloch. Uvádzané teoretické modely budú experimentálne overené a predstavené v rámci diplomovej práce Attilu Rácza. Experimentálnym overovaním sa budú overovať tuhosti konkrétnych prípojov pre potvrdenie predstavených názorov. V drevených konštrukciách existuje iba málo typov prípojov, ktoré sú dokonale kĺbové. Podobne je možné konštatovať, že úvaha o dokonale tuhých rámových spojoch je takmer vylúčená. Veľká väčšina prípojov si vyžaduje špeciálny prístup z hľadiska reálnej tuhosti.
Literatúra
- European Technical Approval ETA-13/0029. Würth self-tapping screw. Self-tapping screws for use in wood-concrete slab kits.
- Sandanus, J. – Sógel, K. (2010): Drevené nosné konštrukcie – príklady. Nakladateľstvo STU, 2010
- Schickhofer, G. (2006): Holzbau, Nachweisführungen für Konstruktionen aus Holz. Institut für Holzbau und Holztechnologie, TU Graz, S-4-01B/2006
- STN EN 1995-1-1 – Navrhovanie drevených konštrukcií, SÚTN, 2008
- STN EN 380 – Skúšobné metódy, SÚTN, 1998
- Wood Connectors and Timber Plates, www.rothoblaas.com, (online, prístupné dňa 3. 5. 2017), dostupné na:
https://issuu.com/rothoblaas/docs/plates-and-connectors-for-wood-en__?e=18207635/13893089
Modern fasteners offer new possibilities in the design of timber load-bearing structures. Concealed prefabricated metal elements are an interesting solution for architects and contractors. Through their geometry, some fasteners are able to ensure semi-rigid behaviour in the connection. The question is whether the assumption of hinge behaviour of a connection in the design of timber structures is sufficient. The tendency of semi-rigid consideration is growing with the experiences in the field of design of timber structures. The paper presents the calculation of a semi-rigid connection, where the concealed metal element AluMidi made by Rothoblaas is used and combined with self-perforating dowels and threaded nails. The paper presents the connection of the secondary beam to the primary beam and the idea of semi-rigid operation. The demonstrated topic is a part of master’s thesis at Slovak University of Technology in Bratislava.