Zdivo sevřené a seizmicky zatížené konstrukce
Přehrát audio verzi
Zdivo sevřené a seizmicky zatížené konstrukce
00:00
00:00
1x
- 0.25x
- 0.5x
- 0.75x
- 1x
- 1.25x
- 1.5x
- 2x
Sevřeným zdivem (confined masonry) ve smyslu ČSN EN 1996-1-1:2023], dále EC6_2G, se rozumí zdivo, které je dodatečně (po vyzdění) obetonované železobetonovými ztužujícími prvky nebo prvky z vyztuženého zdiva. Tyto ztužující prvky zdivo svírají tak, aby všechny materiály spolupůsobily proti účinku zatížení. V žádném případě se nejedná o železobetonový skelet dodatečně vyzdívaný, kde je opačný postup výstavby (nejprve betonáž ŽB prvků a následně zdění). Text připomíná konstrukční zásady pro sevřené zdivo, včetně několika příkladů.
1. Úvod
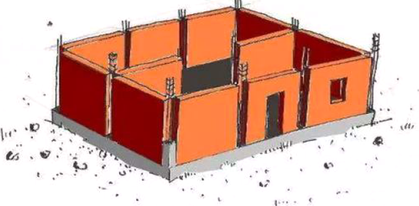
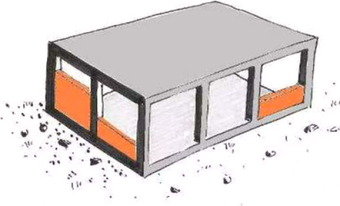
Sevřeným zdivem (confined masonry) ve smyslu ČSN EN 1996-1-1:2023 [1], dále EC6_2G, se rozumí zdivo, které je dodatečně (po vyzdění) obetonované železobetonovými ztužujícími prvky nebo prvky z vyztuženého zdiva. Tyto ztužující prvky zdivo svírají tak, aby všechny materiály spolupůsobily proti účinku zatížení. V žádném případě se nejedná o železobetonový skelet dodatečně vyzdívaný, kde je opačný postup výstavby (nejprve betonáž ŽB prvků a následně zdění). Rozdíl technologie sevřeného zdiva a vyzdívaného skeletu je zobrazen na obr. 1.
Obr. 1 Postup výstavby: a) sevřeného zdiva s vodorovnými a svislými ztužujícími prvky; b) vyzdívaného ŽB skeletu
Nový EC6_2G zavádí některá aplikační pravidla. Předchozí vydání ČSN EN 1996-1-1+A1 [2], dále EC6_1G, obsahovalo jen zásady pro navrhování. Rovněž byly velmi rozšířeny konstrukční zásady pro sevřené zdivo, anebo některé stávající konstrukční zásady byly drobně upraveny.
Informace o sevřeném zdivu ve světě, jako jsou používané konstrukční zásady pro provádění i metody návrhu těchto konstrukcí, lze najít např. na portále projektu Confined Masonry Network [3]. Ve vazbě na EC6_2G jsou důležité publikace týmu Marques at al. [4, 5, 6], kde jsou popsány a komentovány návrhy na úpravu EC6 i jejich porovnání jednak s ostatními metodami používanými ve světě a jednak s experimentálními zkouškami.
Uvádí se [5], že první provedení staveb ze sevřeného zdiva bylo v Itálii po katastrofálním zemětřeseních v italské Messině v roce 1908, a potom v Chile po zemětřesní „Talca earthquake“ v roce 1928. Konstrukcemi ze sevřeného zdiva byla snaha naplnit oprávněný požadavek, aby nově budované tradiční zděné stavby byly odolnější k účinkům zemětřesení. Sevřené zdivo se poté osvědčilo při dalším zemětřesení v Chile v roce 1939, a proto se toto konstrukční řešení šířilo dále do většiny států Latinské Ameriky a později do států na všech kontinentech (Indie, Nový Zéland, Japonsko, Kanada, Slovinsko atd.).
Mezi evropské země, kde se využívá delší dobu sevřené zdivo, se řadí Itálie, Srbsko, Slovinsko, celý Balkánský poloostrov, Rumunsko a určité zkušenosti jsou také z Řecka a Portugalska. Je uváděn potenciál k použití těchto konstrukcí ve Španělsku, Švýcarsku, na Islandu a Kypru [4].
Z výše uvedeného je zřejmé, že navrhování sevřeného zdiva je spojeno s návrhem konstrukce na seizmickou návrhovou situaci dle EC8. Nová generace EC8 v době přípravy této publikace nebyla v úplnosti vydána. V současnosti platná ČSN EN 1998-1:2013 [7], dále EC8_1G, bude v druhé generaci rozšířena a rozdělena do 2 částí, a to 1. část „actions“ a 2. část „building“. EN 1998-1-1 byla schválena v roce 2024 a EN 1998-1-2 čeká na finální schválení v říjnu 2025, tyto předpisy budou dále označovány EC8_2G.
2. Konstrukční zásady pro sevřené zdivo
V konstrukčních zásadách EC6_2G je uveden základní požadavek na vybetonování ztužujících prvků až po dokončení zděné stěny, což je hlavní znak sevřeného zdiva. Je tak docíleno většího spolupůsobení zdiva a ztužujících ŽB prvků jako jednoho celku při seizmicitě.
Předpis EC6_2G nepokrývá sevřené zdivo ze zdicích prvků skupiny 4 (s vodorovnými otvory). Jinak další požadavky na zdicí prvky neuvádí.
Zdicí malty používané v sevřeném zdivu nemají mít průměrnou pevnost v tlaku fm menší než 5 MPa; v případě použití prefabrikované výztuže ložných spár nemá být fm menší než 2 MPa.
Charakteristická pevnost betonu v tlaku pro ztužující prvky sevřeného zdiva nemá být menší než větší z hodnot pevnosti v tlaku zdiva nebo než 20 MPa. V případech, kdy jsou výztužné prvky sevřeného zdiva tvořeny ze speciálních zdicích prvků, nemá být pevnost malty v tlaku menší než větší z hodnot pevnosti v tlaku zdiva nebo než 10 MPa.
Ztužující prvky pro sevření zdiva se umístí v úrovni každého stropu, v každém křížení stěn a podél obou okrajů otvorů o ploše větší 1,5 m2. Doplňkové ztužující prvky pro sevření zdiva by se měly navrhnout tehdy, když jejich vzdálenost by byla ve svislém směru větší než 5 m a ve vodorovném směru větší než 4 m.
Ztužující prvky pro sevření zdiva mají mít průřezovou plochu nejméně 0,02 m2 při nejmenším rozměru v rovině stěny 150 mm a mají být opatřeny podélnou výztuží o průřezové ploše nejméně 0,8 % průřezu výztužného prvku pro sevření a alespoň 200 mm2 nebo 4 pruty výztuže průměru 8 mm.
Mají se také provést třmínky o průměru ≥ 5 mm o vzdálenosti rovné menší z hodnot 250 mm nebo tloušťka stěny. Do vzdálenosti 0,6 m od konců ztužujících prvků nemá být osová vzdálenost třmínků větší než 150 mm. (Dříve v EC6_1G byly třmínky průměru nejméně 6 mm ve vzdálenosti nejméně 300 mm.)
Podle EC6_2G mají být splněny určité požadavky pro zajištění spolupůsobení ztužujících prvků a zdiva. U sevřeného zdiva se mají zdicí prvky, které navazují na ztužující prvky pro sevření, vzájemně přesahovat podle ustanovení pro vazbu zdiva. Alternativně se má provést vyztužení pruty o průměru alespoň 5 mm, které jsou umístěny ve vzdálenosti nanejvýš 300 mm a plně zakotveny do výplňového betonu a maltových spár. Aby se zlepšilo spolupůsobení mezi zděnou stěnou a ztužujícími prvky, mohou být prvky provedeny jako zazubené.
Je třeba upozornit, že EC8_1G obsahuje další konstrukční zásady a požadavky pro sevřené zdivo při seizmické návrhové situaci, které jsou mnohdy přísnější než ustanovení v EC6_2G. Je proto třeba ověřit i ustanovení v EC8_2G, který v době přípravy tohoto textu nebyl vydán.
3. Posuzování mezích stavů únosnosti sevřeného zdiva
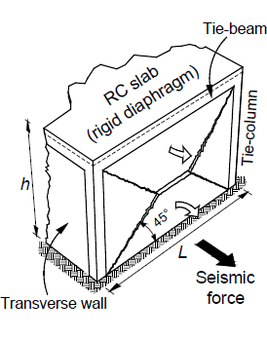
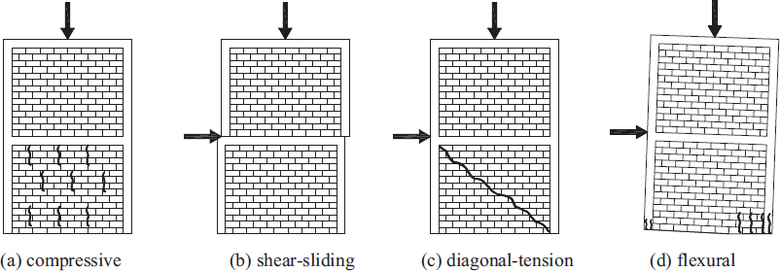
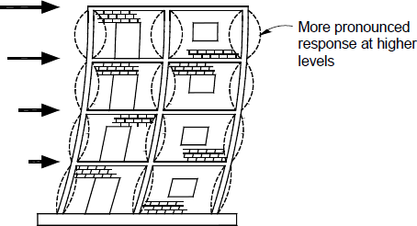
Pro posuzování mezních stavů únosnosti sevřeného zdiva se vychází ze způsobů porušení, které může být jednak v tlaku, ohybem a/nebo smykem v rovině zdiva, viz obr. 2 a 3a. Také to může být zatížení kolmo na rovinu zdiva vlivem setrvačných sil při seizmicitě, viz obr. 3b.
Obr. 3 Rozhodující způsoby porušení pro seizmickou návrhovou situaci: a) zatížení smykem a/nebo ohybem v rovině; b) příčné zatížení zdiva
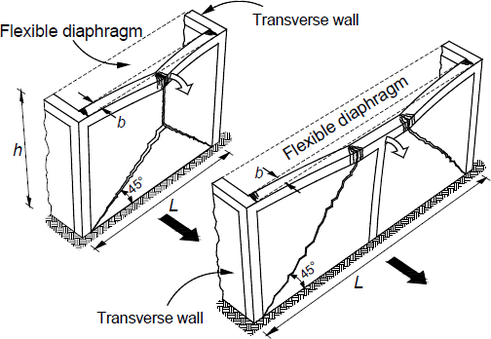
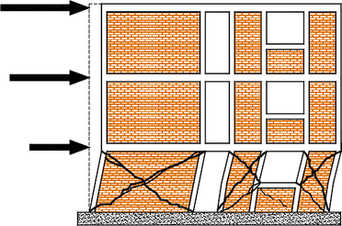
Obvykle pro seizmicky exponovanou a namáhanou konstrukci ze sevřeného zdiva není rozhodující samotné svislé zatížení (při trvalé návrhová situaci), ale jeho kombinace s vodorovným seizmickým zatížením (při seizmické návrhové situaci). Pokud po výšce nedochází ke změně průřezu stěny, potom v dolních podlažích je obvykle kritické porušení v rovině (smyková stěna), viz obr. 3a, ale v horních podlaží může rozhodovat zatížení vodorovnými setrvačnými silami příčně na rovinu zdiva, viz obr. 3b a 4. Je žádoucí, aby diafragmata byla tuhá, což požaduje i EC8_1G.
a)
b)
Obr. 4 Způsob porušení při příčném zatížení zdiva při seizmické návrhové situaci pro: a) tuhé diafragma; b) poddajné diafragma
První generace EC6_1G obsahuje jen zásady, nikoli aplikační pravidla. Návrh byl založen na stejných předpokladech, která platila pro nevyztužené i vyztužené zdivo s drobnými upřesněními.
Druhá generace EC6_2G zavádí aplikační pravidla přímo ve formě analytických vztahů pro sevřené zdivo. Přičemž obecné zásady jsou víceméně zachovány, případně upřesněny. Jako délka stěny se zde uvažuje vždy délka zdiva včetně svírajících prvků. Aplikační pravidla také dodržují zásadu, že pokud průběh tlakového normálového napětí zasahuje do zdiva i betonu, uvažuje se materiál s nižší pevností.
3.1 Ověření sevřených zděných stěn vystavených účinkům převážně svislého zatížení
Odolnost sevřeného zdiva na převážně svislé účinky nebyla v předchozím vydání EC6_1G a ve zde uvedených zásadách speciálně komentována, byla komentována společně s ohybem v rovině stěny. U nově zavedeného aplikačního pravidla v EC6_2G lze ovšem tvrdit, že splňuje zásady z předchozího vydání EC6_1G, tj. účinek tlačené výztuže se neuvažuje. V EC6_2G je také upřesněno, že délkou sevřeného zdiva se rozumí délka včetně svírajících prvků. Nové znění EC6_2G vyjadřuje odolnost pro svislé zatížení sevřeného zdiva ve tvaru
kde je
- Φ
- zmenšující součinitel v hlavě nebo v patě zahrnující vliv výstřednosti a štíhlosti stěny (viz čl. 8.2.2 EC6_2G),
- fd
- návrhová pevnost zdiva v tlaku (čl. 4.4.2 a 5.7.1),
- At
- průřezová plocha stěny včetně ztužujících prvků.
Podle Marques & Lourenço [4] je tento analytický vztah velmi konzervativní. U sevřeného zdiva nedojde při trvalé návrhové situaci ke zvýšení odolnosti stěny v tlaku oproti nevyztuženému zdivu. Ověření stěny na převážně svislé zatížení je tedy totožné jako u nevyztuženého zdiva.
3.2 Únosnost v ohybu v rovině stěny
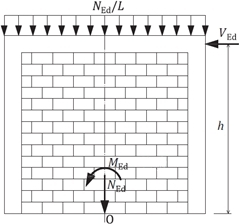
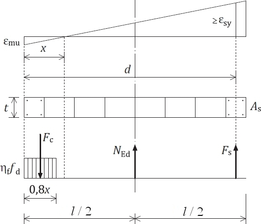
Únosnost v ohybu v rovině stěny dle EC6_2G je v souladu se zásadami uvedenými v předchozím vydání EC6_1G. Odolnost stěny v ohybu v rovině se stanovuje na základě předpokladů zobrazených na obr. 5. Předpokládá se, že je plně aktivována návrhová hodnota meze kluzu výztuže v tahu a že v tlaku působí obdélníkové tlakové napětí v betonu a zdivu, který je v souladu s ekvivalentním obdélníkovým pracovním diagramem (čl. 5.8.1). Pokud tlačená oblast zasahuje i do zdiva, potom se volí pevnost v tlaku podle méně pevnějšího materiálu. Výztuž v tlaku se nezapočítává do odolnosti průřezu.
a)
Obr. 5 Ohyb sevřeného zdiva v rovině zdiva: a) působící síly, b) poměrná deformace a vnitřní síly v průřezu (čl. 8.11)
Poloha neutrální osy v průřezu (souřadnice x) je odvozena z podmínky rovnováhy sil v průřezu zobrazených na obr. 5b, kterou lze zapsat ve tvaru
a potom ohybová odolnost sevřeného zdiva je
kde je
- As
- plocha podélné ocelové výztuže;
- fyd
- návrhová hodnota meze kluzu výztuže;
- l
- délka stěny;
- d
- vzdálenost mezi těžištěm tažené výztuže a nejvíce tlačeným vláknem průřezu, nebo účinná výška;
- x
- výška neutrální osy průřezu;
- ηf
- součinitel stanovující ekvivalentní obdélníkový obrazec průběhu napětí (čl. 5.8.1),
- fd
- návrhová hodnota pevnosti zdiva v tlaku (čl. 4.4.2 a 5.7.1).
Pokud je ale veliká hodnota svislého zatížení NEd , nemusí dojít k plnému aktivování fyd. Je třeba ověřit, že při dosažení εmu v tlaku platí
případně použít složitější (iterační) výpočet. Mezní poměrné přetvoření zdiva v tlaku se uvažuje εmu = 0,0035 pro zdicí prvky skupiny 1, které jsou ale jiné než z betonu s lehkým kamenivem a z autoklávovaného betonu, jinak se uvažuje hodnota εmu = 0,002 (čl. 5.8.1).
Součinitel stanovující ekvivalentní obdélníkový obrazec průběhu napětí ηf se uvažuje hodnotou ηf = 1,0 pro zdicí prvky skupiny 1, které jsou ale jiné než z betonu s lehkým kamenivem a z autoklávovaného betonu, jinak se uvažuje hodnota ηf = 0,85 (čl. 5.8.1).
Zařazení zdicích prvků do skupin obvykle provádí výrobce na základě požadavků uvedených v normě (čl. 5.1.2).
3.3 Smyková únosnost v rovině stěny
V zásadách předchozího vydání EC6_1G je uvedeno, že platí předpoklady jako pro nevyztužené zdivo a že délka tlačené oblasti průřezu ls se předpokládá jako délka zdiva. Nová generace EC6_2G místo ls zavádí ve vzorci pro smykovou odolnost účinnou výšku průřezu d, tj. vzdálenost těžiště výztuže ve svírajícím prvku táhlo-sloup k opačnému konci sevřené smykové stěny, viz obr. 5b. Jinak jsou předchozí zásady nezměněny. Postup je analogický k posouzení nevyztuženého zdiva. Vliv výztuže ve svislém ztužujícím prvku táhlo-sloup na smykovou únosnost stěny sevřeného zdiva se zanedbává.
Odolnost sevřeného zdiva na smykovou sílu v rovině stěny se dle EC6_2G stanoví z výrazu
kde je
- fvd
- návrhová pevnost zdiva ve smyku (čl. 4.4.2 a čl. 5.7.2), závislá na působení průměrného svislého tlakového napětí, působícího na stěnu vzdorující smyku;
- t
- tloušťka stěny vzdorující smyku; d účinná výška průřezu stěny (viz obr. 5b);
- VRdlt
- návrhová hodnota mezní smykové únosnosti;
- fd
- návrhová únosnost zdiva v tlaku ve svislém směru (čl. 4.4.2 a čl. 5.7.1).
Průměrné svislé tlakové napětí působící na stěnu vzdorující smyku, které je vstupním parametrem pro stanovení fvd , není v EC6_2G komentováno. Podle publikací týmu Marques et al. [4, 6] lze usuzovat, že průměrným svislým tlakovým napětím se rozumí
3.4 Ověřování zděných stěn vystavených ostatním zatěžovacím podmínkám
Ověřování stěn ze sevřeného zdiva vystavených ostatním zatěžovacím podmínkám je založeno na předpokladech pro nevyztužené zdivo (čl. 8.4 a čl. 8.5), přičemž se berou v úvahu ustanovení pro posuzování mezních stavů sevřeného zdiva (čl. 8.10.2 a čl. 8.10.3), pokud jsou použitelná.
Mezi ostatní zatěžovací podmínky se řadí zejména zatížení příčným zatížením na rovinu sevřeného zdiva při seizmické návrhové situaci, které může být rozhodující pro vyšší podlaží zděného objektu. Boční zatížení při seizmické návrhové situaci je třeba stanovit v souladu s předpoklady EC8.
4. Analýza konstrukce pro seizmickou návrhovou situaci
Při navrhování konstrukcí odolných proti zemětřesení je třeba vycházet z ustanovení v EC8. Druhá generace v době přípravy příspěvku nebyla uceleně publikována, resp. EN 1998-1-2, která bude obsahovat další požadavky na zděné konstrukce, zatím není schválena. Předpis EN 1998-1-1 je vzhledem k EC8_1G velmi přepracován, ale základní principy jsou zachovány. Přesto v souvislosti se sevřeným zdivem určeným převážně do seizmicky aktivních oblastí a dále uvedeným příkladem lze uvést alespoň několik velmi stručných poznámek vycházejících z EC8_1G.
- Není nutné provádět ověření konstrukce dle EC8, jestliže se jedná o velmi malou seizmicitu.
- Pokud je nutné ověřit konstrukci dle EC8, a jsou splněny podmínky pro „jednoduchou zděnou stavbu“ dle EC8, potom je možné prokázat spolehlivost splněním v normě daných konstrukčních podmínek a neposuzovat každý konstrukční prvek dle EC6.
- V případě nutnosti provést analýzu konstrukce, tak se vychází ze seizmické návrhové situace s odpovídajícími součiniteli spolehlivosti zatížení a součiniteli kombinace dle EC8. Svislé zatížení (stálé i proměnné) se převádí na ekvivalentní hmotu pro další dynamický výpočet nebo metodu příčných sil.
- Model konstrukce může být při splnění daných podmínek rovinný, anebo v některých případech je nutný prostorový.
- Pro vlastní analýzu je možné použít více metod, a to lineární (metoda výpočtu pomocí příčných sil nebo modální analýza pomocí spektra odezvy) i nelineární metody (nelineární výpočet metodou statického přitěžování nebo nelineární dynamický výpočet časového průběhu odezvy).
- Analytické vztahy pro sevřené zdivo jsou vyjádřeny pro vnitřní síly, tj. VEd, MEd, NEd, a proto v modelu bývá konstrukce nahrazena ekvivalentním rámem, kdy svislé výztužné prvky i zdivo je nahrazeno jedním svislým prutem.
- Pro maximální využití kapacity konstrukce lze doporučit použití nelineární inkrementální metody, kdy jsou vnitřní síly při dosažení podmínek plasticity v jednom konstrukčním prvku dále plasticky přerozděleny po konstrukci. Efektivní je tzv. „push-over“ analýza s využitím metody ekvivalentních rámů [8].
5. Příklad
5.1 Zadání
Úkolem je posoudit konstrukci ze sevřeného zdiva provedenou ze zdicích prvků Wienerberger Climamur [9, 10], a to v průřezu v úrovni terénu. Zdivo je provedeno z prvků Climamur 30 na Dryfix s dvěma pruhy, tloušťka zdiva je t = 300 mm. Předpokládejme, že konstrukci je možné řešit jako rovinnou a její tvar je zobrazen na obr. 6.
Zdicí prvky Climamur 30 mají v sortimentu zvláštní bloky se svislými otvory pro ztužující prvky sevřeného zdiva, svislé otvory mají rozměr 150 × 150 mm a osa otvoru (těžiště výztuže) je 150 mm od okraje zdiva, viz obr. 6. Ztužující prvek působící jako táhlo-sloup je vyztužen 4 pruty ⌀10 mm z oceli B500B.
Při seizmické návrhové situaci předpokládejme pro vysvětlení analytických vztahů pro sevřené zdivo zjednodušeně zatížení svislými a příčnými silami (Fxi,d a Fzi,d), jak je zobrazeno na obr. 6. Předpokládejme také, že analýzou konstrukce byly zjištěny reakce v úrovni terénu (VEd, MEd, NEd1 a NEd2), které jsou rovněž uvedeny na obr. 6.
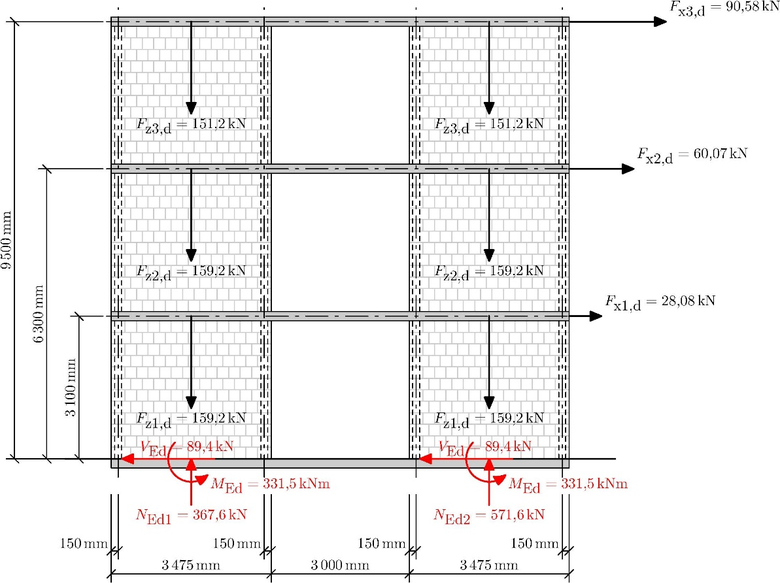
Obr. 6 Schéma rovinné konstrukce ze sevřeného zdiva s předpokládaným svislým a vodorovným zatížením při seizmické návrhové situaci (Fxi,d a Fzi,d) a reakcemi v úrovni terénu (VEd , MEd , NEd1 a NEd2)
V podkladech [9] jsou pro Climamur 30 na Dryfix se dvěma pruhy uvedeny následující materiálové parametry zdiva:
- normalizovaná průměrná pevnost v tlaku zdicího prvku fb = 7,5 MPa;
- charakteristická hodnota pevnosti zdiva v tlaku fk = 3,23 MPa;
- charakteristická hodnota počáteční pevnosti zdiva ve smyku bez zatížení tlakem fvko = 0,17 MPa;
- dílčí součinitel materiálu pro seizmickou návrhovou situaci γM = 1,67 (uvažuje se dle EC8_1G jako 2/3 hodnoty při trvalé návrhové situaci).
Obr. 7 Zdicí prvky Climamur 30: a) zdicí blok se svislým otvorem pro svírající prvek sevřeného zdiva působící jako táhlo-sloup [9]; b) rozměry a umístění svírajícího prvku táhlo-sloup ve zdivu provedeného z Climamur 30 [10]
5.2 Ostatní materiálové parametry
Z výše uvedeného lze stanovit další potřebné materiálové parametry pro posouzení konstrukce ze sevřeného zdiva:
- Při seizmické návrhové situaci se uvažuje dílčí součinitel materiálu pro ocel γs = 1,00. Proto lze uvažovat fyk = fyd = 500 MPa.
- Návrhová hodnota pevnosti zdiva v tlaku při seizmické návrhové situaci je fyd = fyk / γM = 3,32 / 1,67 = 1,94 MPa.
- Zdicí prvky Climamur 30 patří do skupiny 3 dle EC6_2G. Proto mezní poměrné přetvoření zdiva v tlaku se uvažuje εmu = 0,002 (čl. 5.8.1).
- Pro zdicí prvky skupiny 3 dle EC6_2G je součinitel stanovující ekvivalentní obdélníkový obrazec napětí ηf = 0,85 (čl. 5.8.1).
- Poměrné přetvoření výztuže na mezi kluzu εsy se určí z výrazu εsy = fyd / Es, kde se uvažuje Es = 200 GPa, viz čl. 3.2.7 v ČSN 1992-1-1 ed. 2 [11]. Hodnota poměrného přetvoření výztuže na mezi kluzu je proto εsy = 0,5 / 200 = 0,0025.
5.3 Geometrické parametry smykové stěny ze sevřeného zdiva
Ze zadání plynou také následující geometrické parametry pro posouzení stěny:
- tloušťka zdiva t = 300 mm;
- délka zdiva včetně ztužujících prvků l = 3 475 mm;
- účinná výška průřezu d = l − 150 mm = 3 475 − 150 = 3 325 mm;
- plocha výztuže pro 4 pruty ⌀10 mm je As = 314 mm2.
5.4 Únosnost v ohybu v rovině stěny
Pro stěnu vlevo je NEd1 = 367,6 kN a MEd = 331,5 kNm. Souřadnice neutrální osy se podle výrazu (1) určí následovně:
x = (367,6 + 314.10−6 × 500.103) / (0,8 × 0,85 × 1,94.103 × 0,3) = 1,326 m (7)
Ověření poměrné deformace v tažené výztuži dle výrazu (4):
εs = 0,002 × (3,325 − 1,326) / 1,326
εs = 0,0031 > εsy = 0,0025 (8)
V tažené výztuži je aktivováno napětí fyd.
Únosnost v ohybu pro stěnu vlevo je potom v souladu s výrazem (3):
MRd = 314.10−6 × 500.103 (3,325 − 0,4 × 1,326) + 367,6 (0,5 × 3,475 − 0,4 × 1,326)
MRd = 882,3 kNm > MEd = 331,5 kNm (9)
Průřez VYHOJUJE.
Pro stěnu vpravo jsou účinky zatížení NEd2 = 571,6 kN a MEd = 331,5 kNm. Poloha neutrální osy v průřezu se potom vypočte:
x = (571,6 + 314.10−6 × 500.103) / (0,8 × 0,85 × 1,94.103 × 0,3) = 1,841 m (10)
Ověření poměrné deformace v tažené výztuži:
εs = 0,002 × (3,325 − 1,841) / 1,841
εs = 0,00162 < εsy = 0,0025 (11)
V tažené výztuži není aktivováno napětí fyd!
Napětí ve výztuži lze odhadnout hodnotou σs(1) = fyd εs / εsy , což je první odhad do složitějšího iteračního výpočtu, kdy souřadnici N.O. je třeba znovu přepočítat opakováním výpočtu od výrazu (10) s napětím σs(1) místo fyd a určit zpřesněný nový odhad σs(i). Výsledky iteračního výpočtu jsou uvedeny v tab. 1, kde je patrná konvergence již při malém počtu iterací.
| i | σs(i) [MPa] | x(i) [m] |
|---|---|---|
| 1 | 321,6 | 1,701 |
| 2 | 381,7 | 1,749 |
| 3 | 360,4 | 1,732 |
| 4 | 367,8 | 1,738 |
| 5 | 365,2 | 1,736 |
| 6 | 366,1 | 1,737 |
Únosnost v ohybu pro stěnu vpravo je potom spočtena s napětím ve výztuži σs = 366,1 MPa a souřadnicí neutrální osy x = 1,737 m následujícím postupem:
MRd = 314.10−6 × 366,1.103 (3,325 − 0,4 × 1,737) + 571,6 (0,5 × 3,475 − 0,4 × 1,737)
MRd = 898,3 kNm > MEd = 331,5 kNm (12)
Průřez VYHOJUJE.
5.5 Smyková únosnost v rovině stěny
Pro stěnu vlevo je VEd = 89,4 kN a NEd1 = 367,6 kN. Průměrné normálové napětí ve stěně, viz výraz (6), se určí ze vztahu:
Potom charakteristická hodnota pevnosti zdiva ve smyku fvk je dána výrazem (viz čl. 5.5), kde charakteristická hodnota součinitele tření µf je uvažována hodnotou 0,4 (čl. 5.7.2.3). Pevnost fvk nemá být uvažována větší než 0,065 fb.
fvk = 0,17 + 0,4 × 0,353 = 0,311 MPa < 0,065 fb = 0,488 MPa (14)
Návrhová hodnota pevnosti zdiva ve smyku fvd :
Smyková únosnost v rovině se má uvažovat nejvýše hodnotou VRdlt
Smyková únosnost v rovině VRd je dána vztahem
VRd = 0,187.103 × 0,3 × 3,325 = 186,5 kN < VRdlt = 580 kN
VRd = 186,5 kN > VEd = 89,4 kN (17)
Průřez VYHOJUJE.
Pro stěnu vpravo je VEd = 89,4 kN a NEd2 = 571,6 kN. Průměrné normálové napětí ve stěně je:
Potom charakteristická hodnota pevnosti zdiva ve smyku fvk :
fvk = 0,17 + 0,4 × 0,548 = 0,389 MPa < 0,065 fb = 0,488 MPa (19)
Návrhová hodnota pevnosti zdiva ve smyku fvd :
Smyková únosnost v rovině VRd je dána vztahem
VRd = 0,234.103 × 0,3 × 3,325 = 233,4 kN < VRdlt = 580 kN
VRd = 233,4 kN > VEd = 89,4 kN (21)
Průřez VYHOJUJE.
5.6 Posouzení v ostatních průřezech
Analytické vztahy odolnosti průřezu pro sevřené zdivo uvedené v EC_2G byly výše uvedeným příkladem jistě dostatečně vysvětleny. Obdobně je ale nutné posoudit také všechny ostatní průřezy i ve vyšších úrovních. Svislé zatížení se s počtem podlaží směrem nahoru mění přibližně lineárně, ale příčné síly nikoli. Rozhodující průřez proto nemusí být ten v úrovni terénu.
6. Závěr
Lze shrnout, že změny v oblasti sevřeného zdiva spočívají zejména v definování analytických modelů pro ověření sevřeného zdiva, a to pro následující případy namáhání sevřeného zdiva:
- zatíženého převážně svislým zatížením,
- zatíženého ohybem v rovině stěny a
- smykem v rovině stěny.
Tato nová aplikační pravidla většinou respektují zásady v předchozí generaci EC6_1G, resp. změny oproti předchozím zásadám jsou malé.
Metoda ověření sevřeného zdiva zatíženého převážně svislým zatížením je identická s ověřováním nevyztuženého zdiva. Pro tento případ se délka zdiva uvažuje včetně ztužujících prvků a pevnost se uvažuje toho méně pevného materiálu, tj. obvykle pevnost zdiva. Nedochází tedy při trvalé návrhové situaci ke zvýšení únosnosti na převážně svislé zatížení vlivem provedení ztužujících prvků táhlo-sloup a táhlo-trám. Proto sevřené zdivo nachází uplatnění zejména v seizmicky aktivních oblastech, kde se posuzuje konstrukce při seizmické návrhové situaci.
Analytické vztahy pro sevřené zdivo uvedené v EC6_2G je ovšem třeba chápat v kontextu skutečného chování konstrukce jako zjednodušující. Publikace týmu Marques at al. [4, 5, 6] i další publikace např. na portále Confined Masonry Network [3] ukazují, že skutečné rozdělení svislého normálového napětí v patě sevřeného zdiva u smykové stěny při seizmické návrhové situaci není rovnoměrné, ale spíše trojúhelníkové. Proto analytické vztahy užívané v jiných částech světa vycházejí často z odlišných předpokladů a jsou odlišně formulovány než v EC6.
Je třeba také upozornit, že EC8_1G pro navrhování konstrukcí odolných proti zemětřesení uvádí další požadavky, a to mnohdy přísnější, než jsou v EC6_2G. Pro seizmicky aktivní oblasti je nutné ověřit aktuální požadavky dle nově připravovaného předpisu EC8_2G.
7. Literatura
- ČSN EN 1996-1-1:2024 Eurokód 6: Navrhování zděných konstrukcí – Část 1-1: Obecná pravidla pro vyztužené a nevyztužené zděné konstrukce. ÚNMZ, Praha, 2024.
- ČSN EN 1996-1-1+A1:2013 Eurokód 6: Navrhování zděných konstrukcí – Část 1-1: Obecná pravidla pro vyztužené a nevyztužené zděné konstrukce. Praha: ÚNMZ, 2013.
- Confined Masonry Network | Promoting seismically safe, economical housing worldwide. Online. 2018. Dostupné z: https://confinedmasonry.org/. [cit. 2024-03-18]
- Marques, R., Lourenço, P.B. Structural behaviour and design rules of confined masonry walls: Review and proposals. Construction & building materials. 2019, Vol. 217, pp. 137–155.
- Marques, R., Lourenço, P.B. A model for pushover analysis of confined masonry structures: implementation and validation. Bull Earthquake Eng 11, 2133–2150 (2013).
- Rui Marques, João M. Pereira, Paulo B. Lourenço. Lateral in-plane seismic response of confined masonry walls: From numerical to backbone models. Engineering Structures. Volume 221, 2020, p. 111098, ISSN 0141-0296.
- ČSN EN 1998-1 ed. 2:2013 Eurokód 8: Navrhování konstrukcí odolných proti zemětřesení – Část 1: Obecná pravidla, seizmická zatížení a pravidla pro pozemní stavby. Praha: ÚNMZ, 2013.
- Magenes, Guido. A method for pushover analysis in seismic assessment of masonry buildings. The 12th WCEE conferece, 2000.
- Wienerberger S.A.S. Climamur un nouvel art de vivre. Documentation technique. Dostupné z: https://www.climamur.fr/. [cit. 2024-03-26]
- Wienerberger S.A.S. Guide de mise en oeuvre, Briques de mur Porotherm Climamur. Dostupné z:
https://www.climamur.fr/. [cit. 2024-03-26] - ČSN 1992-1-1 ed. 2:2019 Eurokód 2: Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby. Praha: ÚNMZ, 2019.
![Obr. 7 Zdicí prvky Climamur 30: a) zdicí blok se svislým otvorem pro svírající prvek sevřeného zdiva působící jako táhlo-sloup [9]](/docu/clanky/0294/029499o19.png)
![Obr. 7 Zdicí prvky Climamur 30: b) rozměry a umístění svírajícího prvku táhlo-sloup ve zdivu provedeného z Climamur 30 [10]](/docu/clanky/0294/029499o21.png)