Vybrané grafické metody zjišťování činitele denní osvětlenosti (1. část)
Článek se zabývá popisem vybraných graficko-početních metod sloužících ke stanovení množství denního světla. Je vysvětlen princip odvození těchto metod a popsán princip práce s příslušnými diagramy. V současné době se zřídka setkáváme s používáním diagramů v praxi, ale některé odborné softwary je využívají buď přímo, nebo alespoň ve svých grafických výstupech.
1. Definice činitele denní osvětlenosti
Obloha je plošným zdrojem světla, který se vyznačuje velkou proměnlivostí v čase s nemožností předpovědět jeho stav i jen na několik minut málo dopředu. Proto byl jako kritérium denního osvětlení v československých technických normách zaveden činitel denní osvětlenosti D (%) [1], neboť se jedná o veličinu, jejíž hodnoty jsou stálejší než hodnoty samotné osvětlenosti E (lx). Činitel denní osvětlenosti je definován jako podíl osvětlenosti E (lx) daného místa k osvětlenosti Eh (lx) vodorovné ničím nestíněné roviny. Veličina Eh (lx) je tedy osvětleností vodorovné roviny celou oblohou. Musí být změřena ve stejném okamžiku jako E (lx).
Avšak i takto definované kritérium zůstává velmi nestálé, protože rozložení jasu L (cd‧m−2) po obloze je rovněž velmi proměnlivé. Pro účely hodnocení musí být rozložení jasu normováno. Mezinárodní komise pro osvětlování CIE rozeznává 15 základních typů obloh [2]. Z nich byly v naší normalizaci použity dvě: obloha s konstantním jasem definovaná už v 18. století Lambertem [3] a od roku 1968 [4] byla i u nás zavedena obloha s gradovaným jasem podle CIE-E 3.2. (1955) [19] inspirovaná výzkumem Moona a Spencerové [5]. Tato obloha se vyznačuje gradací jasu v závislosti na výškovém úhlu ε (°) nad horizontem podle vztahu
kde q (–) je činitel gradovaného jasu, Lm (cd‧m−2) je průměrný jas oblohy, Lε (cd‧m−2) je jas sledovaného místa na obloze, jehož poloha je určena úhlem ε (°) nad horizontem.
Z uvedeného vztahu plyne, že tento model oblohy není závislý na poloze slunce na obloze. Jedná se o model rovnoměrně zatažené oblohy v zimě při tmavém terénu. Logika posuzování spočívá ve skutečnosti, že daný model oblohy představuje tu nejméně příznivou variantu rozložení jasu, a proto všechny hodnoty osvětlenosti během roku budou vyšší (příznivější) než hodnota podle tohoto modelu vypočtená. Z uvedeného vztahu také plyne, že jas zatažené oblohy je 3× větší v zenitu oproti jasu na horizontu, proto se tento model označuje jako CIE 1:3. Zároveň platí, že
Činitel denní osvětlenosti stanovený na tomto modelu oblohy se zachoval jako kritérium denního osvětlení téměř až do dnešních dnů. Změnu přinesla až nová evropská norma, kterou naše republika převzala v roce 2019 [6]. Tato norma uvádí kritéria ve třech úrovních – nízká, střední a vysoká. Pro nízkou úroveň je jako kritérium stanovena cílová osvětlenost ET = 300 lx, která musí být zajištěna na minimálně 50 % plochy místnosti nebo její funkčně vymezené části a minimální cílová osvětlenost ETM = 100 lx, která musí být zajištěna na 95 % plochy místnosti nebo její funkčně vymezené části. Výpočet hodnot cílových osvětleností je založen na výpočtu osvětlenosti daného místa v interiéru budovy, při kterém se stanovují hodnoty činitele denní osvětlenosti jednou ze dvou možností – 1) při rovnoměrně zatažené obloze v zimě nebo 2) v hodinovém nebo kratším intervalu v běžném roce při oblohových a slunečních podmínkách vycházejících z klimatických údajů pro dané místo. Jedná se tak o statistické zpracování nejméně 365 × 12 = 4380 údajů. Podle zeměpisné polohy byly jednotlivým zemím, resp. jejich hlavním městům, přiděleny hodnoty mediánu oblohové vodorovné osvětlenosti Ev,d,med (lx). Praze byla přidělena hodnota Ev,d,med = 14900 lx. Vypočtené, změřené nebo limitní (požadované pro splnění požadavků) hodnoty cílového činitele denní osvětlenosti DT (%) resp. DTM (%) se stanoví podle vztahů
I podle evropské normy tak můžeme k hodnocení použít činitel denní osvětlenosti stanovený za stavu rovnoměrně zatažené oblohy v zimě při tmavém terénu (model oblohy CIE 1:3), pouze se změnily nejnižší požadované hodnoty a způsob jejich uplatňování. V kontextu evropské normy se o množství denního světla hovoří jako o příspěvku denního osvětlení.
2. Fotometrie činitele denní osvětlenosti
Hodnotu činitele denní osvětlenosti je možno stanovit pomocí základních vztahů fotometrie pro plošný zdroj světla nebo pomocí některé z grafických pomůcek, které byly v minulosti vyvinuty, nebo s pomocí specializovaného softwaru. Základní vztahy fotometrie dokumentuje obrázek 1, který znázorňuje dvojí průmět plochy okna. Okno o ploše S (m2), kterým přichází denní světlo z oblohy, se promítne z posuzovaného bodu P (na obrázku na podlaze místnosti) na myšlenou polokulovou plochu (hemisféru) o poloměru R do plochy S1 (m2) – viz červená plocha na obrázku. Tato plocha se pak kolmo svisle (ortogonálně) promítne do podstavy hemisféry jako plocha S2 (m2) – viz zelená plocha na obrázku. Osvětlenost E (lx) v bodě P lze pak stanovit podle vztahu
kde L (cd‧m−2) je jas oblohy.
Při použití jednotkového poloměru R = 1 hemisféry se vztah (6) zjednoduší, jak uvedeno v jeho pravé části. Osvětlenost Eh (lx) vodorovné ničím nestíněné roviny je dána vztahem (7).
Při jednotkovém poloměru hemisféry R = 1 lze hodnotu činitele denní osvětlenosti stanovit v závislosti na ploše S2 (m2) zohledněním rovnic (3) a (6) ve vzorci (1).
Vztah platí jen pro oblohu s konstantním jasem. Je-li jas oblohy proměnný, pak je nutno hemisféru rozdělit na velké množství dílčích ploch Sj1 (m2) a výpočet dílčího činitele denní osvětlenosti Dj (%) provést pro každou plochu odděleně podle vztahu
kde Lj (cd‧m−2) je jas dílčí plochy a qj (–) její činitel jasu. Výsledná hodnota činitele denní osvětlenosti se získá jako součet
kde n je počet dílčích ploch. Hodnoty Sj2 (m2) byly stanoveny za předpokladu, že R = 1.
3. Daniljukovy úhlové sítě
Mezi grafickými pomůckami používanými ke stanovení činitele denní osvětlenosti u nás největšího rozšíření a obliby doznaly Daniljukovy úhlové sítě [7]. Metoda využívá dvě grafické pomůcky – Daniljukovy úhlové sítě (diagramy). Jedna z pomůcek se používá při práci v řezu a druhá při práci v půdorysu osvětlované místnosti.
Hemisféra se středem v osvětlovaném místě nad osvětlovanou rovinou je ve dvou na sebe kolmých směrech těmito sítěmi rozdělena v každém směru na 100 dílků. Tím je obloha rozdělena na 10 000 plošek, z nichž každá v osvětlovaném místě vyvolá stejnou osvětlenost ΔE = Eh·10−4 (lx). Každá z uvedených plošek tedy přispěje ve sledovaném místě hodnotou činitele denní osvětlenosti ΔD = 0,01 %. Metoda vychází z modelu zatažené oblohy s konstantním jasem, tj. každá ploška oblohy má stejný jas, a neuvažuje ztráty světla v osvětlovacím otvoru. Proto musí být při výpočtu korigována činitelem gradovaného jasu q (–) a souhrnným činitelem prostupu světla τ0,ψ (–). Výhodou je možnost univerzálního použití metody pro různé sklony a tvary osvětlovacích otvorů, různé sklony osvětlovaných rovin i pro případné různé modely oblohy. Funkční vyobrazení Daniljukových úhlových sítí i s návodem k použití a s řešenými příklady lze nalézt v publikaci [8]. V tomto článku jsou reprodukovány sítě z původní Daniljukovy práce [7].
Kromě grafické práce je možno Daniljukovu metodu použít i k přímému výpočtu s použitím algoritmů, podle kterých byly úhlové sítě sestrojeny [9]. Diagram pro řez vychází z dělení hemisféry svazkem rovin s průsečnicí, která leží v osvětlované rovině a je rovnoběžná s rovinou osvětlovacího otvoru. Toto dělení připomíná způsob krájení melounu, jak je zřejmé z obrázku 4. Půdorysným průmětem kružnic na hemisféře jsou elipsy. Na vyobrazení je hemisféra o jednotkovém poloměru R = 1. Vše je uspořádáno tak, že plošný obsah útvaru vzniklého jako půdorysný průmět dvou sousedních kružnic úhlové sítě je vždy jednou setinou plochy S0 = π (m2) kruhu, který je průmětem celé hemisféry. Plocha Sa (m2) souvisí s elevačním úhlem ε (°) a je vyznačena tečkováním. Tuto plochu lze stanovit jako polovinu rozdílu plochy celého kruhu a plochy příslušné elipsy s vedlejší poloosou a = cos ε.
Ploše S0 = π odpovídá 100 dílků úhlové sítě pro řez. Vztah mezi elevačním úhlem ε (°) a číslem n1 dílku úhlové sítě pro řez plyne z úměrnosti ploch n1 / 100 = Sa / S0
Diagram pro půdorys vychází z rozdělení hemisféry soustavou svislých rovnoběžných rovin kolmých na rovinu osvětlovacího otvoru. Toto dělení připomíná způsob, jakým se krájí chléb, jak je patrné z obrázku 4. Půdorysným průmětem kružnic na hemisféře jsou úsečky, které vymezují plochy kruhových úsečí. Plocha Sb (m2) kruhového pásu vyznačeného ve vyobrazení šrafováním na obrázku souvisí s azimutálním odklonem α (°) od kolmice k osvětlovacímu otvoru v Daniljukově úhlové síti pro půdorys.
Vztah mezi azimutálním odklonem α (°) a číslem n2 dílku úhlové sítě pro půdorys plyne z úměrnosti ploch n2 / 100 = Sb / S0.
3.1 Specifika při délkově omezené stínící překážce
Činitel denní osvětlenosti D (%) se získá součtem tří jeho dílčích složek – oblohové Ds (%), vnější odražené De (%) a vnitřní odražené Di (%). Text tohoto článku se zabývá způsoby stanovení prvních dvou dílčích složek činitele denní osvětlenosti.
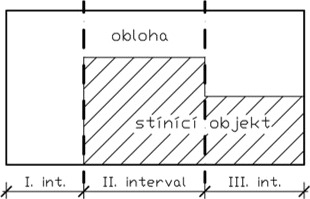
Obrázek 5: Ukázka rozdělení vlivu světla v dílčích intervalech
Maximální rozsah dopadu světla vymezený zboku ostěním osvětlovacího otvoru, shora nadpražím a zespodu parapetem (je-li výš než srovnávací rovina) nebo srovnávací rovinou (je-li výš než parapet) je nutné rozčlenit na dílčí intervaly tak, aby v daném intervalu byla z kontrolního bodu vidět přes celou výšku osvětlovacího otvoru:
- pouze obloha → De = 0 %,
- pouze stínící objekt → Ds = 0 %,
- obloha a stínící překážka konstantní výšky → viz postup dále (v případě, že je objekt proměnlivé výšky je třeba uzpůsobit počet intervalů).
Oblohová a vnější odražená složka se vypočítá součtem dílčích složek z daných m-intervalů.
3.2 Stanovení oblohové a vnější odražené složky činitele denní osvětlenosti
Pomocí Daniljukových úhlových sítí lze stanovit dvě ze tří složek činitele denní osvětlenosti s využitím příslušných výpočtových vztahů.
- oblohová složka:
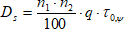 (17)
(17)
- vnější odražená složka:
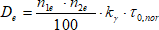 (18)
(18)
Zatímco určení některých veličin je shodné pro grafickou i početní metodu, jiné se stanovují odlišně. Pro přehlednost jsou proto tyto postupy uvedeny v následující tabulce.
| Označení a název dílčí veličiny | Postup | ||
|---|---|---|---|
| Graficko-početní | Pouze početní | ||
| Stanovení dílčí veličiny (číslo rovnice) | |||
| n1 | počet dílků v diagramu, které zaujímá oblohová / vnější odražená složka v řezu | odečtem z Daniljukovy úhlové sítě pro řez |
|
| n1e |
| ||
| β1 (°) β2 (°) β3 (°) | úhel mezi srovnávací rovinou a … (viz obrázek 6) | 1 – nadpražím 2 – spojnicí kontrolního bodu s horní hranou stínící překážky 3 – parapetem nebo srovnávací rovinou (tím, co je výše) | |
| q (–) | činitel gradovaného jasu pro zataženou oblohu v zimě |
|
|
| ε (°) | elevační úhel (mezi vodorovnou rovinou a těžišťovou osou oblohové složky) | úhloměrem (těžišťová osa pomocí Daniljukovy úhlové sítě pro řez) |
|
| kγ (–) | činitel jasu stínící překážky |
obvykle se uvažuje kγ = 0,1; přesně | |
| Lε (cd.m−2) | jas oblohy v úhlu ε (°) nad horizontem | ||
| Lm (cd.m−2) | průměrný jas oblohy | ||
| τ0,ψ (–) | souhrnný činitel propustnosti světla |
| |
| τs (–) | činitel prostupu světla sklem nebo jiným světlo propustným materiálem | přímo hodnota τs od výrobce nebo součin hodnot τs, nor | |
| τk (–) | činitel prostupu světla zohledňující vliv konstrukcí osvětlovacího otvoru nepropouštějících světlo |
| |
| As (m2) | část plochy osvětlovacího otvoru propouštějící světlo | ||
| Ac (m2) | celková plocha osvětlovacího otvoru | ||
| τz (–) | činitel znečištění |
| |
| τz,e (–) | činitel znečištění na vnější straně otvoru | tabulková hodnota v závislosti na sklonu osvětlovacího otvoru a stupně znečištění vzduchu (např. dle [10]) | |
| τz,i (–) | činitel znečištění na vnitřní straně otvoru | ||
| τψ (–) | činitel prostupu světla sklem ve směru úhlu ψ měřeném od normály roviny skla |
|
|
| ψ (°) | úhel mezi normálou zasklení a těžišťovou osou oblohové složky (směr prostupu světla) | úhloměrem (normála = kolmice na danou rovinu) | pouze pro svislý osvětlovací otvor platí ε = ψ |
| τb (–) | činitel prostupu světla zohledňující vliv stínění konstrukcemi budovy | tabulková hodnota v závislosti na typu stínící konstrukce (např. dle [10]) | |
| τc (–) | činitel prostupu světla zohledňující vliv zařízení pro regulaci osvětlení |
| |
| Ac-r (m2) | plocha osvětlovacího otvoru, kterou kolmo prostupuje světlo (plocha otvoru – plocha zařízení pro regulaci světla) | ||
| τ0, nor (–) | souhrnný činitel prostupu světla ve směru normály |
| |
Při početním určení počtu dílků obou složek v půdorysu je třeba nejprve z půdorysu místnosti zjistit následující vzdálenosti (obr. 6):
- vzdálenost m (mm) mezi kontrolním bodem a rovinou vnitřního zasklení osvětlovacího otvoru, v daném měřítku pomocí pravítka nebo jako skutečná hodnota,
- vzdálenosti a1 (mm) a a2 (mm) – mezi oběma ostěními osvětlovacího otvoru a normálou zasklení, která prochází kontrolním bodem, hodnoty musí být ve stejných jednotkách a měřítku jako hodnota m (mm).
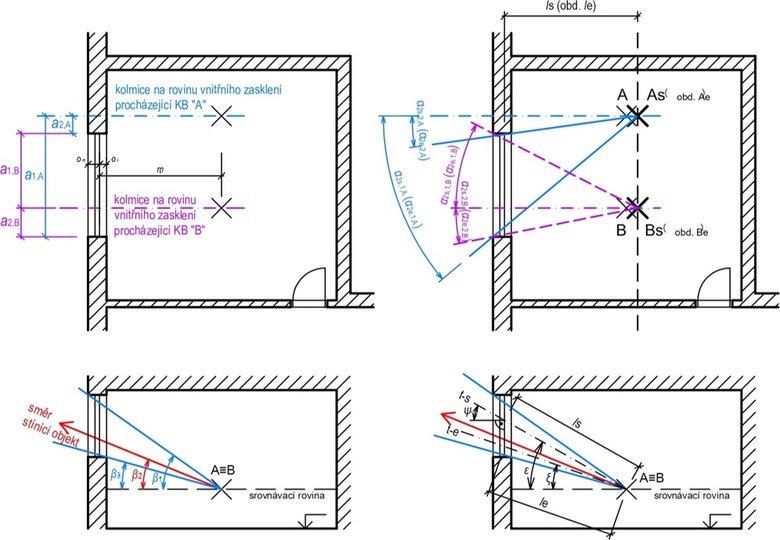
Obrázek 6: Schéma místnosti v půdorysu (nahoře) a ve svislém řezu (dole) včetně vyznačení vstupních údajů (vlevo) a těch dopočtených (vpravo)
Stanovení počtu dílků Daniljukovy úhlové sítě pro obě složky Ds (%) a De (%) je závislé na charakteru zástavby (při pohledu z kontrolního bodu) a na počtu osvětlovacích otvorů v místnosti. Rozumí se tím, zda se jeví překážka jako průběžná či nikoliv. Pro průběžnou překážku a pro místnost s jedním osvětlovacím otvorem se stanoví počet dílků pouze ve dvou intervalech, které jsou závislé na poloze ostění osvětlovacího otvoru vůči kontrolnímu bodu.
Počet dílků diagramu, kterou zaujímá oblohová složka v půdorysu se určí buď odečtem z Daniljukovy úhlové sítě pro půdorys nebo početně.
Počet dílků diagramu pro vnější odraženou složku v půdorysu se také určí buď odečtem z Daniljukovy úhlové sítě pro půdorys nebo početně.
Ve vzorcích (30) a (31) se znaménko „+“ použije v případě, kdy kolmice na rovinu zasklení (normála) procházející kontrolním bodem prochází přímo osvětlovacím otvorem (viz obr. 6 – fialově). V opačném případě se použije znaménko „−“ (na obrázku 6 modře), přičemž index 1 odpovídá většímu počtu dílků. V následujících výpočtových vztazích značí index i číslo odpovídajícího intervalu (1 nebo 2 podle značení vzdáleností a a tomu odpovídajících úhlů α). Ve vztazích (32) a (33) se index 1 použije pro větší ze vzdáleností a. Při výpočtu musí být zapnut mód RAD, přičemž některé PC softwary ho mají přednastaven.
Počet dílků oblohové složky v půdorysu odpovídající krajním mezím výseče možného dopadu světla se vypočte podle vztahu
Počet dílků vnější odražené složky v půdorysu odpovídající krajním mezím výseče možného dopadu světla se vypočte podle vztahu
Výpočet vstupních hodnot pro oba výše vztahy je uveden v tab. 2.
| Podmínka pro použití výpočtového vztahu | Výpočtový vztah |
|---|---|
| Normála zasklení procházející kontrolním bodem prochází přímo osvětlovacím otvorem – výpočet odklonů obou ostění (1 a 2) od normály: |
|
| Normála zasklení procházející kontrolním bodem leží mimo osvětlovací otvor – pouze pro větší ze vzdáleností ais a větší ze vzdáleností aie | |
| Normála zasklení procházející kontrolním bodem leží mimo osvětlovací otvor – pouze pro menší ze vzdáleností ais a menší ze vzdáleností aie |
|
| Poznámka k tab. 2: Vzdálenosti oe a oi jsou znázorněny na obrázku 6. Všechny délkové rozměry dosazované do uvedených vztahů musí být ve stejných jednotkách a stejném měřítku. | |
Vzdálenosti ls a le zohledňují délku těžišťové osy oblohové či vnější odražené složky činitele denní osvětlenosti mezi kontrolním bodem a průsečíkem dané těžišťové osy s rovinou vnitřního zasklení. Stanoví se pomocí již stanovených hodnot.
kde vzdálenost m je patrná z obrázku 6 vlevo nahoře, cos ε viz (22) a úhel ξ (°) vyjadřuje odklon těžišťové osy vnější odražené složky od vodorovné roviny a určí se jako:
6. Literatura
- ČSN 73 0511 Denní osvětlení průmyslových budov (1956).
- CIE 215:2014 CIE Standard General Sky Guide (2014).
- LAMBERT, J. H. Photometria sive de mensura et gradibus luminis, colorum et umbrae. Augsburg: Detlefsen, 1760.
- ČSN 36 0035 Denní osvětlení budov (1968).
- MOON, P. – SPENCER, D. E. Illumination from a non – uniform sky. Illuminating Engineering, 1942, (37)10, 707–726.
- ČSN EN 17037 Denní osvětlení budov (2019).
- DANILJUK, A. M. Diagramy dla raščota osveščenosti ot svetoprojomov proizvolnogo očertanija i naklona. Svetlotechnika, 1935, (6)6, 7–9.
- VYCHYTIL, J: Stavební světelná technika – cvičení. ČVUT Praha, 2015, 156 s., ISBN 978-80-01-05858-9.
- KAŇKA, J. Inovovaný způsob použití Daniljukovy metody. Světlo, 2011, (14)4, 44–46.
- VYCHYTIL, J. – KAŇKA, J.: Stavební světelná technika – přednášky. ČVUT Praha, 176 s., 2016, ISBN 978-80-01-06060-5.
- WALDRAM, P. J. A measuring diagram for daylight illumination. London: B. T. Batsford Ltd., 1950, 19 s.
- HALAHYJA, M. a kol: Stavebná tepelná technika, akustika a osvetlenie, Alfa Bratislava 1985.
- KAŇKA, J. Použití Waldramova diagramu při stanovení činitele denní osvětlenosti. Stavební obzor, 1993, (2)6, 157–159.
- ČSN 73 0580 Denní osvětlení budov – základní požadavky (2007)
- KAŇKA, J. Stanovení činitele denní osvětlenosti svislé roviny okna Waldramovým diagramem upraveným v ČVUT Praha. Světlo, 2002, (5)1, 18–19.
- KAŇKA, J: Vybrané stati ze stavební světelné techniky, ČVUT Praha 2014
- KAŇKA, J. – PELECH, M. Program pro výpočet činitele denní osvětlenosti WAL 1.1. Projektování a výstavba, 1995, 1–2, 39–43.
- Archiv firmy Osvětlení Oslunění Akustika – Ing. Jan Kaňka (IČ: 13158686)
- CIE-E 3.2. Official recommendation CIE-E 3.2: Natural daylight. Proc. CIE Zürich, II, 3.1., 1955.
The article deals with the description of selected graphic-numerical methods used to determine the amount of daylight. The principle of derivation of these methods is explained and the principle of working with the relevant diagrams is described. Nowadays, we rarely see the use of diagrams in practice, but some professional software uses them either directly or at least in their graphical outputs.
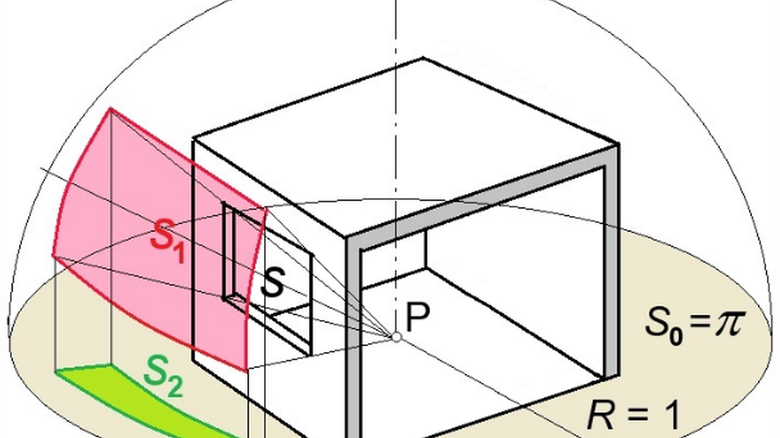
![Obrázek 1: K fotometrii plošného zdroje světla (podle [1])](/docu/clanky/0263/026320o9.png)
![Obrázek 2: Daniljukova úhlová síť pro řez (podle [7])](/docu/clanky/0263/026320o15.png)
![Obrázek 3: Daniljukova úhlová síť pro půdorys (podle [7])](/docu/clanky/0263/026320o17.png)
![Obrázek 4: Schéma konstrukce Daniljukových diagramů (podle [9])](/docu/clanky/0263/026320o19.png)