Anizotropní tepelná vodivost zdiva z dutinových tvarovek
Keramické tvarovky s vertikální orientovanými dutinami patří k velmi často používaným stavebním materiálům. Výrobci pro ně standardně uvádějí pouze ekvivalentní tepelné vodivosti ve vodorovném směru kolmo na povrch stěny, což ve většině běžných případů postačuje, protože tepelný tok přes zdivo je obvykle orientován právě takto.
Při posuzování řady tepelných vazeb (např. atik, založení stěn, ale i běžných rohů) je nicméně potřebné znát i ekvivalentní tepelné vodivosti zdiva ve zbylých dvou směrech, protože k šíření tepla dochází i ve svislém směru a ve směru rovnoběžném s povrchem stěny. Článek byl převzat ze sborníku konference Tepelná ochrana budov 2011 a pro server TZB info mírně rozšířen.
Příspěvek je zaměřen na rozdíly mezi ekvivalentní tepelnou vodivostí zdiva z keramických tvarovek o různém počtu dutin ve svislém a v obou vodorovných směrech. I když výrobci zdiva uvádějí v zásadě výhradně vlastnosti pro vodorovný tepelný tok (kolmo na povrch zdiva), při praktickém posuzování stavebních detailů je velmi často potřebné zohlednit skutečnost, že zdivo není izotropní materiál a jeho ekvivalentní tepelná vodivost je různá pro zbývající dva směry tepelného toku. V nedávné době byly publikovány nové studie, které s pomocí CFD modelování upřesnily vzájemný poměr tepelné vodivosti ve svislém a vodorovném směru (kolmo na povrch zdiva). V tomto příspěvku bude doplněn vztah mezi oběma tepelnými vodivostmi zdiva ve vodorovném směru a ukázány některé praktické důsledky upřesnění tepelných vlastností zdiva.
Úvodem
Keramické tvarovky s vertikálně orientovanými dutinami patří k velmi často používaným stavebním materiálům. Výrobci pro ně standardně uvádějí pouze ekvivalentní tepelné vodivosti ve vodorovném směru kolmo na povrch stěny, což ve většině běžných případů postačuje, protože tepelný tok přes zdivo je obvykle orientován právě takto. Při posuzování řady tepelných vazeb (např. atik, založení stěn, ale i běžných rohů) je nicméně potřebné znát i ekvivalentní tepelné vodivosti zdiva ve zbylých dvou směrech, protože k šíření tepla dochází i ve svislém směru a ve směru rovnoběžném s povrchem stěny. Uvažuje-li se tepelná vodivost zdiva shodná ve všech směrech, mohou výsledky posouzení podobných detailů vykazovat citelné chyby. Struktura dutinových tvarovek je totiž optimalizována pro šíření tepla kolmo k povrchu stěny a zdivo proto vykazuje ve zbylých směrech obvykle horší tepelné vlastnosti. Příčinou jsou sice především přímo probíhající stěny voštin, ale svou roli sehrává i konvekce ve větších svislých vzduchových dutinách.
Problematikou komplexního šíření tepla v dutinových tvarovkách se zabývalo již mnoho odborníků, ale obvyklým cílem analýz byl pouze tepelný tok ve směru kolmém na povrch stěny. Výjimky, např. práce [1-3], jsou omezeny použitými 2D modely a navíc předpokládají poměrně nízké vzduchové dutiny, které neodpovídají svými rozměry dutinám v dnes běžných izolačních cihlách. V ČR se coby průkopnická práce objevila studie [4], v níž se ovšem šíření tepla ve vzduchových dutinách modelovalo jen orientačně přes ekvivalentní tepelnou vodivost odvozenou metodikou EN ISO 6946. Nicméně i tak tato práce obrátila pozornost k fenoménu anizotropních vlastností zdiva z keramických tvarovek a inspirovala vznik detailnějších studií [5-6], které s pomocí CFD analýzy [7] určily poměry mezi ekvivalentní tepelnou vodivostí zdiva ve svislém směru a ve vodorovném směru kolmo k povrchu stěny. Cílem této studie je doplnění již publikovaných anizotropních vlastností zdiva z keramických dutinových tvarovek o ekvivalentní tepelné vodivosti zdiva ve směru rovnoběžném s povrchem zdiva.

Obr. 1 Minimální model zdiva potřebný pro výpočet ekvivalentní tepelné vodivosti (zobrazen bez polovin ložných spár)
Ekvivalentní tepelná vodivost zdiva
Ekvivalentní tepelnou vodivost zdiva lze výpočtově stanovit na základě numerického řešení šíření tepla vedením, prouděním a sáláním v charakteristickém výseku zdiva, který musí zahrnovat obvykle minimálně dvě tvarovky a k nim příslušné poloviny ložných a styčných spár (Obr. 1).
Výsledkem CFD analýzy je pak celkový tep. tok charakter. výsekem zdiva Q, který se následně použije pro výpočet výsledné ekvivalentní tepelné vodivosti:
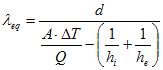
kde d je tloušťka zdiva [m], A je plocha charakteristického výseku zdiva kolmá na směr tepelného toku [m2], ΔT je rozdíl teplot [K], Q je tepelný tok [W], hi je součinitel přestupu tepla na vnitřním povrchu [W/(m2K)] a he je součinitel přestupu tepla na vnějším povrchu [W/(m2K)].
Anizotropní ekvivalentní tepelná vodivost modelového zdiva
Ve studii [5] byla publikována závislost poměru mezi ekvivalentními tepelnými vodivostmi ve svislém a vodorovném směru pro řadu modelových tvarovek, které se lišily počtem a velikostí vzduchových dutin. Celkové rozměry tvarovek zůstávaly stejné a odpovídaly běžně vyráběným tvarovkám (300 x 238 x 247 mm). Ve všech případech také tvořil vzduch 52 % z celkové plochy průřezu tvarovky (toto procento odpovídá průměrnému podílu vzduchových dutin v soudobých tvarovkách). Ložné spáry byly uvažovány v tloušťce 12 mm a styčné spáry v tloušťce 3 mm - obojí pak vyplněné lehkou maltou. Pro keramický střep byla předpokládána tepelná vodivost 0,5 W/(m.K) a pro lehkou maltu 0,2 W/(m.K).
Na Obr. 2 jsou znázorněny výsledky CFD analýzy, které dokumentují výraznou závislost poměru mezi ekv. tep. vodivostmi zdiva ve svislém a vodorovném směru na směru tepelného toku a na průměrné velikosti průřezu vzduchových dutin v keramických tvarovkách.
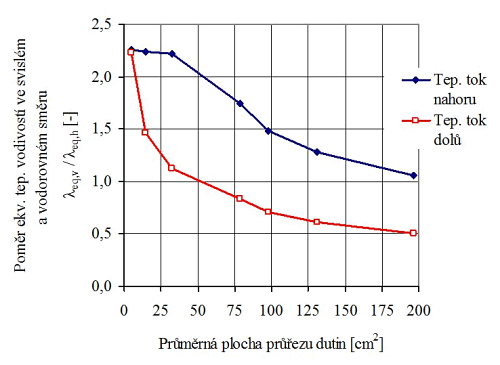
Obr. 2 Poměr mezi ekv. tep. vodivostí zdiva ve svislém a vodorovném směru a jeho závislost na průměrné průřezové ploše dutin ve tvarovce
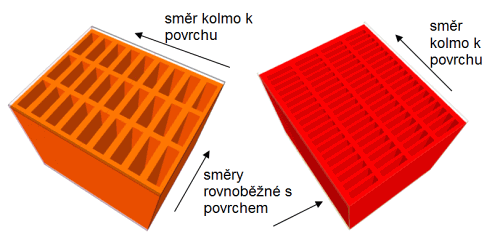
Obr. 3 Modelové dutinové tvarovky a uvažované směry tepelného toku
Stejný typ modelových tvarovek byl použit i pro odvození závislosti poměru ekvivalentních tepelných vodivostí zdiva v obou vodorovných směrech na průřezové ploše dutin ve tvarovkách. Hodnoceny byly tvarovky s průřezovou plochou dutin pod 35 cm2 (Obr. 3) coby běžnější zástupci dnešních izolačních cihel. V Tab. 1 a na Obr. 4 jsou uvedeny výsledky CFD analýzy, ze kterých je zřejmé, že tepelná vodivost modelového zdiva ve směru rovnoběžném s povrchem je zhruba 2x vyšší než ekvivalentní tepelná vodivost zdiva ve směru kolmém k povrchu.
| Počet dutin v jedné cihle |
Průměrná plocha průřezu vzduchové dutiny |
Ekvivalentní tepelná vodivost zdiva pro směr tepelného toku: | |||
| Vodorovný kolmo na povrch |
Vodorovný rovnoběžně s povrchem |
Svislý nahoru | Svislý dolů | ||
| [-] | Ac [cm2] | λeq,h1 [W/(m.K)] | λeq,h2 [W/(m.K)] | λeq,v1 [W/(m.K)] | λeq,v2 [W/(m.K)] |
| 12 | 30,0 | 0,277 | 0,499 | 0,616 | 0,309 |
| 27 | 14,5 | 0,222 | 0,422 | 0,497 | 0,324 |
| 70 | 5,0 | 0,164 | 0,344 | 0,371 | 0,365 |
Příčinou zvýšení tepelné vodivosti ve směru rovnoběžném s povrchem stěny je v daném případě jednak větší počet takto orientovaných stěn voštin (viz Obr. 3) a jednak širší vzduchové dutiny, v nichž dochází ke stále citelnému šíření tepla prouděním (Obr. 5).
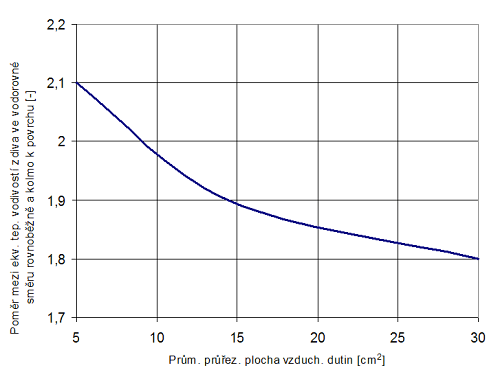
Obr. 4 Poměr mezi ekv. tep. vodivostí zdiva v obou vodorovných směrech a jeho závislost na průměrné průřezové ploše dutin ve tvarovce
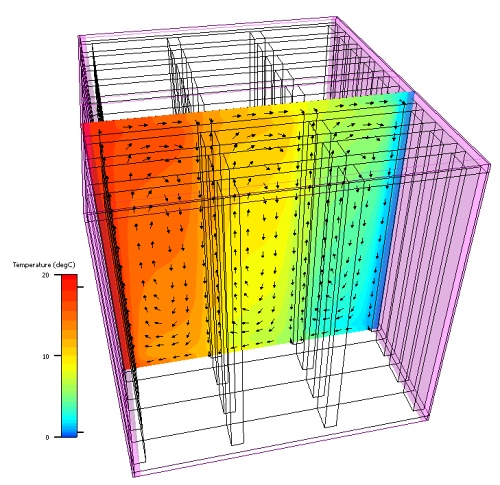
Obr. 5 Teplotní pole a orientace tepelných toků v modelové tvarovce s 27 dutinami
Anizotropní ekvivalentní tepelná vodivost skutečného zdiva
Stejně jako existují určité rozdíly mezi ekvivalentní tepelnou vodivostí modelového a skutečného zdiva pro svisle orientovaný tepelný tok [6], existují podobné rozdíly i v případě tepelného toku orientovaného vodorovně s povrchem stěny. Pokud budeme uvažovat např. tři typické, z hlediska geometrie průřezu jednodušší tvarovky z dnes dostupného sortimentu (jedna z nich - tvarovka tl. 400 mm - je zobrazena na Obr. 1), získáme dosti rozdílné výsledky (Tab. 2). Zatímco pro zdiva tl. 400 a 440 mm je ekvivalentní tepelná vodivost rovnoběžně s povrchem podle očekávání zhruba 2x vyšší než vodivost kolmo k povrchu, pro zdivo o tl. 300 mm vycházejí obě tepelné vodivosti ve vodorovném směru v zásadě shodné. Příčinou je geometrie tvarovky tl. 300 mm s poměrně velkými průřezovými plochami voštin v řezu rovnoběžném s povrchem.
Z výsledků analýzy skutečného zdiva tedy vyplývá, že pro běžné případy lze odhadnout tepelnou vodivost pro tvarovky typu Therm ve směru rovnoběžném s povrchem stěny jako dvojnásobek tepelné vodivosti uváděné výrobcem.
| Zdivo z tvarovek |
Ekvivalentní tepelná vodivost zdiva pro směr tepelného toku: | |||
| Vodorovný kolmo na povrch* |
Vodorovný rovnoběžně s povrchem |
Svislý nahoru | Svislý dolů | |
| λeq,h1 [W/(m.K)] | λeq,h2 [W/(m.K)] | λeq,v1 [W/(m.K)] | λeq,v2 [W/(m.K)] | |
| Therm 300 | 0,250 | 0,248 | 0,565 | 0,561 |
| Therm 400 | 0,131 | 0,255 | 0,353 | 0,350 |
| Therm 440 | 0,152 | 0,287 | 0,380 | 0,377 |
| * Údaj od výrobce použitý k nakalibrování CFD modelu zdiva. | ||||
Praktické důsledky anizotropie zdiva
Anizotropní vlastnosti zdiva z keramických tvarovek se projeví v řadě tepelných vazeb. Nejčastěji ovlivňuje výsledky analýzy tepelných mostů zvýšená tepelná vodivost zdiva ve svislém směru, ale existuje i řada detailů, v nichž se projeví i zvýšená tepelná vodivost ve směru rovnoběžném s povrchem stěn. Typickým zástupcem je běžný kout dvou obvodových stěn. V Tab. 3 jsou shrnuty výsledky výpočtu vnitřní povrchové teploty pro různé varianty modelu koutu, z nichž je patrné, že významnější rozdíly mezi izotropním a anizotropním modelem lze očekávat jen při nezatepleném zdivu. Případná silnější vnější tepelná izolace efekty anizotropie zcela překryje.
| Vnější zateplení | Model zdiva | Nejnižší vnitřní povrchová teplota |
Nejnižší teplotní faktor |
| θsi,min [°C] | fRsi,min [-] | ||
| ---- | Izotropní | 15,23 | 0,840 |
| Anizotropní | 14,90 | 0,831 | |
| 50 mm | Izotropní | 16,38 | 0,872 |
| Anizotropní | 16,26 | 0,868 | |
| 100 mm | Izotropní | 17,12 | 0,892 |
| Anizotropní | 17,09 | 0,891 |
Závěr
Na základě výsledků detailního CFD výpočtu modelového i skutečného zdiva lze očekávat, že tepelná vodivost zdiva z dutinových tvarovek typu Therm se bude pohybovat zhruba kolem dvojnásobku tepelné vodivosti uváděné výrobcem. Z hlediska praktických výpočtů má toto zjištění význam pouze pro nezateplené stěny - jakmile je na stěnu aplikováno vnější zateplení, význam anizotropie je prakticky zanedbatelný.
Tento příspěvek byl podpořen výzkumným záměrem VZ 04 CEZ MSM 6840770005 Udržitelná výstavba.
Literatura:
[1] Ait-Taleb T. - Abdelbaki A. - Zrikem Z.: Numerical Simulation of Coupled Heat Transfers by Conduction, Natural Convection and Radiation in Hollow Structures Heated from Below or Above, International Journal of Thermal Sciences, 47 (4): 378-387, 2008.
[2] Hasnaoui M. - Bilgen E. - Vasseur P.: Natural Convection Heat Transfer in Rectangular Cavities Partially Heated from Below, Journal of Thermophysics and Heat Transfer, 6 (2): 255-264, 1992.
[3] Calcagni B. - Marsili, F. - Paroncini, M.: Natural Convective Heat Transfer in Square Enclosures Heated from Below, Applied Thermal Engineering, 25 (16): 2522-2531, 2005.
[4] Šubrt R.: Anizotropie stavebních materiálů a její vliv na tepelné mosty, online, 2006.
[5] Svoboda, Z.: Šíření tepla ve zdivu z dutinových tvarovek ve svislém směru. Sborník konference "Simulace budov a techniky prostředí SBTP 2010", pp. 3-6, Praha 2010.
[6] Svoboda, Z. - Kubr, M.: Ekvivalentní tepelná vodivost zdiva z dutinových keramických tvarovek ve směru svislého tepelného toku. Tepelná ochrana budov 5 (2010), s. 13-17.
[7] Mentor Graphics: FloVENT 8.1, Wilsonville, Oregon 2008.
The paper focuses on the differences between equivalent thermal conductivities of the masonry from hollow bricks in vertical and in both horizontal directions. Recent CFD studies presented the ratio between thermal conductivities in vertical and in horizontal direction (perpendicular to the surface of the masonry). This study shows the relation between thermal conductivities of the masonry in both horizontal directions.