Stanovení součinitelů tlakových ztrát oblouků vzduchotechnických potrubí
Tlakové ztráty v tvarovkách jsou v návrhové fázi obtížně vypočitatelné, neboť je pro ně klíčový součinitel tlakových ztrát, jenž je proměnlivý vzhledem k typu tvarovky a její geometrii. Možností, jak získat orientační hodnotu součinitele tlakové ztráty, je experimentální měření.
Abstrakt
Tlakové ztráty ve vzduchotechnickém potrubí vznikají v místě tření proudícího vzduchu o stěny potrubí. Velikost tlakové ztráty na přímých úsecích potrubí je menší než ve vzduchotechnických tvarovkách, kde dochází zejména ke změnám směru proudnic vzduchu. Správným určením tlakových ztrát celé potrubní větve pak můžeme stanovit odpovídající výkon ventilátoru potřebný pro distribuci vzduchu do cílových prostor. Tlakové ztráty v tvarovkách jsou v návrhové fázi obtížně vypočitatelné, neboť je pro ně klíčový součinitel tlakových ztrát, jenž je proměnlivý vzhledem k typu tvarovky a její geometrii. Možností, jak získat orientační hodnotu součinitele tlakové ztráty je experimentální měření. Článek přináší rovnice součinitelů tlakových ztrát a jejich závislostí na geometrických parametrech samostatných oblouků a dvojic oblouků.
Úvod
Tlakové ztráty jsou veličinou, jenž hraje významnou roli při návrhu vzduchotechnických systémů. Výpočtem tlakových ztrát v návrhové fázi projektu lze optimalizovat výběr ventilátoru tak, aby nebyl systém zbytečně předimenzovaný [1]. Ventilační jednotka bývá prvkem v budově, který často pracuje nepřetržitě a je tedy významným konzumentem elektrické energie. Optimálním návrhem ventilátoru bez zbytečného předimenzování lze tedy docílit úsporného řešení, které může napomoci snížit energetickou spotřebu zařízení [2].
Tlakové ztráty na vzduchotechnickém potrubí dělíme na tlakové ztráty třením po délce a na místní tlakové ztráty [3]. Tlakové ztráty třením po délce vznikají v přímých úsecích potrubí a jsou relativně snadno dopočitatelné podle vztahu
(1)
[Pa]
kde λ [–] je součinitel ztráty třením, l [m] je délka přímého úseku potrubí, D [m] je hydraulický průměr potrubí, ρ [kg∙m−3] je hustota vzduchu, v [m∙s−1] je rychlost proudícího vzduchu. Z tohoto vztahu jsou známé všechny veličiny podle navrhovaného systému kromě součinitele ztráty třením λ. Tento součinitel lze empiricky dopočítat podle vztahů vycházejících z Colebrookovy-Whitovy rovnice [4] pro turbulentní proudění
(2)
[–]
kde ε [m] je absolutní drsnost potrubí, D [m] je průměr potrubí a Re [–] je Reynoldsovo číslo.
Místní tlakové ztráty lze vypočítat na základě známé rychlosti, hustoty proudícího média a součinitele tlakových ztrát.
(3)
[Pa]
kde ρ [kg∙m−3] je hustota vzduchu, v [m∙s−1] je rychlost proudění a ξ [–] je součinitel tlakových ztrát. Součinitel tlakových ztrát je obtížně stanovitelný, neboť se liší podle typu tvarovky a její geometrie. Často se stanovuje pomocí tabelárních hodnot [5], stanovených z experimentálních měření nebo numerických výpočtů [6]. Tyto součinitele lze však nalézt s rozličnými hodnotami napříč literaturami.
Tato práce se zabývá stanovením vztahů součinitelů tlakových ztrát ξ pro dané potrubní větve kruhových průřezů laboratorním měřením.
Experimentální část
Pro laboratorní experiment bylo vybráno potrubí kruhového průřezu z pozinkovaného plechu tloušťky 0,7 mm. V potrubních prvcích byly zahrnuty uklidňující kusy dlouhé 1,0 m před a za měřenou tvarovku. Dále byly použity měřené tvarovky, kterými byly oblouky, umisťované mezi uklidňující kusy.
Pro každý profil potrubí pak byly sestavovány trasy pro samostatný 90° a 45° oblouk a pro dva za sebou jdoucí oblouky opačných orientací s úhly 45° a 90° viz Obr. 2. U tratí se dvěma oblouky byly voleny délky mezilehlých částí jako poměry ku šířce zvoleného potrubí podle Tab. 1.
| DN [mm] | Průtočná plocha [m2] | Délka mezilehlého kusu [mm] | Poměr délky ku průměru potrubí |
|---|---|---|---|
| 400 | 0,126 | 800 | 1 : 2,0 |
| 400 | 1 : 1,0 | ||
| 200 | 1 : 0,5 | ||
| 200 | 0,031 | 400 | 1 : 2,0 |
| 200 | 1 : 1,0 | ||
| 100 | 1 : 0,5 | ||
| 100 | 0,008 | 200 | 1 : 2,0 |
| 100 | 1 : 1,0 | ||
| 50 | 1 : 0,5 |
Pro každý ze tří průřezů byly tedy sestaveny tratě s oblouky 1 × 90°, 4 × (2 × 45°) a 4 × (2 × 90°), jak je znázorněno na následujícím obrázku.
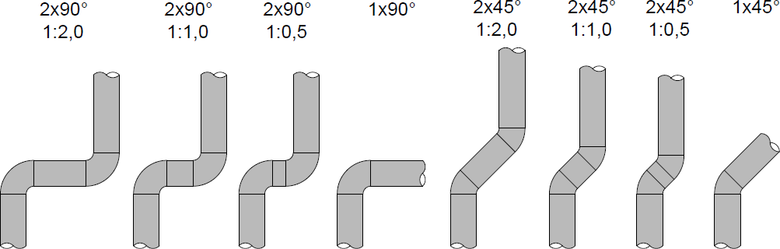
Obr. 1 Schéma všech typů sestav pro jeden průřez (popisek znázorňuje kromě typu sestavy také poměr mezi délkou mezilehlé přímé části a šířkou potrubí). Zdroj: archiv autora.
Stanovení tlakových ztrát probíhalo měřením statického tlaku před tvarovkou a za ní (vždy 3 cm před a za hranicí tvarovky), což vychází z Bernoulliho rovnice.
,
(4)
kde ρ [kg∙m−3] je hustota vzduchu, v [m∙s−1] je střední průřezová rychlost, p [Pa] je statický tlak v daném průřezu, h [m] je výškový rozdíl mezi měřenými průřezy a vztažnou rovinou a pz [Pa] jsou tlakové ztráty.
Za předpokladu konstantních středních rychlostí a nulového výškového převýšení měřicí tratě lze snadno stanovit rozdíl tlaků jako
(5)
[Pa]
Hodnoty statického tlaku byly odečítány z digitálního tlakoměru Testo 400 pro různé hodnoty průtoku vzduchu, jenž byly měřeny pomocí balometru, umístěného na konci měřicí tratě. Každá potrubní sestava byla testována pro 10 různých rychlostí proudění (10 různých objemových průtoků).
Z naměřených hodnot tlakových ztrát byly následně získány hodnoty příslušných součinitelů tlakové ztráty podle geometrie oblouku a střední rychlosti proudění kombinací vztahů (3) a (5)
(6)
[–]
kde ρ [kg∙m−3] je hustota vzduchu, v [m∙s−1] je střední průřezová rychlost, pz [Pa] je rozdíl statických tlaků před a za měřenou geometrií.
Výsledné hodnoty součinitelů tlakové ztráty byly zakomponovány do matematických vztahů.
Výsledky
Obr. 2 Schéma geometrických parametrů, použitých v rovnicích. Zdroj: archiv autora.
Rovnice závislostí součinitele tlakové ztráty na geometrii potrubí byly získány nelineární regresní metodou. Jako parametry byly v těchto rovnicích zvoleny geometrické vlastnosti měřené části potrubí; podíl zaoblení oblouku ku vnitřnímu průměru potrubí 
pro samostatné oblouky a dvojice oblouků a podíl délky mezilehlého přímého kusu ku průměru potrubí 
pro soustavu dvou oblouků. Do modelů byla zahrnuta i závislost součinitele tlakové ztráty na typu proudění, tedy na Reynoldsově čísle Re.
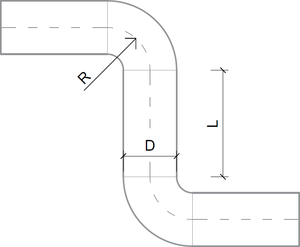
Experimentálně naměřené hodnoty jsou zpracovány do rovnic závislostí součinitele tlakových ztrát na geometrických vlastnostech soustavy a jsou zobrazeny v následující tabulce, kde ξ [–] je součinitel místních tlakových ztrát, D [m] je vnitřní poloměr potrubí, R [m] je poloměr zaoblení oblouku, L [m] je délka mezilehlého přímého kusu mezi oblouky a Re [–] je Reynoldsovo číslo.
| Typ sestavy | Vztah mezi součinitelem tlakových ztrát a tvarem tvarovky |
|---|---|
| Oblouk 1 × 90° |  |
| Oblouk 1 × 45° |  |
| Oblouky 2 × 90° |  |
| Oblouky 2 × 45° |  |
| Typ sestavy | Absolutní chyba členů rovnice | Střední kvadratická odchylka hodnot | R2 |
|---|---|---|---|
| Oblouk 1 × 90° | a = 0,100 ± 0,006 b = −4,252 ± 0,195 c = 3,462∙10−7 ± 0,914∙10−7 | RSMD = 0,0426 | R2 = 0,965 |
| Oblouk 1 × 45° | a = 0,063 ± 0,004 b = −1,182 ± 0,158 c = 1,832∙10−7 ± 0,917∙10−8 | RSMD = 0,0397 | R2 = 0,559 |
| Oblouky 2 × 90° | a = 0,096 ± 0,012 b = −4,441 ± 0,413 c = −0,072 ± 0,005 d = −4,255∙10−7 ± 9,098∙10−8 e = 0,368 ± 0,022 | RSMD = 0,0987 | R2 = 0,822 |
| Oblouky 2 × 45° | a = 0,114 ± 0,013 b = −1,564 ± 0,252 c = 0,067 ± 0,005 d = −1,400∙10−6 ± 7,254∙10−8 e = −0,253 ± 0,036 | RSMD = 0,0863 | R2 = 0,734 |
Vstupní parametry při laboratorním měření nabývaly hodnot 
, 
a Reynoldsovo číslo Re nabývalo hodnot čistě turbulentního proudění od hodnot Re > 18 000 (měření bylo provedeno pro střední rychlosti od 1,4 m∙s−1 pro potrubí o velkém vnitřním průměru, až po 29,0 m∙s−1 pro potrubí o velmi malém vnitřním průměru).
Diskuse
Při měření reálného potrubí je možné se setkat s odchylkami, kterými mohou být zejména nepřesnosti tvaru vyrobeného potrubí (například deformace nebo nýty vnikající do průtočného profilu), těsnost celé soustavy, neboť při zpracování hodnot uvažujeme s dokonale neprůvzdušnou potrubní soustavou.
Závěr
Stanovení součinitelů tlakových ztrát pro vzduchotechnické tvarovky je dlouhotrvající záležitostí, jenž zahrnuje testování rozličných potrubních tvarovek s rozličnými geometriemi. Výsledky mohou být užitečné při automatizaci návrhu potrubních větví prostřednictvím automatizované výpočtové tabulky využívající zmíněné vztahy pro výpočet součinitele tlakové ztráty, nebo pomocného výpočtového softwaru.
Experimentální data lze využít například při automatizaci výpočtů u návrhu vzduchotechnického potrubí. Zejména v BIM aplikacích, kde je možné vytvářet kompletní geometrie potrubních soustav, lze využít aproximační rovnice, které mohou vycházet z informací (geometrických) uložených v modelu budovy.
Tento článek a experimentální měření byly uskutečněny s podporou interní grantové agentury Fakulty stavební Vysokého učení technického v Brně v rámci juniorského specifického výzkumu.
Literatura
- Schild P., Mysen M. Doporučení pro měrný příkon ventilátoru (SFP) a účinnost vzduchotechnických systémů – IV. TZB-info, Praha: Jícha; 2014.
- Beránková E. Životní cyklus staveb. TZB-info, Praha: 2013.
- Chyský J., Hemzal K. Větrání a klimatizace. Třetí, zcela přepracované. Praha: B press Brno; 1993.
- Genić S., Arandjelović I., Kolendić P., Jarić M., Budimir N., Genić V. A Review of Explicit Approximations of Colebrook’s Equation. Posudek. 2011.
- Idelchik I., Grunaer D., editor, Barouch A. Handbook od Hydraulic Resistance. X/5. Moskva-Leningrad: Gosudarstvennoe Energeticheskoe Izdatel'stvo; 1960.
- Schwarzer J., Zmrhal V. Stanovení součinitelů místních ztrát s využitím CFD. Vědecký článek. 2010.
The pressure losses in the fittings are difficult to calculate in the design phase, as the key factor for them is the pressure losses, which is variable with respect to the type of fitting and its geometry. The possibility of obtaining an approximate value of the pressure loss coefficient is experimental measurements.