Stanovení součinitelů tlakových ztrát oblouků VZT potrubí – čtyřhranný průřez
Článek pojednává o měření tlakových ztrát VZT oblouků čtyřhranného průřezu. Naměřené ztráty jsou publikovány v podobě matematických závislostí geometrie měřené sestavy na hodnotě součinitele tlakové ztráty tvarovky.
Úvod
Hodnota tlakových ztrát potrubní větve je nezbytná pro návrh ventilátoru o odpovídajícím výkonu. Celková suma tlakových ztrát se skládá ze ztrát na přímých kusech potrubí a ztrátách v místech změn směru proudnic, tedy ve tvarovkách a ostatních zařízeních na potrubní větvi [1]. Výpočet tlakových ztrát často se opakujících tvarovek, u kterých se mění parametricky jejich rozměry, je obtížné z důvodu potřeby určení součinitele tlakové ztráty, který zohledňuje právě geometrii tvarovky.
Pro zjištění hodnoty součinitele lze využít numerických metod nebo experimentálního měření. Při experimentu lze naměřená data zpracovat tabelárně nebo do podoby analytických vztahů. U obojího je částečně heuristický postup hledání klíčových geometrických parametrů pro vyjádření hodnoty součinitele.
Právě experimentálním postupem při měření tlakových ztrát na vzduchotechnických obloucích čtyřhranného průřezu se zabývá tento článek, který navazuje na předchozí práci stanovení součinitelů tlakových oblouků kruhového průřezu.
Metody
Pro experiment bylo vybráno potrubí čtyřhranného průřezu s rozličnými poměry stran průřezu. Pro každý průřez pak byly vyhodnocovány tlakové ztráty samostatných oblouků 45° a 90° a dvojic oblouků za sebou jdoucích 45° a 90°, přičemž mezi touto dvojicí oblouků byly různě dlouhé přímé mezikusy.
Každá sestava začínala i končila uklidňovacím kusem, tady přímým potrubím o délce 1 m, které sloužilo k částečnému usměrnění proudu vzduchu, tak aby byl snížen vliv turbulencí na měřené hodnoty. Přehled použitých průřezů je vidět na následujícím obrázku.
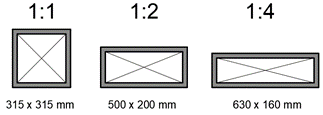
Obr. 1 Znázorněné profily potrubí použité při experimentu. Zdroj: archiv autora.
Pro sestavy dvou oblouků za sebou jdoucích byly voleny přímé mezilehlé kusy v poměru ku šířce potrubí následovně.
| Rozměry [mm] | Průtočná plocha [m2] | Délka mezilehlého kusu [mm] | Poměr délky ku průměru potrubí |
|---|---|---|---|
| 315 × 315 | 0,099 | 630 | 1 : 2,0 |
| 315 | 1 : 1,0 | ||
| 160 | 1 : 0,5 | ||
| 0 | 0 | ||
| 500 × 200 | 0,100 | 1 000 | 1 : 2,0 |
| 500 | 1 : 1,0 | ||
| 250 | 1 : 0,5 | ||
| 0 | 0 | ||
| 630 × 160 | 0,101 | 1 260 | 1 : 2,0 |
| 630 | 1 : 1,0 | ||
| 160 | 1 : 0,5 | ||
| 0 | 0 |
Tab. 1 Délky mezilehlých přímých kusů u sestav dvou oblouků za sebou jdoucích.
Stanovení součinitelů proběhlo z naměřených statických tlaků před a za tvarovkou pro danou střední průtočnou rychlost proudění podle vztahu
kde ρ [kg ∙ m-3] je hustota vzduchu, v [m ∙ s-1] je střední průtočná rychlost proudění a ξ [−] je hledaný součinitel tlakových ztrát a Δp je rozdíl statických tlaků před a za tvarovkou. Z tohoto vztahu lze snadno získat výsledný potřebný vztah pro určení hodnoty součinitele
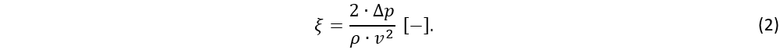
Bylo sestaveno celkem 10 tratí pro každý průřez potrubí, celkem tedy 30 tratí, které se lišily v počtu oblouků (jeden oblouk nebo dva oblouky) a v délce mezilehlého kusu u sestavy se dvěma oblouky.
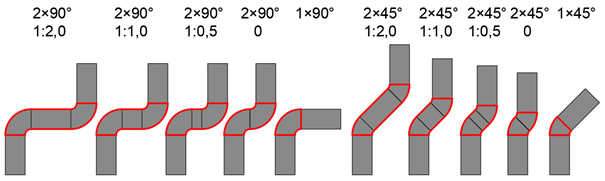
Obr. 2 Znázornění měřených tratí jednoho průřezu potrubí. U geometrií se dvěma oblouky je vypsán podíl délky mezilehlého přímého kusu ku šířce potrubí. Červeně jsou znázorněny hranice měřeného úseku.
Zdroj: archiv autora.
Hodnoty statického tlaku byly měřeny diferenčním manometrem a střední rychlost proudění byla přepočítána na základě rovnice kontinuity podle známého průtoku vzduchu, jenž byl měřen balometrem, přičemž bylo uvažováno ustálené proudění v potrubí.
Výsledky
Z naměřených hodnot byly sestaveny rovnice, zohledňující klíčové geometrické parametry oblouků. Mezi tyto parametry patří zejména hydraulický průměr DH [m], poloměr zaoblení oblouku R [m], délka mezilehlého přímého kusu L [m], šířka potrubí W [m], výška potrubí H [m] a Reynoldsovo číslo Re [−]. Veličina DH je vyjádřena vztahem
kde A [m2] je plocha průřezu potrubí a O [m] je obvod průřezu potrubí. Tento vztah platí pro čtyřhranná potrubí.
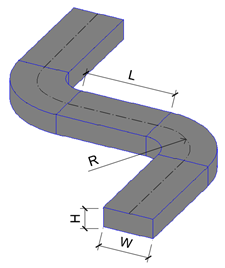
Obr. 3 Znázornění klíčových parametrů na geometrii sestavy.
Zdroj: archiv autora.
| Typ sestavy | Vztah mezi součinitelem tlakových ztrát a tvarem tvarovky |
|---|---|
| Oblouk 1 × 90° |
|
| Oblouk 1 × 45° |
|
| Oblouky 2 × 90° |
|
| Oblouky 2 × 45° |
Tab. 2 Vztahy mezi součinitelem tlakových ztrát a geometrií sestavy získané experimentálním měřením.
| Typ sestavy | Absolutní chyba členů rovnice | Střední kvadratická odchylka hodnot | R2 |
|---|---|---|---|
| Oblouk 1 × 90° | a = 0,775 ± 0,031 b = −0,224 ± 0,047 c = −0,521 ± 0,030 d = −9,508∙10−7 ± 0,980∙10−7 |
RSMD = 0,0344 | R2 = 0,932 |
| Oblouk 1 × 45° | a = 0,037 ± 0,002 b = 4,359 ± 0,100 c = −0,055 ± 0,005 d = 6,964∙10−7 ± 0,772∙10−7 |
RSMD = 0,0271 | R2 = 0,985 |
| Oblouky 2 × 90° | a = 0,732 ± 0,017 b = 2,107 ± 0,0,034 c = −0,015 ± 0,003 d = −0,056 ± 0,017 e = −9,431∙10−7 ± 2,025∙10−7 |
RSMD = 0,1460 | R2 = 0,967 |
| Oblouky 2 × 45° | a = 0,167 ± 0,006 b = 3,501 ± 0,050 c = 0,021 ± 0,002 d = 0,123 ± 0,007 e = −4,037∙10−7 ± 1,167∙10−7 |
RSMD = 0,0841 | R2 = 0,971 |
Tab. 3 Chyby měření a aproximační odchylky.
Platnost těchto vztahů je však omezena na mezní hodnoty parametrů, pro které byla tato úloha měřena. Vstupní měřené parametry byly
![]()
![]()
![]()
![]()
![]()
Reynoldovo číslo bylo vždy Re > 28 000. Mimo horní a spodní limitní hodnoty parametrů nenabývají rovnice platnosti.
Pro zvolené oblouky v intervalu platnosti rovnic byly porovnány hodnoty součinitele tlakové ztráty s dalšími zdroji. Jsou uvažovány oblouky s vnitřním poloměrem zaoblení 150 mm. Byla také stanovena jednotná hodnota Reynoldsova čísla na 50 000. Tyto hodnoty jsou uvažovány z důvodu počtu a typu parametrů zohledněných v rovnicích. Nejsou často v souladu s parametry, uváděnými v ostatních zdrojích.
| Rozměry potrubí W × H | Hodnoty podle ASHRAE [2] | Hodnoty podle Idelchick [3] | Hodnoty z rovnic |
|---|---|---|---|
| 315 × 315 mm | 0,21 | 0,24 | 0,21 |
| 630 × 160 mm | 0,61 | 0,35 | 0,50 |
| 400 × 200 mm | 0,36 | 0,31 | 0,42 |
| 500 × 200 mm | 0,48 | 0,50 | 0,46 |
| 450 × 140 mm | 0,44 | 0,34 | 0,47 |
Tab. 4 Porovnání hodnot pro oblouk 1 × 90°.
| Rozměry potrubí W × H | odnoty podle ASHRAE [2] | Hodnoty podle Idelchick [3] | Hodnoty z rovnic |
|---|---|---|---|
| 315 × 315 mm | 0,13 | 0,16 | 0,01 |
| 630 × 160 mm | 0,37 | 0,39 | 0,53 |
| 400 × 200 mm | 0,22 | 0,20 | 0,13 |
| 500 × 200 mm | 0,29 | 0,31 | 0,17 |
| 450 × 140 mm | 0,26 | 0,22 | 0,45 |
Tab. 5 Porovnání hodnot pro oblouk 1 × 45°.
| Rozměry potrubí | L / W | |||
|---|---|---|---|---|
| 2 : 1 | 1 : 1 | 0,5 : 1 | 0 | |
| 315 × 315 mm | 0,56 (0,45) |
0,58 (0,45) |
0,58 (0,56) |
0,59 (0,66) |
| 630 × 160 mm | 2,46 (0,63) |
2,49 (0,63) |
2,51 (0,63) |
2,53 (0,92) |
| 400 × 200 mm | 1,18 (0,59) |
1,20 (0,59) |
1,21 (0,65) |
1,22 (0,86) |
| 500 × 200 mm | 1,37 (0,95) |
1,39 (0,95) |
1,40 (1,00) |
1,42 (1,40) |
| 450 × 140 mm | 2,29 (0,96) |
2,31 (0,96) |
2,32 (1,05) |
2,33 (1,41) |
Tab. 6 Porovnání hodnot z rovnic pro sestavu 2 × 90°. Hodnoty od Idelchick [3] jsou uvedeny v závorce.
Tabelární hodnoty pro sestavu 2 × 45° jsou obtížně porovnatelné s dalšími zdroji, neboť tento údaj v literatuře často chybí. Pro alespoň rámcové porovnání je zde tabulka hodnot od Idelchick [3], kdy jsou hodnoty přenásobeny součinitelem podle úhlu oblouku. Hodnoty tohoto součinitele jsou původně použity při výpočtu součinitele tlakové ztráty samostatného oblouku. Pro sestavu dvou oblouků pak není v této literatuře zohledněn.
| Rozměry potrubí | L / W | |||
|---|---|---|---|---|
| 2 : 1 | 1 : 1 | 0,5 : 1 | 0 | |
| 315 × 315 mm | 0,30 (0,28) |
0,28 (0,28) |
0,27 (0,35) |
0,26 (0,41) |
| 630 × 160 mm | 1,48 (0,40) |
1,42 (0,40) |
1,40 (0,40) |
1,38 (0,58) |
| 400 × 200 mm | 0,54 (0,37) |
0,51 (0,37) |
0,49 (0,41) |
0,47 (0,53) |
| 500 × 200 mm | 0,64 (0,59) |
0,61 (0,59) |
0,59 (0,62) |
0,57 (0,86) |
| 450 × 140 mm | 1,28 (0,60) |
1,25 (0,60) |
1,23 (0,66) |
1,22 (0,87) |
Tab. 7 Porovnání hodnot z rovnic pro sestavu 2 × 45°. Hodnoty od Idelchick [3] jsou uvedeny v závorce, přičemž jsou přenásobeny součinitelem pro úhel oblouku rovnající se 45°, který původně není pro tuto sestavu ve zdroji zahrnut.
Diskuse
Publikované rovnice mají omezený platný rozsah a při extrapolaci nemůže být zaručena hodnota výsledků. Srovnání takto obdržených vztahů je obtížné z důvodu množství parametrů, obsažených v rovnicích a také nekonzistentnosti mezi parametry zvolenými v této práci a parametry u jiných autorů. Lze tedy pouze porovnávat typy sestav s takovými parametry, které jsou v rozmezí platnosti rovnic, a které lze porovnat s jinými autory.
Závěr
Výsledky práce navazují na předchozí uskutečněný výzkum týkající se hodnot tlakových ztrát oblouků kruhového průřezu. Výsledky měření jsou zpracovány do analytických rovnic popisující vztah mezi hodnotou součinitele a geometrií dané tvarovky.
Rovnice lze využít zejména pro rozvoj automatizace výpočtu tlakových ztrát ať už prostřednictvím BIM nebo jiných metod.
Tento článek a experimentální měření byly uskutečněny s podporou interní grantové agentury Fakulty stavební Vysokého učení technického v Brně v rámci juniorského specifického výzkumu 2019.
Literatura
- Janalík J, Šťáva P. Mechanika tekutin. n.d.
- Howell R, Sauer H, Coad W. Principles of Heating, Ventilating, and Air Conditioning. ilustrované vydání. Atlanta: American Society of Heating, Refrigerating and Air-Conditioning Engineers; 2005.
- Idelchik I, Grunaer D, editor, Barouch A. Handbook od Hydraulic Resistance. X/5. Moskva-Leningrad: Gosudarstvennoe Energeticheskoe Izdatel'stvo; 1960.
