Filtrace atmosférického vzduchu I

Základní operací při ochraně a tvorbě vnitřního ovzduší před tuhými a kapalnými znečišťujícími látkami (částicemi) je filtrace atmosférického vzduchu.

Ve větrání a klimatizaci je filtrace atmosférického vzduchu základní způsob k dodržení požadované čistoty vnitřního ovzduší ve větraném a klimatizovaném prostoru, dále slouží při ochraně větracích a klimatizačních zařízení (zejména výměníky tepla).

Vícestupňová filtrace je nepostradatelnou součástí vysoce účinné filtrace při vytváření čistých prostorů, kde požadavky na vysokou čistotu vzduchu vyplývají z požadavků jednotlivých technologických procesů i ochrany pracovníků.

Filtry atmosférického vzduchu jsou nedílnou součástí odsávacích a odlučovacích systémů ve vnitřním pracovním prostředí, kde je možno v souladu s hygienickými požadavky na pracovní prostředí [Nařízení vlády č. 361/2007 Sb., kterým se stanoví podmínky ochrany zdraví při práci] po vyčištění oběhového vzduchu pod 5 % příslušného expozičního limitu a splnění dalších požadavků vracet vzduch zpět na pracoviště nebo odsávací systém je součástí vzduchotechnického systému s využitím zpětného získávání tepla v odváděném vzduchu. Typickým příkladem jsou odsávací zařízení ve svařovnách a průmyslu zpracování dřeva.

Součástí filtračních systémů ve vnitřním prostředí je i využití sorpčních filtrů k zachycování plynných znečišťujících látek a pachů (odérů). K zachycování jemných částic se zde rovněž využívá elektrických odlučovacích principů - elektrofiltry a dielektrické filtry.

1 Teorie filtrace částic

1.1 Frakční odlučivost izolovaného vlákna a vláknité vrstvy

Základem filtrace částic atmosférického vzduchu je odlučování částic ve vláknité vrstvě, složené z filtračních vláken. Při filtraci dochází k odlučování částic na jednotlivých vláknech a poté i na již odloučených částicích. Protože se částice odlučují uvnitř vláknité vrstvy, jedná s o tzv. hloubkovou filtraci.

Každá vláknitá vrstva se charakterizuje několika základními veličinami:

• tloušťka vrstvy s, která v závislosti na druhu a účelu použití filtračního materiálu dosahuje hodnot od desetin mm až po jednotky cm,
• poréznost ε (1) nebo objemové zaplnění c (1), které jsou definovány jako poměr objemu vláken, resp. mezer, k objemu vrstvy. Musí proto platit ε + c = 1 . Poréznost ε dosahuje v závislosti na druhu a účelu použití filtračního materiálu hodnot ε > 0,8 (u vysoeúčinných filtračních materiálů ε > 0,9),
• střední aritmetický průměr vláken d_N,1, který opět závisí na druhu a účelu použití filtračního materiálu a např.u vysoceúčinných filtrů dosahuje hodnot řádově desetiny až jednotky μm.

Výsledným parametrem, který předurčuje vlastnosti filtračního materiálu, je parametr vrstvy λ (1), který je s použitím výše uvedených veličin definován jako

Čím vyšší je hodnota λ, tím vyšších odlučivostí lze ve vrstvě dosáhnout. Dosažení vysoké hodnoty λ cestou snižování hodnoty poréznosti ε a zvyšování tloušťky vrstvy s je omezeno tlakovou ztrátou filtrační vrstvy, která kromě jiných veličin rovněž závisí na těchto dvou veličinách.

Výsledná závislost frakční odlučivosti vláknité vrstvy na velikosti částice O_f (a), která je rozhodující a nejdůležitější vlastností filtračního materiálu, vychází z frakční odlučivosti částic na izolovaném vlákně O_f,i (a) a mezi oběma závislostmi pro jednotlivé velikosti částic platí

Vzájemnou souvislost mezi O_f(a), O_f,i(a) a λ dle vztahu (2) lze vyjádřit graficky - obr. 1.

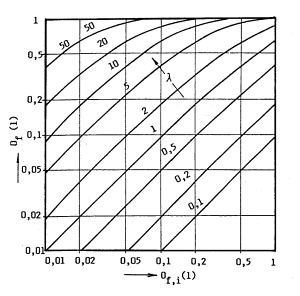
Obr. 1 Vzájemná souvislost mezi O_f(a), O_f,i(a) a λ

Z tohoto vyjádření je zřejmé, že u vláknité vrstvy s parametrem λ ≥ 1 - 2 je výsledná frakční odlučivost vrstvy O_f(a) větší než frakční odlučivost izolovaného vlákna O_f,i(a).

Vzájemný vztah (2) je čistě teoretický, odvozený za určitých zjednodušujících předpokladů - vlákna jsou ve vrstvě rovnoměrně rozdělena a všechna jsou orientována kolmo na směr proudu vzduchu. Dále se předpokládá, že částice, které se některým z odlučovacích principů dostanou na povrch vlákna, na něm ulpí a považujeme je za odloučené.

Skutečné podmínky při odlučování částic v reálné vláknité vrstvě se ve vztahu (2) respektují zavedením korekčních součinitelů γ₁(1) na nedokonalé rozdělení vláken ve vrstvě a γ₂(1) na strhávání a odskok již odloučených částic, kterými se koriguje frakční odlučivost izolovaného vlákna O_f,i(a). Zavedením těchto součinitelů se vztah (2) změní na

Korekce γ₁ je dána kvalitou provedení vláknité vrstvy a její hodnota nezávisí na velikosti částice. U reálných vláknitých vrstev dosahuje hodnot γ₁ ≅ 0,4 - 0,7 . U korekce γ₂ významnou roli sehrávají materiálové vlastnosti částice a vlákna (tvrdost a pružnost) a kromě závislosti na těchto vlastnostech platí, že hodnota součinitele γ₂ se snižuje (korekce se zvyšuje) se zvětšující se velikostí částice a, zvyšující se rychlostí vzduchu ve vrstvě a zmenšujícím se průměrem vlákna. Korekce γ₂ je tak sice funkcí velikosti částice, ale ovlivňuje spíše chování větších částic než submikronových velikostí (a < 1 μm), na které je při filtraci soustředěna největší pozornost. Z těchto důvodů je proto možno konstatovat, že součinitele γ₁ a γ₂ sice ovlivňují přepočet mezi frakční odlučivostí částic na izolovaném vlákně O_f,i(a) a ve vrstvě O_f,(a), ale zásadním způsobem neovlivňují charakter těchto závislostí typický tím, že zde existuje určitá oblast velikostí částic, které se nejhůře odlučují.

Klíčem k pochopení charakteru výsledné závislosti O_f,(a) je proto charakter závislosti frakční odlučivosti na izolovaném vlákně O_f,i(a).

Označíme-li filtrační rychlost (čelní rychlost vzduchu před vláknitou vrstvou) jako v₁, je rychlost vzduchu ve vláknité vrstvě v_ε větší a platí pro ni vztah

V teorii filtrace se rychlost v_ε považuje za rychlost nabíhajícího proudu vzduchu na vlákno.

Při obtékání vlákna průměru d (m), resp. d_N,1, rychlostí v_ε (m/s) se na odlučování částic současně podílejí tři hlavní odlučovací principy: difúzní, intercepční a setrvačný.

Difúzní odlučovací princip je způsoben náhodným pohybem částic vlivem nárazů molekul plynu na částice. Rozhodující Pecletovo kritérium P_e je zde definováno vztahem

Pro vazké obtékání vlákna a s uvažováním vlivu sousedních vláken na charakter proudového pole lze pro frakční odlučivost difúzí na izolovaném vlákně O_dif,i psát kriteriální vztah

Vzhledem k laminárnímu charakteru proudění ve vláknité vrstvě se ve vztahu (5) u difúze částic uplatňuje součinitel tepelné (Brownovské) difúze D_B. Pro D_B (m²/s) obecně platí vztah

kde k je Boltzmannova konstanta, k = 1,3805 . 10^-23 J/K, T(K) je absolutní teplota plynu a B (s/kg) je tzv. pohyblivost částice. Pro B platí vztah

kde v čitateli je již dříve zmíněná Cunninghamova korekce aerodynamického odporu na skluz plynu na povrchu částice, která nabývá významu u menších částic, jejichž velikost a je srovnatelná se střední volnou dráhou molekul plynu l_m (u vzduchu l_m ≅ 0,065 μm). K_c je Cunninghamova konstanta, K_c ≅ 2,7.

Ze vztahů (7) a (8) jasně vyplývá, že čím je velikost částice a menší, tím je pohyblivost B i součinitel difúze D_B větší, zejména však u částic a < 1 μm, kde se začíná výrazným způsobem projevovat korekce odporu na skluz plynu.

Ze vztahů (5) a (6) pak plyne, že účinnost difúzního odlučování na izolovaném vlákně O_dif,i se snižuje se zvyšující se hodnotou Pecletova kritéria, tj. zvětšující se velikostí částice.

Intercepční odlučovací princip nabývá ve filtraci atmosférického vzduchu velkého významu, neboť parametr intercepce α, definovaný vztahem

může u vláknitých vrstev vyrobených z jemných vláken (zejména filtrační materiály vyráběné papírenskou technologií) dosáhnout u větších částic i hodnot α > > 1. Pro vazké obtékání vlákna a s uvažováním vlivu sousedních vláken na charakter proudového pole lze pro frakční odlučivost vlivem intercepce na izolovaném vlákně O_int,i psát

Se zvyšující se hodnotou parametru intercepce α a tedy velikostí částice a se hodnota účinnosti O_int,i zvyšuje téměř kvadraticky.

Setrvačný odlučovací princip se uplatňuje zejména při odlučování větších částic a rozhodující Stokesovo kritérium S_tk je definováno vztahem (za charakteristický rozměr se zde používá střední aritmetický poloměr vláken d_N,1/2)

Pro vazké obtékání vlákna, dané hodnotou Reynoldsova čísla obtékání vlákna Re_d, lze pro frakční odlučivost vlivem setrvačnosti na izolovaném vlákně O_setrv,i psát

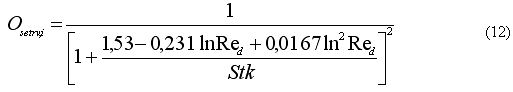
Reynoldsovo číslo Re_d je zde definováno jako

Ze vztahů (11) a (12) vyplývá, že se zvětšující se velikostí částice se zvyšuje hodnota S_tk i frakční odlučivost O_setrv,i. Závislost O_setrv,i(a) dle (12) má typický charakter "S" - křivky.

S malou nepřesností je možno při odlučování částic na izolovaném vlákně uvažovat aditivní princip a pro výslednou frakční odlučivost částice na izolovaném vlákně O_f,i jednoduše psát

Ze vztahu (14) a odpovídajících výše uvedených vztahů plyne, že výsledná frakční odlučivost izolovaného vlákna O_f,i je funkcí více veličin

Chceme-li proto ze vztahu (14) odvodit požadovanou závislost O_f,i(a), je nutno současně uvést, pro jaké konkrétní hodnoty ostatních veličin (např. d_N,1, v_ε) tato závislost platí.

Na obr. 2 je ukázka výsledné závislosti O_f,i(a) a dílčích závislostí jednotlivých odlučovacích principů z oblasti vysoceúčinné filtrace, kde pro výpočet byly použity následující hodnoty základních parametrů: střední aritmetický průměr vláken d_N,1 = 1 μm, filtrační rychlost v₁ = 0,03 m/s, poréznost ε = 0,92 (v_ε = 0,0326 m/s) a běžné parametry vzduchu. Hustota částic se ve výpočtu uvažuje ρ_č = 2000 kg/m³.

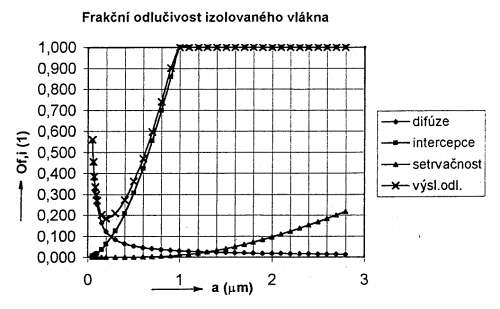
Obr. 2 Závislost O_f,i(a) pro podmínky u vysoceúčinné filtrace

Na dalším obr. 3 je obdobně zobrazen průběh O_f,i(a) a dílčích závislostí jednotlivých odlučovacích principů pro podmínky izolovaného vlákna při filtraci u běžného větrání: d_N,1 = 10 μm, filtrační rychlost v₁ = 0,1 m/s, poréznost ε = 0,92 (v_ε = 0,109 m/s).

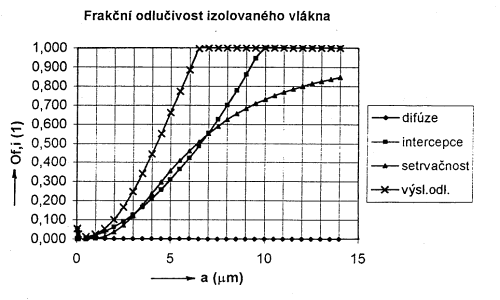
Obr. 3 Závislost O_f,i(a) pro podmínky u filtrace u běžného větrání

Z porovnání obou zvolených případů zcela jasně vyplývá, že za podmínek vysoceúčinné filtrace (jemná vlákna a nízká filtrační rychlost) se na výsledném charakteru závislosti O_f,i(a) v oblasti velikostí částic do 1 μm významným způsobem podílí difúzní a intercepční odlučovací princip a naopak setrvačný princip je v této oblasti téměř zanedbatelný. Protože s rostoucí velikostí částice se O_dif,i snižuje a naopak O_int,i zvyšuje, je výsledná závislost O_f,i(a) charakteristická tím, že zde existuje určitá velikost částice, která se na vlákně nejhůře odlučuje.

Za podmínek obtékání vlákna ve filtraci u běžného větrání (hrubší vlákna a vyšší filtrační rychlost) se na výsledném odlučovacím efektu u větších částic podílí setrvačný a intercepční odlučovací princip. V oblasti velikostí částic do 1 μm jsou hodnoty výsledné frakční odlučivosti izolovaného vlákna O_f,i(a) velmi nízké, neboť se za daných podmínek i difúzní odlučovací princip stává zanedbatelným.

Jak již bylo uvedeno, charakter závislosti O_f,i(a) se odpovídajícím způsobem projeví prostřednictvím vztahů (2) a (3) i na výsledné závislosti frakční odlučivosti vláknité vrstvy O_f (a) a tím i celého filtru. Závislost O_f (a) je vlastností filtru a rozhoduje o jeho výsledných odlučovacích schopnostech. O této problematice je blíže pojednáno v části 2.

1.2 Účinnost filtrace

Uživatele filtrů atmosférického vzduchu nejvíce zajímá výsledný účinek odlučovacích schopností filtru na odlučování nečistot a příměsí ve vzduchu - účinnost filtrace. Ta záleží nejenom na závislosti frakční odlučivosti vláknité vrstvy O_f (a), ale i charakteru znečištění atmosférického vzduchu pevnými a kapalnými částicemi, vyjádřeném zejména jejich početní nebo hmotnostní distribucí (křivky relativních četností, propadů nebo zbytků).

Účinnost filtrace se v praxi podobně jako u filtrace průmyslové vyjadřuje celkovou odlučivostí O_c (%), kterou lze s použitím koncentrací příměsí před filtrem C_p a koncentrací na výstupu z filtru C_v definovat jako

Opakem celkové odlučivosti O_c je celkovým průnik P_c (%), definovaný vztahem

Koncentrace příměsí se uvádějí buď jako hmotnostní, např. v (mg/m³) nebo (μg/m³), nebo početní (1/m³). Použití rozdílných koncentrací dává u shodného filtru až řádově rozdílné výsledky ve vyjádření O_c, resp. P_c.

1.3 Tlaková ztráta čisté vláknité vrstvy

Kromě odlučovacích schopností čisté vláknité vrstvy, vyjádřené závislostí frakční odlučivosti O_f (a), je nejdůležitější charakteristikou vláknité vrstvy její počáteční tlaková ztráta (tlaková ztráta čisté vláknité vrstvy) a její změna se zanášením.

Tlakovou ztrátu čisté vláknité vrstvy Δp_z,0 (Pa) lze teoreticky odvodit z odporové síly působící na vlákna ve vrstvě při jejich obtékání vzduchem a z čelní plochy vláknité vrstvy. Tímto postupem dospějeme ke vztahu

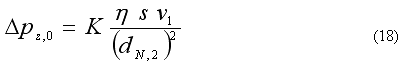
kde d_N,2 je střední kvadratický průměr vláken a K konstanta úměrnosti, která obecně zahrnuje vliv Reynoldsova čísla obtékání vláken Re_d (13) na součinitel odporu vlákna, vzájemné působení sousedních vláken na charakter proudového pole při obtékání vlákna a i změnu odporu při obtékání jemných vláken vlivem skluzu plynu na povrchu vlákna.

V oboru filtrace atmosférického vzduchu se při vyjádření tlakové ztráty pracuje spíše s poloměry vláken r = d/2, takže místo vztahu (18) lze pro tlakovou ztrátu Δp_z,0 (Pa) psát

a parametr Π se nazývá bezrozměrná tlaková ztráta. Pro vyjádření Π existuje v literatuře celá řada teoreticky odvozených i experimentálně stanovených vztahů, z nichž jednoduchý a všeobecně uznávaný vztah je

který předpokládá laminární charakter obtékání vláken (Re_d ≤ 1) a veličinou c (objemové zaplnění) se respektuje vliv sousedních vláken na charakter proudového pole.

Z obou vztahů (18) i (19) je zřejmé, jaký vliv na tlakovou ztrátu mají jednotlivé veličiny. Nutno zdůraznit lineární změnu Δp_z,0 s čelní rychlostí v₁ a značný vliv průměru vláken, vyjádřený druhou mocninou střední kvadratické velikosti d_N,2, resp. r_N,2.

1.4 Tlaková ztráta filtru

Tlaková ztráta filtru v čistém stavu Δp_f,0 (Pa) se poněkud liší od tlakové ztráty filtračního materiálu (vláknité vrstvy) Δp_z,0 (Pa), neboť v závislosti na provedení filtru je nutno kromě tlakové ztráty vlastního filtračního materiálu uvažovat i ztráty na vstupu a výstupu vlivem změny směru vzduchu a u skládaných filtrů i ztráty třením při průchodu vzduchu jednotlivými štěrbinami vytvořenými filtračním materiálem nebo separátory vloženými mezi jednotlivé sklady. Zároveň je nutno si uvědomit, že u reálných filtrů neprotéká vzduch filtračním materiálem ideálně kolmo na jeho povrch, ale v závislosti na typu filtru pod určitým úhlem ≤ 90°. Vše má za následek, že změna tlakové ztráty filtru se změnou objemového průtoku není čistě lineární jako u vlastního filtračního materiálu dle vztahů (18) i (19).

Pro provoz filtrů atmosférického vzduchu je důležitá znalost změny jejich tlakové ztráty Δp_f se zanášením. Tuto závislost lze, podobně jako u změny tlakové ztráty filtračního materiálu Δp_z se zanášením, graficky vyjádřit např. závislostí na obr. 4, kde na vodorovné

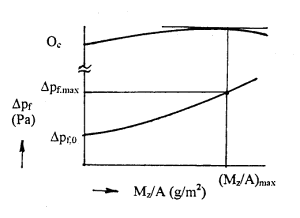
Obr. 4 Závislost změny tlakové ztráty filtru se zanášením

ose je vynesena poměrná hmotnost zachycených částic M_z (g) a velikosti filtrační plochy A (m²) a na svislé ose změna tlakové ztráty filtru Δp_f od její počáteční hodnoty Δp_f,0 (Pa). Tuto závislost je nutno zjistit experimentálně pro daný filtr a konkrétní podmínky jeho použití, tj. filtrační rychlost i charakter odlučovaných příměsí. Nutno upozornit na skutečnost, že se změnou velikosti odlučovaných příměsí se podstatným způsobem mění charakter závislosti Δp_f (M_z/A) a nelze proto přejímat závislosti zjištěné v laboratoři s různými zkušebními prachy a považovat je za závislost změny tlakové ztráty filtru při odlučování atmosférického prachu. Obecně zde platí, že čím jemnější jsou částice odlučovaného prachu, tím je při stejné hodnotě M_z/A (g/m²) změna Δp_f větší.

Se zanášením filtru dochází nejenom k výrazné změně tlakové ztráty, ale může docházet i ke změně jeho odlučovacích vlastností. Při zanášení vláknité vrstvy odloučenými částicemi se postupně snižuje poréznost vrstvy ε a tím zvyšuje rychlost vzduchu ve vrstvě v_ε a následně i dynamický účinek proudu na již odloučené částice. Po počátečním nárůstu celkové odlučivosti O_c se zanášením, které lze vysvětlit zvyšováním hodnoty parametru vrstvy λ, dochází při dalším zanášení zejména u filtrů pro běžné větrání k jejímu postupnému snižování vlivem strhávání odloučených částic, které tak postupně "prorůstají" vláknitou vrstvou. Z těchto důvodů se u filtrů atmosférického vzduchu omezuje nárůst tlakové ztráty na určitou hodnotu Δp_f,max, např. dvojnásobek počáteční tlakové ztráty Δp_f,0 nebo ze zkušeností stanovenou určitou konkrétní hodnotu. Hmotnost zachyceného prachu (M_z/A)_max , která odpovídá dané hodnotě Δp_f,max (obr. 4), se nazývá jímavost filtru a při známé vstupní koncentraci příměsí lze z této hodnoty odhadnout životnost filtru, tj. dobu jeho provozu do následné výměny.

Použitá literatura

Hemerka J.: Odlučování tuhých částic, Vydavatelství ČVUT, 2000
Nový R. a kol.: Technika prostředí, Vydavatelství ČVUT, 2006 (kapitola 6)
Székyová M., Ferstl K., Nový R.: Větrání a klimatizace, Vydavatelství JAGA, Bratislava,2006 (kapitola 10.4)
Firemní literatura