Reklama

Vliv tepelné ztráty potrubí na energetickou bilanci solární soustavy

doc. Ing. Petr Horák, Ph.D., Ing. Karolína Vyhlídalová

Recenzovaný

Článek se zabývá analýzou tepelné ztráty trubních rozvodů v modelu malé solární soustavy vytvořené v energetickém simulačním nástroji TRNSYS. Pozornost je věnována dopadu ztráty tepla potrubím na celkovou energetickou bilanci. Bylo zvoleno několik variant délky potrubí pro jeden typ soustavy. Výsledky uvedené v články názorně prezentují vliv různých délek potrubí na tepelné ztráty a následný dopad na energetickou bilanci sledované soustavy.

Reklama

1. Úvod

Technická praxe si často klade otázku, jaký vliv má tepelná ztráta potrubí na celkovou energetickou bilanci tepelné soustavy. Zda je nutné tento vliv respektovat, nebo je možné jej zanedbat. Cílem zkoumání tohoto článku je posouzení různých délek, jejich tepelných ztrát a celkový dopad délky potrubí na energetickou bilanci solární soustavy. Při návrhu solární soustavy je možné vycházet z TNI 73 0302 [1]. Tato norma však není postačující na přesné výpočty tepelných ztrát potrubím. Proto jsme použili pro přesnější bilanci tepelných ztrát potrubí energetický simulační nástroj TRNSYS [2]. Pro dosažení cíle článku bylo záměrně využito modelování, protože zjistit poklesy teplot na jedné reálné solární soustavě při různých délkách potrubí by bylo velice náročné. Při měření na reálné solární soustavě by se musela v okruhu postupně měnit délka potrubí. S každou délkou potrubí (celkem deset délek) by se pak provádělo roční měření. To znamená, že celkem by se muselo 10 let měřit, než by se získala potřebná data. Modelování s nástrojem TRNSYS nám celý proces zjednoduší. Nástroj umožňuje vytvořit výpočtový model, na který se potom aplikují reálná klimatická data a provede se roční simulace pro různé délky potrubí.

Obr. 1 Schéma výpočtového modelu solární teplovodní soustavy

2. Výpočtový model

2.1 Základní popis modelu solární soustavy

Na základě reálné solární tepelné soustavy instalované v areálu Fakulty stavební, Vysokého učení technického v Brně, byl vytvořen a odladěn výpočtový model v energetickém simulačním nástroji TRNSYS. Soustava obsahuje akumulační zásobník o objemu 200 l, dva ploché kapalinové kolektory o celkové ploše 4 m². Parametry kolektoru jsou: účinnost kolektoru η₀ = 0,788 [–], lineární součinitel tepelné ztráty a₁ = 4,207 W‧m⁻²‧K⁻¹, kvadratický součinitel tepelné ztráty a₂ = 0,024 W‧m⁻²‧K⁻². Kolektory jsou instalovány na nezastíněné střeše budovy ve sklonu 45° s azimutovým úhlem 0° (jih). Solární soustava dále obsahuje nezbytné armatury a vybavení, čerpadlovou skupinu. Ve výpočtu je uvažováno s odběrem TV pro 4 osoby, každá se spotřebou 50 l‧den⁻¹. Použitá klimatická data jsou desetiletým průměrem z meteorologické stanice Kuchařovice (okres Znojmo). v interiéru se po celou dobu simulace uvažovalo s teplotou 20 °C.

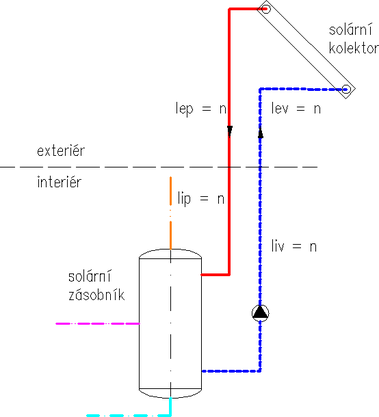
Schéma modelu vytvořeného pro účely simulace solární teplovodní soustavy s nepřímým ohřevem teplé vody je zobrazen na obrázku 1.

Pro simulace byla využita sestava s dvojicí plochých kapalinových kolektorů, viz popis výše. Na obrázku 1 je úsek l_iv vratné potrubí v interiéru, l_ev pak vratné potrubí v exteriéru. Analogicky je l_ip přívodní potrubí v interiéru a l_ep přívodní úsek potrubí v exteriéru. Každý zmíněný úsek má délku n, přičemž simulace byla provedena pro délky n = 0, 1, 2, 3, ..., 10 m.

2.2 Parametry potrubí a tepelné izolace v modelu

Bylo zvoleno měděné potrubí 28 × 1,5 mm. Vnější průměr trubky je d_p = 28 mm s tloušťkou stěny s_p = 1,5 mm a povrch trubky délky 1 m je S₁ = 0,0880 m²‧m⁻¹ [3]. Tepelná vodivost potrubí je λ_p = 393 W‧m⁻¹‧K⁻¹ [4]. Potrubí je opatřeno tepelnou izolací tloušťky 50 mm s hodnotou tepelné vodivosti λ_iz = 0,04 W‧m⁻¹‧K⁻¹, součinitel sálání povrchu tepelné izolace C = 4,65 W‧m⁻²‧K⁻⁴. Ve výpočtu je uvažováno s použitím teplonosné látky na bázi polypropylenglykolu v objemové koncentraci 60 %. Parametry pro teplonosnou kapalinu jsou pro uvažovanou průměrnou teplotu 50 °C: hustota ρ = 1013 kg‧m⁻³, kinematická viskozita ν = 1,38.10⁻⁶ m²‧s⁻¹, tepelná kapacita c = 3,95 kJ‧kg⁻¹‧K⁻¹, tepelná vodivost λ = 0,38 W‧m⁻¹‧K⁻¹ a rychlost proudící kapaliny w = 0,27 m‧s⁻¹.

2.3 Stanovení měrného tepelného toku

Součinitel prostupu tepla trubních rozvodů se určuje podle vyhlášky č. 193/2007 Sb. [5]. Tato vyhláška stanovuje vztah pro výpočet součinitele prostupu tepla potrubí s uvažováním tepelné izolace včetně hodnot součinitelů prostupu tepla pro potrubí jednotlivých dimenzí, viz vztah 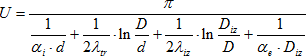(1).

(1)

kde je

U: součinitel prostupu tepla [W‧m⁻²‧K⁻¹],
d: vnitřní průměr trubky [m],
D_iz: vnější průměr izolace [m],
D: vnější průměr potrubí [m],
α_e: součinitel přestupu tepla na povrchu izolace [W‧m⁻²‧K⁻¹],
α_i: součinitel přestupu tepla na vnitřní straně trubky [W‧m⁻²‧K⁻¹],
λ_iz: součinitel tepelné vodivosti tepelné izolace [W‧m⁻¹‧K⁻¹],
λ_tr: součinitel tepelné vodivosti materiálu trubky [W‧m⁻¹‧K⁻¹].

Dále je třeba stanovit součinitel přestupu tepla α_i. Výpočet je uveden ve vztahu (2) a vychází z odborné literatury [6].

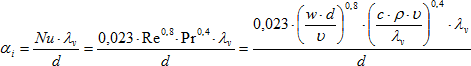(2)

kde je

α_i: součinitel přestupu tepla na vnitřní straně trubky [W‧m⁻²‧K⁻¹],
Nu: Nusseltovo číslo,
Re: Reynoldsovo číslo,
Pr: Prandtlovo číslo,
w: rychlost proudění kapaliny v trubce [m‧s⁻¹],
λ_v: tepelná vodivost kapaliny v závislosti na teplotě [W‧m⁻¹‧K⁻¹],
d: vnitřní průměr trubky [m],
c: měrné tepelná kapacita kapaliny v závislosti na teplotě [J‧kg⁻¹‧K⁻¹],
ρ: měrná hmotnost kapaliny v závislosti na teplotě [kg‧m⁻³],
v: kinematická viskozita kapaliny v závislosti na teplotě [m²‧s⁻¹].

Rovněž je zapotřebí stanovit součinitel přestupu tepla α_e. Výpočet je uveden ve vztahu (3) a vychází z odborné literatury [6].

(3)

kde je

α_e: součinitel přestupu tepla na povrchu izolace [W‧m⁻²‧K⁻¹],
α_k: součinitel přestupu tepla konvekcí na povrchu izolace [W‧m⁻²‧K⁻¹],
α_r: součinitel přestupu tepla radiací na povrchu izolace [W‧m⁻²‧K⁻¹],
t₁: teplota kapaliny v daném úseku potrubí [°C],
t₂: teplota okolního vzduchu v daném úseku potrubí [°C],
T₁: absolutní teplota hodnoty t₁ [K],
T₂: absolutní teplota hodnoty t₂ [K],
D_iz: vnější průměr izolace [m],
C: součinitel sálání potrubí nebo povrchu izolace [W‧m⁻²‧K⁻⁴].

Použijeme-li vstupní parametry z kapitoly 2.2 na vztahy (1) až (3) získáme výsledky, které uvádí tabulka 1. Při výpočtu veličin U, α_i a α_e se uvažovalo se zjednodušeným předpokladem. A to s teplotou teplonosné kapaliny t₁ = 50 °C (průměrná teplota), s teplotou okolního prostředí t₂ = 20 °C.

Tab. 1 Výsledky tepelně technických parametrů potrubí solárního okruhu
`α`_i [W‧m⁻²‧K⁻¹]	`α`_e [W‧m⁻²‧K⁻¹]	`U` [W‧m⁻²‧K⁻¹]
911,751	9,446	0,158

V dalším kroku se stanoví měrná tepelná ztráta potrubí q_p. Tuto hodnotu je nutné zadat jako vstupní údaj do simulace. Nejprve vypočteme ztrátu potrubí Q_p na délku l = 1 m.

(4) [W‧m⁻¹‧K⁻¹]

Pak je možné vypočíst měrnou tepelnou ztrátu q_p na ploše jeden metr čtvereční potrubí při teplotním rozdílu 1 K.

(5) [W‧m⁻²‧K⁻¹]

Měrná ztráta q_p bude použita v simulaci s tím, že teploty v okolí potrubí budou vycházet z reálných klimatických dat pro exteriér, pro interiér byla zvolena celoročně teplota 20 °C.

3. Výsledky

Na modelu solární teplovodní soustavy vytvořeném v energetickém simulačním nástroji TRNSYS byly provedeny simulace s implementováním komponentu potrubí. Zvoleny byly délky n 0 až 10 m, s roztečí po jednom m. Hodnota 0 m délky potrubí je pouze teoretická (v praxi nereálná). Ve výpočtu byla zvolena pouze za účelem lepší demonstrace vlivu tepelné ztráty potrubí. Skutečná délka potrubí soustavy je hodnota n uvedená v tabulce 2, která je vynásobena čtyřmi. Protože soustava obsahuje celkem čtyři úseky potrubí: 2 potrubí v interiéru (l_ip, l_iv) a 2 potrubí v exteriéru (l_ep, l_ev), viz obrázek 1.

Nejzajímavější výsledek simulace je uveden v tabulce 2. V této tabulce jsou uvedeny tepelné ztráty potrubí pro zvolené délky potrubí n. V dalším řádku pak využitelné solární zisky se zahrnutím vlivu tepelných ztrát potrubím.

Tab. 2 Tepelná ztráta potrubí pro jednotlivé délky potrubí `l`_ip, `l`_iv, `l`_ep, `l`_ev
Délka potrubí `n` [m]	0	1	2	3	4	5	6	7	8	9	10
Ztráta potrubím [kWh‧rok⁻¹]	0	33	66	99	131	164	197	236	263	295	328
Využitelné teplo solární soustavy [kWh‧rok⁻¹]	1501	1468	1435	1402	1370	1337	1304	1265	1238	1206	1173
Podíl tepelné ztráty potrubím [%]	0	2,2	4,4	6,6	8,7	11,0	13,1	15,7	17,5	19,7	21,9

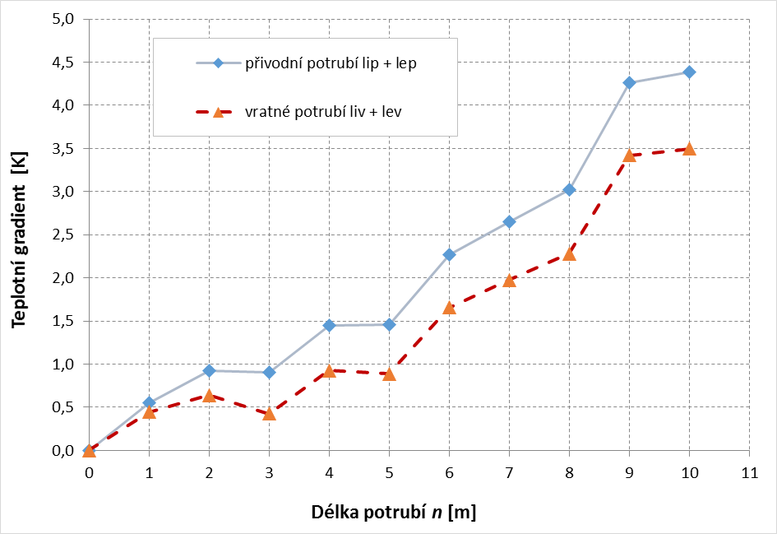
Dalším výsledkem je průběh poklesu teploty kapaliny vzhledem k délce úseku potrubí, který je graficky znázorněn na obrázku 2. Konkrétně je zde znázorněn průběh simulace pro 21. červenec ve 12:00. Patrná je lineární závislosti mezi délkou potrubí a poklesem teploty. Pro ostatní dny a časy mají výsledky podobný charakter. Zajímavý je největší teplotní rozdíl z celého pásma délek, a to konkrétně mezi vzdálenosti potrubí n = 8 a n = 9 metrů.

Obr. 2 Teplotní gradient tepelné ztráty potrubím pro den 21. 7. v čase 12:00

4. Závěr

Výsledky výpočtů tepelné ztráty potrubím uvedené v článku se vztahují k simulaci solární soustavy, která obsahuje dva deskové kolektory a zásobuje TV objekt obývaný čtyřmi osobami. Závěry z výsledků je možné s jistou dávkou opatrnosti přenést i na jiné podobné solární soustavy. Tepelné ztráty potrubí v jiných případech instalací však budou nabývat vyšších či nižších hodnot v závislosti na skutečné velikosti soustavy, délkách a rozměrech potrubí.

Tepelné ztráty potrubím mají vliv na celkovou energetickou bilanci solární soustavy. Při provedení kvalitní tepelné izolace však tento vliv není příliš významný u běžných délek potrubí. Při maximální délce potrubí při (n = 10) 40 m, při kterých proběhla simulace, byla ztráta tepelné energie 21,9 % při dané konfiguraci simulace a solární soustavy. Běžné délky potrubí pro zadanou solární soustavu, bývají zhruba do 20 m (n = 5). V takovém případě je tepelná ztráta potrubím 11 % využitelné energie solární soustavy. Což sice není vysoké číslo, ale uvážlivý investor a projektant by tuto skutečnost měli vzít v potaz při návrhu solární soustavy. Zvláště s ohledem na postupný přechod k budovám s téměř nulovou spotřebou energie. V tomto standartu budou muset být všechny nové budovy od roku 2020.

Na tepelnou ztrátu potrubím u solárních soustav má největší vliv potrubí, které vede v exteriéru. Cílem návrhu by proto mělo být, aby potrubí v exteriéru bylo pokud možno co nejkratší, aby byly tyto tepelné ztráty eliminovány.

Poděkování

Tento článek byl vytvořen za podpory projektu: Podunajská spolupráce DS-2016-0030 Energy efficiency and indoor environment of nearly zero energy building; Specifický výzkum VUT Brno FAST-S-18-5217.

Literatura

TNI 73 0302. Energetické hodnocení solárních tepelných soustav – Zjednodušený výpočtový postup. 2014
Internetový portál: http://www.trnsys.com/
Internetový portál: https://www.tzb-info.cz/tabulky-a-vypocty/36-medene-trubky
Internetový portál: https://www.tzb-info.cz/tabulky-a-vypocty/37-hodnoty-fyzikalnich-velicin-vybranych-kovu
Vyhláška č. 193/2007 Sb., kterou se stanoví podrobnosti účinnosti užití energie při rozvodu tepelné energie a vnitřním rozvodu tepelné energie a chladu
Ráž, J. V. Izolace potrubí podle evropských doporučení. TZB-info. ISSN 1801-4399. 2011. URL:
https://vytapeni.tzb-info.cz/normy-a-pravni-predpisy-vytapeni/7459-izolace-potrubi-podle-evropskych-doporuceni

English Synopsis

Influence of heat loss of the pipeline on the energy balance of the solar system

The paper deals with the analysis of thermal losses of pipe distributions in the small solar system model created in the TRNSYS energy simulation tool. Attention is paid to the impact of heat loss through pipelines on the overall energy balance. Several variants of pipe lengths for one type of system have been selected. The results presented in the articles illustrate the influence of different pipe lengths on heat losses and the consequent impact on the energy balance of the monitored system.