Reklama

Metodika pro odhad teplotního faktoru vnitřního povrchu v oblasti zasklívací spáry

18.5.2015

Ing. Roman Jirák, Ph.D., Decoen v.o.s.

Recenzovaný

Reklama

Povrchová teplota jako jeden z nejsledovanějších parametrů otvorových výplní a lehkých obvodových plášťů nejen v České republice posuzuje konstrukce z pohledu rizika kondenzace vodních par resp. z pohledu jejich zdravotní a hygienické závadnosti či nezávadnosti vzhledem k prostředí, do kterých jsou zabudovávány. Jeho smyslem je určení, zdali daná konstrukce je vhodná pro konkrétní okrajové podmínky, nebo je nutné zvolit konstrukci odlišnou.

Jak již bylo zmíněno v jednom z předchozích článků [1], majoritní odpovědnost by měl nést za vhodný návrh např. okenních konstrukcí především projektant. Ten je seznámen jak s potřebami investora, tak s lokalitou a navrhovaným objektem samotným a má tedy všechny informace pro to, aby požadavky na vybrané a následně zabudované otvorové výplně stanovil. Pokud toto všechno je řádně provedeno přichází na řadu stavebník ať už z pozice výrobce, stavební firmy nebo developera. Ten musí vybrat dodat vhodnou konstrukci podle předešlých požadavků tak, aby např. ke zmiňovanému problému s kondenzací vodních par a následnému vzniku plísní nedocházelo. Ověření této skutečnosti není však rutinní záležitostí ať už se jedná o způsob experimentální nebo o cestu výpočtu ve dvourozměrném teplotním poli.

Předkládaný článek byl iniciován situací týkající se otvorových výplní ve stavebnictví v České republice. Projektanti, projekční firmy a obzvláště developeři vybírají otvorové výplně především podle ceny. Kvalita bohužel při výběrových řízeních nehraje majoritní roli, přestože při výběru nekvalitních výplní nejen do velkých developerských projektů se vystavují značnému riziku zvolení nevhodných konstrukcí, které zpravidla mívá za následek další investici na opravy, popřípadě na výměnu oken. O tom, že k této situaci dochází, svědčí časté soudní spory. Firmy bohužel neinvestují do expertíz nebo posudků, které by jim zaručily správný výběr konstrukce do dané lokality a objektu, přestože z dlouholetých zkušeností vyplývá, že je méně nákladné vyhotovení posudků než případné opravy. Na druhé straně projektanti menších objektů, jako jsou například rodinné domy, popřípadě investoři, si ve velké většině nemohou, nebo nechtějí takovýto posudek dovolit.

Jedním z cílů článku je pomoc zlepšit informovanost na českém trhu. Proto se tento článek zabývá vývojem metodiky, která by stanovila kvalitu konstrukce z pohledu kondenzace vodních par, a mohla tak projektantovi pomoci, bez složitých a nákladných výpočtů, vybrat vhodnou okenní konstrukci pro zabudování do daného objektu. Vzhledem k výsledkům experimentálních měření a matematicko-numerických simulací publikovaných předcházejících článků [1] je nutné metodiku zaměřit na oblast zasklívací spáry v charakteristickém průřezu a v dalších publikacích i na oblast rohu zasklívací jednotky.

Vývoj metodiky pro stanovení `f`_Rsi na charakteristickém průřezu rámu

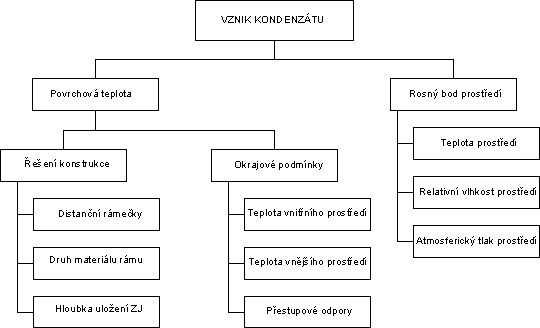
Obrázek č. 1 Blokové schéma prvků ovlivňujících vznik kondenzace vodních par v oblasti zasklívací spáry

Aby bylo možné výše zmíněný záměr realizovat, musí být nejdříve stanoveny jednotlivé prvky, které vhodnost konstrukce určují. Pokud se na problematiku podíváme z výzkumného hlediska a na chvíli opomeneme normové předpisy, ke kterým se vzápětí vrátíme, můžeme vytvořit následující schéma. Schéma nám pomůže stanovit krok po kroku jednotlivé prvky, které budou ovlivňovat vhodnost dané konstrukce pro zabudování do konkrétních podmínek. Obrázek č. 1 řadí v návaznosti do blokového schématu jednotlivé prvky, které ovlivňují, zda ke kondenzaci bude, nebo nebude docházet. Aby ke kondenzaci nedocházelo, musí být povrchová teplota konstrukce vyšší než rosný bod daného prostředí. Rosný bod je určen teplotou (θ_ai), relativní vlhkostí (w) a atmosférickým tlakem. V praxi se jedná o druh vnitřního prostředí, do něhož konstrukci osazujeme. Tuto informaci stanovuje ČSN 730540 – 3 [2], ve které jsou deklarovány návrhové podmínky pro jednotlivé druhy místností. Dále je hodnota povrchové teploty ovlivňována konkrétním řešením konstrukce a okrajovými podmínkami. Z okrajových podmínek se jedná o teplotu vnitřního prostředí (θ_ai), teplotu vnějšího prostředí (θ_e) a přestupové odpory na vnitřní a vnější straně (R_si, R_se). Hodnoty těchto parametrů jsou opět stanoveny normami. Konstrukční řešení, tedy prvky, které nejvíce ovlivňují povrchovou teplotu v oblasti zasklívací spáry, vychází výsledků výzkumu publikovaných v [4] a [5].

Je nutné podotknout, že blokové schéma obsahuje určitá zjednodušení. Problém je velice komplexní a nelze analyzovat všechny faktory mající na vznik kondenzátu vliv. Zjednodušení byla stanovena tak, aby nejméně ovlivňovala výstup, nebo se pohybovala na straně bezpečnosti. Ze zkušeností je například známé, že izolační trojskla vykazují při stejných podmínkách a konstrukčních zásadách vyšší vnitřní povrchovou teplotu v oblasti zasklívací spáry. Dále teplotu ovlivňují i různá složení zasklívacích jednotek i hodnoty součinitelů prostupu tepla. Zahrnutí všech těchto a dalších vlivů by analýzy mnohonásobně zkomplikovalo tak, že by dosažení užitných závěrů bylo nereálné.

Aby byla metodika použitelná i pro projektanty bez hlubokých znalostí o transportu tepla a ověřování rizika kondenzace vodních par na okenních konstrukcích, nesmí vyžadovat velké množství vstupů a zároveň je nutné, aby nezávisela na neomezeném množství proměnných. Rosný bod, resp. minimální požadovaný teplotní faktor vnitřního povrchu pro dané prostředí, vychází z normy. Zbývá nám stanovit minimální teplotu na vnitřním povrchu konstrukce. Vliv okrajových podmínek lze eliminovat použitím jako výstupu místo povrchové teploty teplotního faktoru vnitřního povrchu, který není závislý na okrajových podmínkách. Tato bezrozměrná veličina určuje vlastnost konstrukce v daném bodě a pro stejnou konstrukci má vždy neměnnou hodnotu, ať konstrukci vystavíme jakýmkoli okrajovým podmínkám. Vztah teplotního faktoru k okrajovým podmínkám charakterizují následující rovnice [3].

Na další rovnici je odvozeno předcházející tvrzení, že teplotní faktor je lokální charakteristickou vlastností konstrukce a není závislý na okrajových podmínkách.

f_Rsi = 1 − U_x . R_si

Pro obě rovnice platí:

θ_ai: … návrhová teplota vnitřního prostředí [°C]
θ_e: … návrhová teplota vnějšího prostředí [°C]
θ_si: … povrchová teplota v daném místě [°C]
U_x: … lokální součinitele prostupu tepla v místě θ_si [W/m²K]
R_si: … přestupový odpor v místě θ_si [m²K/W]
f_Rsi: … teplotní faktor vnitřního povrchu [–]

Po eliminaci vlivu okrajových podmínek zbývá už jen stanovit řešení posuzované konstrukce. Charakteristické prvky konstrukce, které ovlivňují vnitřní povrchovou teplotu, potažmo teplotní faktor vnitřního povrchu, byly analyzovány v průběhu výzkumu jehož výsledky byly publikovány [4] [5]. Zde byla uvedena systematická řada výpočtů pro všechny kombinace těchto faktorů (hloubka uložení zasklívací jednotky, tři druhy materiálů okenního rámu a devět druhů distančních rámečků). Mezi těmito faktory lze najít určitou závislost. V následující tabulce č. 1 jsou vidět výsledky kombinací dvou distančních rámečků. Kompletní výsledky výpočtů nejsou publikovány. V tabulce jsou zobrazeny výsledky pro každou kombinaci vypočtené vnitřní povrchové teploty a jejich přepočet na teplotní faktor vnitřního povrchu pomocí předcházejícího vzorce s dosazením okrajových podmínek výpočtu (θ_ai = 21 °C, θ_e = −15 °C). Teplotní faktor pro konkrétní hloubku uložení, materiál okenního rámu a druh distančního rámečku budou vždy stejné, ať konstrukci umístíme do jakékoliv lokality. Protože není možné disponovat s množstvím všech kombinací, je možné využít skutečnosti, že každý distanční rámeček vykazuje v kombinaci s daným typem rámu závislost mezi hloubkou uložení a teplotním faktorem. Tato závislost pro kombinace dřevěného okenního rámu a distančních rámečků uvedených v tabulce je vynesena do grafu č. 1. Pro stanovení nejpravděpodobnější závislosti je proložena křivkou polynomická spojnicá trendu druhého řádu. Přestože by průběh, který reprezentuje hodnoty dat, charakterizovala spíše logaritmická funkce, u které data rychle stoupají nebo klesají a postupně se vyrovnávají, je vhodnější použít pro omezený počet možných hloubek uložení polynomickou funkci.

Tabulka č. 1 výsledky výpočtů povrchových teplot a teplotních faktorů
Druh distančního rámečku	Plastový rám			Dřevěný rám			Hliníkový rám

	Hloubka uložení [mm]	`θ`_si [°C]	`f`_Rsi [–]	Hloubka uložení [mm]	`θ`_si [°C]	`f`_Rsi [–]	Hloubka uložení [mm]	`θ`_si [°C]	`f`_Rsi [–]
Aluminium Spacer Bar Bentable	15	6,36	0,593	15	4,02	0,528	15	6,67	0,602
	16	6,83	0,606	16	4,67	0,546	16	7,24	0,618
	17	7,28	0,619	17	5,33	0,565	17	7,71	0,631
	18	7,69	0,630	18	5,81	0,578	18	8,17	0,644
	19	8,06	0,641	19	6,35	0,593	19	8,58	0,655
	20	8,43	0,651	20	6,78	0,605	20	8,96	0,666
	21	8,75	0,660	21	7,23	0,618	21	9,33	0,676
	22	9,07	0,669	22	7,64	0,629	22	9,60	0,683
	23	9,35	0,676	23	8,00	0,639	23	9,94	0,693
	24	9,63	0,684	24	8,33	0,648	24	10,20	0,700
	25	9,89	0,691	25	8,64	0,657	25	10,46	0,707
Swisspacer V	15	10,80	0,717	15	10,2	0,701	15	11,46	0,735
	16	11,00	0,722	16	10,39	0,705	16	11,74	0,743
	17	11,16	0,727	17	10,66	0,713	17	11,92	0,748
	18	11,33	0,731	18	10,76	0,716	18	12,09	0,753
	19	11,47	0,735	19	10,92	0,720	19	12,26	0,757
	20	11,63	0,740	20	11,08	0,724	20	12,40	0,761
	21	11,77	0,744	21	11,23	0,729	21	12,52	0,764
	22	11,89	0,747	22	11,36	0,732	22	12,62	0,767
	23	12,02	0,751	23	11,50	0,736	23	12,73	0,770
	24	12,16	0,754	24	11,62	0,739	24	12,82	0,773
	25	12,25	0,757	25	11,73	0,743	25	12,91	0,775

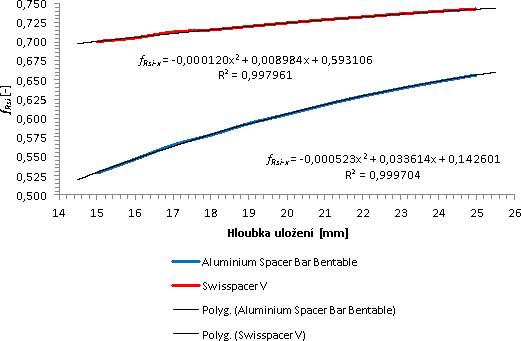
Graf č. 1 Stanovení rovnice závislosti hloubky uložení zasklívací jednotky na teplotním faktoru

Pro spojnici trendu již není problém stanovit rovnici regrese. Ta je matematickým vyjádřením závislosti teplotního faktoru vnitřního povrchu na hloubce uložení zasklívací jednotky, která platí pro danou kombinaci distančního rámečku a druhu okenního rámu. Míru přesnosti spojnice a její rovnice určuje tzv. koeficient spolehlivosti R zobrazený v grafu pod rovnicí. Čím více se hodnota blíží 1, tím je rovnice přesnější. Jak je vidět, rovnice jsou zatížené minimální chybou. Pro takovýto případ je i určitá malá nepřesnost žádoucí, protože pak mohou být křivkou eliminovány určité malé odchylky, které vznikly nepřesností výpočtů (např. problematika sítě) nebo zaokrouhlováním postupných výsledků. Pro ověření přesnosti rovnice byl proveden následující příklad:

pro závislost mezi hloubkou uložení a teplotním faktorem byla stanovena následující rovnice závislosti, kde x [mm] je hloubka uložení zasklívací jednotky. Pro ověření je dosazena hloubka uložení 16 mm, 19 mm a 23 mm.

f_Rsi–x = 0,000523x² + 0,033614x + 0,142601

f_Rsi–16 = 0,5465
f_Rsi–19 = 0,5924
f_Rsi–23 = 0,6390

Výsledky výpočtů a jejich porovnání s výpočtem ve dvourozměrném teplotním poli jsou zaneseny v následující tabulce č. 2:

Tabulka č. 2 porovnání výsledků výpočtu z rovnice a výsledků výpočtu z dvourozměrného teplotního pole
Hloubka uložení `x` [mm]	`f`_Rsi–x [–]			`θ`_si [°C]
Hloubka uložení `x` [mm]	rovnice	výpočet 2`D`	Δ`f`_Rsi	rovnice	výpočet 2`D`	Δ`θ`_si
16	0,5465	0,5464	0,0001	4,67	4,67	0,00
19	0,5924	0,5931	0,0007	6,33	6,35	0,02
23	0,6390	0,6389	0,0001	8,00	8,00	0,00

Rozdíly mezi vypočteným teplotním faktorem z uvedené rovnice a z výpočtu ve dvourozměrném teplotním poli jsou odlišné až na čtvrtém desetinném místě. Tato nepřesnost je v rámci tolerance zaokrouhlování teplotního faktoru. Pro větší přehled jsou zobrazeny rozdíly ve °C. Největší odchylku vykázala hloubka 19 mm. A to pouze 0,02 °C. Z výsledku uvedených příkladů je patrné, že rovnice popisuje křivku s dostatečnou přesností. Rovnice je tedy možné použít při empirickém stanovení teplotního faktoru vnitřního povrchu pro danou kombinaci v závislosti na hloubce uložení zasklívací jednotky.

Zásadním výstupem je tabulka č. 3, kde je uvedeno 6 rovnic reprezentujících jednotlivé konkrétní kombinace druhu materiálů okenního rámu a druhu distančních rámečků. Jejich řešením je možné stanovit odhad teplotního faktoru. Ke každé rovnici je uveden i koeficient spolehlivosti. Ve velké většině koeficient přesahuje hodnotu 0,999. Tato hodnota poukazuje na vysokou přesnost, kterou spojnice reprezentuje danou křivku.

Tabulka č. 3 rovnice pro odhad teplotního faktoru vnitřního povrchu
Distanční rámeček	Rovnice	Spolehlivost	Druh rámu
Aluminium Spacer Bar Bentable	`f`_Rsi–x = −0,000332`x`² + 0,023024`x` + 0,323157	`R`² = 0,999903	Plastový
	`f`_Rsi–x = −0,000532`x`² + 0,033614`x` + 0,142601	`R`² = 0,999704	Dřevěný
	`f`_Rsi–x = −0,000436`x`² + 0,027820`x` + 0,283662	`R`² = 0,999690	Hliníkový
Swisspacer V	`f`_Rsi–x = −0,000105`x`² + 0,008221`x` + 0,617298	`R`² = 0,999655	Plastový
	`f`_Rsi–x = −0,000120`x`² + 0,008984`x` + 0,593106	`R`² = 0,997961	Dřevěný
	`f`_Rsi–x = −0,000227`x`² + 0,012960`x` + 0,592753	`R`² = 0,998279	Hliníkový

Rovnice pro kombinace ostatních sedmi druhů rámečků pro jednotlivé druhy materiálů okenních rámů zde nejsou publikovány. Výpočty všech analyzovaných distančních rámečků a kombinací ostatních faktorů je možné provést ve veřejné internetové aplikaci na stránkách www.decoen.cz/frsi. Ukázka aplikace pro výpočet teplotního faktoru vnitřního povrchu v oblasti zasklívací jednotky na charakteristickém průřezu rámu je zobrazena na následujícím obrázku č. 2. [6]

Obrázek č. 2 Ukázka aplikace pro odhad teplotního faktoru vnitřního povrhu na charakteristickém průřezu rámu

Validace metodiky

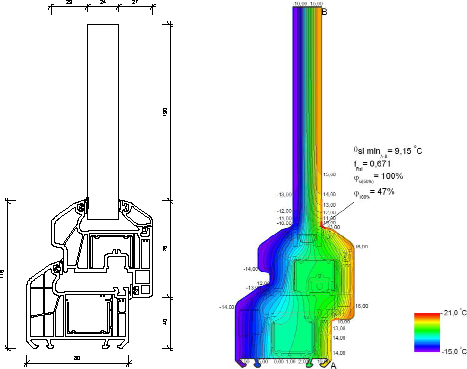
Obrázek č. 3 Příkladný výstup výpočtu a profilace

Jestli je možné použít v praxi odvození teplotního faktoru vnitřního povrchu dle předcházející metodiky, která vychází ze tří hlavních faktorů, je nutné ověřit její validací. Validace může odhalit, zda je použití druhu rámu, druhu distančního rámečku a hloubky uložení zasklívací jednotky jako majoritních faktorů dostačující pro odhad povrchové teploty. Pro ověření byla zvolena skupina profilů pohybujících se na evropském trhu, avšak odlišných, než byly použity v předešlých případech. Charakteristický řez profilu a jeho grafický výstup z výpočtu ve dvourozměrném teplotním poli programu Flixo jsou zobrazeny na obrázku č. 3. Výsledky výpočtů v porovnání s výsledky vypočtenými dle uvedených rovnic shrnuje následující tabulka č. 4

Tabulka č. 4 výsledky ověření metodiky pro stanovení teplotního faktoru vnitřního povrchu
č. okenního profilu	Materiál rámu	Distanční rámeček	Hloubka uložení ZJ [mm]	Rovnice	Výpočet ve 2D teplotním poli		Odhad pomocí rovnice		Odchylky		Nepřes- nost [%]
č. okenního profilu	Materiál rámu	Distanční rámeček	Hloubka uložení ZJ [mm]	Rovnice	`fR`_si [–]	`θ`_si [°C]	`fR`_si [–]	`θ`_si [°C]	Δ`fR`_si [–]	Δ`θ`_si [°C]	Nepřes- nost [%]
1	hliník	Chromatec	15	`f`_Rsi–x = −0,000341`x`² + 0,021003`x` + 0,422879	0,669	9,10	0,661	8,80	−0,008	−0,30	−1,20
1	hliník	Swisspacer V	15	`f`_Rsi–x = −0,000227`x`² + 0,012960`x` + 0,592753	0,736	11,50	0,736	11,50	0,000	0,00	0,00
2	plast	TGI	15	`f`_Rsi–x = −0,000181`x`² + 0,013100`x` + 0,519470	0,671	9,15	0,675	9,30	0,004	0,15	0,60
2	plast	Swisspacer V	13	`f`_Rsi–x = −0,000105`x`² + 0,008221`x` + 0,617298	0,703	10,32	0,706	10,43	0,003	0,11	0,48
2	plast	TGI (bez výztuhy)	15	`f`_Rsi–x = −0,000181`x`² + 0,013100`x` + 0,519470	0,673	9,23	0,675	9,30	0,002	0,07	0,30
2	plast	Swisspacer V	15	`f`_Rsi–x = −0,000105`x`² + 0,008221`x` + 0,617298	0,714	10,72	0,717	10,81	0,003	0,09	0,42
3	dřevo-hliník	Swisspacer V	15	`f`_Rsi–x = −0,000120`x`² + 0,008984`x` + 0,593106	0,712	10,62	0,701	10,24	−0,011	−0,38	−1,54
4	plast	Aluminium bendable	21	`f`_Rsi–x = −0,000332`x`² + 0,023024`x` + 0,323157	0,658	8,69	0,660	8,76	0,002	0,07	0,30
4	plast	Swisspacer	15	`f`_Rsi–x = −0,000164`x`² + 0,012674`x` + 0,517197	0,669	9,09	0,670	9,12	0,001	0,03	0,15
5	dřevo	Thermix TX.N	12	`f`_Rsi–x = −0,000197`x`² + 0,013899`x` + 0,495455	0,632	7,74	0,634	7,82	0,002	0,08	0,28
6	hliník	Chromatec Plus	15	`f`_Rsi–x = −0,000285`x`² + 0,018422`x` + 0,455859	0,684	9,64	0,668	9,05	−0,016	−0,59	−2,34
6	hliník	Chromatec Ultra	15	`f`_Rsi–x = −0,000243`x`² + 0,014819`x` + 0,540783	0,719	10,87	0,708	10,50	−0,011	−0,37	−1,48
6	hliník	Chromatec Ultra	17	`f`_Rsi–x = −0,000243`x`² + 0,014819`x` + 0,540783	0,739	11,59	0,722	11,01	−0,017	−0,58	−2,24

První část tabulky obsahuje označení okenního profilu a kombinaci faktorů s patřičnou rovnicí odvozenou pro odhad povrchové teploty. Dále jsou uvedené výsledky jak odhadu pomocí rovnice, tak i výpočet ve dvourozměrném teplotním poli. Odchylky mezi výpočtem a vyvinutou rovnicí jsou umístěny v pravé části tabulky. Nepřesnost porovnávaných výpočtů je v průměru 0,87 % a průměrná odchylka povrchových teplot 0,22 °C. Nepřesnosti jsou zapříčiněny především odlišnou geometrií rámů a jejich konstrukčním řešením, které nejsou zahrnuty v analyzovaných faktorech ovlivňujících povrchovou teplotu v oblasti zasklívací spáry.

Relativně velká přesnost metody odhadu teplotního faktoru, resp. vnitřní povrchové teploty v oblasti zasklívací spáry na charakteristickém průřezu rámu, poukazuje na skutečnost, že analyzované faktory v předcházející kapitole představují majoritní prvky mající na vnitřní povrchovou teplotu vliv. Je nutné však podotknout, že tyto faktory nejsou jediné, které danou problematiku ovlivňují. Existuje celá řada vedlejších faktorů, které díky jejich velkému počtu nelze do odhadů jednoduše zahrnout. Jedná se například o řešení funkční spáry. Zdali funkční spára obsahuje středové těsnění, nebo pouze dorazové. Je-li u dřevěné okenní konstrukce použita okapnice s přerušeným tepelným mostem, nebo je okapnice celá z hliníku. Jestli je do zasklívací spáry u hliníkových konstrukcí aplikován izolační materiál, nebo EPDM těsnění rozdělující dutinu zasklívací spáry a mnoho dalších.

Při ověření míry přesnosti metodiky odhadu povrchové teploty, resp. teplotního faktoru v oblasti zasklívací spáry na charakteristickém průřezu rámu je zřejmé, že tímto postupem nelze plnohodnotně nahradit samotné výpočty. Je ji však možné použít pro stanovení užšího výběru konstrukcí, které budou vhodné pro zabudování do daného objektu, a může tak být značně nápomocna jednotlivým projektantům. V praxi může napomoci předejít problémům s narušováním zdravotní a hygienické nezávadnosti obytných prostředí, které se stále často objevují.

Závěr

Cílem článku bylo aplikovat výsledky předchozích analýz a experimentů a najít mezi nimi matematickou závislost, pomocí které by bylo možné stanovit teplotní faktor vnitřního povrchu na okenních konstrukcích v jejich kritických místech, a do určité míry jimi nahradit složité dvourozměrné a trojrozměrné výpočty. Z validací vyplývá, že jednotlivé metodiky mohou sloužit pro odhad teplotního faktoru vnitřního povrchu, a značně tak v praxi napomoci projektantům a architektům při výběru otvorových výplní do daného objektu, ale není možné jimi plnohodnotně nahradit výpočty ve dvourozměrných a trojrozměrných teplotních polích. Z článku plynou následující hlavní závěry:

byly vytvořeny rovnice pro odhad teplotního faktoru vnitřního povrchu f_Rsi–x na charakteristickém průřezu rámu v zasklívací spáře v závislosti na hloubce uložení zasklívací jednotky, a to pro kombinace devíti druhů distančních rámečků a tří základních materiálů okenních rámů;
byla vytvořena veřejná internetová aplikace využívající předcházející výstupy matematicko-numerických simulací a experimentálních měření dostupná na www.decoen.cz/frsi. Jejím cílem je pomoc při navrhování otvorových výplní projektantům, investorům, developerům a dalším.

Zdroje

[1] R. JIRÁK, Současné otvorové výplně na českém a evropském trhu II – Nejkritičtější místa z pohledu kondenzace vodních par na vnitřním povrchu, Materiály pro stavbu 3/2013, str. 21–25.
[2] ČSN 730540-3: Tepelná ochrana budov Část 3: Návrhové hodnoty veličin. Praha: ČNI 2005
[3] J. ŠÁLA, Teplotní faktor vnitřního povrchu f_Rsi pro ČSN 730540-2, Tepelná ochrana budov, 4/2006
[4] R. JIRÁK, Současné otvorové výplně na českém a evropském trhu III A – Analýza faktorů ovlivňujících povrchovou teplotu v oblasti zasklívací spáry, Materiály pro stavbu 4/2013, str. 16–19.
[5] R. JIRÁK, Současné otvorové výplně na českém a evropském trhu III B – Analýza faktorů ovlivňujících povrchovou teplotu v oblasti zasklívací spáry, Materiály pro stavbu 5/2013, str. 18–21.
[6] www.decoen.cz/frsi

Ing. Roman Jirák, Ph.D. (*1982)

je soudním znalcem v oboru stavebnictví se specializací na otvorové výplně a tepelnou techniku lehkých obvodových plášťů. Absolvoval doktorské studium na ČVUT Fakultě stavební v Praze. Dva roky pracoval jako tepelný technik ve společnosti Skanska v závodě lehkých obvodových plášťů. Po té strávil čtvrt roku na pracovní stáži v IFT Rosenheim v Německu, kde se soustředil na simulaci transportu tepla skrz LOP a otvorové výplně. V současné době řídí společnost DECOEN v.o.s. zaměřující se na tepelnou techniku a na snižování energetické náročnosti budov.

English Synopsis

The methodology for estimation of the thermal factor at the inner surface in the area of glazing groove

The surface temperature as one of the most watched parametres of the opening panes and light enveopes not only in the Czech Republic is being assessed in a view of risk of water vapour condensation, or more precisely in a view of their health and a hygyenic flaws and ecologically sound environment where inbuilt. The mening is determination if the structure is suitable for the marginal conditions or whether is necessary to choose another structure.