Reklama

Empirické modely charakteristik výbuchů a požárů a jejich scénáře

Ing. Otto Dvořák, Ph.D., VŠB TUO FBI Ostrava, externí školitel

Recenzovaný

Příspěvek shrnuje scénáře havarijních úniků plynů a kapalin. Jejich nebezpečí dokládá statistikou požárů od výbuchů v ČR za období 2012–2019. Dále uvádí empirické modely vybraných charakteristik fyzikálních a chemických výbuchů uniklých plynů a kapalin. Příspěvek je doplněn příkladem výpočtu. Na tento článek navazuje další text s názvem „Empirické modely charakteristik nebezpečí výbuchů a požárů, odhad charakteristik a kategorizace staveb“, který přináší kromě jiného i podrobné závěrečné shrnutí.

Reklama

Úvod

Když hořlavé látky havarijně uniknou z potrubí, nádrže, nádob, cisterny, provozního zařízení mohou nastat různé scénáře nebezpečí v závislosti zejména na jejich chemickém složení, skupenství (zda jde o plyn, kapalinu nebo o obě fáze), dále na jejich tlaku, teplotě a době iniciace od počátku úniku a v neposlední řadě na vzdálenostech a druzích sousedních objektů. Tyto scénáře lze blíže specifikovat při havarijním úniku:

hořlavých plynů jako:
- výbuch fyzikální nebo chemický,
- požár/vzplanutí,
- tryskový požár,
hořlavých kapalin nebo zkapalněných plynů jako:
- požár kaluže,
- ohnivá koule,
- požár vytékající kapaliny.

Že je nebezpečí od těchto scénářů v České republice stále reálné lze doložit např. následující tab. 1 a obr. 1.

Tab. 1 Požáry od výbuchů s únikem NCHL v ČR [1]
požáry od výbuchů	Σ `V`	Σ `U`	Σ `Z`	Σ `PŠ` [tis. Kč]
2012	18	1	21	9 961
2013	14	0	55	102 778
2014	12	2	20	9 598
2015	17	1	40	658 732
2016	14	2	15	8 212
2017	11	0	51	54 807
2018	4	0	2	1 422
2019	11	0	14	10 550
Průměr	12,625	0,75	27,25	107 007,5

Obr. 1 Celkové počty požárů a U a Z osob v ČR způsobených výbuchy HK, HP, HPR [2]

Vysvětlivka: V = výbuchy, U = usmrceno, Z = zraněno osob, PŠ = přímé škody, Σ = suma, NCHL = nebezpečné chemické látky, HK = hořlavé kapaliny, HP = hořlavé plyny, HPR = hořlavé prachy.

Výbuchy a požáry vyšetřuje Policie ČR a HZS ČR ke zjištění jejich příčin, škod a postižení případných viníků. Tak tomu bylo i u výbuchu a následném požáru např. v Chemických závodech v Záluží u Mostu, který se stal 19. července 1974 ve výrobně lihu. Výrobní dispečer zpozoroval ve 20:09 hodin únik etylénu z potrubí, zavolal hasiče, ale vzápětí se ozval ohlušující výbuch s následným požárem, se kterým bojovalo 22 jednotek PO s 200 hasiči více než čtyři dny. Vyšetřovatelé HZS a PČR zjistili, že plyn unikal z kolena etylenového potrubí, které mělo korozí zeslabenou 6mm stěnu natolik, že ji přetlak uvnitř potrubí protrhl. Unikající etylén se promísil se vzduchem a vzniklý oblak zapálil plamen přilehlé pece. Síla výbuchu byla odhadnuta na sílu výbuchu 25 t TNT. Tlaková vlna výbuchu srovnala se zemí část chemičky a poničila 313 dalších objektů v okolí, z toho 220 rodinných domů až do vzdálenosti 8 km. Na opravu všech rozbitých oken bylo zapotřebí 80 vagonů skla. Celková škoda byla několik miliard korun a celkem bylo usmrceno 17 osob a zraněno 112 osob. Hodně obětí bylo i v projíždějící tramvaji, u které žár výbuchu a požáru roztavil skleněné výplně.

Na výbuších s následným požárem se podílejí kromě chemických provozů též obytné a rodinné domy, administrativní budovy, skladovací objekty, dopravní prostředky využívající hořlavé plyny nebo kapaliny.

Ze souhrnných čísel tab. 1 a grafu obr. 1 je patrno, že trendy počtu U a Z osob a přímých škod od požárů způsobených výbuchy za sledované období jsou klesající, nicméně jejich hodnoty si vynucují věnovat zvýšenou pozornost při posuzování rizik možných havárií a upřesňování potřebných preventivních opatření.

K tomu jsou potřebné též výpočetní odhady mimo jiné výbuchových tlaků a energie generované výbuchy havarijně uniklých plynů a hořlavých kapalin, a intenzita sálání a výška plamenů požárů. V průmyslu pro hodnocení jejich rizik jsou jednoduše aplikovatelné tzv. empirické modely odvozené korelací z experimentálních dat. Modely uvedené v tomto článku nejsou jejich úplným výčtem.

1. Výpočty účinků výbuchu havarijně uniklých plynů/par/prachů

1.1 Fyzikální výbuch

Jako fyzikální výbuch se označuje havarijní únik stlačeného plynu po prasknutí pláště nádoby, nádrže, které může nastat závadou regulátoru tlaku, odlehčovacího ventilu, zeslabením pláště korozí, přehřátím, působením vnějšího plamene nebo mechanického úderu. Obsah nádoby se uvolňuje rázovou vlnou a její úlomky – fragmenty, jsou nasměrovány od místa prasknutí. V literatuře, např. [3], [4] jsou často uváděny následující jednoduché modely pro výpočetní odhady energie výbuchu a výbušného tlaku, např.:

Brodeho/Bakerova metoda odhaduje energii výbuchu podle vzorce (1)

E = (P₁ − P₀) . V / (γ − 1) (1)

kde je

E: energie výbuchu (J),
P₁: počáteční tlak stlačeného plynu (Pa),
P₀: tlak okolní atmosféry (Pa),
γ: poměr tepelných kapacit expandujícího plynu C_p/C_v (bezr.).

Když výbuch nastane na zemi, tak se E odhaduje 2× větší se zohledněním efektu odrazu rázové vlny od podloží.

Prughova metoda počítá energii výbuchu s předpokladem isotermní expanze ideálního plynu podle rovnice (2)

E = (V / V₀) . (P₁ / P₀) . (T₀ / T₁) . R . T₁ . ln(P₁ / P₂) (2)

kde je

E: energie výbuchu (J),
P₀: tlak okolního vzduchu za standartních podmínek (101,3 kPa),
P₁: počáteční tlak expandujícího plynu (Pa),
P₂: konečný tlak expandujícího plynu (Pa),
R: plynová konstanta (8 314 J/(kmol.K),
T₀: teplota okolí za standartních podmínek (273 K),
T₁: počáteční teplota expandujícího plynu (K),
V: objem stlačeného plynu (m³),
V₀: objem 1 mol plynu za standartních podmínek (0,022414 m³).

Průtržný tlak nádoby je odhadován podle rovnice (3), předpokládající rovnoměrné šíření explozivní energie uvnitř kulových nádob.

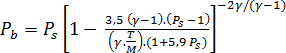(3)

kde je

P_b: průtržný tlak nádoby (bar, abs)
P_s: tlak na povrchu nádoby (bar, abs),
M: molekulová váha expandujícího plynu (kg/kmol),
T: absolutní teplota expandujícího plynu (K),
γ: poměr tepelných kapacit expandujícího plynu C_p/C_v (bezr).

Jsou odhadovány též počáteční rychlosti úlomků nádoby u, viz rovnice (4) a bezpečná vzdálenost doletu těchto úlomků od epicentra výbuchu, r (m) dle rovnice (5), nezahrnující obtékání fragmentů.

u = 3,356 .

(4)

r = 120 .

(5)

kde je

u: počáteční rychlost úlomků (m/s),
P: průtržný tlak nádoby (N/m²),
D: průměr úlomku (m),
m: váha úlomku (kg),
m_TNT: hmotnost TNT (kg),
r: bezp. vzdálenost doletu těchto úlomků od epic. výbuchu (m).

V uvedené literatuře lze nalézt dále experimentálně ověřené výpočetní odhady přetlaku p_t (MPa) na čele vzdušné tlakové vlny pomocí redukované vzdálenosti od epicentra výbuchu podle Sachse R̅ (bezr.) a doby trvání průběhu kladné periody přetlaku t_t (ms) podle následujících rovnic (6), (7) a (8):

Z = r /

nebo

(6)

p_t = 0,1 / R̅ + 0,43 / R̅² + 1,4 / R̅³ (7)

t_t = 1,7.10⁻³ .

(8)

kde je

Z: redukovaná vzdálenost (m/kg^1/3),
R̅: redukovaná vzdálenost podle Sachse (bezr.)
r: vzdálenost terče od epicentra výbuchu (m),
P_a: tlak okolní atmosféry (Pa),
E: energie exploze (J)
t_t: doba trvání průběhu kladné periody přetlaku (ms),
m_TNT: hmotnost TNT (kg).

Rovnice (7) platí pro výbuchy do výšky 20 m. Používané jsou rovněž rovnice výpočtu odhodu výbuchu přetlaku podle Brodeho a Hendrycha [3].

Mezi fyzikální výbuchy patří též tzv. BLEVE (Boiling liquid expanding vapour explosion) [5], [6] nádob/nádrží naplněných pod přetlakem kapalinami nebo zkapalněnými plyny, např. N₂ (l), CO₂ (l), ZZP (I), …, které mají bod varu za atmosférického tlaku hluboko pod teplotou okolní atmosféry. Při havarijním prasknutí nádoby a současném úniku kapaliny do okolí, tato okamžitě začne vařit s prudkým vývinem par. V závislosti na druhu kapaliny, tlacích, teplotách uvnitř nádoby může mít expanze par formu exploze s přetlakem tlakové vzdušné vlny schopné poškodit okolní objekty a osoby, a to nejenom nárazem, ale i toxicitou uniklých par.

1.2 Chemický výbuch – exploze

Chemickým výbuchem je prudká oxidace nebo rozkladná chemická reakce, vyvolávající zvýšení teploty, tlaku nebo obojího současně.

Hořlavé plyny, páry hořlavých kapalin nebo prachy uniklé ze zařízení, potrubí, tlakových lahví, cisteren a nádrží jsou nebezpečné chemickým výbuchem, když se promíchají se vzduchem na koncentrace, které leží mezi jejich dolními a horními mezemi výbušnosti. Podle dosavadních poznatků musí být vznikající oblak dostatečně velký dřív, než dojde k jeho zapálení s prodlením (1–5 min), aby byla vyšší pravděpodobnost vytvoření výbušné směsi v mraku působením turbulence.

Po iniciaci/zapálení se plameny šíří touto směsí s přetlakovou vlnou. Výsledkem je buď deflagrace, nebo detonace [5].

Deflagrace je výbuch šířící se podzvukovou rychlostí.

Detonace je výbuch šířící se nadzvukovou rychlostí a vyznačující se rázovou vlnou.

Parametry pro iniciaci [6]–[13]:

Minimální iniciační energie (MIE): nejnižší nahromaděná elektrická energie v kondenzátoru, která je při vybití právě schopná iniciovat nejsnadněji zápalné směsi při stanovených zkušebních podmínkách,
Minimální teplota vznícení (výbušné atmosféry): teplota vznícení hořlavého plynu nebo páry hořlavé kapaliny nebo minimální teplota vznícení oblaku zvířeného prachu, při stanovených zkušebních podmínkách.

Výbušná směs/atmosféra po iniciaci je charakterizována [7]–[9]:

Maximálním výbuchovým tlakem (p_max): maximální tlak vznikající v uzavřené nádobě při výbuchu výbušné atmosféry za stanovených podmínek zkoušky,
Maximální rychlostí nárůstu výbuchového tlaku ((dp/dt)_max): maximální hodnota nárůstu tlaku za časovou jednotku při výbuchu všech výbušných atmosfér v rozsahu výbušnosti hořlavé látky v uzavřené nádobě za stanovených zkušebních podmínek,
Maximální experimentální bezpečnou spárou (MESG): maximální spára mezi dvěma částmi ve vnitřní komoře zkušebního zařízení, která, je-li plynná směs iniciována za stanovených zkušebních podmínek, zamezí iniciaci vnější plynné směsi 25 mm dlouhou spárou pro všechny koncentrace zkušebního plynu nebo páry ve vzduchu.

Deflagrace bývá pravděpodobnější než detonace. Detonace na otevřeném prostranství je málo pravděpodobná. To závisí též na energii iniciačního zdroje.

Silnější zdroj – vyšší pravděpodobnost detonace. Nehomogenní struktura oblaka plynů/par/prachů volně se rozptylující do atmosféry pravděpodobně brání detonaci.

K detonaci jsou více náchylné hořlavé látky, které mají vyšší rychlost hoření, např. H₂ , C₂H₂ , C₂H₄ atd. a musí jich být dostatečné množství. U vodíku se uvádí např. 30 kg.

Pro deflagraci v uzavřeném objemu, např. nádobě, místnosti, objektu lze aplikovat následující výpočetní odhady maximálního výbuchového tlaku (p_max), energie výbuchu E, ekvivalentního množství TNT (m_TNT), maximální rychlost nárůstu tlaku ((dp/dt)_max), deflagrační konstanty pro plyny (K_g) a pro prachy (K_st) [3], [4]:

a) Výpočet maximálního výbuchového tlaku (p_max)

P_výb = (n_zpl / n_reak) . (T_výb / T_o) . P_a (9)

P_max ≐ (T_ad / T_o) . P_a (10)

kde je

P_výb: výbuchový tlak,
P_max: max. výbuchový tlak, uvolněný při dokonalém spálení hořlavého plynu (kPa),
P_a: počáteční atmosférický tlak (kPa),
T_o: počáteční (okolní) teplota (K),
T_výb: teplota plamene při výbuchu (K),
T_ad: adiabatická teplota plamene (K),
n_zpl: počet molů plynných zplodin generovaných výbuchem (vč. inertu),
n_reak: počáteční počet molů plynu reaktantů (vč. inertu).

V důsledku přítomnosti přibližně 80 % inertů ve vzduchu (N₂, Ar) je uvedený poměr počtu molů roven přibližně jedné, což umožňuje rovnici (9) zjednodušit na rovnici (10). Za optimálních podmínek, kdy je maximální teplota hoření rovná adiabatické teplotě a nedochází ke ztrátám tepla, je výbuchový tlak maximální. Adiabatickou teplotu plamene lze jednoduše vypočítat ze spalného tepla hořlavé látky a molárních tepelných kapacit. Pro praktické výpočty je vhodné mít tyto údaje připravené v tabulce, viz příloha 1.

b) Výpočet energie výbuchu/tlakové vlny (E)

E = α . ΔH_s . m_HP (11)

kde je

E: energie výbuchu (kJ),
α: účinnost výbuchu (podíl energie hoření na tvorbě výbušné vlny (bezr.),
ΔH_s: spalné teplo (kJ/kg),
m_HP: hmotnost uniklých hořlavých plynů/par (výbušné látky) (kg).

c) Výpočet ekvivalentní hmotnosti TNT (m_TNT)

m_TNT = E / 4680 (12)

kde je

E: energie výbuchu (kJ)
E_TNT: 4680 kJ/kg

d) Výpočet maximální rychlosti nárůstu tlaku (dp/dt)_max

(dp/dt)_max = ΔP / Δt = (P_max − P_poč) / (R / v_pl) (13)

kde je

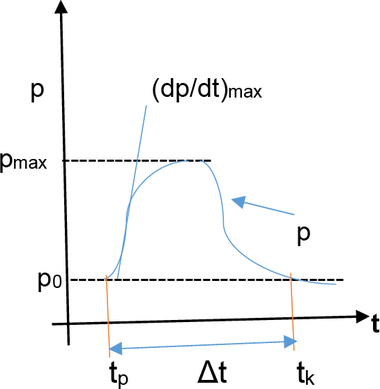
(dp/dt)_max: max. směrnice přímky v grafické závislosti průběhu tlaku na čase, viz obr. 2 (kPa/s),
P_max a P_poč: maximální výbuchový tlak a počáteční tlak okolí (kPa),
Δt: doba trvání výbuchu (ms) v uzavřené nádobě o poloměru R (m) s iniciací ve středu,
v_pl: rychlost plamene (m/s).

e) Výpočet deflagrační konstanty pro plyny a prachy (K_p, K_pr)

K_p , nebo K_pr = V^1/3 . (dp/dt)_max (14)

kde je

V: objem nádoby (m³),
(dp/dt)_max: maximální směrnice přímky v grafické závislosti průběhu tlaku na čase, viz obr. 2 (maxim. rychlost nárůstu tlaku) (Pa/s),
K_p nebo K_pr: též se označuje jako kubická konstanta (Pa.m/s)

Všechny tyto výpočty lze snadno realizovat v excelovských tabulkách s vloženými vzorci a po dosazení příslušných vstupních dat. Autor ověřil aplikaci rovnic (9) až (12) na příkladu havarijního úniku 10 kg acetylénu z plné 50l tlakové láhve při teplotě okolí 25 °C a tlaku 101,35 kPa, viz příloha 1. Výsledky: p_max = 999,76 kPa, E = 482 200 kJ, m_TNT = 107,15 kg. Pro další výpočty jsou v příloze 1 uvedeny hodnoty T_ad (°C) a ΔH_s (kJ/kg) dalších 11 hořlavých plynů.

1.3 Charakteristika účinků výbuchu

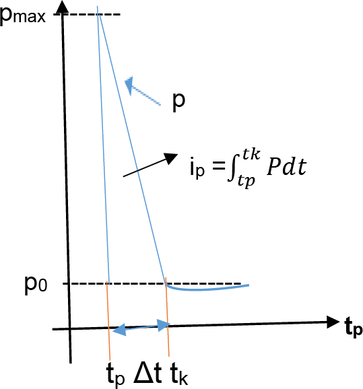
Výbušné zplodiny expandují do okolí vysokými rychlostmi (podzvukovými u deflagrace a nadzvukovými u detonace) a ve vzduchu okolí vytvářejí deflagrační tlakové vlny nebo detonační rázové vlny s rozdíly průběhu jak znázorňují obr. 2 a 3.

Rázové vlny jsou speciální případ tlakových vln. Stejně jako tlakové vlny mají p_max, ale na rozdíl od nich je u nich téměř nekonečně rychlý nárůst tlaku (dp/dt)_max.

Obr. 2 Schéma průběhu tlakové vlny
(dp/dt)_max je konečná

Obr. 3 Schéma průběhu tlakové vlny při deflagraci, při detonaci,
(dp/dt)_max = nadzvuková (→ ∞)

Vysvětlivka ke grafu: i_p = impuls přetlaku jako plocha pod kladným průběhem tlakového pulzu (Pa.s), t_p a t_k = doba počátku a doba trvání kladného tlakového pulzu (ms).

Závěr

Na tento článek navazuje další text s názvem „Empirické modely charakteristik nebezpečí výbuchů a požárů, odhad charakteristik a kategorizace staveb“, který přináší i podrobné závěrečné shrnutí.

Literatura

NEDĚLNÍKOVÁ, H.: Požáry od výbuchů s únikem NCHL v ČR (výtah ze statistiky požárů). Praha: MV – GŘ HZS ČR, 2019.
Statistická ročenka 2019 – Česká republika. Praha: MV – GŘ HZS ČR, 2020.
Guidelines for Chemical Process Quantitative Risk Analysis. N. York, USA CPS – American Institute of Chemical Engineering, 2000.
SFPE Handbook of Fire Protection Engineering.
ČSN ISO 8421-1: 1996. Požární ochrana – Slovník – Část 1: Obecné termíny a jevy požáru.
ČSN EN 1127-1 ED2: 2012. Výbušná prostředí – Zamezení a ochrana proti výbuchu – Část 1: Základní pojmy a metodologie.
ČSN EN 15967: 2012. Stanovení maximálního výbuchového tlaku a maximální rychlosti výbuchového tlaku plynů a par.
ČSN EN 60019-20-1:2010. Výbušné atmosféry – Část 20-1: Materiálové vlastnosti pro klasifikaci plynů a par – Zkušební metody a data.
ČSN EN 14034-1 + A1:2011. Stanovení výbuchových charakteristik rozvířeného prachu – Část 1: Stanovení maximálního výbuchového tlaku pmax rozvířeného prachu.
ČSN EN 14034-2 + A1:2011. Stanovení výbuchových charakteristik rozvířeného prachu – Část 2: Stanovení maximální rychlosti nárůstu výbuchového tlaku (dp/dt)max rozvířeného prachu.
ČSN EN 14034-3 + A1:2011. Stanovení výbuchových charakteristik rozvířeného prachu – Část 3: Stanovení dolní meze výbušnosti rozvířeného prachu.
ČSN EN 14034-4 + A1:2011. Stanovení výbuchových charakteristik rozvířeného prachu – Část 4: Stanovení mezní koncentrace kyslíku LOC rozvířeného prachu.
ČSN EN 1839, ed. 2: 2017. Stanovení mezí výbušnosti a mezní koncentrace kyslíku pro hořlavé plyny a páry.
NFPA 2112: 2018. Standard on Flame Resistant Clothing for Protection of Industrial Personnel Against Short-Duration Thermal Exposure from Fire.
DVOŘÁK, O.: Výpočetní odhady havarijních úniků plynů a kapalin. Praha: TZB-info, 9. 3. 2020.
DVOŘÁK, O.: Trojúhelníkové výbuchové diagramy hořlavých látek a jejich praktická využitelnost. Praha: časopis 112, ročník XVII, č. 3, 2018.
DVOŘÁK, O.: Požární charakteristiky pro pokročilé modelování požárů. Praha: TZB-info, 9. 3. 2020.
AICHE/CCPS: 1994. Guidelines for Evaluation of the Characteristics of Vapour Cloud Explosions, Flash Fire and BLEVES.
A Guidance Manual for Modelling Hypothetical Accidental Release to the Atmosphere. American Petroleum Institute, Washington, 1996.
ČSN EN 1991-1-7:2007. Euro kód 1: Zatížení konstrukcí – Část 1-7: Obecná zatížení – Mimořádná zatížení.
ČSN EN 1991-1-4:2007. Euro kód 1: Zatížení konstrukcí – Část 1-4: Zatížení zásobníků a nádrží. ČNI.
ČERNÍN, M. a kol.: Příručka proti výbuchové ochrany staveb. Nakladatelství ČVUT v Praze, 2008.
DVOŘÁK, O. a kol.: Vývoj a validace požárních modelů pro stanovení vývinu a šíření tepla, kouře, toxických plynů a tlakových vln pro simulace a interpretace scénářů požárů/výbuchů a jejich ničivých účinků. DVZ výzkumného projektu č. VD20062010A07. Praha: MV – GŘ HZS ČR-TÚPO, 2009.

Příloha 1

Příklad aplikace rovnic č. (9–12) z článku
Vstupní data:
Hořlavá látka	`T`_ad °C	Δ`H`_c kJ/kg	`m`_HL kg	`T`₀ K	`P`_a kPa
H₂ – Vodík [g]	2 252	130 800
CO – Oxid uhelnatý	2 387	10 100
CH₄ – Metan	1173	50 030
C₂H₂ – Acetylén	2 637	48 220	10	298	101,3
C₂H₄ – Etylén	2 289	47 170
C₂H₆ – Etan	1 229	47 490
C₃H₆ – Propen	2 232	45 790
C₃H₈ – Propan	1 281	46 360
n-C₄H₁₀ – Butan	1 339	45 720
n-C₇H₁₆ – Heptan	1 419	44 560
n-C₈H₁₈ – Oktan	1 359	44 440
C₆H₆ – Benzen	2 836	40 000
Výsledky výpočtů:
`p`_max	999,76	kPa
`E`	482 200	kJ
`m`_TNT	107,15	kg

English Synopsis

Empirical models of explosion and fire characteristics and their scenarios

The paper summarizes scenarios of accidental leaks of gases and liquids. Their danger is evidenced by the statistics of fires from explosions in the Czech Republic for the period 2012-2019. It also presents empirical models of selected characteristics of physical and chemical explosions of leaked gases and liquids. The paper is supplemented by an example of calculation.