Reklama

Parametrická studie odolnosti dřevobetonových spřažených nosníků

Ing. Jan Břečka, Ing. Kristýna Hrabovská

Recenzovaný

Cílem této studie je nalézt závislosti mezi rozpětím spřaženého dřevobetonového nosníku a dalšími zvolenými parametry spřažených dřevobetonových nosníků. Pro analýzu bylo použito jehličnaté dřevo kategorie C24 a beton třídy C25/30 a C30/37 tloušťky 50 mm. Jako spřahovací prvky byly zvoleny vruty SFS Intec. Pro výpočet byla použita návrhová metoda založená na teorii lineární pružnosti. Poddajnost spřažení byla zohledněna součinitelem poddajnosti γ (γ-metoda).

Reklama

Článek byl vydán v rámci odborné konference doktorského studia Juniorstav 2021.

1. Úvod

Dřevobetonové spřažené konstrukce se používají především pro zesilování stávajících stropů s dřevěnými stropními nosníky. Velkou perspektivu mají v případě dřevobetonových stropů vícepodlažních dřevostaveb. Použitím těchto kompozitních konstrukcí se výrazně zvyšuje tuhost, únosnost, kročejová a vzduchová neprůzvučnost stropní konstrukce a také její požární odolnost. Pokud jsou pro spřažení dřevěných prvků s betonovými prvky použity mechanické spojovací prostředky, je již tato problematika zapracována do skupiny evropských norem ČSN EN. Výpočet provedený dle norem ČSN EN je samozřejmě konzervativní a tuhost spřahovacích prostředků je cca o 20 % nadhodnocována, protože norma předpokládá, že spřahovací prostředek je v betonu dokonale vetknut a při zatížení nedochází k jeho zatlačení do betonu. Pokud se předpokládá, že se spojovací prostředek kolíkového typu ve spoji dřevo-beton s mezivrstvou deformuje, je tento spojovací prvek namáhán také osovou silou, která vzniká od jeho ohybu a ukotvení do dřeva a betonu. Tato osová síla k sobě bude přitlačovat betonovou desku a dřevěný nosník a zvyšuje tak únosnost spojovacího prostředku. Na zvýšení únosnosti spojovacího prostředku se také podílí složka osové síly ve skloněné části spojovacího prostředku, působící rovnoběžně se spárou mezi dřevem a betonem [3],[4].

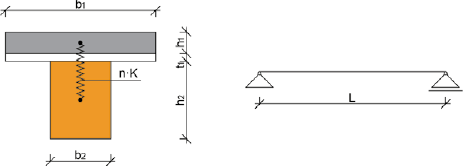
Obr. 1 Geometrie spřaženého dřevobetonového nosníku s proměnnými parametry

Předmětem studie jsou čtyři sady dřevobetonových nosníků, které mají proměnné rozpětí, 2 různé průřezy nosníků a 2 různé třídy betonu. Typ spřahovacích prvků a působící zatížení nejsou měněny. Typický řez dřevobetonovým nosníkem je na obr. 1. Při výpočtu byla respektována veškerá ustanovení uvedená v normě ČSN EN 1995-1-1 v odst. B.2 přílohy B k Eurokódu 5 [1] a veškerá ustanovení uvedená v normě ČSN EN 1992-1-1 [2].

Neměnné parametry: 1) Bednění OSB tl. 18 mm, 2) Spřahovací prvky ASSY plus VG 8×220, 3) Zatížení vl. tíhou, ost. stálé 1 kN/m² a proměnné zatížení 1,5 kN/m².

2. Přehled současného stavu

Trend používání dřeva a betonu pro navrhování kompozitních stavebních prvků lze sledovat jak v mostním tak pozemním stavitelství, které optimálně využívají vlastností dřeva a betonu. Problém při navrhování dřevobetonových konstrukcí je v tom, že neexistují žádná obecně platná pravidla nebo normy pro navrhování (aktuálně platná norma [1] je použitelná pouze pro návrh prostých nosníků z kompozitních materiálů) a současně neexistují metodiky pro výpočet spřažených dřevobetonových nosníků s mezivrstvou např. z OSB desek, které by zohledňovaly reálněji např. tření mezi těmito plochami a přídavné namáhání spřahovacích prvků v této vrstvě.

V rámci mnoha experimentálních prací zabývajících se zkouškami dřevobetonových nosníků je sledováno chování při použití normálního betonu C25/30. Po porovnání s výsledky získanými výpočtem podle Eurokódu 5, je hodnocena možnost použití konstrukčního standardu i pro betony vyšších pevností.

3. Metodika

Obr. 2 Průběh normálových napětí po výšce průřezu [1]

Po zvolení počátečního průřezu dřevěného prvku a tloušťky betonové desky je určena spolupůsobící část betonu dle normy [2]. Zatížení je známo dle projektové dokumentace a požadavků investora a volba spřahovacích prostředků je již na projektantovi. Dřevobetonový spřažený nosník je nutné posoudit na počátku životnosti a na konci životnosti, neboť ve dřevě probíhají časově závislé změny mechanických vlastností. V betonu rovněž probíhají různé reologické procesy. Posudek předpokládá, že normálová napětí mají po výšce striktně lineární charakter, viz obr. 2. Návrhová metoda je tedy založena na teorii lineární pružnosti a na následujících předpokladech:

nosníky jsou prostě podepřeny
jednotlivé části (beton a dřevo) jsou spojeny mechanickými spojovacími prostředky s modulem prokluzu K
rozteč mezi spojovacími prostředky je konstantní nebo se stejnoměrně mění podle posouvající síly
zatížení působí ve směru osy z a vyvozuje moment M = M(x) s průběhem ve tvaru sinusoidy nebo paraboly

Účinná ohybová tuhost je uvažována dle vztahu (1)

(1)

kde E je modul pružnosti v tahu a tlaku betonového nebo dřevěného prvku, I je moment setrvačnosti betonového nebo dřevěného prvku, γ je součinitel poddajnosti, A je průřezová plocha prvku, a je vzdálenost od těžiště celého průřezu do středu dřevěného nebo betonového prvku.

Normálová napětí v betonovém prvku jsou vypočítána dle vztahů (2) a (3). a₁ je vypočítáno dle (4) a označuje vzdálenost mezi těžištěm celého průřezu a středem dřevěného nosníku. h₁ je vypočítáno dle (5) a označuje vzdálenost mezi těžištěm celého průřezu a středem betonového nosníku.

(2)

(3)

(4)

(5)

Napětí v horních vláknech betonu jsou porovnána s návrhovou pevností betonu v tlaku (6).

(6)

Napětí ve spodních vláknech betonu jsou porovnána s návrhovou pevností betonu v tahu (7).

(7)

Normálová napětí v dřevěném prvku jsou vypočítána dle vztahů (8) a (9).

(8)

(9)

Napětí v horních a spodních vláknech dřevěného prvku jsou vyjádřena pomocí vztahů (10) a (11).

(10)

(11)

Následně je vypočítána návrhová pevnost dřevěného prvku v ohybu a návrhová pevnost dřevěného prvku v tahu dle vztahů (12) a (13).

(12)

(13)

A toto kombinované namáhání je posouzeno s limitními požadavky dle vztahu (14).

(14)

Při návrhu spřaženého dřevobetonového nosníku musí být posouzena smyková únosnost dřeva dle vztahu (15).

(15)

Zatížení na spojovací prostředky mezi betonovou deskou a dřevěným nosníkem je vypočítáno dle vztahu (16),

(16)

kde s₁ je osová vzdálenost mezi spojovacími prostředky a n_ef je efektivní počet spřahovacích prostředků v řadě.

Procedurou uvedenou výše je vyšetřen mezní stav únosnosti (MSÚ) spřažených dřevobetonových nosníků na počátku životnosti. Obdobným způsobem se vyšetří MSÚ spřažených dřevobetonových nosníků na konci životnosti. Jediným rozdílem v těchto výpočtech je, že se uvažují rozdílné moduly pružnosti v tahu a tlaku E obou materiálů (je uvažováno s reologickými vlastnostmi obou materiálů) a rozdílné moduly prokluzu spřahovacích prostředků.

V posledním kroku je potřeba vyšetřit limitní průhyby spřažených dřevobetonových konstrukcí, čili posoudit mezní stav použitelnosti (MSP).

MSP na konci životnosti je vypočítán ve dvou krocích. V prvním kroku je vypočítán průhyb od stálých zatížení a kvazistálé složky proměnného zatížení dle vztahu (17)

(17)

kde g_0,_k je vlastní tíha spřaženého nosníku, g_1,_k je ostatní stálé zatížení a ψ₂q_k je kvazistálá složka proměnného zatížení.

Od tohoto zatížení je vypočítán průhyb nosníku dle vztahu (18)

(18)

Ve druhém kroku je vypočítán průhyb od zbylého kvazistálého proměnného zatížení, viz vztahy (19) a (20).

(19)

(20)

Celkový průhyb nosníku dostaneme sečtením výše uvedených průhybů (21).

(21)

Tab. 1 První sada nosníků (nosník 140×180 – C24, beton C25/30, osová vzdálenost 0,8 m)
Počátek životnosti						Konec životnosti
`L` [m]	`σ_ct` / `σ_cd`	`σ_c,b` / `f_ctd`	`τ_2,max` / `f_v,d`	`F₁` / `F_R,d`	`w` / `w_lim`	`σ_ct` / `σ_cd`	`σ_c,b` / `f_ctd`	`τ_2,max` / `f_v,d`	`F₁` / `F_R,d`	`w` / `w_lim`
2,4	0,12	1,49	0,09	0,57	0,10	0,08	0,87	0,09	0,62	0,13
2,8	0,16	1,94	0,10	0,87	0,15	0,11	1,11	0,11	0,94	0,19
3,2	0,18	1,68	0,11	0,85	0,16	0,12	0,84	0,12	0,90	0,21
3,6	0,20	1,43	0,12	0,81	0,18	0,14	0,59	0,13	0,84	0,23
4,0	0,23	1,53	0,14	0,96	0,23	0,16	0,57	0,14	0,99	0,30

Tab. 2 Druhá sada nosníků (nosník 140×180 – C24, beton C30/37, osová vzdálenost 0,8 m)
Počátek životnosti						Konec životnosti
`L` [m]	`σ_ct` / `σ_cd`	`σ_c,b` / `f_ctd`	`τ_2,max` / `f_v,d`	`F₁` / `F_R,d`	`w` / `w_lim`	`σ_ct` / `σ_cd`	`σ_c,b` / `f_ctd`	`τ_2,max` / `f_v,d`	`F₁` / `F_R,d`	`w` / `w_lim`
2,4	0,11	1,44	0,09	0,59	0,10	0,07	0,84	0,10	0,65	0,13
2,8	0,14	1,80	0,10	0,86	0,15	0,09	1,03	0,11	0,93	0,19
3,2	0,15	1,57	0,11	0,85	0,16	0,10	0,79	0,12	0,90	0,21
3,6	0,17	1,34	0,12	0,81	0,18	0,12	0,57	0,13	0,84	0,23
4,0	0,20	1,43	0,14	0,96	0,23	0,14	0,55	0,14	0,99	0,30

Tab. 3 Třetí sada nosníků (nosník 200×200 – C24, beton C25/30, osová vzdálenost 1,5 m)
Počátek životnosti						Konec životnosti
`L` [m]	`σ_ct` / `σ_cd`	`σ_c,b` / `f_ctd`	`τ_2,max` / `f_v,d`	`F₁` / `F_R,d`	`w` / `w_lim`	`σ_ct` / `σ_cd`	`σ_c,b` / `f_ctd`	`τ_2,max` / `f_v,d`	`F₁` / `F_R,d`	`w` / `w_lim`
4,4	0,23	1,11	0,16	0,96	0,24	0,17	0,25	0,17	0,98	0,30
4,8	0,26	1,09	0,19	0,98	0,29	0,20	0,15	0,19	0,99	0,37
5,2	0,30	1,05	0,22	0,94	0,36	0,23	0,02	0,22	0,95	0,46
5,6	0,35	1,05	0,25	0,95	0,43	0,27	0,09	0,25	0,96	0,56
6,0	0,38	0,91	0,27	0,82	0,51	0,30	0,29	0,27	0,82	0,66

Tab. 4 Čtvrtá sada nosníků (nosník 200×200 – C24, beton C30/37, osová vzdálenost 1,5 m)
Počátek životnosti						Konec životnosti
`L` [m]	`σ_ct` / `σ_cd`	`σ_c,b` / `f_ctd`	`τ_2,max` / `f_v,d`	`F₁` / `F_R,d`	`w` / `w_lim`	`σ_ct` / `σ_cd`	`σ_c,b` / `f_ctd`	`τ_2,max` / `f_v,d`	`F₁` / `F_R,d`	`w` / `w_lim`
4,4	0,19	1,01	0,16	0,95	0,23	0,14	0,23	0,17	0,96	0,30
4,8	0,22	1,01	0,19	0,98	0,29	0,17	0,14	0,19	0,99	0,37
5,2	0,26	0,99	0,22	0,95	0,35	0,19	0,04	0,22	0,96	0,46
5,6	0,29	0,99	0,25	0,91	0,43	0,22	0,06	0,25	0,92	0,56
6,0	0,33	0,96	0,27	0,90	0,51	0,25	0,18	0,27	0,91	0,66

4. Závěr

Byla provedena studie odolnosti spřažených dřevobetonových nosníků pro rozpětí 2,4–6,0 m. Byl sledován vliv třídy betonu na mezní stav únosnosti (MSÚ) a mezní stav použitelnosti (MSP) těchto sad nosníků. Ve všech sadách byla použita betonová deska tloušťky 50 mm, byly rovněž použity spřahovací vruty ASSY plus VG 8×220 a bylo aplikováno stejné zatížení. Stálé zatížení bylo uvažováno hodnotou 1 kN/m² a užitné hodnotou 1,5 kN/m² (jako pro obytné místnosti). Všechny sady byly optimalizovány vždy na maximální využití spřahovacích prostředků. Jako impuls pro využití dřevobetonových nosníků, kdy má jejich použití již význam, byla vnímána deformace na konci životnosti větší než 50 % limitní hodnoty. Do této hodnoty má význam použití nespřažených konstrukcí, pokud není potřeba užít betonových desek ke zvýšení požární odolnosti konstrukce.

V rámci parametrické studie bylo zjištěno, že třída betonu výrazně neovlivňuje pevnost spřažené dřevobetonové konstrukce. Tahová napětí v betonu musí být v každém případě zachycena betonářskou výztuží (KARI sítěmi). Osové vzdálenosti spřažených nosníků je možné volit, při působení běžných zatížení, větší než 1,5 m. Spřažené dřevobetonové nosníky je vhodné navrhovat, při běžných zatíženích, od rozpětí 5,5 m a více.

Poděkování

Příspěvek byl vypracován v rámci řešení úloh začleněných do projektu specifického vysokoškolského výzkumu GA VUT č. FAST-J-20-6375.

Literatura

ČSN EN 1995-1-1 Navrhování dřevěných konstrukcí. Část 1.1: Obecná pravidla – Společná pravidla a pravidla pro pozemní stavby. Praha: ČAS, 2006.
ČSN EN 1992-1-1 ed. 2 Navrhování betonových konstrukcí. Část 1.1: Obecná pravidla a pravidla pro pozemní stavby. Praha: ČAS, 2019.
DIAS, A., SCHÄNZLIN, J., DIETSCH, P. Design of timber-concrete composite structures. Germany: Shaker Verlag GmbH, Aachen, 2018, 228 s.
FELIPI, P., DAMASCENO, F., EMERSON, F. Analysis of the machanical behavior of timber-concrete composite beams through FEM model. Brasil: Av. Trabalhador Sao-Carlense, Sao Paulo, 2017, 16 s.

English Synopsis

Parametrical Study of Timber-concrete Composite Beams Resistance

The aim of this study is to find the dependence between the span and cross section area and other choose parameters of the timber-concrete composite beams. For analysis, we used coniferous wood C24 category and concrete C25/30 and C30/37 class with 50 mm thickness. We set the SFS Intec coupling elements. For calculation was used linear elasticity design method. Pliability of composite was take into account per γ-coefficient (γ-method).