Základy fúzní energetiky II. – Základní fyzika fúzních reaktorů
Jaderná fúze je zdrojem energie Slunce a všech ostatních hvězd. Blíží se ale doba, kdy budeme jadernou fúzí vyrábět elektřinu. Pětidílný seriál Základy fúzní energetiky popisuje současný stav vývoje fúzní elektrárny. Druhý článek se věnuje fyzice fúzních reaktorů. Fúzní elektrárny představují zcela novou technologii, významně odlišnou od stávajících energetických zdrojů včetně jaderných elektráren. Pro energetické využití jaderné fúze musí být splněna Lawsonova kritéria popisující energetické rovnováhy plazmatu a elektrárny. Vlastní fúzní reaktor je popsán řadou specifických geometrických a fyzikálních charakteristik, důležitých pro energetické využití reaktoru.
1. díl seriálu o jaderné fúzi na téma "historie jaderné fúze" naleznete ZDE
Fyzika jaderné fúze
Energetické využití jaderné fúze je založeno na fyzikálním jevu, že při slučování atomových jader lehčích než železo na těžší jádra dochází k uvolnění potenciálu jaderné vazebné energie a vzniklé jádro je lehčí než prostý součet hmotností sloučených jader. Rozdíl hmotností mezi slučovanými jádry a vzniklým jádrem je uvolněn jako volná energie v souladu se vztahem A. Einsteina E = mc2. Nejvíce energie se uvolňuje při slučování jader izotopů nejlehčího chemického prvku vodíku. Chemický prvek vodík má tři izotopy: izotop s jádrem tvořeným jediným protonem označovaný jako vodík (H), izotop s jádrem tvořeným protonem a neutronem označovaný jako deuterium (D) a izotop s jádrem tvořeným protonem a dvěma neutrony označovaným jako tritium (T). Izotopy vodík a deuterium jsou přírodní látky, které se na Zemi hojně vyskytují ve formě sloučenin. Nejvíce vodíku a deuteria se nachází ve světových oceánech jako součást vody, resp. v případě deuteria těžké vody. V průměru na 6 240 atomů vodíku připadá 1 atom deuteria. Tritium vzniká přirozeně nejčastěji vlivem ionizujícího kosmického záření ve vrchních vrstvách zemské atmosféry a uměle v jaderných reaktorech. Na Zemi se ale prakticky nevyskytuje, protože není stabilní a β-rozpadem s poločasem rozpadu 12,3 let se mění na izotop helia 3He.
Aby fúzní reakce proběhla, musí mít jádra dostatečnou energii na překonání elektrostatické coulombovské bariéry. Podle současných poznatků je možné jako zdroj energie použít pouze termojadernou fúzi, při které je atomovým jádrům dodána potřebná energie formou tepla. Jiné mechanismy vyvolání jaderné fúze, například srážky urychlených jader nebo mionová katalýza, spotřebují více energie, než kolik se při následné reakci uvolní.
Fúzní reakce
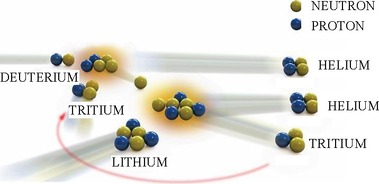
Obr. 10. První generace fúzních energetických reaktorů bude jako palivo používat deuterium a lithium. Odpadem bude inertní plyn helium.
V energetických fúzních reaktorech první generace bude probíhat termojaderná fúzní reakce jader deuteria a tritia (DT reakce), která je nejreaktivnější a umožňuje nejsnáze ze všech fúzních reakcí dosáhnout energetický zisk. Optimální teplota pro reakci deuteria a tritia je při magnetickém udržení přibližně 160 milionů K. Tritium se bude vyrábět přímo v reaktoru reakcí lithia a neutronů vznikajících při fúzní reakci. Celkový proces lze zjednodušeně zapsat jako reakci jader deuteria a lithia za vzniku dvou jader helia a uvolnění 22,4 MeV energie. Jde o složenou reakci, deuterium a lithium mohou reagovat i přímo, avšak za mnohem náročnějších podmínek.
Jaderná reakce I. generace fúzních energetických reaktorů je následující:
Druhá generace fúzních reaktorů bude využívat slučování samotných jader deuteria a lithium již nebude nutné. Většina existujících fúzních zařízení pracuje s fúzní reakcí jader deuteria, avšak dosažení kladného energetického zisku s touto reakci je obtížnější než v případě reakce deuteria a tritia. Reakční proces lze zapsat jako reakci šesti jader deuteria za vzniku dvou jader helia, dvou protonů, dvou neutronů a uvolnění 43,2 MeV energie.
Jaderná reakce II. generace reaktorů je za předpokladu úplné recyklace reaktantů následující:
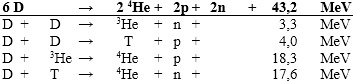
V dalších generacích fúzních reaktorů bude využívána tzv. bezneutronová fúze, například fúzní reakce jader vodíku a bóru, při které vznikají pouze elektricky nabité částice udržitelné magnetickým polem reaktoru. Bezneutronová fúze minimalizuje aktivaci konstrukce reaktoru a otevře cestu pro přímé magnetohydrodynamické generování elektrické energie bez použití termodynamického cyklu.
Lawsonovo kritérium
Jednou z prvních důležitých publikací týkajících se energetického využití jaderné fúze byla práce J. D. Lawsona z roku 1955 [1], ve které byla zformulována podmínka pro energetické využití jaderné fúze, tzv. Lawsonovo kritérium. Lawsonovo kritérium obecně označuje rovnice energetické rovnováhy a stanovuje podmínky pro fúzní reaktor, které musí být splněny, aby byla příslušná energetická rovnováha dosažena.
Dosažení rovnováhy fúzního výkonu a výkonu ohřevu plazmatu se označuje jako vědecký zlom (scientific breakeven), dosažení rovnováhy fúzního výkonu absorbovaného v plazmatu a ztrátového výkonu plazmatu se označuje jako zapálení (ignition). Dosažení rovnováhy výkonu fúzní elektrárny a vlastní spotřeby elektrárny se označuje jako inženýrský zlom (engineering breakeven) [2].
Lawsonovo kritérium stanoví jako podmínku dosažení každé uvedené energetické rovnováhy minimální hodnotu součinu hustoty slučovaných atomových jader n za teploty T a časového intervalu τE, po který budou tyto parametry plazmatu udrženy:
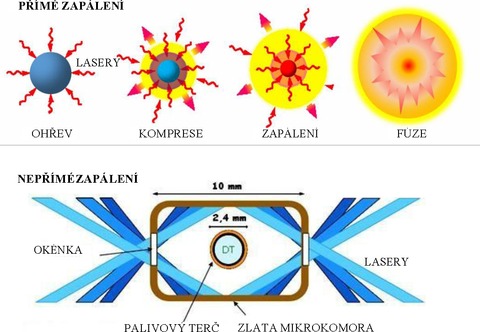
Obr. 11. Inerciální udržení. Při přímém zapálení jsou lasery zaměřeny přímo na palivový terč, v případě nepřímého zapálení do mikrokomory, ve které je terč stlačen vzniklým rentgenovým zářením. Nepřímé zapálení umožňuje dosáhnout rovnoměrnějšího stlačení paliva.
Vzhledem k součinu hustoty a časového intervalu je možné podmínku splnit dvěma různými způsoby: udržet velmi vysokou hustotu jader po velmi krátkou dobu nebo nízkou hustotu jader udržet po delší dobu. První způsob se označuje jako inerciální udržení a předpokládá dostatečně intenzivní stlačení fúzního paliva laserovými nebo rentgenovými paprsky. Druhý způsob označovaný jako magnetické udržení spočívá ve stabilním spoutání fúzního paliva o vysoké teplotě magnetickým polem [3, 4].
Inerciální udržení bylo využito ve vodíkových bombách, avšak pro energetické využití není z celé řady důvodů připravené. Vodíkové bomby využívají pro zapálení fúzní náplně štěpnou jadernou roznětku, kterou ale nelze z fyzikálních důvodů vyrobit dostatečně malou, aby mohla být použita ve fúzním reaktoru. Proto se palivo stlačuje energetickými svazky, obvykle lasery (obr. 11), avšak dosažení potřebné hustoty paliva brání nestability stlačovaného terče. Realizaci energetického reaktoru také brání velmi nízká dosahovaná energetická účinnost a nízký součin výkonu a repetice výstřelů laserů.
Závažným problémem inerciálního udržení je i extrémní zatížení vnitroreaktorových komponent, které by bylo výrazně vyšší ve srovnání s magnetickým udržením. Při mikroexplozích stlačeného paliva bude přibližně třetina fúzního výkonu přenášena ionty a intenzivním rentgenovým zářením, zatímco při magnetickém udržení jsou ionty spoutány magnetickým polem a rentgenové záření vzniká pouze výjimečně.
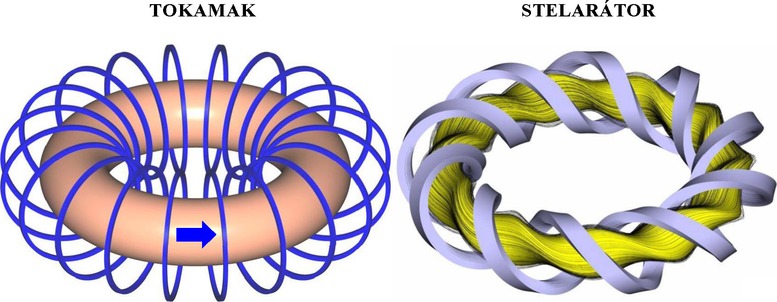
Obr. 12. Magnetické udržení plazmatu v zařízeních tokamak a stelarátor. Modré kruhy a šedá páska znázorňují magnetické cívky. Modrá šipka znázorňuje indukovaný proud v plazmatu. Výhodou stelarátorů je, že nevyužívají elektromagnetickou indukci pro generování elektrického proudu v plazmatu a nativně pracují v kontinuálním režimu; ze stejného důvodu však nedosahují parametrů plazmatu tokamaků.
Magnetické udržení vychází ze skutečnosti, že se při termojaderných teplotách (stovky milionů K) každá látka nachází ve skupenství plně ionizovaného plazmatu. Na ionty a elektrony je možné působit magnetickým polem a takto spoutat látku na teoreticky neomezenou dobu (obr. 12). Vzhledem k velkému pokroku ve vývoji těchto zařízení bude první generace fúzních elektráren postavena na bázi magnetického udržení. Aktuálně budovaný reaktor ITER je také založen na magnetickém udržení a měl by desetinásobně překročit Lawsonovo kritérium vědecké rovnováhy.
Aby bylo plazma při magnetickém udržení stabilně spoutáno, hydrodynamický tlak plazmatu musí být mnohem nižší než tlak udržujícího magnetického pole. Tlak magnetického pole je přitom dán konstrukcí reaktoru a pro daný reaktor je konstantní. Tím je limitován i přípustný hydrodynamický tlak plazmatu p𝑚𝑎𝑥 = 𝑐𝑜𝑛𝑠𝑡. Tlak vodíkového plazmatu v jednotkovém objemu je podle stavové rovnice ideálního plynu rovný součinu hustoty, teploty plazmatu a Boltzmannovy konstanty p = nkT, a proto při dosažení maximálního přípustného tlaku musí hustota plazmatu odpovídat převrácené hodnotě jeho teploty n𝑚𝑎𝑥 ∝ 1/T.
Díky této závislosti analýza obecné nerovnice Lawsonova kritéria neposkytuje pro reaktory s magnetickým udržením prakticky použitelné výsledky a nerovnice musí být upravena do tvaru, který charakterizuje maximální tlak plazmatu dosažitelný při stabilním magnetickém udržení p𝑚𝑎𝑥 = (nT)𝑚𝑎𝑥 = 𝑐𝑜𝑛𝑠𝑡:
Tento zápis Lawsonova kritéria se označuje jako fúzní nebo trojný součin a umožňuje stanovit požadavky pro dosažení energetické rovnováhy v reaktorech s magnetickým udržením. Jak ukazuje obr. 13, v případě reakce DT lze nejsnáze dosáhnout splnění kritérií při optimální teplotě přibližně 160 mil. K, v energetickém vyjádření 14,07 keV. Pro úzký rozsah teplot v okolí optimální teploty se trojný součin zpravidla považuje za konstantní:
Kritérium zapálenín T τE ≥ 5,554 × 1021 [m−3keV s]
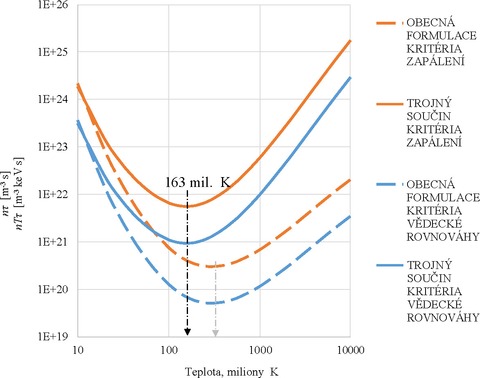
Obr. 13. Graf Lawsonových kritérií pro reakci DT ukazuje optimální teplotu termojaderné fúze v reaktorech s magnetickým udržením 163 mil. K.
Tokamak
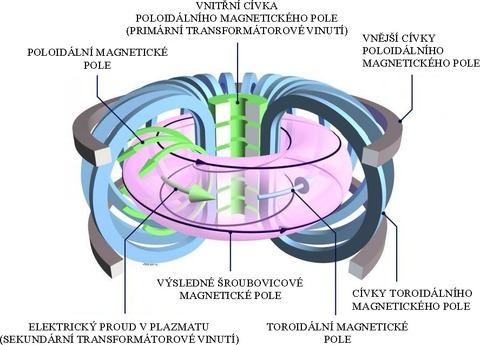
Obr. 14. Základní schéma reaktoru typu Tokamak. Vakuová komora je umístěna na jádru vzduchového transformátoru a je ovinuta magnetickými cívkami. Indukovaný proud v plazmatu a magnetické cívky společně vytvářejí šroubovicové magnetické pole.
Nejpokročilejším fúzním reaktorem je tzv. tokamak [5, 6]. Tokamak je původně ruský koncept charakteristický indukčně generovaným elektrickým proudem v plazmatu, který spoluvytváří magnetické pole a ohřívá plazma.
Hlavní součástí tokamaku je prstencová vakuová komora, umístěná na transformátorovém jádru. Současné tokamaky používají vzduchové transformátory s centrálním solenoidem. Transformátor indukuje v plazmatu uvnitř komory vysoký elektrický proud, který generuje poloidální magnetické pole. Okolo vakuové komory jsou navinuty magnetické cívky, které vytvářejí toroidální magnetické pole. Součtem obou polí vzniká šroubovicové magnetické pole, které spoutává plazma. Indukovaný proud současně plazma ohřívá (obr. 14).
Indukce elektrického proudu v plazmatu je klíčovou předností tokamaků, avšak komplikuje jejich energetické využití. Indukce probíhá pouze při změně elektrického proudu v primárním vinutí transformátoru, a proto tokamaky ze své podstaty pracují v pulzním režimu. Protože výroba elektřiny pro rozvodnou síť vyžaduje konstantní tok energie, musí být fúzní energetický reaktor na bázi tokamaku vybaven zařízením pro neinduktivní generování elektrického proudu. Podle současné koncepce budou fúzní energetické reaktory generovat elektrický proud v plazmatu neinduktivně prostřednictvím vlečných systémů (Current Drive), jako jsou svazky neutrálních atomů a radiofrekvenční vlny, a tzv. bootstrap proudu, který v plazmatu vzniká samovolně v důsledku gradientu tlaku směrem do středu komory. Díky neinduktivní generaci elektrického proudu bude výkon fúzního energetického reaktoru konstantní.
Geometrické charakteristiky reaktoru
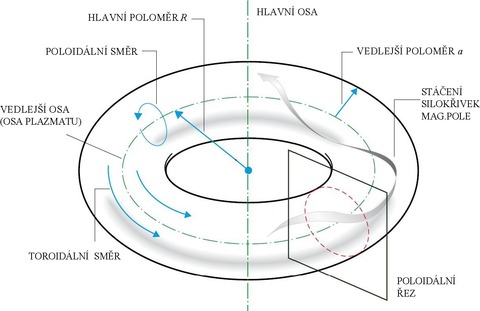
Vakuová komora tokamaku má tvar toroidu s následujícími geometrickými charakteristikami zobrazenými na obr. 15 a 16:
- hlavní poloměr označený R,
- vedlejší poloměr označený a v případě kulatého průřezu, nebo poloosy a a b v případě průřezu ve tvaru D,
- podíl poloos tzv. elongace κx = b ⁄ a,
- toroidální směr,
- poloidální směr,
- vedlejší osa komory v toroidálním směru, osa plazmatu,
- magnetická osa,
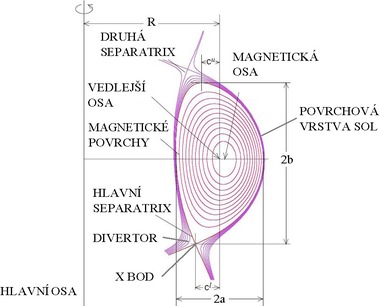
- poslední uzavřený magnetický povrch, tzv. separatrix,
- povrchová vrstva plazmatu SOL (Scrape-off layer), která se nachází vně separatrix.
Na obr. 15 jsou zobrazeny geometrické charakteristiky vakuové komory s kruhovým průřezem. Pro tokamaky je ale vhodnější vakuová komora ve tvaru D (obr. 16). Plazma ve tvaru D má vyšší stabilitu a lepší udržení energie. Současně jsou lépe rozloženy síly působící na magnetické cívky a do komory lze snadněji instalovat divertor pro čištění a tvarování plazmatu.
Vybrané fyzikální charakteristiky reaktoru
Na nabité částice působí v magnetickém poli síla F, kolmá na magnetické siločáry a současně na vektor rychlosti částice. Tato síla je oběma veličinám přímo úměrná. Čím silnější je magnetické pole a čím větší je rychlost částice, tím větší je působící síla. V homogenním magnetickém poli je výsledkem pohyb částice po kružnici. Tento základní krouživý pohyb se nazývá gyrace nebo Larmorova rotace. Poloměr kružnice se označuje jako Larmorův poloměr ρL:
kde m a ec jsou hmotnost a náboj částice, 𝑣⊥ je složka rychlosti částice kolmá k vektoru magnetické indukce B. Ionty a elektrony se pohybují toroidální komorou gyrací podél toroidálních magnetických silokřivek. V toroidální komoře ale není toroidální magnetické pole homogenní a je nepřímo úměrné hlavnímu poloměru komory R. Působením gradientu magnetického pole se částice mohou pohybovat také po tzv. banánové trajektorii (obr. 17).
Faktor β je důležitým parametrem reaktoru, který udává poměr tlaku plazmatu k tlaku magnetického pole. Tlak plazmatu v jednotkovém objemu lze vyjádřit ze stavové rovnice ideálního plynu:
kde n je hustota částic, k je Boltzmanova konstanta a T je teplota částic. Tlak magnetického pole je dán druhou mocninou magnetické indukce B dělené dvojnásobkem permeability vakua μ0:
Po dosazení získáme vztah pro faktor β:
S nárůstem tlaku plazmatu stoupá generovaný fúzní výkon, avšak pro stabilní plazma je nutné udržovat výrazně vyšší magnetický tlak než je tlak plazmatu, tj. β << 1. Parametr β se proto v současných tokamacích pohybuje na úrovni jednotek procent.
Namísto faktoru β se často používá normalizovaný faktor βN, také označovaný jako Troyon faktor:
kde a je malý poloměr plazmatu a I je proud procházející plazmatem.
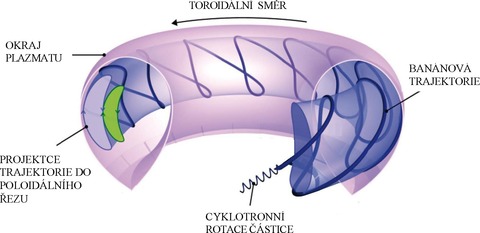
Obr. 17. Banánová trajektorie nabitých částic v toroidálním magnetickém poli tokamaku. Stoupání v toroidálním směru je pro názornost zveličeno, skutečná helicita pole je mnohem pozvolnější. Vyznačena je precese trajektorie v toroidálním směru v důsledku nárůstu helicity směrem do plazmatu (pro názornost je také zveličena) a v levé části možnost výrazného posunu trajektorie v důsledku čelní srážky (zde směrem do středu plazmatu) na zelenou trajektorii.
Greenwaldův limit hustoty označuje empiricky zjištěnou limitní hustotu plazmatu, při jejímž překročení zpravidla dojde ke zhroucení plazmatu:
Bezpečnostní faktor q označuje míru šroubovitosti (helicity) magnetických siločar v toroidální komoře a je roven počtu oběhů nabité částice kolem komory v toroidálním směru, který je nutný k vykonání jednoho oběhu v poloidálním směru.
Vyšší elektrický proud v plazmatu vytváří vyšší poloidální magnetické pole BP. Pokud při růstu proudu zůstává toroidální pole BT nezměněné, mění se šroubovitost výsledného pole a klesá stabilita plazmatu. Hodnota faktoru q v centru plazmatu musí být proto větší než jedna q > 1 a na okraji plazmatu větší než cca 3 qa > 3. Podmínka na okraji plazmatu limituje proud plazmatem podle přibližného vztahu:
Faktor q95 označuje bezpečnostní faktor q pro povrch zahrnující 95 % poloidálního magnetického toku. Faktor se používá pro divertorované plazma, u kterého se v blízkém okolí X-bodu (obr. 16) hodnota faktoru q blíží k nekonečnu q → ∞.
Doba udržení τE je charakteristická doba ztráty energie z fúzního plazmatu. Při tepelné rovnováze je doba udržení energie v plazmatu definována jako poměr celkového obsahu tepelné energie v plazmatu WP k celkovému ztrátovému výkonu PL :
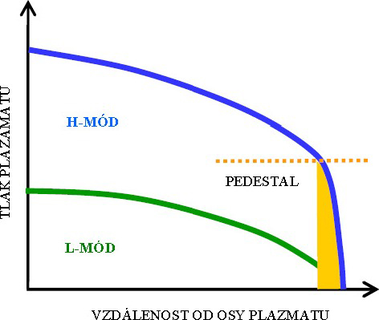
L-mód (Low) a H-mód (High) označují dva stavy plazmatu, odlišující se dobou udržení energie τE. Obvyklý startovací režim reaktoru probíhá v L-módu, režimu s nízkým udržením energie. Za určitých fyzikálních okolností se v povrchové vrstvě plazmatu vytvoří transportní bariéra, která vyvolá strmý nárůst tlaku plazmatu, a dojde ke skokovému zvýšení doby udržení energie. Tento stav se označuje jako H-mód (obr. 18).
Fúzní výkon PF udává výkon fúzních reakcí v plazmatu a lze jej vypočítat podle rovnice:
kde n1 a n2 jsou hustoty reagujících částic, 〈σv〉 je průměrná hodnota součinu relativní rychlosti jader v a účinného průřezu reakce σ(v) přes maxwellovské rozdělení rychlostí při teplotě T označovaná jako fúzní reaktivita, V je objem plazmatu a EF je energie uvolněná při jedné fúzní reakci.
Výkon ohřevu plazmatu PH je výkon, který vstupuje z vnějšku do plazmatu a ohřívá je. Ohřev plazmatu je nezbytný do doby dosažení zapálení plazmatu. Zapálení (Ignition) označuje energetickou rovnováhu, při které celkový výkon nabitých částic vznikajících při fúzní reakci a udržených v plazmatu dosáhne hodnoty ztrát plazmatu. Fúzní reakce pak autonomně ohřívá plazma a externí ohřev není nutný.
Faktor zesílení Q udává poměr mezi fúzním výkonem PF a výkonem ohřevu PH :
Pokud fúzní výkon PF dosáhne výkonu ohřevu PH, nastane Q = 1. Tato energetická rovnováha se nazývá vědecké vyrovnání (Scientific Breakeven). Při dalším zvyšování fúzního výkonu stoupá schopnost plazmatu ohřívat sama sebe. V okamžiku dosažení energetické rovnováhy zapálení (Ignition) může být výkon externího ohřevu nulový PH = 0 a nastává Q = ∞. V praxi ale bude plazma ohříváno i po dosažení stavu zapálení při generování elektrického proudu v plazmatu.
Poděkování
Převzaté obrázky a fotografie byly použity s laskavým svolením ITER (www.iter.org), EUROfusion (www.euro-fusion.org) a Fusion for Energy (fusionforenergy.europa.eu).
Poděkování patří Ing. Milanu Řípovi, CSc., a RNDr. Radomíru Pánkovi, Ph.D., za pečlivé přečtení rukopisu a cenné poznámky.
Použitá literatura
- J. D. Lawson, Some criteria for a power producing thermonuclear reactor, Proc. Phys. Soc. B 70, 6 (1957); původně výzkumná zpráva: A.E.R.E. Report GP/R 1807, Harwell, Berks 1955, A.E.R.E. Amplified version, Harvell, Berks 1956.
- S. Entler, Engineering Breakeven, Journal of Fusion Energy, 34 (2015) 513–518.
- G. McCracken, P. Stott, Fúze – energie vesmíru, Mladá Fronta, 2006
- M. Řípa, a kol., Řízená termojaderná syntéza pro každého – 4U, ÚFP AV ČR, Praha 2013, dostupné na
https://www.euro-fusion.org/downloads/ - J. Mlynář, ITER: cesta ke zvládnutí řízené termonukleární fúze, Pokroky matematiky, fyziky a astronomie 49 (2004) 129–150
- J. Mlynář, O symetrii tokamaku, Čs. čas. fyz. 59 (2009) 207–212
Nuclear fusion is the energy source of the Sun and all other stars. Time is coming when nuclear fusion will produce electricity. A five-part series Mastery of sun describes the state of the art of developing a fusion power plant. The second article deals with the basic physics of fusion reactors. Fusion power is a completely new technology, significantly different from other energy sources including nuclear power. For energy use of nuclear fusion, Lawson criteria describing the plasma energy balance and power must be met. A fusion reactor is characterized by some of the specific geometric and physical characteristics that are important for the fusion power reactor.