Stanovení fyzikálně mechanických parametrů zděné konstrukce stěny na základě full scale testu
V příspěvku je popsána metoda stanovení základních charakteristik zdiva v případě, že nelze provést zkoušky podle příslušných zkušebních norem, což je způsobeno v popisovaném případě zejména velikostí zdicích prvků. Byl proveden průzkum konstrukce, odběr vzorků (které nebylo možno odebrat ve velikosti předepsané např. ČSN EN 1052) a byla provedena velkoplošná zatěžovací zkouška v laboratoři postavené stěny. Následně byly charakteristiky zdiva verifikovány jak výsledky velkoplošné zatěžovací zkoušky, tak i numerickou simulací.
1. Úvod
V některých případech se setkáváme s požadavky, které jsou na původně nenosné konstrukce kladeny v důsledku změny užívání či instalace nových technologií.
Tento příspěvek popisuje případ, kdy původně pouze dělící konstrukci, která byla provedena ze sádrových příčkovek PROMONTA vyzděných na sádrovou maltu, bylo nutno – v důsledku změny užívání – posoudit na účinky vnitřního přetlaku/podtlaku v místnosti, který může vzniknout v průběhu hasebního zásahu v rámci jednoho požárního úseku.
Vzhledem k tomu, že se jedná o příčkovky, které se již řadu let nevyrábí, bylo k dispozici pouze pár základních údajů o příčkovkách a bohužel žádné údaje o vlastnostech zdiva.
Dalším problémem, který v souvislosti s předpokládaným posouzením těchto, původně jen dělících, konstrukcí vyvstal, byly skutečnosti způsobené změnou předpisů pro navrhování/posuzování konstrukcí. Bylo nutno postupovat dle norem řady EC.
Pro výpočty a posouzení příček – vzhledem k jejich nové nosné funkci v objektu – bylo nutno stanovit
- charakteristickou pevnost zdiva v tahu za ohybu s rovinou porušení rovnoběžnou s ložnými spárami fxk1 ,
- charakteristickou pevnost zdiva v tahu za ohybu s rovinou porušení kolmo k ložným spárám fxk2 ,
- charakteristickou pevnost zdiva ve smyku fvk ,
- charakteristickou pevnost zdiva v tlaku fk ,
- krátkodobý modul pružnosti zdiva E,
s tím, že zjištěné hodnoty by měly být určeny ve smyslu normy ČSN EN 1996-1-1, Navrhování zděných konstrukcí, článek 3.6.1, 3.6.2, 3.6.4 a 3.7.2.
2. Stručný popis posuzovaných konstrukcí
Sledované příčky PROMONTA tvoří dělící konstrukce mezi hasebními úseky. Příčky jsou vyzděny ze sádrových tvárnic o tloušťce 80 mm, výšce 500 mm a šířce přibližně 667 mm. Příčky byly vyzdívány mezi ocelovými nosníky (o profilu I100 či U200).
Výška příček není konstantní a závisí na provedení stropu (pohybuje se od 3,7 m v místech pod průvlaky do 4,9 m). Spodní část příček zasahuje většinou pod úroveň podlah do hloubky určené jejich skladbou. Prostor mezi horní částí příčky (zhlavím příčky) a stropem je vyplněn maltou, případně v některých místech byl nalezen na styku příčky a stropu polystyren s maltou.
Příčky jsou vyzděny z tvarovek dle obr. 1, na kterém jsou vyznačeny i rozměry zámku.
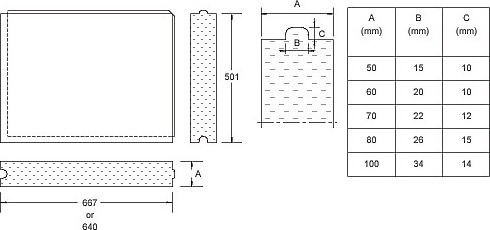
Obr. 1: Sádrová tvárnice PROMONTA
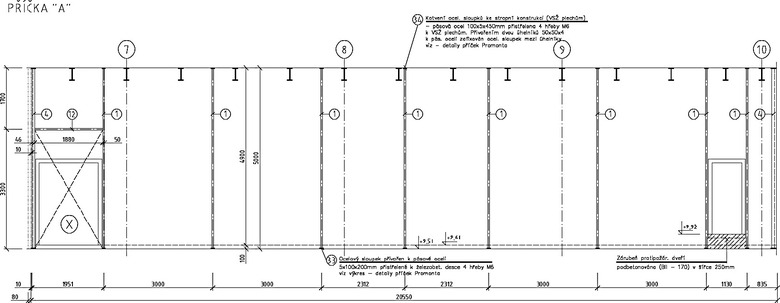
Typické provedení příčky je zřejmé z Obr. 2.
3. Možnosti zjištění fyzikálně mechanických charakteristik
Aby bylo možno výše uvedené fyzikálně mechanické charakteristiky stanovit, bylo nutno uvážit následující skutečnosti, resp. omezení
- zkoušky zdiva dle ČSN EN 1052
- v případě, že by zkoušky měly být plně v souladu s ČSN EN 1052, tak je nutno získat zkušební vzorky (bloky) podle těchto norem tím, že budou vyřezány ze stávající konstrukce.
Normy řady ČSN EN 1052 (zejména ČSN EN 1052-2 a ČSN EN 1052-3) požadují velké zkušební vzorky (větší než 1,5, respektive 3násobek výšky zdicích prvků, navíc kombinaci ložných a styčných spár), což by vyžadovalo vyřezání velmi rozměrných vzorků (odhadem 1,3 × 1,0 m, možná i větší). Objevily se zejména následující komplikace:
- I kdyby se podařilo vzorky vyřezat, tak vzniknou problémy s přepravou vzorků do laboratoře, neboť by s vysokou pravděpodobností mohlo dojít k jejich porušení.
- Bylo by nutno mít minimálně 6 vzorků pro každý typ zkoušky (ohyb v jednom a druhém směru, smyk). Zkoušky tohoto typu vzorků by byly značně finančně náročné, což je zřejmě zcela nereálné i pro finančně silného investora.
- další možností je z konstrukce odebrat tvárnice a vzorky vyzdít v laboratoři. Ale v tomto případě by s vysokou pravděpodobností došlo k porušení tvarovek při odběru a/nebo i při transportu. Proto ani tato možnost nebyla považována za vhodnou.
- v případě, že by zkoušky měly být plně v souladu s ČSN EN 1052, tak je nutno získat zkušební vzorky (bloky) podle těchto norem tím, že budou vyřezány ze stávající konstrukce.
- diagnostický průzkum zdiva a provedení velkoplošné zkoušky vyzděných příček v laboratoři s následným vyhodnocením. Tento postup spočíval v následujících krocích
- diagnostika aktuálního stavu konstrukcí příček spočívá v podrobné prohlídce a zdokumentování stavu příček, především se zaměřením na míru vyplnění ložných a styčných spár maltou a zkouškách menších zkušebních těles.
Předpokládal se odběr jádrových vývrtů a trámečků/hranolů. Odběry vzorků musely být provedeny za sucha (aby se materiál nerozplavil), - vyzdění velkoplošných vzorků (počet by byl stanoven v závislosti na skutečnostech zjištěných v rámci diagnostického průzkumu), jejich zkouška1 a následné vyhodnocení,
- numerické modelování full scale testu,
- stanovení požadovaných charakteristik na základě vyhodnocení prací b1) až b3) a provedení případných dalších studií.
- diagnostika aktuálního stavu konstrukcí příček spočívá v podrobné prohlídce a zdokumentování stavu příček, především se zaměřením na míru vyplnění ložných a styčných spár maltou a zkouškách menších zkušebních těles.
Jak již vyplynulo z předchozího popisu jednotlivých možností, tedy možnosti provedení
- buď zkoušky zdiva dle ČSN EN 1052,
- anebo diagnostického průzkum zdiva, velkoplošné zkoušky vyzděných příček v laboratoři s následným vyhodnocením
plyne, že jedinou vhodnou a ekonomicky přijatelnou metodou pro stanovení charakteristik zdiva je diagnostický průzkum s následnou laboratorní velkorozměrovou zkouškou doplněný o numerické modelování.
Tento přístup byl, po dohodě s objednatelem, zvolen.
4. Diagnostický průzkum zdiva, provedení velkoplošné zkoušky vyzděných příček v laboratoři s následným vyhodnocením
4.1 Diagnostický průzkum zdiva
4.1.1 Průzkum in situ a odběr vzorků pro laboratorní zkoušky
Byla provedena prohlídka stavu konstrukcí, proveden pasport poruch a vytipována místa odběru vzorků. U příček s výškou cca 4,9 m byly vzorky odebírány ze tří výškových úrovní, u nižších příček byly vzorky odebírány pouze ze dvou výškových úrovní.
Při odběru vzorků bylo nutno zohlednit, zda se jedná o vzorek obsahující ložnou (L) či styčnou spáru (S); byly odebírány hranoly o rozměrech 80×160×320 mm (H) a vývrty vnějšího průměru vzorku 95 mm (bez označení) – viz obr. 3. Všechny vzorky byly odebírány zasucha.
4.1.2 Laboratorní zkoušky vzorků
Laboratorní zkoušky na odebraných jádrových vývrtech a trámcích byly prováděny na Ústavu stavebního zkušebnictví fakulty stavební VUT v Brně.
Získané výsledky jsou sumarizovány v tab. 1. Vyčíslena je hodnota sledované veličiny při uvážení všech vzorků, tj. pro všechny vzorky včetně nulových/poškozených a též s jejich vyloučením. Výstupem je ve všech případech střední hodnota veličiny; charakteristická hodnota (5% kvantil) byla stanovena pouze, pokud to počet platných vzorků umožnil. I přes veškerou opatrnost při odběru vzorků, jejich transportu do laboratoře a citlivé zacházení se vzorky před vlastní laboratorní zkouškou nebylo možno některé testy vyhodnotit, neboť naměřené hodnoty se blížily nule.
Na základě provedených laboratorních zkoušek lze konstatovat, že způsob vyplnění spár zdiva příček PROMONTA je velmi různorodý, a to především z hlediska způsobu a kvality provedení ložných (L) i styčných (S) spár. Významně horší – nižší – sledované charakteristiky byly získány pro spáry styčné; viz tab. 1, obr. 4 a 5.
Obr. 4: Příklad vyplnění ložných spár: a) Téměř úplné vyplnění spáry; b) Částečné vyplnění spáry
Obr. 5: Příklad vyplnění styčných spár: a) Téměř úplné vyplnění spár; b) Částečné (velmi špatné) vyplnění spáry
Při interpretaci v tab. 1 uvedených hodnot je však zcela nezbytné uvážit rozdíl normových zkušebních těles a skutečně odebraných a laboratorně testovaných vzorků, které jsou velikostně odlišné (tzv. „diagnostický přístup“).
Aby bylo možno vliv promaltování kvantifikovat, byla provedena zatěžovací zkouška full scale vzorků a rovněž byly výsledky ověřeny numerickým modelováním.
| Řádek číslo | Sledovaná charakteristika (MPa) | Střední hodnoty | Charakteristické hodnoty | ||
|---|---|---|---|---|---|
| Všechny vzorky (i s nulovými hodnotami) | Všechny vzorky (bez nulových hodnot) | Všechny vzorky (i s nulovými hodnotami) | Všechny vzorky (bez nulových hodnot) | ||
| 1 | 2 | 3 | 4 | 5 | |
| 1 | pevnost v příčném tahu fct – vývrty, ložná spára | 0,199 | 0,238 | 0,078 | 0,149 |
| 2 | pevnost v příčném tahu fct – vývrty, styčná spára | 0,061 | 0,139 | 0,007 | 0,055 |
| 3 | pevnost v tahu za ohybu na hranolech fcf – ložná spára | 0,225 | 0,317 | 0,054 | 0,147 |
| 4 | pevnost v tahu za ohybu na hranolech fcf – styčná spára | 0,086 | 0,202 | 0,009 | 0,084 |
| 5 | pevnost ve smyku na vývrtech fs – ložná spára | 0,24 | 0,296 | 0,077 | 0,151 |
| 6 | pevnost ve smyku na vývrtech fs – styčná spára | 0,068 | 0,162 | 0,008 | 0,101 |
| 7 | pevnost ve smyku fs,D (deskový; hranoly z ložné i styčné spáry) | ||||
| 8 | pevnost ve smyku fs,S (stěnový; hranoly z ložné i styčné spáry) | ||||
| 9 | modul pružnosti v ohybu E na hranolech – ložná spára | 2594 | 1373 | ||
| 10 | modul pružnosti v ohybu E na hranolech – styčná spára | 2279 | 1473 | ||
| 11 | Modul v tlaku Ec (materiál tvárnic) | 3261 | 2048 | ||
| 12 | pevnost v tlaku krychelná fc (materiál tvárnic) | 5,423 | 3,909 | ||
| 13 | pevnost malty v tlaku krychelná fm (materiál spár) | 3,598 | 2,246 | ||
4.2 Velkoplošná zkouška vyzděných příček
4.2.1 Příprava velkoplošné zatěžovací zkoušky
Protože se v současné době již tvarovky PROMONTA v ČR nevyrábí, a protože odběrem tvarovek z již provedených konstrukcí by došlo k jejich poškození, bylo nutno hledat podobné tvarovky, ze kterých by mohly být vyzděny zkušební velkoplošné vzorky.
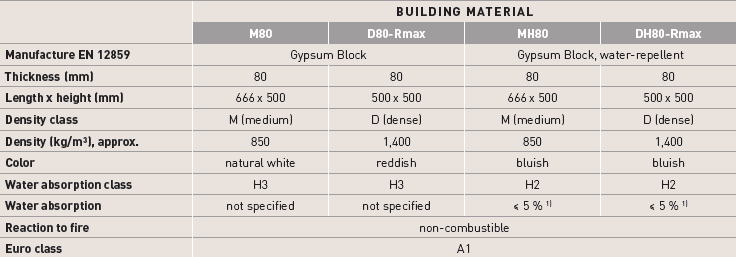
Naštěstí se podařilo nalézt tvarově i fyzikálně mechanickými charakteristikami velmi podobné příčkovky, které jsou vyráběny v zahraničí – viz tab. Tab. 2, příčkovka z materiálu MultiGips M80. Ke tvarovkám je dodáváno i sádrové pojivo MultiGips Fugenfuller; [4], [5].
Tab. 2: Výrobky MULTIGIPS, [4]
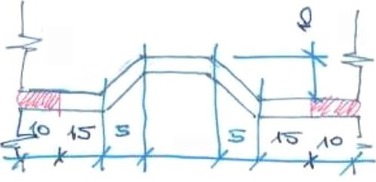
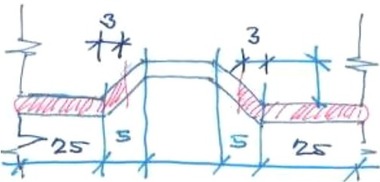
Vzhledem k významně rozdílnému promaltování styčných a ložných spár, které se projevilo jak na odebraných válcích i na hranolech, viz např. obr. 4 a 5, bylo navrženo provést velkoplošný test se dvojím způsobem promaltování
- maximální vyplnění maltových spár,
- minimální vyplnění maltových spár,
a to dle schématu uvedeného na obr. 6.
Aby bylo možno porovnat chování příček z původního materiálu PROMONTA i zkoušených příček z materiálu MULTIGIPS, byly provedeny na zkušebně vyzděné stěně z bloků MULTIGIPS odběry válců pro laboratorní zkoušky a byly provedeny i zkoušky sádrové malty MultiGips Fugenfuller. Bylo prokázáno, že pevnosti vzorků odebraných z příčky z prvků systému MultiGips s minimálním promaltováním spár odpovídají zhruba pevnostem zjištěným na vzorcích odebraných z reálných stěn posuzované konstrukce.
Obr. 6: Podklad pro provedení zkušebních těles z nových tvarovek MULTIGIPS (určeno dle vzorků odebraných ze stávajících příček); a) minimální promaltování, b) maximální promaltování
4.2.2 Konfigurace velkoplošné zatěžovací zkoušky
Zkouška byla provedena na vzorcích realizovaných v měřítku 1:1; šířka odpovídala typickému poli konstrukcí, výška 3,7 m – odpovídá nejnižší výšce příček a velikosti zatěžovacího zařízení.
Schéma zkoušených vzorků je zřejmé z obr. 7. Vzorky se lišily mírou promaltování spár:
- vzorek I: maximální – tj. řádné – promaltování ložných i styčných spár;
- vzorek II: minimální – tj. pouze částečné – promaltování.
Obr. 8: Pohled na zkušební vzorky s osazenou vakuovací membránou: a) zkušební vzorek I, b) zkušební vzorek II
4.2.3 Zkušební postup, sledovaná místa
Zkouška byla provedena vakuováním na svislé vakuovací stolici, která umožňuje vnášet rovnoměrné plošné zatížení podtlakem2. U testovaných vzorků bylo provedeno postupné zatěžování čtyřmi zatěžovacími cykly na hladině 350 Pa (tato byla vždy podržena max. po dobu 5 minut a/nebo do ustálení deformace). Následovalo postupné zvyšování působícího zatížení až do okamžiku kolapsu konstrukce, a to dle navržených a s objednatelem předem odsouhlasených zatěžovacích schémat3; viz obr. 9; skutečně realizovaná zatěžovací schémata se pro vzorek I a II mírně lišila.
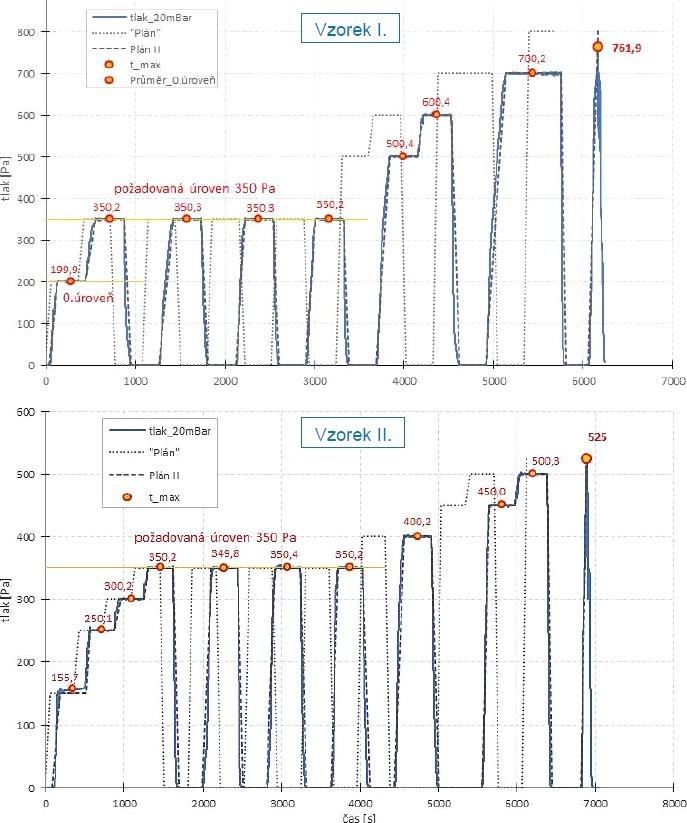
Obr. 9: Závislost působícího tlaku na čase, vzorky I a II
Účinek zatížení na konstrukci byl uvážen jako statický.
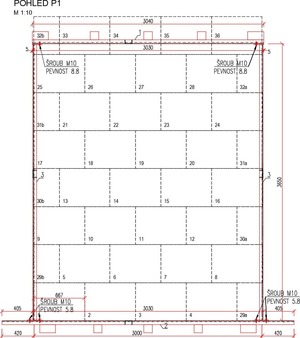
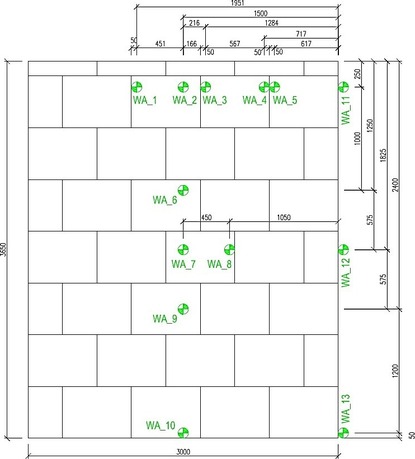
Při zkoušce obou vzorků byl (v závislosti na čase) sledován působící podtlak a především deformace konstrukce kolmo na její střednici, a to v místech dle schématu na obr. 10.
Obr. 10: Poloha bodů měření posunu/deformace příčky a reálné provedení – shodné pro vzorek I i II: a) schéma měřených bodů, b) pohled na stěnu s vyznačenými měřenými body
4.2.4 Výsledky získané ze zatěžovací zkoušky
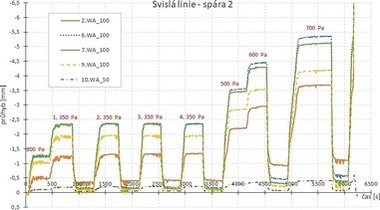
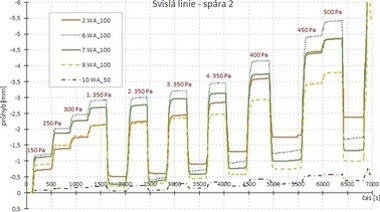
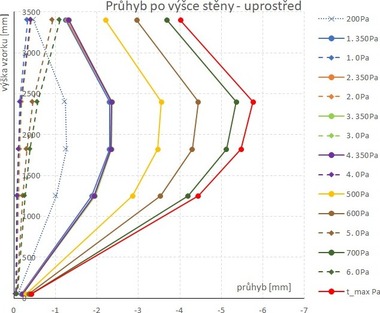
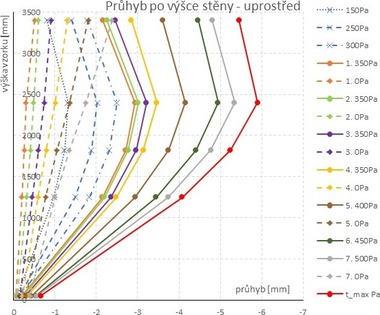
Z důvodů omezeného rozsahu příspěvku jsou uvedeny pouze klíčové výsledky. V průběhu zkoušky byla vždy zaznamenávána závislost deformace kolmo na střednicovou rovinu (vodorovný posun) vzorku na čase a působící hladině přetlaku/podtlaku.
Průběh měřených deformací pro svislou linii snímačů uprostřed vzorku4 je pro vzorek I (vzorek II) zřejmý z obr. 11 a 13, resp. z obr. 12 a 14.
4.2.5 Vzorek I – odezva na vnášené zatížení a způsob porušení
Při cyklování vzorku na 350 Pa nedocházelo ke zvyšování měřené deformace (nejvyšší zaznamenané deformace 2,3–2,4 mm v bodech WA_6 a WA_7 pro všechny cykly) s narůstajícím počtem cyklů. Taktéž zbytkové deformace po odtížení byly velmi nízké (nejvyšší zaznamenány v horní vodorovné linii – do 0,4 mm). Významné zbytkové hodnoty měřených deformací byly zaznamenány až při odtížení vzorku z hladin 600 a 700 Pa, tj. z úrovně zatížení blízko mezní únosnosti vzorku.
Vzorek byl porušen5 při dosažení hladiny působícího podtlaku 761,9 Pa. Této hladině odpovídala maximální zaznamenaná deformace konstrukce cca 5,8 mm (bod WA_6).
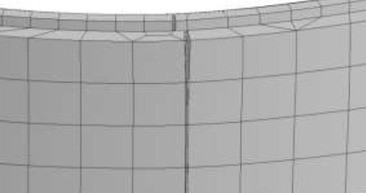
K porušení došlo křehce v oblasti největšího sledovaného průhybu. První trhliny byly pozorovány v dolních rozích vzorku. Ve zhlaví stěny téměř souběžně došlo ke ztrátě celistvosti a zborcení střední části stěny v rozsahu tří řad tvarovek. Dvojice svislých hlavních trhlin procházela svisle dolů přes styčnou spáru i navazující tvarovky zdiva, tj. nebyl pozorován rozdíl při porušení/chování spáry a kusového staviva. Současně došlo k porušení v ložné spáře. Navazující trhliny vycházely z rohů porušené oblasti cca pod úhlem 60° směrem ke spodním rohům stěny a také svislé dolů. Detail porušení vzorku je zřejmý z Obr. 15. Je patrno, že trhlina prochází skrz tvarovku i navazující styčnou spáru.
4.2.6 Vzorek II – odezva na vnášené zatížení a způsob porušení
U vzorku II bylo viditelné postupné zvyšování měřené deformace již při cyklování na hladině 350 Pa – obr. 14, kdy především ve třetím a čtvrtém cyklu docházelo k postupnému zvyšování zaznamenané deformace na všech snímačích a viditelnému smykovému posunu/porušení malty styčné spáry a zřejmě zaklesnutí zámku tvarovek. Nejvyšší zbytkové deformace byly opět zaznamenány v horní vodorovné linii vzorku.
Maximální únosnosti vzorku II bylo dosaženo na hladině působícího podtlaku 525 Pa; maximální zaznamenaná deformace konstrukce při této úrovni zatížení byla 5,9 mm (bod WA_6).
K porušení došlo náhle/křehce. Oproti vzorku I s maximálním promaltováním však bylo porušení realizováno ve významně menším počtu trhlin – obr. 15.

a)

b)
Obr. 15: Porušení vzorků; a) vzorek I, b) vzorek II
4.3 Zhodnocení a extrapolace dat získaných z full scale vzorků
4.3.1 Zhodnocení zjištěného chování vzorků
Vzorek II byl navržen s malým promaltováním spár, které tak svojí únosností významně limitovaly únosnost celé testované konstrukce. U tohoto vzorku došlo k dílčímu poškození a rozvoji trhlin již při zatěžovacích cyklech na hladinách 350 Pa, které byly doprovázeny nárůstem průhybu a též vysokými zbytkovými deformacemi po odtížení. Vzorek I toto chování nevykazoval.
Z výsledků obou zkoušek lze usuzovat na skutečnost, že způsob promaltování spár jednoznačně determinuje výsledek zkoušky, tj. mezní působící zatížení při porušení celistvosti vzorku příčky i její těsnosti.
4.3.2 Extrapolace chování testované konstrukce pro další cykly na hladině 350 Pa
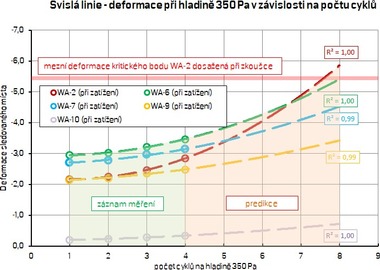
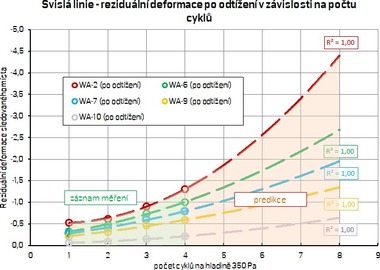
Na základě výsledků obdržených ze zatěžovací zkoušky vzorku II bylo dále extrapolováno očekávané chování pro případ, kdy by byla příčka opakovaně (ve shodném zatěžovacím schématu) namáhána na hladině působícího podtlaku 350 Pa. Očekávaný nárůst deformace měřených bodů ve střední svislé linii vzorku je zřejmý z obr. 16 a obr. 17.
Obr. 16: Extrapolace měřeného průhybu v jednotlivých bodech svislé střední linie příčky pro další cykly na hladině 350 Pa – vzorek II; a) deformace svislé linie při zatížení 350 Pa v závislosti na počtu cyklů, b) zbytková deformace po odtížení v závislosti na počtu cyklů
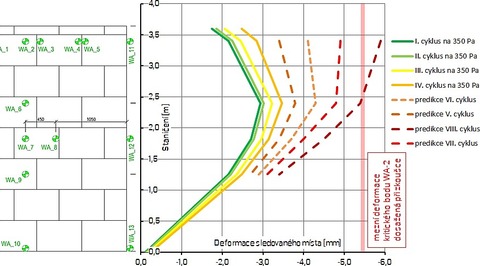
Obr. 17: Extrapolace chování vzorku příčky pro další cykly na hladině 350 Pa – průhyb ve střední svislé linii – vzorek II
Mezní deformace dosažená při kolapsu vzorku II byla cca 5,45 mm (WA-2), resp. 5,9 mm (WA-6). S ohledem na skutečnost, že oba testované vzorky dosáhly své mezní únosnosti při obdobné deformaci, lze usuzovat, že při cca sedmém až osmém cyklu na hladině 350 Pa by příčka s vysokou pravděpodobností selhala, a to bez navýšení zatížení. Toto konstatování je však platné pro modelovou příčku s danými charakteristikami6 a geometrií a též způsobem zatěžování7. Je též nutno vzít do úvahy, že se jedná o interpretaci výsledků zatěžovací zkoušky, tj. veškeré údaje/deformace jsou ve středních hodnotách.
5. Nelineární numerický model experimentální stěny
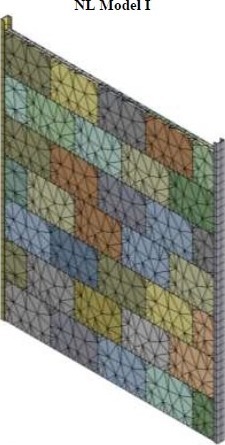
a)

b)
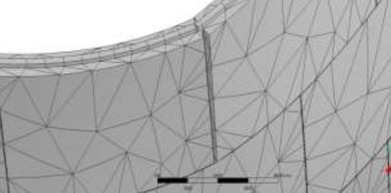
Obr. 18: Síť konečných prvků pro dva použité modely; a) NL model I, b) NL model II
Nelineární numerický model experimentální příčky měl za cíl simulovat chování vzorku II. Model plně respektoval skutečnou geometrii, způsob vyzdění a okrajové podmínky – tj. uložení vzorku a způsob vnášení zatížení. K výpočtům byl použit programový systém ANSYS a dále i program SCIA Enginner.
5.1 Geometrie
Modelovány byly vždy jednotlivé sádrové bloky v polohách dle experimentu, kdy tyto jsou vyzděny mezi ocelovými nosníky (profil U100). Styk jednotlivých příčkovek je modelován shodně se skutečným provedením, tj. s ozubem (pero + drážka) a promaltováním ložných i styčných spár v rozsahu dle vzorku II. Rozdíly v modelech NL I a NL II byly způsobeny pouze diskretizací řešené oblasti – viz obr. 18.
5.2 Materiálové charakteristiky nelineárního modelu
Materiály a odpovídající materiálové charakteristiky byly při výpočtu uváženy dle výsledků zjištěných experimentálně na odebraných vzorcích.
Pro simulaci otevření spáry (rozpojení kontaktu mezi maltou a bloky) byla využita funkce „Contact Debonding“ v kombinaci s použitím materiálu „CZM – cohezive zone material“. Dle zadaných charakteristik bylo materiálu CZM umožněno rozpojení v normálovém i tangenciálním směru. Parametry materiálu byly určeny na základě dopočtu limitního napětí a příslušného otevření spáry na základě provedených zatěžovacích zkoušek vzorků odebraných na pokusné stěně vyzděné z nových tvárnic MULTIGIPS.
| Spára | Normálová únosnost (odpovídající otevření spáry) | Tangenciální únosnost (odpovídající posun spáry) |
|---|---|---|
| Ložná | 0,89 MPa (0,22 mm) | 1,64 MPa (0,47 mm) |
| Styčná | 0,89 MPa (0,22 mm) | 0,77 MPa (0,32 mm) |
5.3 Výsledky výpočtu
K porušení došlo u obou modelů shodně s reálným experimentem rozevřením styčné spáry uprostřed vrchní řady tvarovek příčky, viz obr. 19. Porušení numerických modelů bylo dosaženo při mírně vyšším zatížení (cca 600 Pa oproti experimentálně stanoveným 525 Pa.
Výsledky z numerického modelu jsou vynášeny pro hladinu zatížení 350 Pa (očekávaná maximální hladina působícího podtlaku vyvolaného hasebním systémem) a 525 Pa (limitní zatížení dosažené při experimentu).
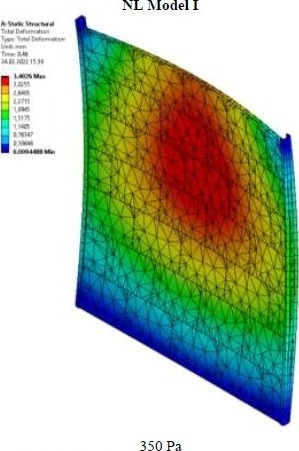
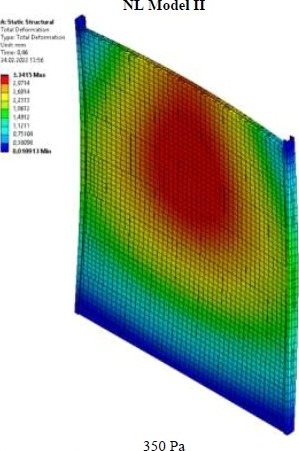
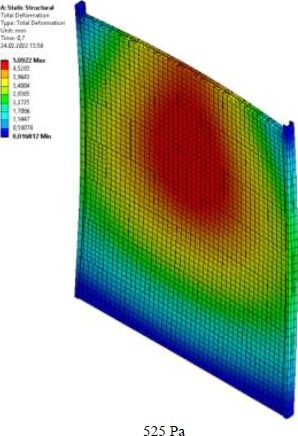
Na obr. 20 je zobrazena deformace konstrukce pro oba modely a úrovně zatížení 350 Pa (očekávaná hladina působícího přetlaku při požární události) a 525 Pa (kolaps vzorku při zkoušce). Rozdíl mezi modely I a II je zanedbatelný. Predikovanou deformaci lze porovnat s hodnotami stanovenými v průběhu experimentu (viz uvedené výsledky pro vzorek II prezentované v odstavci 5.2.6 – 3,5 mm ve čtvrtém cyklu zatížení na hladině 350 Pa; 5,9 mm při hladině 525 Pa).
Je zřejmé, že sestavené nelineární numerické modely vykazují velmi dobrou shodu se skutečným/pozorovaným chováním vzorku II při zatěžování, a to pro obě řešené hladiny působícího zatížení. Největší odchylka je při predikci deformace na hladině 525 Pa – teoreticky očekáváno 5,1 mm (odchylka cca 15 %); v případě hladiny 350 Pa je rozdíl predikce a skutečné deformace pouze cca 5 %.
a)
b)

c)
d)
Obr. 20: Predikovaná deformace konstrukce při hladinách působícího zatížení 350 Pa a 525 Pa; a) model NL I 350 Pa, b) model NL II 350 Pa, c) model NL I 525 Pa, d) model NL II 525 Pa
Z provedených výpočtů lze získat i řadu dalších informací, např. hodnoty hlavní tahové a tlakové napětí na povrchu vzorku a ozubu tvarovky, které umožní další verifikaci výpočtu pomocí experimentu.
Lze konstatovat, že provedená numerická simulace s vysokou přesností predikuje průběh a výsledky reálné zatěžovací zkoušky full scale vzorku II. Odchylky mezi modelem a skutečným proběhem zatěžovací zkoušky jsou velmi malé (do 15 %) a nelineární model tak lze považovat za výstižný a odpovídající. Mezní tahové napětí predikované modelem v kritické/rozhodující spáře při hladině zatížení 525 Pa je cca 0,77 MPa (maximální hodnota 0,84 MPa); tyto hodnoty je pro další vyhodnocení třeba uvážit jako střední. Zjištěné napětí je tak vyšší, než které by odpovídalo limitní hodnotě určené ze zkoušek malých vzorků.
6. Lineární numerický model experimentální stěny a skutečné konstrukce
Lineární numerický model (LIN model) byl vytvořen s cílem predikce chování experimentální konstrukce v lineární oblasti chování, tj. především pro hladinu působícího zatížení 350 Pa, a také pro ověření chování laboratorně netestovaných geometrií příčky. Lineárním modelem byla simulována odezva experimentální stěny (výška vzorku 3,65 m, šířka 3,0 m), ale dalších typů stěn, které se na konstrukci, která má být posuzována, vyskytují.
Lineární model však nelze spolehlivě využít pro oblast vyšších hladin působícího tlaku, kdy již dochází k porušení spár a tvorbě trhlin.
Řešeny byly dvě varianty idealizace zděné konstrukce příčky. V první variantě bylo uváženo dokonalé spolupůsobené tvarovky a malty – tzv. homogenní model chování. Tato idealizace je běžná při řešení obdobných konstrukcí v projekční praxi. Zjednodušeně ji lze uvážit za odpovídající vzorku I experimentální stěny realizované v areálu AdMaS, tj. modelu s maximálně vyplněnými spárami.
Druhá varianta výpočtu zohlednila reálnou rotační a smykovou tuhost styčných a ložných spár. Tuhosti byly stanoveny výpočtem na základě výsledků dle chování vzorků zjištěného na 1. RB. Tento model přibližně odpovídá variantě experimentální stěny s minimálně promaltovanou spárou (vzorek II), která je obdobná situaci in situ.
6.1 Geometrie modelu experimentální stěny a okrajové podmínky
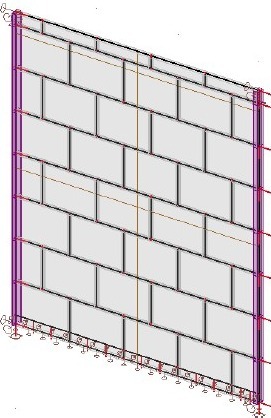
Výpočet simulující odezvu experimentálního vzorku příčky na hladinu působící tlaku 350 Pa plně respektoval skutečnou geometrii, způsob vyzdění a uvážené okrajové podmínky – tj. uložení vzorku a způsob vnášení zatížení v průběhu experimentu. Geometrie řešeného vzorku je patrna z obr. 21.
V lineárním modelu experimentální stěny testované v areálu AdMaS byly uváženy vstupní charakteristiky dle tab. 4.
a)
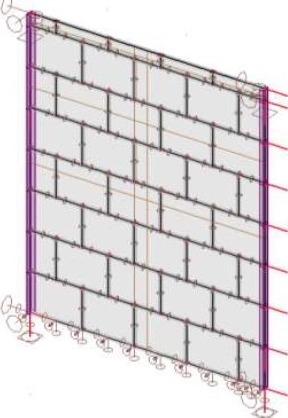
b)
Obr. 21: Lineární model – geometrie včetně uvážených okrajových podmínek; a) homogenní lineární model; b) lineární model se skutečnou tuhostí styčných a ložných spár

Obr. 22: Experimentální stěna vyzděná v areálu AdMaS pro ověření způsobu zdění s provedenými jádrovými odvrty ze zdicích bloků MULTIGIPS M80
V tab. 4 uvedené tuhostní charakteristiky spár byly stanoveny na základě výsledků zkoušek trámců a vývrtů odebraných na pokusné stěně, která byla zděna v laboratoři ze systému MULTIGIPS M80 – viz obr. 22. Smyková tuhost byla získána z „průměrných/obvyklých“ záznamů zkoušek smykové únosnosti vzorku vývrtu, rotační tuhost odpovídá chování zjištěnému ze zkoušek čtyřbodovým ohybem na vzorcích trámců.
| Materiál | Chování/model | Modul pružnosti/tuhost |
|---|---|---|
| příčkovka PROMONTA | lineární homogenní/ lineární s tuhostí spár | 3 730 MPa |
| rotační tuhost ložné spáry | lineární s tuhostí spár | 0,18 MNm/m/rad |
| rotační tuhost styčné spáry | lineární s tuhostí spár | 0,18 MNm/m/rad |
| smyková tuhost ložné spáry | lineární s tuhostí spár | 70 MN/m/m |
| smyková tuhost styčné spáry | lineární s tuhostí spár | 50 MN/m/m |
| konstrukční ocel (U-profil) | lineární homogenní/ lineární s tuhostí spár | 210 000 MPa |
6.2 Výsledky lineárního výpočtu experimentální stěny
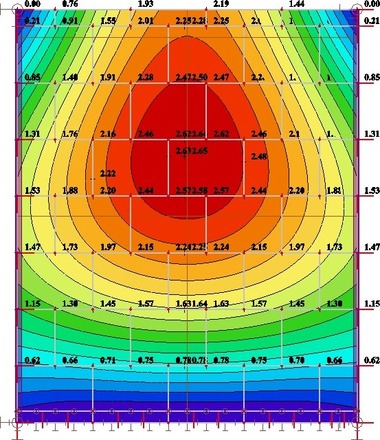
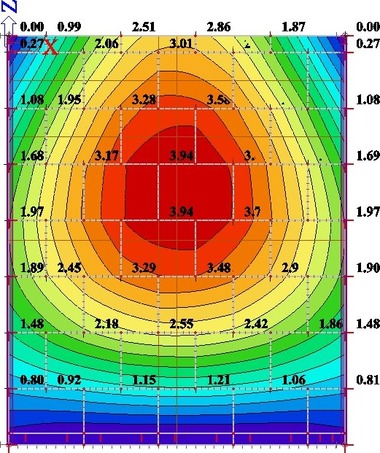
Na obr. 23 je zobrazen průběh deformace zatěžované konstrukce při uvážené hladině působícího tlaku 350 Pa. Maximální průhyb homogenního lineárního modelu je cca 2,6 mm. Očekávaný průhyb lineárního modelu se zohledněním tuhosti spár je cca 3,9 mm.
Obdržené hodnoty jsou v dobré shodě s výsledky full scale experimentů. Homogenní chování bez trhlin (platí pro tuto intenzitu působícího zatížení) vykazoval vzorek I. Při hladině zatížení 350 Pa (čtvrtý cyklus) byl zaznamenán průhyb 2,4 mm – tj. cca 92 % predikované hodnoty. Experimentální vzorek II vykazoval průhyb až 3,5 mm při čtvrtém cyklu na hladině zatížení 350 Pa, tato hodnota je cca 90 % predikované deformace (3,9 mm). Vytvořený lineární model je tedy možno hodnotit v definované oblasti namáhání jako vypovídající a lze jej využít i pro další extrapolace pro přímo netestované geometrie konstrukce.
Obr. 23: Lineární model experimentální stěny – průhyb; a) homogenní lineární model; b) lineární model se skutečnou tuhostí styčných a ložných spár
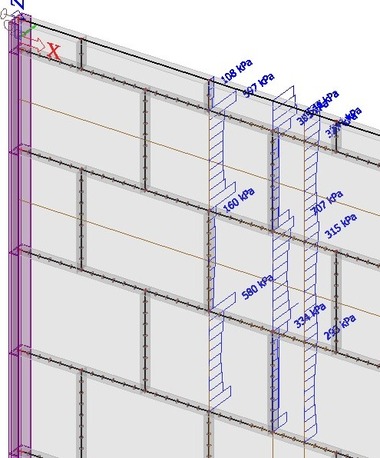
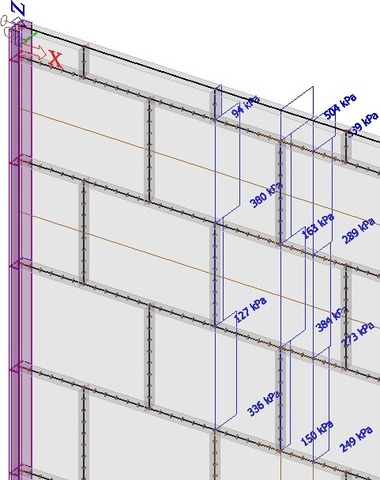
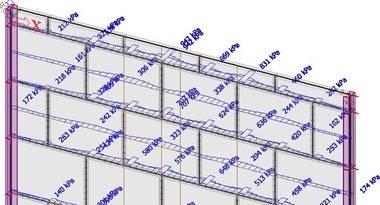
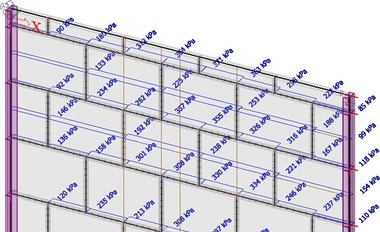
Pro oba modely byla též vyčíslena hlavní tahová napětí. Z výpočtů je zřejmé, že zásadní vliv na predikci rozdělení napětí na konstrukci má přijatý předpoklad o tuhosti spár. Maximální očekávané napětí na lineárním homogenním modelu je cca 0,36 MPa; v případě zohlednění reálné tuhosti spár je maximální špičkové napětí až cca 0,94 MPa. Jedná se však o špičky v oblastech styku ložné a styčné spáry.
Při uvážení rovnoměrného rozdělení napětí po délce spáry je působící tahové napětí v místě kritické styčné spáry cca 0,16 MPa, v přilehlé tvarovce pak až 0,5 MPa (horní dělená), resp. 0,4 MPa (běžná). Maximální napětí v ložné spáře (uváženo rovnoměrně na délku jedné tvarovky) je cca 0,37 MPa; viz obr. 24 a 25.
Obr. 24: Lineární model experimentální stěny se skutečnou tuhostí styčných a ložných spár – tahové napětí v kritických místech – svislé řezy; a) nezprůměrované hodnoty pro celou spáru/tvarovku; b) zprůměrované hodnoty pro celou spáru/tvarovku
Obr. 25: Lineární model experimentální stěny se skutečnou tuhostí styčných a ložných spár – tahové napětí v kritických místech – vodorovné řezy; a) nezprůměrované hodnoty pro celou spáru/tvarovku; b) zprůměrované hodnoty pro celou spáru/tvarovku
7. Závěr
Na základě všech v předchozím textu popsaných činností, tedy
- diagnostice aktuálního stavu konstrukcí příček PROMOMNTA in situ,
- odběru vzorků z posuzovaných stěn pro laboratorní rozbory (jádrové vývrty a trámečky/hranoly),
- vyzdění, zkouška a následné vyhodnocení velkoplošných vzorků,
- numerické modelování full scale testu,
bylo možno stanovit požadované charakteristiky zdiva příček PROMONTA. Klíčové mechanické charakteristiky zjištěné na odebraných vzorcích z konstrukcí jsou sumarizovány v tab. 1 (střední hodnota a charakteristická hodnota – 5% kvantil při uvážení lognormálního rozdělení); zásadní veličiny jsou stručně shrnuty též v tab. 5.
| Sledovaná charakteristika | Střední hodnoty (bez „nulových“ vzorků) [MPa] | Char. hodnoty (bez „nulových“ vzorků) [MPa] | Navýšení souč. ADM [–] |
|---|---|---|---|
| Pevnost v příčném tahu fct – vývrty, ložná spára | 0,236 | 0,149 | 1,5 |
| Pevnost v příčném tahu fct – vývrty, styčná spára | 0,139 | 0,055 | 1,5 |
| Pevnost v tahu za ohybu na hranolech fcf – ložná spára | 0,317 | 0,147 | 1,5 |
| Pevnost v tahu za ohybu na hranolech fcf – styčná spára | 0,202 | 0,084 | 1,5 |
| Pevnost ve smyku na vývrtech fs – ložná spára | 0,296 | 0,151 | 1,0* |
| Pevnost ve smyku na vývrtech fs – styčná spára | 0,162 | 0,101 | 1,0* |
| * Pozn.: Při full scale experimentu nedošlo k tomuto typu porušení, nelze tedy spolehlivě určit hodnotu součinitele. | |||
Dále lze vyslovit následující závěry
- z výsledků obou zkoušek full scale vzorků příček – experimentálních stěn – s odlišnou mírou promaltování je zřejmé, že způsob/kvalita promaltování spár jednoznačně determinuje výsledek zkoušky, tj. porušení celistvosti vzorku příčky i její těsnost;
- souběžně s full scale vzorky byly provedeny jádrové vývrty a vzorky trámců pro ověření odlišností mezi zdicími prvky na skutečné konstrukci a zdicími prvky MultiGips spojenými maltou MultiGips Fugenfuller použitými v průběhu full scale experimentu. Lze konstatovat, že výsledky dosažené na vzorcích s minimálním vyplněním spár jsou srovnatelné s výsledky na neporušených vzorcích jádrových vývrtů odebraných ze skutečné konstrukce provedené z prvků PROMONTA;
- experimentální vzorek II při cyklování na hladině 350 Pa vykazoval podstatný nárůst deformace při každém cyklu. Lze usuzovat, že při opakování cyklů na hladině 350 Pa by příčka s vysokou pravděpodobností selhala bez dalšího navýšení zatížení. Je tak zřejmé, že s vysokou pravděpodobností není možné reálnou konstrukci opakovaně zatěžovat hladinou působícího tlaku 350 Pa bez kumulace poškození v konstrukci a její postupné degradace;
- sestavený nelineární numerický model s velkou shodou predikuje chování experimentálního vzorku II testovaného v laboratoři; porušení bylo dosaženo shodným způsobem – tahem za ohybu ve styčné spáře. Veškeré vstupy nelineárního modelu byly pro možnost srovnání s reálnými vzorky uváženy ve středních hodnotách. Lze porovnat působící hlavní tahové napětí v kritické spáře při kolapsu vzorku (cca 525 Pa) a požadované hladině působícího tlaku na konstrukci (350 Pa) – tento poměr je cca 1,51 a je ve velmi dobré shodě se zjištěním zkoušky vzorku II;
- při zohlednění způsobu porušení vzorku II při experimentu a též výsledků predikce nelineárního modelu lze uvážit zvýšení středních hodnot charakteristik tahu za ohybu, resp. příčného tahu stanovenému na odebraných vzorcích jádrových vývrtů/trámců součinitelem 1,5 (viz tab. 5)8. Toto konstatování je však platné pouze pro testovanou konstrukci, daný způsob statického zatěžování a při full scale testech zjištěný způsob porušení – tj. uvážené geometrické rozměry, střední hodnoty sledovaných charakteristik, porušení tahem ve spárách a statické působení aplikovaného zatížení.
- lineární numerický model byl sestaven za účelem predikce chování experimentální konstrukce testované v laboratoři při působení zatížení v lineární oblasti chování, tj. především pro hladinu působícího zatížení 350 Pa9. Model vykazuje dobrou shodu s pozorovaným chováním experimentálního Vzorku II;
- lineární model lze využít pro prognózu chování příček PROMONTA s jinou geometrií při nižších hladinách namáhání.
Při interpretaci výše uvedených závěrů je zásadní uvážit, že v případě výsledků experimentů (není-li uvedeno jinak) je prezentována střední hodnota sledované charakteristiky (např. únosnost full scale experimentální stěny). Vzorky materiálu odebrané z testovaných experimentálních stěn v laboratoři neobsahovaly „nulové“ hodnoty, tj. vzorky porušené již při odběru. V reálné konstrukci se však tato místa vyskytují a nelze tak vyloučit jiné (horší) chování.
8. Poděkování
V návaznosti na možné (a v některých případech nutné) dodatečné zesílení podobného typu konstrukcí bude možno využít výsledky projektu Udržitelná výroba kompozitních materiálů, který řeší PREFA KOMPOZITY, a.s. a Ústav betonových a zděných konstrukcí FAST VUT v Brně, a který byl podpořen Technologickou agenturou ČR, TA1223S04000.
9. Literatura
- Podklady k příčkám PROMONTA
- ČSN ISO 13822 (730038) Zásady navrhování konstrukcí – Hodnocení existujících konstrukcí; 2015
- ČSN EN 1996-1-1 (731101) Navrhování zděných konstrukcí – Část 1-1: Obecná pravidla pro vyztužené a nevyztužené zděné konstrukce; 2013
- Podklady k sádrovým blokům MULTIGIPS. VG-ORTH GmbH & Co. KG
- Podklady k sádrové maltě MultiGips Fugenfuller. VG-ORTH GmbH & Co. KG
- Štěpánek, P. – Girgle, F. – Cikrle, P. – Daněk, P. – Kostiha, V. – Januš, O.: Stanovení fyzikálně mechanických parametrů zděné konstrukce stěny na základě velkorozměrové zkoušky. Konference Statika staveb, ČKAIT Plzeň, 6.–7. 9. 2023, ISBN: 978-80-88265-43-6
Text byl zařazen do sborníku [6]; redakcí TZB-info bylo vyžádáno jeho publikování, text byl po recenzi redakce upraven.
Poznámky
1 V tomto případě bude používán i termín „full scale test“. ... Zpět
2 Systém, jehož autorem byl prof. Melcher, funguje na principu hermeticky uzavřené obálky, jejíž stěny tvoří ocelová stolice a zkušební vzorek. Po utěsnění vzorku pomocí membrány je vývěvou postupně odsáván vzduch a vytvářen podtlak. Tímto je dosaženo rovnoměrné plošné zatížení působící na celou plochu zkušebního vzorku. ... Zpět
3 Zatěžovací schéma bylo voleno s přihlédnutím na objednatelem definovaný způsob hasebního zásahu a hladinu maximálního přípustného podtlaku/přetlaku působícího na konstrukci 350 Pa. ... Zpět
4 snímače WA_2; WA_6; WA_7; WA_9 a WA_10 dle obr. 10. ... Zpět
5 Jako limitní byla uvážena ztráta celistvosti vzorku, tj. oddělení/porušení jednotlivých příčkovek PROMONTA při souběžném značném otevření/posunu spár, přítomnost průběžných trhlin a skokovému snížení ohybové tuhosti vzorku doprovázenému výrazným poklesem tlaku ve vakuovací komoře; dosažení limitní hodnoty zatížení bylo doprovázeno/signalizováno i výrazným akustickým efektem. Těsnost, s ohledem na provedení zkoušky vakuováním a opláštění vzorku vzduchotěsnou membránou, nemohla být přímo měřena, na dosažení jejího limitu lze však s ohledem na způsob porušení vzorku spolehlivě usuzovat. Tuto skutečnost dokumentovalo i porušení vzorku, které bylo zjištěno a zaznamenáno po ukončení zkoušky a odstranění neprodyšné membrány na vnějším povrchu zkoušeného vzorku. ... Zpět
6 Tj. způsobem promaltování spár ... Zpět
7 V průběhu zatěžovací zkoušky bylo zatížení cyklováno mezi maximální a nulovou hodnotou, nedocházelo k změně smyslu zatížení, tj. změně v lokalizaci tažených a tlačených vláken v průřezu. Významně horší situace, tj. nižší únosnost/počet cyklů, by nastala v případě, kdy by docházelo k oscilaci zatížení kolem nulové hodnoty a tedy ke změně smyslu namáhání. ... Zpět
8 Tato skutečnost je způsobena především rozdílným působením/chováním při zatěžování malých vzorků odebraných přímo z konstrukce a celé full scale experimentální stěny (tzv. size-efekt); případně možného negativního ovlivnění vzorků při odběru z konstrukce. ... Zpět
9 Model nelze věrohodně využít pro oblast vyšších hladin působícího tlaku, kdy již dochází k porušení spár a tvorbě trhlin a tedy nelineární odezvě konstrukce na vnášené zatížení. ... Zpět
Článek je cennou studií v oblasti zkoušení zdiva a numerických simulací zděných konstrukcí a současně inspirativní ukázkou inženýrského přístupu k návrhu, resp. posouzení konstrukce, pro jejíž hodnocení není dostačující opora v normě. Drobné změny byly akceptovány, doporučuji k vydání.