Ověřování materiálových vlastností vláknobetonu

Abstrakt

Dlouhodobé studium vláknobetonu, tj. kompozitního materiálu s cementovou matricí, jehož struktura je vyztužena zpravidla náhodně rozptýlenými vlákny (nejčastěji ocelovými), prokazuje dobré mechanické i další technické vlastnosti, které umožňují jeho využití pro nosné konstrukce. To stimuluje vývoj metod, pokud možno nedestruktivních či málo invazivních, pro vyšetřování jeho struktury, podmiňující klíčové mechanické vlastnosti, např. odolnost vůči porušení při tahovém namáhání. Tento článek, vycházející z výzkumných aktivit Fakulty stavební VUT v Brně, přináší přehled dostupných metod, zejména přímých metod vycházejících ze zpracování obrazů a nepřímých metod využívajících měření elektromagnetických veličin.

1. Úvod

Vláknobeton, v mezinárodní terminologii obvykle FRC (což je zkrácený anglický název „Fibre Reinforced Concrete“) je kompozitní materiál s cementovou matricí doplněnou vlákny, které mají zlepšovat jeho mechanické i další technické vlastnosti, zejména omezovat možnost vzniku trhlin při tahovém namáhání, včetně vlivu objemových změn matrice, zejména smršťování v jejích raných stádiích, zlepšovat lomovou houževnatost, případně (v závislosti na použitém typu vláken) i požární odolnost. Vlákna mohou být polyetylenová, polypropylenová, polyesterová apod. různých velikostí a tvarů, ale i skelná či (velmi často) kovová. Z kovových vláken se nejvíce používají ocelové drátky; takový vláknobeton se pak označuje jako drátkobeton. Cílem technologie přípravy vláknobetonu bývá (aspoň zhruba) nahodilé rozložení směrů vláken, které umožňuje (přinejmenším v prvním přiblížení) nahlížet na materiál jako na makroskopicky homogenní a izotropní, neboť záměrné dosažení jiného, předem zadaného rozložení je (na rozdíl od betonu s klasickou či předpjatou výztuží) technologicky velmi problematické; podrobněji viz [Vít].

Ještě v nedávné minulosti byly vláknobetony obecně považovány hlavně za vhodnou alternativu prostého betonu v případech, kdy bylo potřebné předem omezit vznik mikro- či makrotrhlin, třeba jen z estetických důvodů. V posledních letech se však díky příznivým mechanickým vlastnostem, zejména v případě drátkobetonů, rozmáhá i jejich používání pro konstrukční účely: nejen pro průmyslové podlahy a prefabrikované kanalizační trouby, ale přes základové desky obytných staveb či základy regálových systémů ve skladech až po zdánlivě kuriózní uplatnění pro pingpongový stůl, sestavený z tenkostěnných prvků z ultravysoko-pevnostního drátkobetonu podle [Sla].

Nárůst četnosti aplikací vláknobetonu pro konstrukční účely reflektují postupně i technické normy. Působení vláken přidaných do cementové matrice lze zohlednit např. podle německé směrnice [Daf], která na úrovni zákonného předpisu doplňuje normu [DIN], v České republice však vhodná technická norma dosud chyběla. Tuto mezeru se nyní snaží zaplnit trojice návrhů [Č51], [Č52] a [Č53], z nichž první je věnován klasifikaci vláknobetonů, druhý a třetí pak jejich zkoušení v čerstvém a ztvrdlém stavu; o jejich přípravě zevrubně informuje [Han]. Při vyšetřování výsledných mechanických vlastností vláknobetonu se klade důraz na zkoušku trámce o velikosti 150 × 150 × 700 mm čtyřbodovým ohybem na rozpětí 600 mm; určují se pevnosti v tahu i) při vzniku makrotrhliny za předpokladu kvazielastického chování materiálu, ii) při průhybu trámce 0,5 mm za předpokladu elastického chování materiálu v tlačené oblasti a plastického chování v oblasti tažené, iii) při průhybu trámce 3,5 mm za předpokladu plně plastického chování materiálu. Ještě podrobněji, s četnými odkazy na [Daf], se věnuje návrhu vhodných konstitutivních vztahů pro vláknobeton a následnému vyčíslování únosnosti materiálu v ohybu, smyku a protlačení i určení šířky trhlin [Pou]. Spoléhá se opět na zkoušku v tahu za ohybu, pracuje s bilineárními a trilineárními závislostmi mezi napětím a přetvořením a dospívá nakonec k devíti semiempirickým vztahům pro výpočet zmíněných veličin, obsahujících řadu opravných součinitelů, jež se snaží zohlednit vliv podrobněji nestudovaných fyzikálních a chemických procesů i geometrických charakteristik včetně jejich částečně stochastického charakteru a možné degradace při dlouhodobém namáhání.

Důkladné fyzikální, matematické a numerické modelování naznačených procesů se zohledněním dostupných údajů o mikrostruktuře kompozitního materiálu na základě obecných principů klasické termomechaniky, jak se jím (včetně raného stadia existence materiálu, jeho dlouhodobého a extrémního namáhání) zabývají [Gaw¹] a [Gaw²], se dosud pohybuje na pomezí mezi základním a aplikovaným výzkumem s řadou otevřených problémů, a nemůže tak být aktuálním východiskem pro praktické navrhování a realizaci staveb. Stanovení mechanických vlastností podle existujících či připravovaných technických norem, na něž odkazují [Pou] i [Han], nicméně vyžadují přinejmenším důkladné destruktivní zkoušky vzorků v dobře vybavené laboratoři. Žádané jsou nicméně i postupy, které by umožnily ověření vlastností drátkobetonu na již realizovaném stavebním díle, nejlépe zcela nedestruktivní, realizovatelné in situ, nebo aspoň málo invazivní z hlediska nároků na odběr vzorků; těmto postupům se budeme věnovat v následujícím textu.

2. Struktura vláknobetonu a jeho mechanické vlastnosti

Nehledě na úroveň obecnosti výpočtových modelů, lze jako základní charakteristiky, jež podmiňují dosažení žádoucích mechanických vlastností vláknobetonu pro konkrétní konstrukční uplatnění, vymezit:

1. objemový podíl vláken,
2. rozložení směrů vláken,
3. tvar a velikost vláken,
4. materiálové vlastnosti vláken i cementové matrice,
5. soudržnost mezi vlákny a cementovou matricí.

Známe-li předem c) a d) (tj. důvěřujeme-li tomu, že při přípravě vláknobetonu byly použity předepsané komponenty), je možné za předpokladu dokonalé soudržnosti e) přinejmenším odhadovat hodnoty materiálových charakteristik výsledného kompozitu pomocí výpočtové homogenizace, vedoucí k jistým efektivním hodnotám, jejichž praktická validace pomocí naměřených údajů je nicméně žádoucí. Obvyklé matematické teorie homogenizace, prezentované v [Cio], jmenovitě tzv. dvouškálová homogenizace, pracují teoreticky s deterministickými, přesně periodickými materiálovými strukturami, přičemž rozměry mikrostrukturálních objektů mají být natolik zanedbatelné, že je lze limitně zkoumat jako blížící se k nule. Zeslabení některého z uvedených předpokladů, zejména odstranění periodicity či připuštění stochastického charakteru materiálové struktury, je sice možné, ale vede k mimořádně komplikované matematické teorii konvergence na tzv. homogenizačních strukturách, diskutované v [Ngu], od níž je k praktickým výpočtovým algoritmům dosud velmi daleko. I pro dvouškálovou konvergenci je třeba pro určení efektivních materiálových charakteristik většinou řešit pomocný problém v podobě parciální diferenciální rovnice s periodickými okrajovými podmínkami; analytické výrazy jsou k dispozici jedině pro extrémně jednoduché (zpravidla nerealistické) případy, např. pro (předem předpokládaný) stejný směr veškerých vláken. Alternativně se proto v praxi často vychází ze zjednodušených předpokladů, zejména z různých variant teorie směsí – srov. [Gio]. Závažné důsledky by nicméně mohlo mít porušení e); důkladnou relevantní analýzu lze najít v [Rud], str. 39.

V tomto článku se nadále soustředíme na zjišťování a) a b) ztvrdlého drátkobetonu realizovaných konstrukcích. Pro větší přehlednost budeme u jednotlivých přístupů hodnotit samostatně:

1. rozsah nezbytného zásahu do již hotové konstrukce,
2. dostupnost a nákladnost experimentálních i výpočtových prostředků,
3. robustnost použití a očekávatelnou přesnost výsledků,
4. možnost současného zjišťování a) i b).

Veškeré fotografie i grafické výstupy na obr. v tomto článku pocházejí z laboratoří Fakulty stavební VUT v Brně.

3. Destruktivní zkoušení

Obr. 1: Ukázka destruktivního ověřování množství drátků v odebraném vzorku drátkobetonu (nalevo). Využití magnetických vlastností drátků pro jejich sběr (napravo).

S ohledem na akcentování málo invazivních a nedestruktivních přístupů a) a b) zařazujeme tuto stručnou část pouze z přehledových a historických důvodů. Praktické zkoušení dokumentuje ilustrativní obr. 1.

Zhodnocení:

1. Je nutno odebrat dostatečné množství vzorků pro destrukci v laboratoři, což může představovat nepřípustný zásah do realizované konstrukce.
2. Zkoušení je pro běžná vlákna, zejména pro ocelové drátky, levné: po poněkud pracné destrukci vzorku stačí zjistit hmotnost uvolněných vláken (známe-li jejich objemovou hmotnost). Jen obtížně realizovatelné by bylo nicméně separování mikrovláken z matrice.
3. Pro konkrétní vzorek s libovolným typem vláken lze dosáhnout až absolutní přesnosti a).
4. Informace o původních směrech vláken se destrukcí vzorku ztratí, takže b) zjišťovat vůbec nelze.

4. Metody založené na zpracování obrazů

Dostupnou skupinu přímých nedestruktivních metod představuje pořizování dvourozměrných či třírozměrných snímků testovaných vzorků a jejich následné vyhodnocování různými metodami zpracování obrazů (označovanými, často i v českých textech, souhrnně jako „image processing“). Žádoucí jsou údaje o struktuře nejen o povrchu vzorku a blízké oblasti, ale o celém objemu vzorku. Příkladem dvourozměrného zpracování obrazů je tak opakované vyhodnocování promyšleně pořizovaných řad fotografických či rentgenografických snímků, na rozdíl od výrazně nákladnějšího využití hardwarových i softwarových vymožeností počítačové tomografie (známé pod zkratkou CT, tj. „Computer Tomography“).

4.1. Zpracování dvourozměrných fotografických či rentgenografických snímků

Využití fotografického i radiografického snímkování představuje dnes již klasický nedestruktivní přístup k získávání informací o struktuře vláknobetonu, zejména b). Zdánlivě nejjednodušší pořizování běžných fotografií vzorků využívá odlišné světelné odrazivosti lesklých vláken a matné cementové matrice; použitelnost přístupu přinejmenším pro kovová vlákna je tak zřejmá. Vzorky se v dostatečném množství připravují pilami na beton s vodním chlazením; zařazení tohoto přístupu mezi málo invazivní je tedy problematické. Pořizování snímků vyžaduje promyšlenou přípravu: osušení řezných ploch, fixování zdroje světla, speciální opatření k potlačení distorzního zkreslení atd. Vyhodnocení snímku se následně provádí netriviálními metodami obrazové analýzy; např. [Flá] pro tento účel používá mimo běžný komerční software pro úpravu fotografií i vlastní program, vyvinutý v prostředí MATLABu.

Bez složité přípravy nařezaných vzorků se obejde radiografické snímkování. Podrobně se tomuto přístupu věnuje [Hob¹], kde se přímou detekcí polohy drátků z jednotlivých snímků zjišťuje jejich počet, příslušný jednotlivým třídám úhlů v rovině, z čehož lze následně sestavovat tzv. směrové růžice. Na grafických výstupech tohoto typu (jsou-li k dispozici v dostatečně reprezentativním množství) lze tak snadno kontrolovat, zda byla technologickým postupem dodržena makroskopická izotropie materiálu, důležitá pro zamezení vzniku trhlin při tahových namáháních z různých směrů. Problémy nicméně mohou být s idealizovanou makroskopickou homogenností materiálu, zejména při soustředění vláken (zejména při jejich poměrně nízkém objemovém podílu v materiálu), třeba i (přibližně) nahodilých směrů, do několika center, mezi nimiž zůstává nevyztužená matrice.

Věrohodné usuzování na prostorové rozložení vláken z jednoho snímku (či jejich malého množství), jakkoliv by bylo při známé délce vláken stejného typu teoreticky (klasickými metodami deskriptivní geometrie) možné, není realistické s ohledem na obvyklou kvalitu snímků a technologický postup při přípravě vláknobetonu. Detekce polohy vláken musí být dostatečně robustní, aby zpracovala i různě zakřivená vlákna, případně i zmiňovaná nežádoucí centra.

Obecně je takové přímé zjišťování polohy vláken pracné, a tak se hledají alternativní, podstatně rychlejší přístupy – srov. [Kär]. Pro vyhodnocení rovinných snímků se nabízí rychlá diskrétní Fourierova transformace (algoritmus FFT, tj. „Fast Fourier Transform“). Uvažujeme-li (pro jednoduchost) úrovně šedé (bílé až černé) barvy f(x,y) na čtvercovém obrazu obsahujícím N × N pixelů (hypotetická limitní formulace s N → ∞ převádí součty na integrály, odpovídající klasické spojité transformaci), má diskrétní přímá Fourierova transformace jednoduchý (i když stále komplexní) tvar

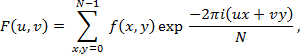(1)

přičemž odpovídající zpětnou transformaci lze vyjádřit ve velmi podobném tvaru

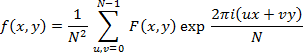(2)

s tím, že veškeré informace potřebné k vytvoření směrové růžice obsahuje příslušné spektrum P(u,v) = |F(u,v)|²; podrobnosti interpretace (1) a (2) včetně instruktivních příkladů, pocházejících z konkrétních měření, srovnatelných s [Hob¹], lze najít v [Val³] a [Val⁴]. Zde uvádíme na obr. 2 jen ukázku rentgenografického snímku, odpovídající spektrum a výsledné dvourozměrné rozložení směrů, sestavené vlastním programem v MATLABu.

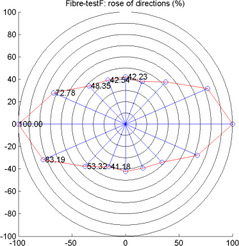Obr. 2: Rentgenografický snímek drátkobetonu (nalevo). Spektrum P získané algoritmem FFT (uprostřed). Výsledné rozložení směrů drátků (napravo).

Zhodnocení:

1. Fotografické snímkování je přinejmenším částečně destruktivní. Při radiografickém snímkování není sice potřebné řezat vzorky, nicméně snímkování nelze provádět in situ, takže odběr vzorků je rovněž nezbytný.
2. Fotografické snímkování je nenákladné, i když potřebuje kvalitní fotografický přístroj s příslušenstvím včetně programového vybavení. Radiografické snímkování už vyžaduje specializovanou laboratoř, nicméně příslušná zařízení nejsou (přinejmenším ve srovnání s tomografickou technikou) příliš nákladná.
3. Přesnost b) značně závisí na kvalitě a případné další úpravě snímků. Zejména u fotografických snímků nelze tento postup doporučit pro nekovová (málo lesklá) vlákna.
4. S přiměřenou přesností lze zjistit pouze b); odhadování a) je problematické, i když ne zcela nemožné.

4.2. Zpracování trojrozměrných tomografických snímků

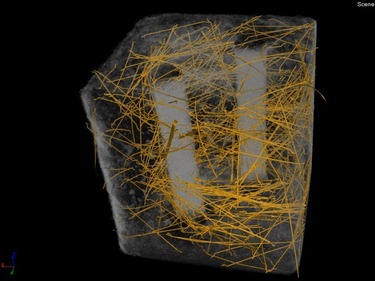Obr. 3: Analýza vzorku na průmyslovém tomografu (nalevo). Výsledné rozložení směrů drátků (napravo).

Vyšší vývojový stupeň zpracování obrazů představuje průmyslová počítačová tomografie. Vhodná zařízení (jiná než zařízení pro lékařské aplikace, pracující na obdobném fyzikálním principu – podrobněji viz [Wei]) pro testování speciálních typů vláknobetonových vzorků (v předepsaném tvaru kvádru či válce) jsou k dispozici mj. na výzkumných centrech CEITEC („Central European Institute of Technology“) VUT a AdMaS („Advanced Materials, Structures and Technologies“) FAST VUT. Jejich využití je nicméně výrazně omezeno nutností přípravy speciálních vzorků (a tedy praktickou nepoužitelností in situ) a značnými finančními náklady, jakož i nutností práce se specializovaným hardwarem a softwarem, jen obtížně přizpůsobovatelným vlastním potřebám. Pro konkrétní vzorek je nicméně tento přístup schopen poskytnout zcela přesné údaje a) i b) (v případě b) včetně prostorového zobecnění směrových růžic), což jej předurčuje jako vhodný ke kalibraci jiných, zejména nepřímých metod, konkrétně měření intenzity stacionárního magnetického pole Hallovou sondou podle levé části obr. 4. Srovnání obou zmiňovaných přístupů je důkladně provedeno v [Hob²].

Obr. 4: Zjišťování intenzity magnetického pole ve vzorku Hallovou sondou (nalevo). Elektromagnetická analýza rozložení drátků ve vzorku (napravo).

 

Obr. 5: Modelování intenzity magnetického pole pro známé rozložení drátků (nalevo). Pseudonáhodné generování polohy vláken (napravo nahoře) pro zadané rozložení směrů a detail jejich kontaktu (napravo dole).

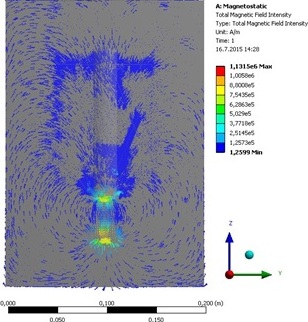
Další možnosti využití přesných údajů o poloze vláken z tomografických snímků jsou diskutovány v [Val²]. Dosud v úplnosti nepublikovaný algoritmus softwarového generování polohy drátků ve směrech odpovídajících zadanému pravděpodobnostnímu rozdělení, navazující na výsledky [Pos] a implementovaný v MATLABu, představuje východisko pro výpočtové modelování a simulaci nepřímých měření, zejména elektromagnetických, metodami teorie her, např. metodou Monte Carlo, s využitím standardních technik metody konečných prvků a objemů. Pravá část obr. 5 dokládá použitelnost tohoto přístupu i pro extrémně vysoký (zde jen hypotetický) objemový podíl drátků ve vzorku. Levá část téhož obr. předvádí možnost modelování rozložení intenzity stacionárního magnetického pole, generovaném permanentním magnetem při testování Hallovou sondou (viz dále), s podporou softwaru ANSYS ve vzorku, v němž je předem přesně známa poloha vláken, získaná zpracováním trojrozměrného tomografického snímku.

Zhodnocení:

1. Zřejmým destruktivním prvkem je nutnost pečlivé přípravy vzorků předepsané velikosti a tvaru.
2. Zkoušení vzorků (i jednotlivých) je obecně velmi nákladné; příslušná zařízení jsou nicméně např. na VUT v Brně dostupná pro výzkumné účely.
3. Přesnost a) i b) pro daný vzorek může být až absolutní, opakovatelnost experimentu však omezuje mj. vysoká cena za provoz zařízení včetně specializovaného vyhodnocovacího softwaru. Grafický výstup zobecněných trojrozměrných směrových růžic pro b) není příliš názorný. Metoda je tak vhodná zejména jako srovnávací s jinými, podstatně méně nákladnými (nejlépe za použití stejného vzorku).
4. Přesné výsledky a) i b) lze získat v podobě textového výstupu pro další zpracování vlastními programovými prostředky.

5. Metody založené na elektromagnetických měřeních

Vzhledem k obecné nepřijatelnosti destruktivního testování, nedostatečné informaci o a) z fotografických i rentgenografických snímků a nákladnosti a omezenosti tomografického snímkování je účelné hledat alternativní, pokud možno nedestruktivní metody pro identifikaci a), nejlépe i pro současnou identifikaci b). Tyto metody jsou vesměs nepřímé, tedy vycházející z analogie s jinými fyzikálními procesy. Elektromagnetické metody, vhodné především pro kovová vlákna, jsou založeny na rozdílné (relativní) magnetické permeabilitě, resp. dielektrické permitivitě, případně i dalších materiálových charakteristikách vláken a matrice v kompozitním materiálu. Aktuálnost vývoje takových metod, jejich rozšíření v posledních letech a možnost jejich podrobnější klasifikace dokumentuje [Fai]. Navzdory jisté nevýhodě, kterou představuje dosti obtížný identifikační problém stanovení efektivních hodnot zmiňovaných charakteristik na základě výpočtové homogenizace, jehož úskalí jsme zmínili už ve druhé části tohoto článku (pro mechanické charakteristiky), případně obcházení tohoto problému vytvářením kalibračních křivek pro velmi speciální typy vláknobetonu pro dostatečně rozsáhlé soubory experimentálních údajů, se tyto metody jeví jako progresívní.

5.1. Analýza stacionárního magnetického pole

V rámci elektromagnetických měření se jako nejjednodušší nabízí analýza stacionárního magnetického pole, jejíž možnou praktickou realizaci, fungující na základě Hallova jevu, ukazuje levá část obr. 4: permanentní magnet generuje magnetické pole, jehož zeslabení, měřené v jistých (obezřetně volených) vzdálenostech od magnetu, vypovídá zprostředkovaně o a), méně již (neprovádí-li se experiment opakovaně v různých směrech) o b). Při představě o možné homogenizaci problému jde na makroskopické úrovni (přibližně) o řešení Laplacovy rovnice pro intenzitu magnetického pole, kde příslušná magnetická permeabilita vystupuje jen v okrajové podmínce; porovnání [Val⁴] s realističtější výpočtovou konfigurací včetně zahrnutí Hallovy sondy nicméně neukazuje významnou systémovou chybu takové idealizace.

Uvažujme stejná (přibližně) válcová vlákna zjednodušená (kvůli hladkosti hranice) na protáhlé rotační elipsoidy, přičemž a a b jsou délka hlavní osy a (stejná) délka obou vedlejších os. Snadno pak můžeme definovat dva tvarové parametry: ζ = a/b a ϑ, jejž lze dopočítat ze vztahu 1 = ζ ² − ϑ ². Mimoto potřebujeme pracovat s (relativní) permeabilitou vláken μ_s, kterou jejich výrobci zpravidla negarantují, a s (relativní) předem známou permeabilitou matrice μ_c (prakticky nejčastěji jednotkovou), jakož i s efektivní (relativní) permeabilitou směsi.

V rámci této idealizace lze pro dostatečně nízký objemový podíl vláken ξ v kompozitním materiálu (výrazně menší než na pravé části obr. 5, v praxi zhruba do 1 %) použít na základě analýzy [Gio], vycházející z teorie pro makroskopicky izotropní materiál explicitní vzorec

(3)

v němž vystupují pomocné charakteristiky

(4)

Identifikace μ jako funkce ξ, založená na (3) (všimněme si, že μ je na pravé straně (3) obsaženo jednak přímo, jednak je též skryto v M prostřednictvím (4)), pro neznámou hodnotu μ_s na základě měření intenzity magnetického pole s využitím numerické metody nejmenších čtverců představuje nicméně netriviální inverzní matematický problém, jehož podrobnou analýzou se s využitím teoretických výsledků [Val¹] zabývá [Val³]. Pro makroskopicky anizotropní materiál se navíc vztah (3) výrazně zkomplikuje, neboť ve výpočtech podle [Gio] se objeví eliptické integrály, které nelze řešit analyticky.

K získání věrohodných (nejen přibližně informativních) výsledků, zejména vztahujících se k rozložení vláken hlouběji pod povrchem masívní konstrukce, je třeba provádět řadu vývrtů do hotové konstrukce; u laboratorních vzorků lze provádět i vývrty ve třech nezávislých (nejlépe navzájem kolmých) směrech s očekáváním, že obdobné nebo odlišné výsledky potvrdí nebo vyvrátí v (3) skrytý předpoklad izotropie. V rámci analýzy stacionárního magnetického pole už nicméně nemáme pro případnou lepší organizaci experimentu k dispozici žádné další volitelné parametry.

Zhodnocení:

1. Metodu lze považovat za málo invazivní, pro zjištění množství (a případně rozložení) vláken hlouběji pod povrchem je však vždy zapotřebí provádět umělé vývrty do konstrukce.
2. Mimo náklady na pořízení Hallovy sondy jsou experimentální i výpočtové náklady nízké.
3. Omezením metody je rychlé zeslabování intenzity magnetického pole v nevelké vzdálenosti od permanentního magnetu. Pro navzájem blízké hodnoty magnetické permeability vláken a matrice (což naštěstí nelze očekávat u kovových vláken) je metoda nevhodná, stejně jako v případě vysoký podíl ξ pro jakákoliv vlákna.
4. Dosti spolehlivě lze určit a) za předpokladu makroskopicky izotropní struktury materiálu. Naproti tomu b) lze jen zprostředkovaně odhadovat.

5.2. Analýza harmonicky buzeného nestacionárního elektromagnetického pole

Překonání kritizovaných nedostatků analýzy stacionárního elektromagnetického pole je (přinejmenším teoreticky) možné přechodem k analýze nestacionárního elektromagnetického pole. Mimo intenzitu magnetického pole H zde můžeme pracovat i s intenzitou elektrického pole E a s potřebnými materiálovými charakteristikami: dielektrickou permitivitou ε, elektrickou vodivostí σ a magnetickou permeabilitou μ (ty mohou být obecně maticové, zde je však pro jednoduchost výkladu budeme uvažovat jako skalární). Kompletní fyzikální a matematická analýza nicméně vede k počátečním a okrajovým úlohám pro soustavu Maxwellových parciálních diferenciálních rovnic, která dosud (s ohledem na svou výraznou nelinearitu) skrývá i různá teoretická úskalí včetně nejasností v konvergenci posloupností přibližných numerických řešení, nemluvě již o identifikačních problémech. Za řady zjednodušujících předpokladů lze nicméně odvodit výsledné rovnice (pro podrobný postup viz [Val²])

(5)

v nichž tečky naznačují parciální derivace podle času a Δ je standardní Laplacův operátor; pro případ stacionárního magnetického pole degeneruje soustava (5) v jedinou (již zmiňovanou) Laplacovu rovnici ΔH = 0.

Obr. 6: Zkoušení různých tvarů cívek pro elektromagnetické pole s harmonickým buzením

Pro speciální harmonické buzení lze nicméně soustavu (5) převést (viz opět [Val²]) do tvaru jediné formálně stacionární rovnice v komplexním oboru s volným parametrem budicí frekvence a s vhodnými okrajovými podmínkami. Na této myšlence je založena elektromagnetická metoda testování a) i b). Pro normované materiálové vzorky pracuje na tomto principu komerční zařízení z obr. 4 napravo, odkazující k analýze [Fai] a [Wic]; obr. 6 však navíc ukazuje vývoj (ve spolupráci Fakulty stavební a Fakulty elektrotechniky a komunikačních technologií VUT v Brně) originální plně nedestruktivní sondy, použitelné rovněž na realizovaných konstrukcích in situ.

Zhodnocení:

1. Metodu lze navrhnout jako zcela nedestruktivní, příslušné měřicí zařízení je však teprve ve vývoji.
2. Metoda není nákladná, k pořizovací ceně existujícího komerčního zařízení však přistupují náklady na přípravu normových vzorků. U nově vyvíjeného nedestruktivního zařízení na VUT se počítá s patentovou ochranou.
3. Oproti magnetickým měřením lze počítat se zvýšením přesnosti. Srovnatelné hodnoty příslušných materiálových charakteristik cementové matrice a by nicméně byly vážnými argumenty proti použití této metody.
4. Lze počítat se zpřesněním a) oproti magnetickým měřením. Pro zhodnocení nejistot b) není dosud dostatek relevantních informací.

6. Závěr

V tomto článku jsme poukázali na převážně nedestruktivní či málo invazivní metody vyšetřování charakteristik a) a b), ve své podstatě geometrických, které jsou podstatné pro predikci mechanických vlastností vláknobetonu. Jeho krátkodobé i dlouhodobé vlastnosti nicméně ovlivňuje řada dalších faktorů: vedle c), d) a e), které se vesměs vztahují k makroskopické představě o materiálu, rovněž lokální poruchy, například místní koncentrace vláken, způsobená obvykle nedokonalým technologickým postupem. Ve shodě s [Cun] je pak třeba považovat za podstatné studium možného kvazikřehkého lomu vláknobetonu s cílem jeho vyloučení či aspoň maximálního omezení vhodným umístěním drátků (nebo dokonce i jejich promyšlenou orientací, i když zde se naráží na reálné technologické možnosti).

Studium případných postkritických stavů (ve smyslu inicializace a šíření trhlin) představuje samostatný výzkumný problém, výpočtově zvládnutelný pomocí kohezních prvků pro modelování předem odhadnutelných trhlin, případně i vhodným rozšířením běžné metody konečných prvků (X-FEM čili „eXtended Finite Element Method“ apod.). Závažný problém pak ovšem (se zvýrazňováním nelineárního charakteru úlohy a uplatňováním nevratných fyzikálních dějů) představuje návrh a identifikace potřebných efektivních materiálových charakteristik.

Vztah mezi a), b) a dalšími měřitelnými charakteristikami na jedné straně a chováním zatížené konstrukce na bázi vláknobetonu na druhé straně představuje (bez ohledu na normotvorné snahy podle [Bou] či [Han]) dodnes plně nevyřešený problém. Jeho řádné studium (s ohledem na přítomnost řady fyzikálních i chemických procesů, jež nelze zohlednit v relativně jednoduchém matematickém modelu) musí být nutně založeno na součinnosti experimentálních prací v různých typech laboratoří s vývojem původních nástrojů pro výpočtové simulace.

Poděkování

Tento článek vznikl v rámci projektu LO1408 AdMaS UP – Advanced Materials, Structures and Technologies, podporovaného MŠMT ČR v rámci Národního programu udržitelnosti I.

Použitá literatura

• [Bou] Boulmezaoud, T. Z., El Rhabi, M. On time-harmonic Maxwell’s equations in Lipschitz and multiply-connected domains of R3. Monografías del Seminario Matemático García de Galdeano 27 (2003), p. 127–134.
• [Cio] Ciorănescu, D., Donato, P. An Introduction to Homogenization. Oxford University, 1999.
• [Cun] Cunha, V. M. C. F, Barros, J. A. O., Sena-Cruz, J. M. An integrated approach for modelling the tensile behaviour of steel fibre reinforced self-compacting concrete. Cement and Concrete Research 41 (2011), 64–76.
• [Fai] Faifer, M., Ferrara, L., Ottoboni, R., Toscani, S. Low frequency electrical and magnetic methods for non-destructive analysis of fiber dispersion in fiber reinforced cementitious composites: an overview. Sensors 13 (2013), 1300–1318.
• [Flá] Fládr, J., Hejnic, F., Bílý, P. Ověření homogenity ztvrdlého drátkobetonu pomocí obrazové analýzy. Beton 16/2 (2016), 18–21.
• [Gaw¹] Gawin, D., Pesavento, F. An overview of modeling cement based materials at elevated temperatures with mechanics of multi-phase porous media. Fire Technology 48 (2012), 753–793.
• [Gaw²] Gawin, D., Pesavento, F., Schrefler, A. Simulation of damage–permeability coupling in hygro-thermo-mechanical analysis of concrete at high temperature. Communications in Numerical Methods and Engineering 18 (2002), 113–119.
• [Gio] Giordano, S. Effective medium theory for dielectric ellipsoids. Journal of Electrostatics 58 (2003), 59–76.
• [Han] Hanzlová, H., Veselý, V., Vodička, J. Nové české normy pro vláknobeton. Beton 16/2 (2016), 3–6.
• [Hob¹] Hobst, L., Anton, O, Vodička, J., Ščučka, J. Homogeneity detection of fibre-concrete structures by using radiographic technique. Nondestructive Testing of Materials and Structures – Proceedings of International Conference in Istanbul (2012), 323–328. RILEM Bookseries 6, Springer, Berlin, 2013.
• [Hob²] Hobst, L., Bílek, P., Anton, O., Zikmund, T. Stanovení přesné polohy drátků v kalibračních vzorcích drátkobetonu počítačovou tomografií. Zkoušení a jakost ve stavebnictví 2013 – sborník příspěvků konference v Brně (2013), 33–42. VUT v Brně, 2013.
• [Hob³] Hobst, L., Bílek, P., Láník, J., Vodička, J. Předběžné měření koncentrace drátků v drátkobetonových segmentech ostění tunelu. Zkoušení a jakost ve stavebnictví 2014 – sborník příspěvků konference v Brně (2014), 93–101. VUT v Brně, 2014.
• [Hob⁴] Hobst, L., Komárková, T., Vala, J. Electromagnetic approach to nondestructive testing of fibre concrete. International Journal of Materials 2 (2015), 35–39.
• [Kär] Kärkkäinen, S., Vedel Jensen E. B. Estimation of fibre orientation from digital images. Image Analysis and Stereology 20 (2001), 199–202.
• [Ngu] Nguetseng, G., Svanstedt, N. ϭ-convergence. Banach Journal of Mathematical Analysis 5 (2011), 101–135.
• [Pos] Pospíšil, T. On statistical description of random structures. Engineering Mechanics 17 (2010), 383–392.
• [Pou] Pouillon, S. Drátkobeton pro konstrukční účely. Beton 16/5 (2016), 55–59.
• [Rud] Rudraraju, S. S., Garikipati, K., Waas, M., Bednarcyk, B. A. On the Theory and Numerical Simulation of Cohesive Crack Propagation with Application to Fiber-Reinforced Composites. Research report, NASA/TP-2013-217431, Hanover (MD, USA), 2013.
• [Sla] Slabý, O., Veselý, V., Smiřinský, S., Vašková, J. Pingpongový stůl z tenkostěnných prvků z UHPC. Beton 16/5 (2016), 60–64.
• [Val¹] Vala, J. Computational approaches to some inverse problems from engineering practice. 17^th PANM (Programs and Algorithms of Numerical Mathematics) in Dolní Maxov (Czech Republic 2014), 215–230. Institute of Mathematics AS CR, Prague, 2015.
• [Val²] Vala, J. Structure identification of metal fibre reinforced composites. 20^th Algoritmy (Conference on Scientific Computing) in Podbanské (Slovak Republic, 2016), 244–253. Slovak Technical University, Bratislava, 2016.
• [Val³] Vala, J., Hobst, L., Kozák, V. Detection of metal fibres composites based on signal and image processing approaches. WSEAS Transactions on Applied and Theoretical Mechanics 10 (2015), 39–46.
• [Val⁴] Vala, J., Horák, M. Nondestructive identification of engineering properties of metal fibre composites, 10^th ICNAAM (International Conference of Numerical Analysis and Applied Mathematics) in Kos (Greece, 2014), AIP (American Institute of Physics) Conference Proceedings 1479, 2012, 2208–2211.
• [Vin] Vinkler, M., Vítek, J. L. Vysychání a smršťování betonu. Beton 16/2 (2016), 40–45.
• [Vít] Vítek, J. L., Smiřinský, S., Veselý, P., Veselý, V. Rozptyl parametrů drátkobetonu ve vazbě na způsob jeho výroby. Fibre Concrete 2016 – sborník konference v Praze. ČVUT, Praha, 2016.
• [Wei] Weidemann, G., Stadie, R., Hillemeier, B. Computer tomography study of fibre reinforced autoclaved aerated concrete. Materials Testing 50 (2008), 278–285.
• [Wic] Wichmann, H.-J., Budelman, H., Holst A. Determination of steel fiber dosage and steel fiber orientation in concrete. Nondestructive Testing of Materials and Structures – Proceedings of International Conference in Istanbul (2012), 239–245. RILEM Bookseries 6, Springer, Berlin, 2013.
• [BSI] BS EN 14721: Test method for metallic fibre concrete – Measuring the fibre content in fresh and hardened concrete. BSI, 2005, 2007.
• [Č50] ČSN P 732350: Vláknobeton – Specifikace, vlastnosti, výroba a shoda. Předběžná česká technická norma. ÚNMZ, Praha, 2015.
• [Č51] ČSN P 732351: Vláknobeton – Zkoušení čerstvého vláknobetonu. Předběžná česká technická norma. ÚNMZ, Praha, 2015.
• [Č52] ČSN P 732352: Vláknobeton – Zkoušení ztvrdlého vláknobetonu. Předběžná česká technická norma. ÚNMZ, Praha, 2015.
• [Daf] DafStb Richtlinie 2012-11: Stahlfaserbeton. Deutscher Ausschuss für Stahlbeton, Berlin, 2012.
• [DIN] DIN EN 1992-1-1/NA: Design of concrete structures – Part 1.1: General rules and rules for buildings. CEN, Brussels, 2004.