Dynamické a statické moduly pružnosti betonu
U betonu zabudovaného v konstrukci je obtížné stanovit hodnotu statického modulu pružnosti. Jednou z možností je měření modulu dynamického a následný přepočet na modul statický. Příspěvek se zabývá vzájemnými poměry mezi statickým a dynamickým modulem včetně praktických příkladů stanovení zmenšovacího součinitele.
1. Úvod
Stále častěji je při výstavbě železobetonových konstrukcí a mostů předepisována požadovaná hodnota statického modulu pružnosti v tlaku betonu. Vyhodnocení zkoušek modulu pružnosti je však obtížné, neboť na rozdíl od pevnosti betonu v tlaku po modul pružnosti v podstatě neexistují v současných českých normách kritéria pro posouzení shody. Většina požadavků na modul pružnosti se opírá o směrné průměrné hodnoty modulů pružnosti z Eurokódu 2 (nikoliv charakteristické!), které platí pro běžné silikátové kamenivo. Pokud by se na vyhodnocení charakteristické hodnoty modulu pružnosti uplatnila podobná kritéria pro pevnost betonu v tlaku, pak by musel být kromě průměrné hodnoty zohledněn ještě variační součinitel (rovnoměrnost betonu) a při zkouškách in situ s kalibrací na vývrtech by muselo být uplatněno kritérium z ČSN EN 13791, které pro charakteristickou hodnotu pevnosti in situ požaduje splnění pouze 85 % charakteristické hodnoty na normových tělesech – a to by mělo být uplatněno i pro modul pružnosti.
Modul pružnosti betonu je dále ovlivněn řadou činitelů, např. složením, zejména druhem hrubého kameniva [1], ošetřováním [3], provzdušněním [4] apod. Hodnoty statického modulu pružnosti se obvykle zjišťují na předem vyrobených zkušebních tělesech ve tvaru hranolu nebo válce. Řada prací se zabývala porovnáním hodnot modulů na takto rozdílných tělesech – viz např. [5]. Pokud je beton již zabudován do konstrukce, je třeba provést odběr zkušebních těles jádrovým vrtáním a modul stanovit na vývrtech [6], což však představuje značný zásah do konstrukce, který není vždy žádoucí nebo dokonce možný. Při tom existuje poměrně jednoduché řešení – stanovení dynamického modulu pružnosti betonu z ultrazvukového měření in situ a následný přepočet na modul statický [2]. Cílem příspěvku je na příkladech ukázat, jaký existuje vzájemný poměr mezi dynamickým a statickým modulem pružnosti a čím je ovlivněn.
2. Stanovení statického modulu pružnosti betonu přepočtem z modulu dynamického
2.1. Metodiky pro stanovení modulu pružnosti
Pro stanovení dynamických modulů pružnosti jsou využívány metody ultrazvuková a rezonanční, popsané v ČSN 73 1371, ČSN EN 12504-4 a ČSN 73 1372. Hodnotu dynamického modulu pružnosti v tlaku a tahu Edyn,U v N/mm2 vypočteme z naměřené rychlosti šíření UZ impulsů jako:
kde je
- D
- – objemová hmotnost materiálu, v kg/m3;
- vL
- – rychlost šíření ultrazvukového impulsu, v m/s;
- k
- – koeficient rozměrnosti prostředí, bez rozměru.
Dynamický modul pružnosti z rezonančních frekvencí v N/mm2 můžeme stanovit dvěma způsoby; podélného jako Edyn,FL a příčného jako Edyn,FF.
kde je
- fL , ff
- – vlastní frekvence podélného a příčného kmitání v kHz;
- L
- – délka vzorku v m;
- D
- – objemová hmotnost betonu, v kg/m3;
- i
- – poloměr setrvačnosti průřezu;
- c
- – hodnota závislá na poměru i/L a na Poissonově koef. μbr.
Statický modul pružnosti v tlaku se podle ČSN ISO 6784 zjišťuje z deformací, které nastávají při známém zatížení:
kde je
- σa
- – horní zatěžovací napětí v N/mm2;
- σb
- – základní zatěžovací napětí v N/mm2;
- Δε
- – průměrná změna poměrného přetvoření mezi horním a základním napětím.
2.2. Vzájemný poměr mezi statickými a dynamickými moduly podle ČSN 73 2011
Hodnoty statických modulů pružnosti vycházejí vždy nižší než hodnoty modulů dynamických. Při znalosti vzájemného poměru mezi hodnotami dynamických a statických modulů pružnosti bychom v daleko větší míře mohli využívat právě nedestruktivních dynamických metod. Znovu vydaná norma ČSN 73 2011 z roku 2012 obsahuje orientační hodnoty zmenšovacích součinitelů κu (ultrazvuk) a κr (rezonance) – viz Tabulku 1.
| Zmenš. souč. | C 8/10 | C12/15 | C16/20 | C25/30 | C30/37 | C35/45 | C40/50 | C45/55 |
|---|---|---|---|---|---|---|---|---|
| κu | 0,62 | 0,71 | 0,76 | 0,81 | 0,83 | 0,86 | 0,88 | 0,90 |
| κr | 0,81 | 0,86 | 0,88 | 0,90 | 0,91 | 0,93 | 0,94 | 0,95 |
Je však zapotřebí si uvědomit, že autoři nového vydání normy pouze převzali hodnoty uváděné ve starším vydání z osmdesátých let 20. století.
Hodnoty uvedené Tabulce 1 byly stanoveny před 30 lety pro tradiční betony vyráběné odlišným způsobem než dnes. Skutečné hodnoty zmenšovacích součinitelů pro moderní betony vycházejí nižší, ovšem není problém je pro konkrétní beton stanovit. Kromě pevnostní třídy betonu je poměr mezi statickými a dynamickými moduly pružnosti ovlivněn dalšími vlivy, z nichž některé si dále ukážeme na příkladech.
2.3. Vliv doby zrání na vztah mezi statickými a dynamickými moduly pružnosti
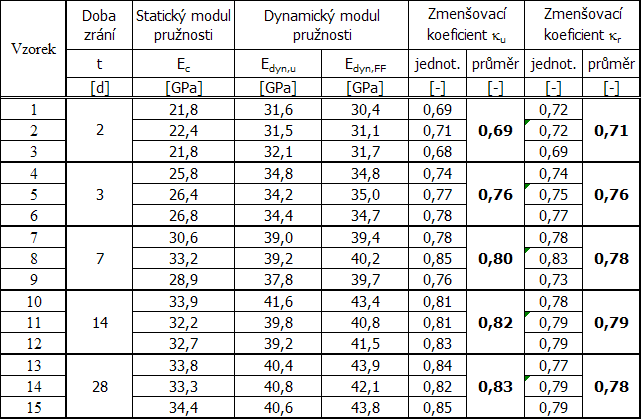
Jedním z vlivů na poměr mezi statickými a dynamickými moduly pružnosti je doba zrání betonu. Tato problematika částečně souvisí s nárůstem pevnosti. Typickým příkladem je mostní beton pevnostní třídy C 30/37 s hrubým kamenivem Olbramovice. V Tabulce 2 a na Obrázku 1 jsou uvedeny a znázorněny výsledky zkoušek statického modulu pružnosti Ec a dynamických modulů pružnosti Edyn,U (z ultrazvuku) a Edyn,FF (z příčné rezonanční frekvence). Všechny zkoušky byly prováděny na hranolech o rozměrech 100×100×400 mm ve stavu přirozeně vlhkém. Pro jednotlivé etapy zkoušení 2, 3, 7, 14 a 28 dnů od betonáže byly vypočteny jednotlivé a průměrné hodnoty zmenšovacích součinitelů pro přepočet dynamických modulů ultrazvukových (κu) a rezonančních (κr) na moduly statické.
Jak je patrné z Tabulky 2, se vzrůstající dobou zrání roste hodnota zmenšovacích koeficientů κu, κr, tedy dochází ke snižování rozdílu mezi dynamickými a statickými moduly pružnosti. Trend je poměrně plynulý. Po 28 dnech zrání dosahuje statický modul pružnosti 83 % hodnoty dynamického ultrazvukového modulu pružnosti, což přesně odpovídá hodnotě normového koeficientu. Naopak u rezonanční metody je skutečný koeficient (κr = 0,78) výrazně nižší než hodnota normová.
Tabulka 2.: Hodnoty zmenšovacích koeficientů pro přepočet dynamických modulů ultrazvukových (κu)
a rezonančních (κr) na moduly statické pro beton pevnostní třídy C 30/37 v různém stáří
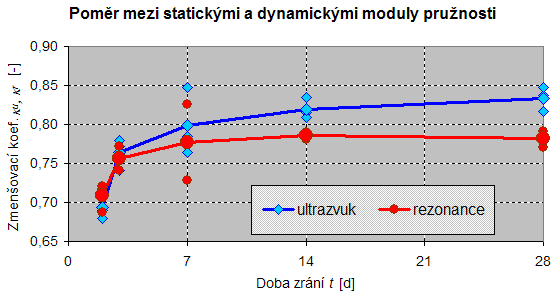
Obrázek 1.: Vliv doby zrání betonu na poměr mezi statickým a dynamickými moduly pružnosti betonu C 30/37
2.4. Vliv použitého hrubého kameniva na vztah mezi statickými a dynamickými moduly pružnosti
| Označení | Žula | Droba | Čedič |
|---|---|---|---|
| Vodní souč. | 0,33 | 0,33 | 0,33 |
| CEM I 42,5 R | 420 | 420 | 420 |
| Metakaolin | 35 | 35 | 35 |
| Voda | 150 | 150 | 150 |
| Superplastif. | 7,5 | 7,5 | 7,5 |
| Písek 0/4 | 625 | 625 | 625 |
| Drť 4/8 | 245 | 245 | 275 |
| Drť 8/16 | 975 | 975 | 1097 |
Druh hrubého kameniva je zcela zásadní jak pro výslednou hodnotu modulu pružnosti betonu, tak i pro vzájemný poměr mezi hodnotami modulů dynamických a statických. Vliv použitého hrubého kameniva na hodnoty zmenšovacích součinitelů κu a κr je ukázán na příkladu tří druhů vysokopevného betonu, lišících se pouze druhem hrubého kameniva – žuly, droby a čediče, jehož složení je uvedeno v Tabulce 3.
Výsledky zkoušek betonu po 1 a 28 dnech zrání jsou uvedeny v Tabulce 4 až 6 a graficky znázorněny na Obrázku 3 až 5. Pevnost v tlaku byla stanovena na krychlích o hraně 150 mm, dynamické i statické moduly pružnosti byly zjišťovány na hranolech s rozměry 100×100×400 mm. Beton byl zkoušen ve stavu nasyceném vodou.
Tabulka 4.: Výsledné průměrné hodnoty statického modulu pružnosti
pevnosti v tlaku betonu po 1 a 28 dnech zrání

Tabulka 5.: Hodnoty dynamického modul Edyn,U a součinitelů κu

Tabulka 6.: Hodnoty dynamického modul Edyn,FF a součinitelů κr

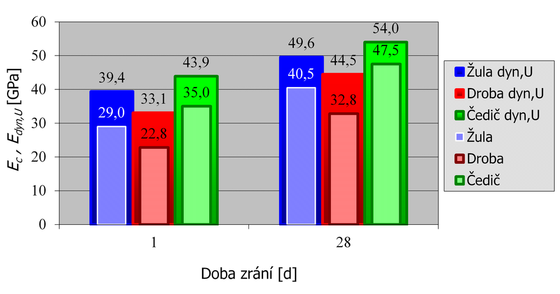
Obrázek 2.: Statické (nižší) a dynamické (vyšší) moduly pružnosti betonu C 70/85 s různými druhy hrubého kameniva
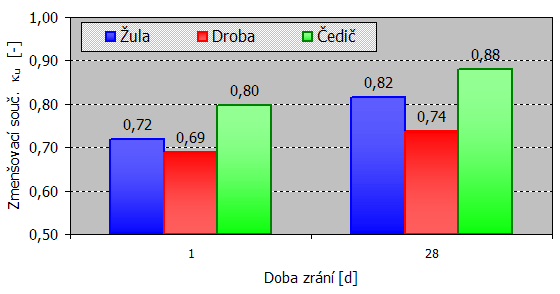
Obrázek 3.: Hodnoty zmenšovacího součinitele κu (ultrazvuk)
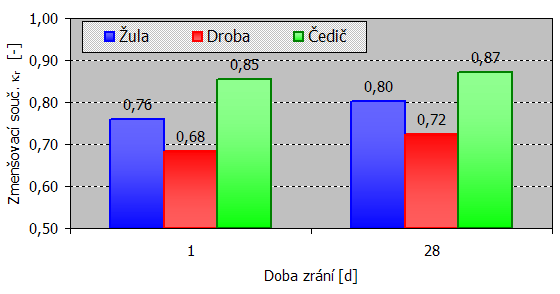
Obrázek 4.: Hodnoty zmenšovacího součinitele κr (rezonance) pro betony s různým kamenivem po 1 a 28 dnech zrání
Vliv typu kameniva na modul pružnosti je velmi výrazný. Při zachování parametrů směsi (vodního součinitele, dávky superplastifikátoru, objemu hrubého kameniva), vykazuje beton s čedičem po 1 dni zrání takovou hodnotu modulu pružnosti, jakou beton s drobou nedosáhl ani po 28 dnech. Proti tomu vliv kameniva na pevnost v tlaku tak výrazný nebyl, neboť ve všech případech se jednalo o kamenivo s vysokou pevností v tlaku. Betony se žulou a drobou byly z hlediska pevnosti v tlaku prakticky srovnatelné, vyšších pevností bylo dosaženo pouze u betonu s čedičem, a to až po 28 dnech zrání.
Výrazně rozdílné byly rovněž hodnoty zmenšovacích součinitelů κu a κr pro přepočet dynamických modulů pružnosti z ultrazvukových a rezonančních měření na moduly statické. Např. pro ultrazvukové měření vychází nejnižší součinitel u betonu s drobou: κu = 0,68 po 1 dnu a κu = 0,72 po 28 dnech zrání. Proti tomu u betonu s čedičem byly součinitele výrazně vyšší: κu = 0,80 po 1 dnu a κu = 0,88 po 28 dnech. Součinitele u betonu s běžným žulovým kamenivem vycházely průměrné, např. po 28 dnech zrání κu = 0,82. U rezonanční metody byly výsledky obdobné.
Porovnáním hodnot součinitelů κu, κr zjištěné měřením s hodnotami normovými (Tabulka 1) zjistíme, že stejné hodnoty těchto součinitelů byly dříve dosahovány u betonů výrazně nižších pevnostních tříd.
2.5. Vliv vodního součinitele na vztah mezi statickými a dynamickými moduly pružnosti
Posledním příkladem je zhodnocení vlivu vodního součinitele na poměr mezi dynamickými a statickými moduly pružnosti. Z prakticky identických surovin, s hrubým kamenivem žulou, byly namíchány tři druhy betonu lišící se vodním součinitelem w = 0,33, 0,38 a 0,43. Navrhovaná pevnostní třída betonu s nejvyšší hodnotou vodního součinitele byla C 50/60, u dalších receptur se předpokládal nárůst pevností vždy minimálně o třídu. Výsledky zkoušek modulů pružnosti a pevnosti v tlaku betonů s rozdílným vodním součinitelem včetně hodnot zmenšovacích součinitelů κu, κr jsou uvedeny v Tabulce 7. Beton byl opět uložen ve vodě, pevnost v tlaku byla zkoušena na krychlích a dynamické i statické moduly pružnosti na hranolech o rozměrech 100×100×400 mm.
Tabulka 7.: Vliv vodního součinitele na hodnoty modulů pružnosti a zmenšovacích
součinitelů κu, κr
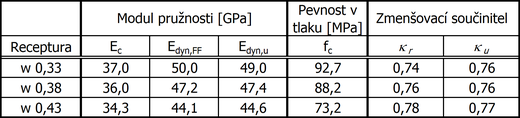
Na rozdíl od výrazného vlivu použitého druhu hrubého kameniva nemá vodní součinitel prakticky žádný vliv na hodnoty zmenšovacích součinitelů κu, κr. Jinak řečeno, se snižováním vodního součinitele narůstají statické i dynamické moduly pružnosti ve stejném poměru.
3. Závěr
Cílem článku bylo ukázat možnosti stanovení statického modulu pružnosti z dynamických měření. Zvlášť výhodné je použití ultrazvuku, neboť na rozdíl od rezonanční metody lze tuto metodu snadno aplikovat in situ. Pokud se pro přepočet použijí koeficienty z normy ČSN 73 2011, pak statické moduly pružnosti vyjdou vyšší, než odpovídá realitě. Pro jakýkoliv beton konkrétního složení lze získat přesné hodnoty zmenšovacích součinitelů, pokud jsou k dispozici zkušební tělesa předem vyrobená nebo dodatečně odebraná, na nichž lze provést stanovení jak dynamického, tak i statického modulu pružnosti betonu. V praxi je měření tím přesnější, čím lépe se podaří dodržet shodné podmínky měření – beton stejného složení, stáří a vlhkosti.
Poděkování
Tento příspěvek vznikl za podpory projektu specifického vysokoškolského výzkumu FAST-J-12-1809 s názvem „Vliv zastavení hydratace betonu v různých stádiích zrání na jeho charakteristiky“.
Literatura
- [1] CIKRLE, P.; BÍLEK, V. Modul pružnosti vysokopevných betonů různého složení. Beton TKS. 2010. 2010(5). p. 40–44. ISSN 1213-3116.
- [2] CIKRLE, P.; KOCÁB, D.; POSPÍCHAL, O. Zkoušení betonu ultrazvukovou impulsovou metodou. Beton TKS. 2013. 13(3). p. 74–79. ISSN 1213-3116.
- [3] KOCÁB, D.; CIKRLE, P. Influence of Water Curing Concrete on the Dynamic Modulus of Elasticity of Concrete for Bridge Constructions. In Non-Destructive Testing in Engineering Practice. Brno, CERM. 2010. p. 141–146. ISBN 978-80-7204-723-9.
- [4] KOCÁB, D.; CIKRLE, P.; ADÁMEK, J.; POSPÍCHAL, O. Vliv provzdušnění na modul pružnosti mostního betonu. In Sborník příspěvků 9. konference TECHNOLOGIE BETONU 2010. Pardubice, ČBS Servis, s.r.o. 2010. p. 16–21. ISBN 978-80-87158-23-4.
- [5] Petr Huňka, Jiří Kolísko, Stanislav Řeháček, Miroslav Vokáč Zkušební a technologické vlivy na modul pružnosti betonu – rekapitulace. Beton TKS. 2012. 12(4). p. 62–67. ISSN 1213-3116.
- [6] POSPÍCHAL, O.; KOCÁB, D.; CIKRLE, P.; DANĚK, P. Stanovení modulu pružnosti jádrových vývrtů betonu použitého pro hodnocení vlivu délky ošetřování na kvalitu betonu. In ZKOUŠENÍ A JAKOST VE STAVEBNICTVÍ 2012. Brno, Vysoké učení technické v Brně. 2012. p. 63–68. ISBN 978-80-214-4578-9.
The concrete built in the structure is difficult to determine the static modulus of elasticity. One possibility is to measure the dynamic modulus of elasticity and subsequent conversion to static modulus of elasticity. This paper deals with mutual relationships between static and dynamic modulus of elasticity including practical examples of the determination of reduction factor.