Modelování fyzikálních jevů 1 - Odpar z vodní hladiny
Článek se zabývá popisem a řešením fyzikálních jevů uplatňujících se při odparu z vodní hladiny. Aktuálnost tématu je dána množstvím budovaných krytých bazénů a wellness center v současnosti. Pro návrh systémů vzduchotechniky obsluhujících tyto prostory je nutné znát návrhové parametry ve vnitřním prostoru, zejména teplotu bazénové vody, požadované teploty a vlhkosti vzduchu. Článek ukazuje na zásadní význam těchto parametrů pro odpar vody z hladiny.
Úvod
Při navrhování vzduchotechnických zařízení obsluhující prostory bazénů, krytých vodních ploch a wellness technologií je nutné zjišťovat hmotnostní toky odpařující se vody a rovněž toky tepla z mokrých povrchů nebo z vodních hladin odkrytých nádrží. Odpařování zahrnuje přenos tepla i vlhkosti (hmoty), přičemž oba procesy současně ovlivňují termodynamický stav vzduchu nad těmito povrchy. Pro tyto případy byl na ústavu TZB Fakulty stavební VUT v Brně v rámci výzkumu modelování fyzikálních jevů vytvořen nový modul pro software TERUNA nazvaný „bazény“. Modul se skládá z výpočtu odparu z hladiny, samostatným řešením a návrhem skladby VZT jednotky včetně termodynamických úprav vzduchu a prvkem pro snadné nalezení optimální varianty návrhu z hlediska energetických spotřeb daného VZT zařízení. Tento článek představuje 1. část modulu a to výpočet odparu z vodní hladiny. V následujícím článku „Modelování fyzikálních jevů 2“ budou řešeny skladby, úpravy a fyzikální děje probíhající v samotné vzduchotechnické jednotce.
Teorie přenosu vlhkosti
Přenos vlhkosti se děje ve většině případů difuzí vodní páry z vodní hladiny do vzduchu, ale jsou případy, kdy může docházet k obrácenému gradientu difuze vodní páry. Směr hmotnostního toku páry určují jednotlivé psychrometrické a fyzikální veličiny vody a vzduchu. Hustotu hmotnostního toku tekutin při jejich stacionární difuzi mezi místy s různou koncentrací (platí pro izotermní děje), případně různým parciálním tlakem (platí obecně) vyjadřuje Fickův zákon:
Qm = −Dc ‧ δc δn = −DD ‧ δρ δn (1.1) [kg/m2s]
kde
- c
- – koncentrace difundující látky [kg/m7]
- n
- – délka směru normály k izobarám nebo čárám s konkrétní koncentrací [m]
- Dc
- – součinitel difuze vztahující se k rozdílu koncentrací [m/s]
- DD
- – tlakový součinitel difuze vztahující se k rozdílu parciálních tlaků [kg/msPa]
Vzhledem k faktu, že koncentrace se shodují s hustotou (c Ξ ρ), po vyjádření ρ ze stavové rovnice ideálního plynu a dosazení do vztahu Fickova zákona (1.1) platí Dc = r ‧ T ‧ DD. Vzhledem k tomu, že hodnota Dc je pro vzduch i vodní páru shodná, lze pro poměr DDP = rv / rp = 0,622 určit vztah:
Dc = 2,194 pb ‧ T 1,8 2731,8 = 90,395 ‧ 10−5 ‧ T 1,8 pb (1.2) [m2/s]
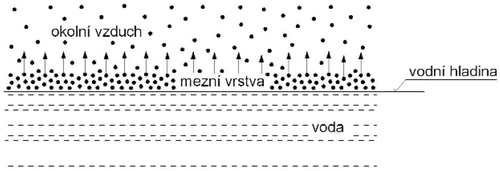
Obr.1 Znázornění principu odpařované vody
Fickův zákon platí pro oboustrannou difuzi, která však obvykle nenastává. Vodní pára může difundovat z vodní hladiny do vzduchu bez překážek, vzduch do vodní hladiny difundovat nemůže. Tj. molekuly vodní páry difundují z hladiny do vzduchu a současně i molekuly vzduchu difundují směrem k hladině. Molekuly vzduchu se však dostanou pouze na povrch nepřestupné hladiny, kde se shlukují a nasycují vodní párou a konvekčním pohybem se vracejí zpět. Pohybem vodní páry se zvyšuje tok jejich molekul, které difundují ve vzduchu. Hmotnostní tok vodní páry je tak při jednostranné difuzi větší než při oboustranné. Korekce toku odpařující se vlhkosti se označuje jako Stefanova korekce na jednostrannou difuzi.
Teorie přestupu tepla a hmoty mezi vodní hladinou a vzduchem
Prostup citelného tepla konvekcí z vodní hladiny s plochou Sh [m2] a teplotou th [°C] do vzduchu s teplotou tv [°C] popisuje vztah:
Qc=α ‧ Sh ‧ (th−tv) (1.3) [W]
kde
- α
- – součinitel přestupu tepla mezi vodní hladinou a vzduchem
Konvektivní tok vodní páry z hladiny do vzduchu popisují rovnice:
mp = βp ‧ Δpp ‧ Sh = βp ‧ (ph“−pp) ‧ Sh (1.4) [kg/s]
mp = βx ‧Δx ‧ Sh = βx ‧ (xh“−x) ‧ Sh (1.5) [kg/s]
kde
- βp
- – součinitel přenosu vlhkosti vztahující se k rozdílům parciálních tlaků syté vodní páry těsně nad hladinou a vodní páry v okolním vzduchu [kg/m2.Pa]
- βx
- – součinitel přenosu vlhkosti vztahující se k rozdílu specifických vlhkostí nasyceného vzduchu těsně nad hladinou (při teplotě hladiny a vzduchu v okolí) [kg/m2.s]
- pph“
- – tlak syté vodní páry [Pa]
- xh“
- – měrná vlhkost [kg/kg] v okolním vzduchu při teplotě tv [°C]
Aplikace teorie a realizace výpočtu
Zásadním úkolem při praktickém výpočtu je určení součinitele přestupu tepla, součinitele přestupu vázaného tepla v mezní vrstvě nad hladinou a také psychrometrické a energetické veličiny vzduchu a vody v různých vrstvách. Všechny tyto veličiny jsou závislé na základních okrajových podmínkách výpočtu. Tyto jsou:
- pro vzduch
- teplota vnitřního vzduchu [°C]
- relativní vlhkost vnitřního vzduchu [%]
- rychlost proudění vzduchu nad hladinou [m/s]
- pro vodu
- teplota vody [°C]
Z uvedených okrajových podmínek je možné výpočtem určit další parametry stavu vzduchu jak v interiéru, tak v mezní vrstvě nad hladinou. Jedná se zejména o:
- pro vzduch
- teplota mokrého teploměru [°C]
- tlaky sytých par v rosném bodu a v bodě mokrého teploměru [Pa]
- měrné vlhkosti [g/kg]
- entalpie [kJ/kg]
- mezní vrstva
- teplota [°C]
- tlak syté páry
- měrná vlhkost
- entalpie vody
- entalpie vzduchu
- součinitel odparu [g/s‧m2]
- součinitel přestupu tepla [W/m2‧K]
Na základě veličin určujících fyzikální podmínky v mezní vrstvě a aplikaci Fickova zákona je možné vypočítat jednotlivé toky tepla a hmotnostní tok vody.
Výpočetní algoritmus je sestaven v programovacím prostředí Borland Delphi 7 jako zvláštní výpočetní modul pro simulační software TERUNA. Zde je možné jednoduchým způsobem simulovat okrajové podmínky výpočtu jak pro vzduch vnitřního prostoru včetně rychlosti proudění vzduchu nad hladinou, tak pro bazénovou vodu.
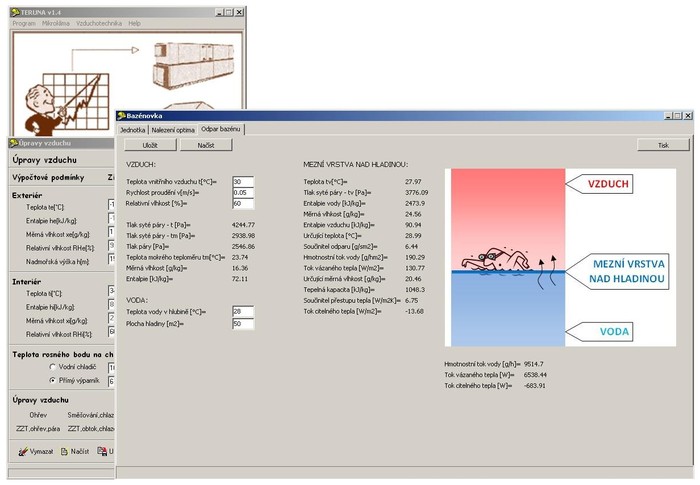
Obr. 2 Ukázka výpočetního modulu „Odpar z vodní hladiny“ v programu TERUNA verze v1.5
Jak je patrné z obrázku jsou ve výstupu výpočtu zobrazeny veškeré fyzikální a psychrometrické veličiny, na kterých výpočet závisí. Jejich kontrolou je možné ověřit správnost výsledků, kterými jsou hodnota odparu z hladiny v kg/h, tok citelného a vázaného tepla ve Wattech.
Výsledky
Počítačové modelování sebou nese možnost rychlého testování vlivů vybraných parametrů na chování sledované soustavy. V případě transferu vlhkosti v bazénové hale jsou zajímavé závislosti:
- množství odpařené vody na teplotě interiéru
- odpařené vody na relativní vlhkosti vzduchu v interiéru
- toku tepla na teplotě interiéru
Zkoumání závislostí představuje jednoduchou citlivostní analýzu, která umožňuje dobře porozumět sledovaným jevům. Řešení formou počítačového modelu je možné právě v programu TERUNA. Výsledky jsou analyzovány níže.
Závislost množství odpařené vody na teplotě interiéru
Pro modelování závislosti odparu na teplotě interiéru byly zvoleny okrajové podmínky tak, aby vyhovovaly fyziologickému vnímání tepelně-vlhkostní mikroklima člověkem v uzavřeném prostoru (teplo, bez dusna). Jako relativní vlhkost interiéru byla zvolena vlhkost 55 %, proudění vzduchu nad hladinou 0,15 m/s. Jedná se o rychlost vzduchu, která vzniká při pohybu plavající osoby. Teplota vody byla zvolena 26 °C a 28 °C. Výsledky jsou zobrazeny v grafu na obr. 3.
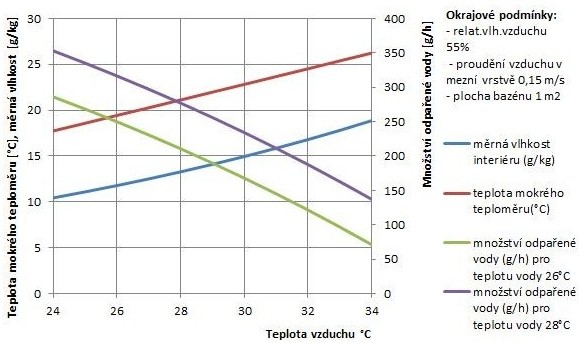
Obr.3 Graf závislosti množství odpařené vody na teplotě interiéru
Z grafu je patrný menší odpar při vyšších teplotách vzduchu, kdy je teplota mokrého teploměru a měrná vlhkost již natolik vysoká, že difuze vodní páry neprobíhá tak intenzivně, jak při nižších teplotách, kdy je vzduch interiéru sušší a pojme větší množství vodní páry. Za předpokladu udržování konstantní relativní vlhkosti je tedy účelné volit vyšší teplotu vzduchu, neboť s rostoucí teplotou se snižuje množství odpařené vody a tím nároky na odvlhčování. Z hlediska teploty vody znamená zvýšení o 2 K nárůst odpařené vody při teplotě vzduchu 31 °C o polovinu.
Závislost odpařené vody na relativní vlhkosti vzduchu v interiéru
V tomto případě byly zvoleny okrajové podmínky tak, aby byla patrná i možná obrácená difuze vodní páry. Teplota bazénové vody byla zvolena jako nejčastěji používaná v praxi u menších rodinných bazénů, tj. 28 °C, proudění vzduchu nad hladinou 0,15 m/s. Výsledky jsou zobrazeny v grafu na obr. 4.
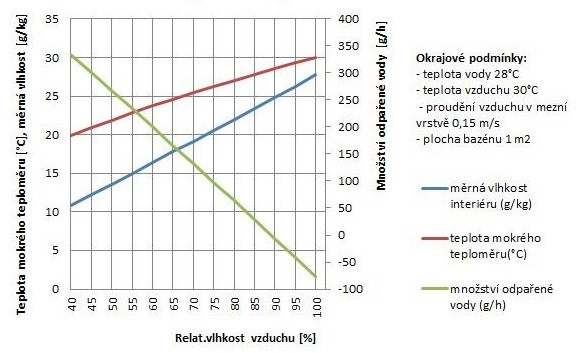
Obr.4 Graf závislosti množství odpařené vody na relativní vlhkosti vzduchu v interiéru
Z grafu je patrný bod, kdy začíná docházet k obrácené difuzi vodní páry. Při zadaných podmínkách se jedná o stav vzduchu 30 °C / 90 %. Při relativní vlhkosti vyšší než 90 % již nedochází k odparu vody z bazénu, ale ke kondenzaci vodní páry v mezní vrstvě u hladiny bazénu.
Závislost toku tepla na teplotě interiéru
Pro tento případ byly zvoleny stejné okrajové podmínky jako při závislosti odparu na teplotě interiéru, teplota bazénové vody 26 °C a 28 °C. Výsledky jsou zobrazeny v grafu na obr. 5.
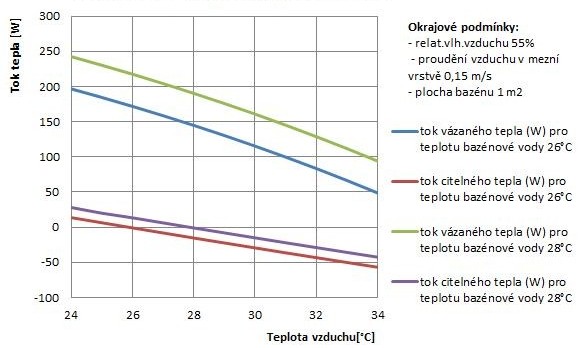
Obr. 5 Graf závislosti toku tepla na teplotě interiéru
Z grafu je patrné, že podle teploty vody a teploty interiéru za daných okrajových podmínek je možné v případě toku citelného tepla očekávat přestup citelného tepla nejen z bazénové vody do vzduchu, ale i obráceně. V případě vázaného tepla toto za daných podmínek neplatí. Opět se ukazuje, že má-li vzduch vyšší měrnou vlhkost (v případě stejné relativní vlhkosti je vzduch teplejší) dochází k menší difuzi vodní páry z bazénu do vzduchu nad hladinou než při teplotách vzduchu nižších.
Závěr
Díky dnešním možnostem počítačového modelování je možné simulovat různé stavy vzduchu a vody a tím zkoumat takové zásadní fyzikální jevy, jako je odpar z vodní hladiny. Článek poukazuje na složitost tohoto fyzikálního problému a nabízí za určitých zjednodušení kompletní řešení pomocí nově vytvořeného výpočetního modulu. Z jednotlivých grafů jsou zřejmé závislosti odparu na jednotlivých fyzikálních a psychrometrických veličinách.
Pochopením dějů probíhajících při odparu vody z hladiny je možné zajistit optimální postup při zpracování technických návrhů daných vzduchotechnických zařízení obsluhující tyto prostory.
Článek vznikl za podpory specifického výzkumu reg. číslo FAST-J-11-30, identifikační číslo 1321.
Literatura
- [1]CHYSKÝ, J., HEMZAL, K. a kol. Technický průvodce větrání a klimatizace. 3. vyd. Praha: ČESKÁ MATICE TECHNICKÁ, 1993. 490 s. ISBN 80-901574-0-8.
- [2]SZÉKYOVÁ, M., FERSTL, K. a NOVÝ, R.. Větrání a klimatizace. 1. české vyd. Bratislava: JAGA, 2006. 359 s. ISBN 80-8076-037-3.
- [3]GEBAUER, G., RUBINOVÁ, O. a HORKÁ, H. Vzduchotechnika. 2. vyd. Brno: ERA, 2007. 262 S. ISBN 978-80-7366-091-8
- [4]BLASINSKI, P. Teplovzdušné větrání wellness sportovního centra, bakalářská práce, VUT v Brně, Fakulta stavební, Ústav technických zařízení budov, Brno, 2010
The article deals with the description and solution of physical phenomena taking place during evaporation of water. The topicality of the theme is given a number of built indoor swimming pool and wellness centers at present. In addressing HVAC systems serving these areas, it is necessary to know the various design parame-ters in the interior including the water temperature as the pool temperature and humidity. The article shows the crucial importance of these parameters in a haze of water from the surface.