Měření tepelných ztrát horkovodů – porovnání jednotlivých metod výpočtu s naměřenými výsledky II.
Článek se věnuje měření teplotního pole v okolí teplárenského potrubí zasypaného v zemi a porovnání jeho tepelných ztrát, získaných z naměřených hodnot, s hodnotami vypočtenými podle různých metodik. Svým obsahem zapadá do několikaletého cyklu článků na téma sdílení tepla v oblasti podzemních potrubních tras z hlediska kvantifikace tepelných ztrát a rozsahu a intenzity teplotního pole, vznikajícího v okolí těchto potrubních sítí.
I. díl článku naleznete ZDE.
Obsah
| 2.3. Zpracování výsledků měření | |
| 2.3.1. Stanovení velikosti tepelného toku, procházejícího izolovanou trubní konstrukcí na základě naměřených hodnot | |
| 2.3.2. Porovnání přesnosti jednotlivých výpočtových metod s naměřenými výsledky | |
| 3. Závěr a shrnutí | |
| 3.1.Výsledky měření | |
| 4. Doporučená Literatura k tématu tepelných jevů v teplárenských sítích |
2.3. Zpracování výsledků měření
Naměřené sady dat, i přes dvojí zálohování (– bylo cílem, aby v každém bodě měření měřila 3 nezávislá měřidla) nejsou v celkovém rozsahu doby měření kontinuální. Z tohoto důvodu nejsou ani výsledky měření zpracovány kontinuálně v časové ose, a vyhodnocení měření zpracovává jednotlivé časové úseky, které se, především z hlediska tématu – hodnocení tepelných ztrát potrubí, ukazují jako zajímavé, a to ať z hlediska své teplotní stability, z hlediska provozních parametrů měřené horkovodní soustavy, z hlediska počasí (teplota vzduchu nad povrchem země), nebo jako hraniční (– ohraničující extrémní provozní stavy). Jedná se např. i o nejchladnější či nejteplejší dny/ týdny v měřeném období.
Na základě naměřených výsledků měření se jako zajímavé, a to především z hlediska naměřené celkové tepelné ztráty (součtu tepelné ztráty přívodního a vratného potrubí), i ve vztahu k ostatním parametrům, jeví následující okamžiky měření (viz Tabulka 2.3.1.):
| Datum a čas | Celková tepelná ztráta přívodního a vratného potrubí q [W/m] | Tepelná ztráta přívodního potrubí qf [W/m] | Tepelná ztráta vratného potrubí qr [W/m] | Teplota vzduchu 2 m nad povrchem země (získána z veřejných zdrojů) TA2 [°C] | Teplota 60 mm pod povrchem země – měř. místo č. 85 t85 [°C] | Teplota přívodního potrubí horkovodu t105 [°C] | Teplota vratného potrubí horkovodu t104 [°C] |
|---|---|---|---|---|---|---|---|
| 27.03.14 18:14 | 19,37 | 13,03 | 6,30 | 12,1 | 12,1 | 74,6 | 44,8 |
| 10.06.14 18:51 | 17,00 | 11,30 | 5,70 | 30,0 | 22,9 | 72,6 | 48,2 |
| 18.11.14 17:33 | 19,08 | 12,64 | 6,44 | 17,4 | 13,6 | 74,8 | 47,6 |
| 26.11.14 20:26 | 23,61 | 16,06 | 7,55 | 2,4 | 5,6 | 88,2 | 52,0 |
| 04.12.14 16:49 | 20,09 | 12,99 | 7,10 | 6,6 | 6,1 | 74,8 | 48,8 |
| 30.12.14 12:05 | 32,80 | 23,10 | 9,70 | −5,5 | 0,5 | 113,4 | 59,3 |
| 05.02.15 16:36 | 27,30 | 18,30 | 9,00 | −0,8 | 0,7 | 94,6 | 54,4 |
| 27.08.15 14:11 | 15,64 | 10,69 | 5,00 | 28,4 | 24,4 | 72,4 | 47,7 |
| 08.09.15 15:17 | 15,90 | 10,80 | 5,10 | 17,8 | 19,2 | 72,4 | 47,9 |
| 13.10.15 14:02 | 22,11 | 15,20 | 6,90 | 4,2 | 9,2 | 88,2 | 53,1 |
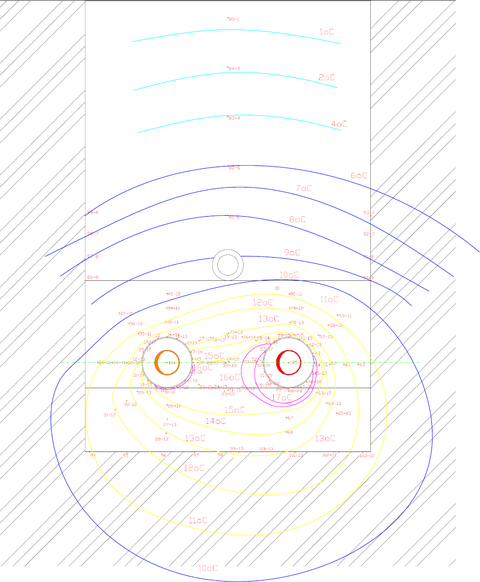
Obrázek 2.3.1. – Umístění jednotlivých izoterm zakreslených na základě měření ze dne 30. prosince 2014 12:05, označení měřících bodů 1 až 105 je na více místech doplněno i hodnotou naměřené teploty ve °C. Hodnoty teplot okolní zeminy budou dále využity pro stanovení tepelné vodivosti zásypové zeminy a k validaci numerického modelu.
Dalším výsledkem měření je získání podkladů pro představu o složení teplotního pole pro konkrétní provozní okamžiky. Na Obrázku 2.3.1. jsou zakresleny izotermy pro typický zimní den, kdy se denní teplota vzduchu na povrchu země pohybuje kolem 0 °C.
2.3.1. Stanovení velikosti tepelného toku, procházejícího izolovanou trubní konstrukcí na základě naměřených hodnot
Stanovení velikosti tepelného toku je provedeno na základě hodnot teplot, naměřených přímo na izolačním plášti přívodního potrubí (měřicí místa č. 41 až 56) a izolačním plášti vratného potrubí (měřicí místa č. 1 až 16) a teplot naměřených na vnější stěně izolovaných medionosných trubek v šachtě Š2, které lze, vzhledem k prokázanému turbulentnímu proudění, a s přihlédnutím k výše uvedeným výpočtů tepelných odporů mezi proudící kapalinou a povrchem ocelové trubky, považovat taktéž i za informativní hodnoty teplot proudu protékající kapaliny.
Vzhledem ke všeobecně známým tepelně-technickým vlastnostem izolační PUR pěny a PEHD krycího pláště je možno, po zprůměrování hodnoty teplot na jednotlivých pláštích, stanovit hodnotu obou tepelných toků
kde t2f a t2r jsou povrchové teploty přívodního a vratného medionosného potrubí, t4fstr je střední teplota na plášti přívodního potrubí, získaná jako aritmetický průměr z hodnot naměřených teplot na měřících místech č. 41–56 a t4rstr je střední teplota na plášti vratného potrubí, získaná jako aritmetický průměr z hodnot naměřených teplot na měřících místech č. 1–16.
∑Rif a ∑Rir jsou součty tepelných odporů izolace a jejího pláště přívodní, resp. vratné trubky.
Na základě téměř konstantní hodnoty tepelného odporu izolačního pláště RC je možno vypočítat teplotu na vnější stěně izolačního mezikruží (o průměru d3) a při znalosti teploty t2f (na povrchu přívodní medionosné trubky) je možno vypočítat teplotu na vnějším povrchu izolační PUR hmoty t3f, a podobně pak z t2r vypočítat i pro potrubí vratné teplotu t3r.
Z těchto hraničních teplot je pak možno zjistit teplotu v jádře izolace, a to na základě určení střední logaritmické teploty v jádře izolační vrstvy pro potrubí přívodní
a pro potrubí vratné
Za použití této hodnoty teploty je vypočtena hodnota tepelné vodivosti λiz(t)start a následně tepelného odporu izolace Riz(t)start , a tím je provedeno první přiblížení ke stanovení správné hodnoty tepelného odporu potrubní izolace Riz(t) , který je v tomto případě funkcí teploty.
Aproximace směřují ke správné hodnotě velmi rychle, tedy např. pro měření provedené dne 24. února 2015 v 17:06, je, při první odhadnuté hodnotě teploty v jádře přívodního potrubí tjfstart = 50,8 °C, už během 2 aprox. kroků, velmi přesně známa teplota v jádře izolace tjf = 37, °C, které odpovídá příslušná hodnota tepelné vodivosti λizf a tedy skutečný tepelný tok qf. Identicky je postupováno i u potrubí vratného tak, aby byl s vysokou přesností určen tepelný tok procházející izolační konstrukcí potrubí.
Výsledkem každé z výpočtových metod pro jednotlivé provozní parametry – tedy především pro kombinace teploty přívodní a vratné vody, spolu s teplotou vnějšího povrchu, je celková tepelná ztráta jednotlivých potrubí a celé dvojice.
2.3.2. Porovnání přesnosti jednotlivých výpočtových metod s naměřenými výsledky
Jedním z cílů provedeného měření je ověření stávajících postupů výpočtu tepelných ztrát vzhledem k možnosti jejich aplikace na současně používané izolační konstrukce potrubí. Jednotlivé analytické metody pro určení tepelné ztráty potrubí zasypaného v zemi, byly podrobně popsány v předcházejících článcích tohoto cyklu, např. zde
http://energetika.tzb-info.cz/12846-analyza-termodynamickych-jevu-v-potrubnich-sitich
Ze získaných hodnot je možno, po srovnání tepelné ztráty vypočtené na základě naměřených teplot s výpočtem dle jednotlivých normalizovaných postupů dovodit, že výpočtová metoda dle ČSN EN 13 941 A1 je vhodná ve středoevropských podmínkách především pro posuzování celoročních ztrát potrubních tras každého roku. Základním problémem pro výpočet podle této normy je zadání teploty okolní, teplovodem/horkovodem tepelně neovlivněné rostlé zeminy, jejíž zjištění v konkrétním okamžiku bývá obtížné a předpokládá práci s dalším výpočtovým aparátem či samostatné určení této teploty měřením. Bez tohoto upřesňujícího výpočtu či měření lze s dostatečnou spolehlivostí pracovat s průměrnou roční teplotou pro konkrétní hloubku potrubí. Avšak i v případě modifikace této normalizované metody tak, že za hodnotu teploty neporušené zeminy vždy dosadíme vypočtenou konkrétní hodnotu teploty okolní zeminy, dosahuje průměrná chyba výpočtu za celé měřené období, ve srovnání s tepelnou ztrátou vypočtenou na základě naměřených hodnot, průměrné výše 8,75 %.
Překvapením jsou výsledky srovnávání naměřených hodnot s poměrně velmi jednoduchým výpočtem tepelné ztráty dle ČSN EN ISO 12 241. Odchylka mezi tepelnou ztrátou získanou z naměřených hodnot a výpočtem dle této normy byla po většinu doby měření menší, než v případě výpočtu dle specializované normy ČSN EN 13 941 a vypočtené odchylky hodnot tepelné ztráty potrubní dvojice se od měření, ve svých maximech, minimech i v průměru, blížily spíše odchylkám, jaké vykazoval očekávatelně poměrně přesný výpočet na základě metodiky výpočtu na základě teorie energetického zdroje i propadu, dle literatury [13].
Výpočet tepelné ztráty za použití tvarového faktoru se ukázal jako nejméně přesný, jak je patrno z přiložených grafů průběhu tepelné ztráty.
Je však nutno vzít v úvahu, že veškeré výsledky mohou být ovlivněny možnou nepřesností měření tak, jak je uvedeno v části 2.2.3.
3. Závěr a shrnutí
3.1.Výsledky měření
Výsledky uvedeného měření je možno, vzhledem k šíři řešeného tématu, rozdělit do tří okruhů:
1/ Na základě 4 aplikovaných výpočtových metod pro určení tepelných ztrát potrubí umístěných v zemním zásypu, založených na analytickém přístupu, lze z předložených výsledků konstatovat, že každá z používaných metod vykazuje rozdílnou míru shody ve vztahu k naměřeným výsledkům a rozdílné rozložení míry této nepřesnosti podobu typického pracovního cyklu, tj. 1 roku. Tradiční inženýrské řešení, vycházející z tvarového faktoru, jedna metoda založená na aplikaci teorie energetického zdroje a energ. propadu (dle Lit. [13]), a dvou analytických metod, normalizovaných v mezinárodním měřítku, jsou v Tabulce 3.1.1. porovnány s hodnotami naměřenými, přesněji vypočítanými z naměřených hodnot, s ohledem na minima a maxima odchylek po jednotlivých sekvencích měření.
| Období / výpočtová metoda | 27.Mar– 29.Mar 2014 | 10.Jun 2014 | 18.Nov– 03.Dec 2014 | 04.Dec– 30.Dec 2014 | 30.Dec 2014– 05.Feb 2015 | 27.Aug– 28.Aug 2015 | 08.Sep– 13.Oct 2015 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ČSN EN 13 941 | −1,1 | −0,3 | +2,31 | +2,4 | −1,5 | +0,6 | −14,8 | −0,2 | −3,7 | −1,2 | +3,5 | +3,6 | +0,1 | +3,4 |
| ČSN EN ISO 12 241 | −0,9 | −0,3 | −1,6 | −1,6 | +1,6 | +3,3 | +0,8 | +3,7 | −0,1 | −3,6 | −1,4 | +0,4 | −0,8 | +4,1 |
| Literatura [13] | −4,5 | −2,8 | −3,9 | −3,8 | −1,4 | −0,3 | −0,6 | +2,6 | −2,5 | −0,4 | −3,5 | −1,8 | −3,0 | +0,6 |
| Tvarový faktor | −14,0 | −8,4 | −17,7 | −17,3 | +6,4 | +17,4 | +0,6 | +19,8 | −4,9 | +18,9 | −14,9 | −1,5 | −10,6 | +22,8 |
Maximální a minimální odchylky výsledků tepelných ztrát jednotlivých analytických metod, ve srovnání s hodnotami naměřenými, jsou uvedeny v Tabulce 3.1.2. Tabulka obsahuje i hodnotu průměrné odchylky tepelného toku z potrubní konstrukce od naměřené hodnoty a průměrnou velikost absolutní hodnoty odchylky za celou dobu měření ve W/m.
| Výpočtová metoda | Max. (−) odchylka od naměřených výsledků | Max. (+) odchylka od naměřených výsledků | Průměrná velikost odchylky s ohledem na směr odchylky | Průměrná velikost absolutní hodnoty odchylky |
|---|---|---|---|---|
| ČSN EN 13 941+A1 | −14,8 | +3,6 | −2,0 (8,8 %) | 4,7 |
| ČSN EN ISO 12 241 | −1,6 | +4,1 | +2,0 (8,9 %) | 2,1 |
| Literatura [13] | +0,6 | −4,5 | −0,7 (3,0 %) | 1,5 |
| Tvarový faktor | +17,7 | −22,8 | +8,7 (39,0 %) | 10,3 |
Podrobněji, po jednotlivých sekvencích měření, jsou odchylky jednotlivých analytických výpočtů od naměřených hodnot, s ohledem na směr odchylky, uvedeny v Tabulce 3.1.3.
| Období / výpočtová metoda | 27.Mar– 29.Mar 2014 | 10.Jun 2014 | 18.Nov– 3.Dec 2014 | 04.Dec– 30.Dec 2014 | 30.Dec 2014– 05.Feb 2015 | 27.Aug– 28.Aug 2015 | 08.Sep– 13.Oct 2015 |
|---|---|---|---|---|---|---|---|
| ČSN EN 13 941+A1 | −0,6 | +2,3 | −0,4 | −8,8 | −2,2 | +3,5 | +2,5 |
| ČSN EN ISO 12 241 | −0,6 | −1,6 | +2,6 | +2,2 | −2,1 | −0,3 | +1,6 |
| Literatura [13] | −3,4 | −3,8 | −0,9 | +1,5 | −1,6 | −2,5 | −1,0 |
| Tvarový faktor | −10,8 | −17,6 | +13,0 | +10,2 | +8,4 | −7,1 | +7,0 |
Na základě naměřených hodnot a provedených výpočtů je možno konstatovat, že výpočet dle specializované normy ČSN EN 13 941+A1 se ukázal, ve srovnání s naměřenými hodnotami ve standardní lokalitě, jako nepříliš přesný. Význam tohoto výpočtu lze vidět především v použití pro posouzení tepelných ztrát v delším období (alespoň 1 rok), kdy tento výpočet může vykazovat odchylky do 10 % od hodnot získaných přesným měřením. Především pro kratší období (méně než 1 rok) je výrazným problémem této metodiky výpočtu tepelné ztráty teplovodu/horkovodu stanovení okamžité teploty okolní, předmětným tepelným zdrojem nezasažené, zeminy.
Velmi jednoduchý výpočet dle ČSN EN ISO 12 241, jehož reálná použitelnost pro souběhy topných, či chladicích, potrubí, je na první pohled méně předpokládatelná, vykazoval, a to po celou dobu měření, značnou blízkost s naměřenými hodnotami. Překvapivé je to především s ohledem na předpokládané významnější tepelné ovlivňování obou potrubí. Skutečnost, že vzájemné ovlivnění přívodního a vratného potrubí uvnitř potrubní konstrukce je nižší, než bylo možno očekávat, zřejmě souvisí s účinnou tepelnou izolací každé z jednotlivých trubek, která brání tomuto vzájemnému vlivu, a také s naměřenou poměrně nízkou hodnotou tepelné vodivosti zeminy v bezprostředním okolí potrubní konstrukce.
Výpočtový postup za použití tvarového faktoru je velmi rychlým způsobem získání informace o předpokládatelné tepelné ztrátě. Vzhledem k jednoduchosti této metody je možno odchylky od naměřených hodnot v řádu 30–40 % měřené hodnoty považovat za odpovídající rychlosti výpočtů. Zásadní nevýhodou tohoto způsobu výpočtu je malá možnost jeho využití k okamžitému výpočtu tepelné ztráty potrubní trasy v letním období. Tím, že výpočet počítá pouze s teplotním gradientem mezi proudícím médiem a teplotou na povrchu země, dochází v době relativně vysoké povrchové teploty země (duben–září) ke značnému zkreslení vypočtených hodnot tepelných ztrát.
Přínosem posledních dvou uvedených postupů pro technickou praxi je poměrně snadné zjištění všech potřebných vstupních údajů. Většina z nich je trvale měřena jako provozní údaj CZT, či jsou archivovány ČHMÚ. Ohraničující teploty těchto dvou metodik výpočtu nejsou, na rozdíl od výpočtu tepelné ztráty dle ČSN EN 13 941+A1, voleny, či vypočítávány z historických údajů.
Po srovnání naměřených hodnot s hodnotami vypočtenými se jako nejpřesnější jeví, z pohledu více než jeden a půl ročního měření, výpočtová metoda pracující s modelem energetického zdroje a propadu, zahrnující v sobě superpoziční principy, popsaná doc. Karlem Brožem např. v literatuře [13]. Průměrná odchylka mezi tepelnou ztrátou, získanou výpočtem s využitím naměřených teplot a hodnotou této ztráty získanou metodou superpozice, byla 2,99 % s tím, že max. hodnota zaznamenaná odchylky pro jednotlivé měření byla 4,49 W/m. Vzhledem k tomu, že i velikost průměrné odchylky získané jako průměr kvadrátu odchylek je v tomto případě výrazně nižší, než u ostatních výpočtových metod, je zřejmé, že tuto metodu je možno doporučit jako nejlepší.
2/ Na základě posouzených úseků teplotního pole, viz, tabulky výše, je z výsledků měření zřejmé, že tepelná vodivost písčitých i hlinitopísčitých zemin v bezprostředním okolí horkovodů se blíží, zřejmě i v souvislosti s nevýznamnou přítomností chemicky nenavázané vody, spíše k minimálním hodnotám uvedeným v literatuře. V žádné části měřeného teplotního pole nikde, a to ani vzdáleně, nedosáhla tepelná vodivost v konkrétně vyšetřované oblasti hodnoty tepelné vodivosti λE = 2,0 W/mK, která je v odborné literatuře poměrně často zmiňována. Nelze samozřejmě zevšeobecňovat výsledky z jedné měřené lokality, ale z předložených hodnot může být usuzováno alespoň tolik, že tepelná vodivost poměrně suchých písčitých zemin v okolí horkovodních sítí může dosahovat i velmi nízkých hodnot, viz např. výše uvedená hodnoty získané z naměřených hodnot. Při predikci tepelných toků v okolí podzemních sítí je vhodné na tuto možnost brát zřetel.
Tato informace může být zásadní především při návrhu pěnových podušek, určených pro zachycení dilatací potrubí vzniklých v souvislosti se změnami přívodní teploty u horkovodů. V případě malé tepelné vodivosti okolní zeminy může dojít, a to díky interakci izolačních schopností PUR či PE plastových dilatačních podušek a zásypové zeminy, k přehřátí HDPE krycího pláště izolovaného potrubí.
3/ Z hodnot naměřených tepelných ztrát je patrné, že při obvyklé hloubce zásypu potrubí jsou hodnoty tepelných ztrát v měsících mimo topné období nízké, a nezavdávají pro většinu teplárenských sítí podnět pro nutnost výstavby tvz. „letního rozvodu“ tepelné energie.
Hlavními příčinami zaznamenané nízké tepelné ztráty v letním provozu jsou především naměřené vysoké hodnoty teploty v oblasti mezi povrchem země a potrubím během tohoto období, a současně i výrazné snížení teploty teplonosné látky v potrubí během dodávky tepla pouze pro účely ohřevu pitné vody pro hygienické účely. Měření v lokalitě prokázalo prohřátí podstatné výšky měřeného teplotního pole již během měsíce června do takové míry, že dojde k minimalizaci teplotního gradientu především mezi vratným potrubím a jeho okolím, a tento stav setrvá přibližně až do konce října. V případech, kdy je rozdíl mezi zímní a letní spotřebou natolik výrazný, že investice do letního rozvodu je předmětem úvahy, nabízí tato práce jako kompromisní řešení aplikaci pouze třetí, dodatečné, potrubní linie, namísto montáže celého nového „letního“ = mimosezonního dvoutrubního rozvodu. V dalších článcích navrhne autor i výpočtový aparát pro výpočet izolačního vlivu tohoto třetího potrubí pro období, kdy jím neprochází žádný průtok.
4. Doporučená literatura k tématu tepelných jevů v teplárenských sítích
- JANNA, William S.; Engineering heat transfer, 3rd etition. Broken Sound Parkway NW: CRC Press, Taylor & Francis Group, 2009. 1 sv. 12 kapitol s. ISBN 978-1-4200-7202-0.
- VLACH, Josef, a kol.; Zásobování teplem a teplárenství. Vydání 1. Praha: SNTL, 1989. 552 s. 04-207-89
- HAICHAO, Wang; WENLING, Jiaoand; CHUANZHI, Zhu; Design and Operation Regulation of Combined Heating System with Gas-Fired Boilers as Peak-Load Heat Sources in Secondary Heating Network., Intelligent Computation Technology and Automation (ICICTA), 2011 International Conference 2011.
- KOLAŘÍK, Jakub; Tepelná pohoda a pracovní výkonnost v budovách s kolísáním operativní teploty. TZB Haus Technik: Technická zařízení budov. 2010, III., 3, s. 17–19. ISSN 1803-4802.
- Yan Li; Lin Fu; Shigang Zhang; Yi Jiang; Zhao Xiling; A new type of district heating method with co-generation based on absorption heat exchange (co-ah cycle)., Department of Building Science, Tsinghua University, PR China, Energy Conversion and Management, Volume 52, Issue 2, February 2011, Pages 1200-1207
- JALURIA, Yogest; TORRANCE, Kenneth E.; Computational Heat Transfer: series in computational and physical processes in mechanics and thermal sciences. 2. vydání. 29 West 35th Street New York NY 10001: Taylor & Francis, 2003. 2. edice, TJ260 .J35 2002. ISBN 1-56032-477-5.
- CHANG, Yoon-Suk, a kol.; Fatigue Data Acquisition, Evaluation and Optimization of District Heating Pipes. Applied Thermal Engineering, 10, 2007, vol. 27, no. 14–15. pp. 2524–2535. Přístupné z
http://www.sciencedirect.com/science/article/pii/S1359431107000725. ISSN 1359-4311. - The 11th International Symposium on District Heating and Cooling; August 31 to September 2, 2008, Reykjavik, ICELAND, Sborník příspěvků.
- BOHM Benny; KRISTJANSSON Halldor; Single, twin and triple buried heating pipes: on potential savings in heat losses and costs. INTERNATIONAL JOURNAL OF ENERGY RESEARCH. Int. J. Energy Res. 2005; 29:1301–1312 Publikováno online 18. července 2005 Wiley InterScience, dostupný z www.interscience.wiley.com. DOI: 10.1002/er.1118.
- BENONYSSON, Atli; BOHM, Benny; RAVN, Hanz; Energy Conversion and Management, 1996, Volume 36, Str. 297–314, článek dostupný z
http://ac.els-cdn.com/019689049598895T/1-s2.0-019689049598895T-main.pdf?_tid=ab8b995cebb6abeda5da6cdc656b5b13&acdnat=1339690992_9f9c810cdd82da1038aa46339e89367b. - BOHM, Benny; On transient heat losses from buried district heating pipes. INTERNATIONAL JOURNAL OF ENERGY RESEARCH [online]. 2000, 24, [cit. 2011-04-22]. Článek dostupný z:
http://80.onlinelibrary.wiley.com.dialog.cvut.cz/doi/10.1002/1099-114X(200012)24:15%3C1311::AID-ER648%3E3.0.CO;2-Q/abstract. - RANDLOV, Peter; The District Heating Handbook. 1. vyd. Fredericia Danmark: European District Heating Pipe Manufacturers Association, 1997. 2. ISBN 87-90488-03-2. str. 176.
- BROŽ, Karel; VYDAVATELSTVÍ ČVUT. Zásobování Teplem. 1. vydání. Praha: Ediční středisko ČVUT, 1997. ISBN 80-01-01587-4.
The article deals with the measurement of temperature field around the underground pipeline and compared heat losses derived from the measured values, the values calculated by different methodologies and its content fits into a several-cycle of articles on the topic of heat transfer in the field of underground pipeline in terms of quantifying heat loss and the extent and the intensity of the thermal field generated in the vicinity of the pipeline network.
