Analýza termodynamických jevů v potrubních sítích IV.
Teoretické základy – hydraulika ocelového teplárenského potrubí
Článek volně pokračuje v tématu analýzy termodynamických jevů vyskytujících se uvnitř a v okolí potrubní konstrukce umístěné v sypkém zásypu, nyní s ohledem na teoretické základy popisující hydraulické jevy. Článek obsahuje především aktuálně známé náhledy do problematiky proudění teplonosné látky ocelovým horkovodním potrubím používaným v teplárenství a předkládá autorem vypočtené hodnoty potřebných vstupních údajů pro určení hydraulických ztrát.
Teoretická východiska
Základními teoretickými východisky jsou zákony o zachování energie, Fourierův zákon vedení tepla, Bernoulliho rovnice, rovnice kontinuity, teorie proudění Newtonovských kapalin a zhodnocení reálných Neumannových a Dirichletových okrajových podmínek pro řešení parciálních diferenciálních rovnic vedení tepla jednotlivými izolačními vrstvami. V oboru proudění kapalin jsou velmi často využívány výsledky výzkumů Nikuradseho, Colebrookovy, Whiteovy, Moodyho, Gessnerovy a rovnice Darcy-Weisbachovy.
Výpočtové postupy
Proudění nevazké nestlačitelné tekutiny v silovém poli je popsáno diferenciálním tvarem Bernoulliho rovnice
kde s je délka měřená podél proudnice, h je pořadnice bodu proudnice od libovolné vodorovné srovnávací roviny (tedy výška), p je tlak, v je rychlost a τ je čas.
Proudění kapaliny potrubím je, z hlediska hydraulického, po celou dobu provozu potrubní soustavy ovlivňováno hydraulickými ztrátami, které vznikají při proudění teplonosné či chladicí látky potrubím, výměníky, uzavíracími a regulačními armaturami a tvarovými částmi potrubních tras. Problematika řešení hydraulických ztrát v potrubí různých průřezů je poměrně podrobně popsána např. v literatuře [22] a [23].
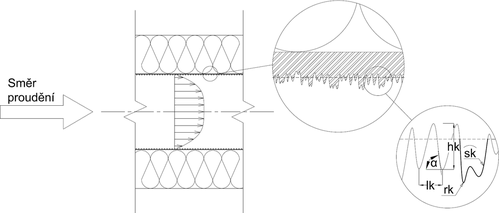
Disipace energie (hydraulická ztráta) kapaliny proudící potrubím je dána především jeho hydraulickým průřezem (v případě potrubí kruhového průřezu je tento identický s vnitřním průměrem potrubí), rychlostí proudění kapaliny potrubím v, průběhem rychlostního profilu a úhlem (zakřivením) trubního dílu. Výrazný vliv na hydraulickou ztrátu mají i vlastnosti vnitřního povrchu potrubí (viz Obrázek 1), mj. i tzv. hydraulická drsnost.
Ustálené izotermické proudění vazké nestlačitelné kapaliny potrubím je možno popsat nejlépe za pomoci energetického tvaru Bernoulliho rovnice (v praxi bývají její složky vyjádřeny v různých formách, fyzikální veličiny pak bývají dosazovány v různých jednotkách). Nachází-li se kapalina v poli konzervativních sil (práce vykonaná na uzavřené křivce v izolovaném systému je nulová), je celková mechanická energie kapaliny E dána jako
kde ![]() je kinetická energie, Ep = p ‧ V je tlaková energie a Eg = m ‧ g ‧ h je energie potencionální.
je kinetická energie, Ep = p ‧ V je tlaková energie a Eg = m ‧ g ‧ h je energie potencionální.
Existence potenciální tlakové energie Ep vyplývá z následujícího: na kapalinu v trubce kruhového průřezu působí síla F, kapalina tak urazí dráhu s, proto tato síla vykoná práci W = F ‧ s. Dále víme, že síla F = p ‧ A, kde A je průřez potrubí, takže po dosazení do vztahu pro práci W plyne W = p ‧ A ‧ s = p ‧ V. Tato práce W odpovídá potenciální tlakové energii. Po dosazení jednotlivých energií do výše uvedeného vztahu platí:
Pokud energie vyjádříme ve formě měrných energií (vztažených na 1 kg kapaliny), pak pro dva navazující průřezy potrubí bude při proudění nevazké kapaliny platit:
V případě, že si přejeme vyjádřit disipaci energie, která pohyb vazké kapaliny potrubím vždy provází, můžeme ji vyjádřit buď jako ztrátovou měrnou energii nebo jako tzv. ztrátovou výšku hz, uvedenou na pravé straně rovnice
Tato ztrátová výška hz [m] vyjadřuje disipaci energie kapaliny na úseku potrubí mezi dvěma následujícími průřezy, situovanými ve výšce h0 a ve výšce h1 od zvolené vztažné roviny.
Ztrátovou výšku hz lze vyjádřit jako součet dílčích ztrátových výšek:
- třením na přímém potrubí o délce potrubí ht,
- místními vlivy (tvarové kusy, armatury) hm.
Někdy je v oboru potrubní hydrauliky používán jiný tvar Bernoulliho rovnice:
kde γ je tíha [N/m3] a všechny a členy této rovnice mají rozměr tlaku [Pa].
Pro stanovení správné hodnoty hydraulické ztráty je možno využít v souvislosti s teorií podobnosti Reynoldsovo číslo. Z teorie podobnosti vyplývá, že dva jevy, na něž působí výhradně nebo převážně síly vnitřního tření, jsou si podobny, mají-li totéž Reynoldsovo číslo ![]() .
.
Reynoldsovo číslo je tak možno použít při určení součinitele tření pro velký rozsah průměrů potrubí a rychlostí proudění kapaliny, viz Obrázek 2.
Druhou základní rovnicí je rovnice kontinuity (rovnice spojitosti toku tekutiny). Pro neustálené proudění stlačitelné tekutiny v proudové trubici platí rovnice v diferenciálním tvaru:
kde A je průřezová plocha (např. průtočného průřezu potrubí) a s je dráha, kterou tekutina urazí v čase τ.
V případě ustáleného proudění je pak možno tuto rovnici použít ve tvaru ς ‧ v ‧ A = konst., což je rovnice kontinuity pro ustálené proudění stlačitelné tekutiny v proudové trubici.
Při ustáleném proudění, kdy parciální derivace hustoty podle času ![]() , tedy nedochází ke změně hustoty protékající látky (jedná se o nestlačitelnou tekutinu), tato rovnice přechází do tvaru v ‧ A = konst.
, tedy nedochází ke změně hustoty protékající látky (jedná se o nestlačitelnou tekutinu), tato rovnice přechází do tvaru v ‧ A = konst.
Jestliže označíme jednotlivé průřezy trubice jako 0, 1, 2, 3, ……………n, je možno, pro objemový průtok trubicí Q, psát, že
Výše hydraulické ztráty vznikající při proudění topné látky (vazké kapaliny) ocelovým potrubím kruhového průřezu je dána především střední rychlostí proudění a geometrickými vlastnostmi potrubí (viz Obrázek 1), tedy především vnitřním průměrem D, tvarem, orientací a výškou (hloubkou) nerovností vnitřního povrchu a u tvarových kusů potrubí také zakřivením a členěním protékaného prostoru (oblouky, kolena, ohyby, T-odbočky). Hydraulická ztráta je rovněž určena vlastnostmi protékající teplonosné látky s ohledem na její chování během pohybu uvnitř potrubí. Pro kvantifikaci jejího chování, s ohledem na třecí ztráty během proudění, je možno s výhodou využít kinematickou viskozitu ϑ.
Geometrie dopravovanou kapalinou obtékaného povrchu trub, resp. kvalita tohoto povrchu, je nejčastěji posuzována relativní drsností povrchu k / D, kde k je absolutní drsnost povrchu potrubí a D vnitřní průměr posuzovaného kruhového potrubí, což však v mnoha případech nemusí být pro popsání vlastností potrubí dostačující. Teplárenské potrubí lze, po většinu doby jeho provozu, považovat v hydraulickém smyslu za potrubí s vráskovitou drsností (popsáno Gessnerem). K popisu jeho hydraulických vlastností je možno použít součinitel tření λ, který by měl vyjadřovat plný vliv drsnosti, resp. vliv všech, nebo alespoň většiny známých parametrů ovlivňujících hydraulickou ztrátu. Součinitel tření je z tohoto pohledu možno vyjádřit jako veličinu, závisející i na jednotlivých geometrických parametrech potrubí a veličinách charakterizujících proud kapaliny
kde hk je radiální výška prvků drsnosti, lk je vzdálenost prvků drsnosti stěny ve směru proudění (rozteč), sk je obvodová délka prvku drsnosti, rk je poloměr zakřivení prvku drsnosti a α je úhel mezi sklonem náběhové plošky a osou proudění, jak je patrné z Obrázku 1.
Výpočty
V případě moderních teplárenských potrubních sítí s dlouhodobě funkční úpravou oběhové vody lze pro stanovení vhodného hydraulického průřezu (a následně nejbližšího normalizovaného DN) pro požadovaný průtok předpokládat potrubí ocelové, kruhového průřezu, podélně či spirálně svařované. Hodnotu absolutní drsnosti pro toto potrubí lze uvažovat k ≤ 0,1 mm, se střední hodnotou k = 0,08 mm. Protože se při proudění v posuzovaném trubním úseku u většiny horkovodů jedná o proudění v oblasti přechodové, či v oblasti plně rozvinutého turbulentního proudění, můžeme pro přechodovou oblast využít při určení součinitele tření λ např. vztah Colebrook-Whiteův:
Při větších Reynoldsových číslech Re → ∞ se takto stanovené hodnoty součinitele tření blíží hodnotám stanoveným podle vztahu Nikuradseho:
Pro technické výpočty je často využíván Šerekův explicitní tvar Colebrook-Whiteovy rovnice:
který je platný pro 4 000 < Re < 80 000. V oblasti, kde Re ›› 80 000, vykazují hodnoty součinitele tření, vůči J. Nikuradsem uskutečněným měřením, pouze menší odchylku.
Pro potrubí, jehož posuzování je předmětem našeho zájmu, tedy pro běžné potrubí horkovodních teplárenských soustav, lze předpokládat, že pro proudění uvnitř vratné linie, přibližně při hodnotě Reynoldsova čísla Re = 250 000, bude hodnota součinitele tření λ v potrubí, např. dle Colebrook-Whitea
V případě proudění uvnitř potrubí přívodního se často při velkých rychlostech proudění vody cca v okolí Re = 700 000 jedná již o plně rozvinuté turbulentní proudění, kde součinitel tření přestává být závislý na Reynoldsově čísle a k jeho výpočtu je možno s dostatečnou přesností použít pouze geometrické charakteristiky potrubí, tzn., že λ = f (k / D). Na základě Nikuradseho vzorce i upřesněného grafu dle [26] (viz Obrázek 2), je předpokládatelná přibližná hodnota součinitele tření v přímých úsecích potrubí
![Obrázek 2 – Doporučené hodnoty součinitele tření pro komerčně vyráběná potrubí dle [26]. Symbol CW – dle Colebrook White, symbol PM – dle prezentovaného modelu, D je vnitřní průměr vyšetřovaného potrubí. Jednotky – Re[1], λ[1]](/docu/clanky/0133/013335o18.png)
Obrázek 2 – Doporučené hodnoty součinitele tření pro komerčně vyráběná potrubí dle [26]. Symbol CW – dle Colebrook White, symbol PM – dle prezentovaného modelu, D je vnitřní průměr vyšetřovaného potrubí. Jednotky – Re[1], λ[1]
Pro potrubí, používaná v teplárenských sítích, lze při stanovení hydraulické ztráty horkovodu, využít ke stanovení hodnoty absolutní drsnosti následující doporučení dle [13]:
| Absolutní drsnost povrchu k [mm] | |
|---|---|
| nové ocelové trubky tažené | 0,01–0,05 |
| nové ocelové trubky válcované | 0,04–0,1 |
| nové ocelové trubky svařované | 0,05–0,1 |
| ocelové trubky s mírně orezavělým povrchem | 0,15–0,2 |
| ocelové trubky mírně orezavělé se slabým nánosem | 0,15–0,5 |
| ocelové trubky se silnějšími inkrustacemi | až 1,5 i více |
V souvislosti s výrobními postupy používanými pro výrobu ocelového teplárenského svařovaného potrubí – jedná se většinou o technologii podélného svařování potrubí z plechových svitků, lze předpokládat dlouhodobě konstantní rozměrové vady povrchu. Tyto vady jsou dány především kvalitou plechového polotovaru – svitku, vzniklého válcováním za tepla, ev. za studena. U těchto svitků jsou absolutní velikosti geometrických charakteristik vnitřního povrchu popsaných hodnotami hk, lk, sk, rk, α (viz Obrázek 1) a především absolutní drsnosti k téměř shodné. Tato přibližná shoda platí pro rozsah jmenovitých světlostí trub používaných v rámci okrskových horkovodních topných rozvodů, tedy DN 20 – DN 200.
V těchto případech, kdy k = konst. ≈ 0,08 mm, bude λ = f (k / D, Re).
Pro hodnotu rychlosti proudění topné vody v = 2 m/s a její střední teplotu cca 80 °C byla numericky v závislosti na Reynoldsově čísle (přesněji na druhu proudění), z White-Colebrookova vztahu a Nikuradseho rovnice, vypočítána hodnota λ, uvedená v Tabulce 3.
| DN | 20 | 25 | 32 | 40 | 50 | 65 | 80 | 100 | 125 | 150 | 200 |
| Re [1] | 122990 | 161530 | 210840 | 244280 | 308890 | 398440 | 467580 | 607010 | 750970 | 908530 | 1190800 |
| Druh proudění | T | T | T | T | T/PRT | T/PRT | T/PRT | T/PRT | PRT | PRT | PRT |
| λ [1] | 0,0287 | 0,0265 | 0,0247 | 0,0237 | 0,0223 | 0,0209 | 0,0201 | 0,0183 | 0,0174 | 0,0167 | 0,0157 |
Je možno uvést, že při celkové délce potrubní sítě v oblasti běžného teplárenského okrsku – cca 2–5 km trasy, tedy 4–10 km potrubí (v případě nejčastěji používaného dvoutrubního zapojení) a při velmi častém jmenovitém průměru DN = 80 mm, kolísá hydraulická ztráta především v závislosti na rychlosti průtoku (1,5–2,5) m/s. Tlaková ztráta přímého potrubí v takovémto okrsku, při použití Darcy-Weisbachova vzorce:
po dosazení rychlosti 1,5 m/s do tohoto vzorce:
a pro rychlost 2,5 m/s:
pak vychází v rozsahu od 1,88 MPa po 5,21 MPa. Pro uvedený výpočet je předpokládána délka přímého potrubí 7 km a střední teplota teplonosné látky (vody) 70 °C. Je patrné, že i při tomto poměrně malém rozdílu rychlosti (o pouhý 1 m/s) se zvýší hydraulické ztráty v rovném potrubí zhruba na necelý trojnásobek. Z Darcy-Weisbachovy rovnice tedy plyne, že tlaková ztráta může být vyjádřena ve vazbě na dynamický tlak, který určuje součinitel λ.
Pokud se hustota protékající kapaliny na uvažované délce potrubí mění, volí se střední hodnota hustot mezi začátkem a koncem uvažovaného úseku. Jako porovnávací dynamický tlak je předpokládán dynamický tlak (úměrný rychlosti v daném místě) na vstupu do hydraulicky propočítávaného prvku, ke kterému bývá vztažen i součinitel místní ztráty. Z důvodu, že ztrátový součinitel je funkcí tvaru a velikosti potrubního prvku (a při určitých rychlostech proudění i funkcí Reynoldsova čísla), uvádějí někdy výrobci potrubí a potrubních tvarovek pro jeden potrubní prvek několik hodnot ztrátového součinitele (podle druhu pracovní látky, teploty, tlaku a objemového průtoku). Celková hydraulická ztráta potrubní sítě, která je zásadní pro určení výtlačné výšky oběhového čerpadla nebo sady čerpadel, je pak dána součtem tlakových ztrát v přímých úsecích potrubní sítě a ztrát v jednotlivých potrubních tvarových kusech (např. oblouky, T-odbočky) a v uzavíracích a regulačních armaturách.
Pro tento souhrnný výpočet hydraulických ztrát jsou velmi často využívány tzv. ekvivalentní délky potrubí nahrazující konkrétní tvarové kusy nebo armatury (lokální hydraulické odpory). Lokální odpor se nahrazuje přímým potrubím odpovídající DN určité délky, na které by byla stejná hydraulická ztráta, jakou by způsobil příslušný lokální odpor. Tyto ekvivalentní délky jsou přičteny k celkové délce rovného potrubí a celková tlaková ztráta se určí pomocí Darcy-Weisbachova vztahu.
Závěr
V současné době, kdy je každé projekční pracoviště vybaveno alespoň základní výpočetní technikou, není nikterak složité samostatně vytvořit, či využívat komerčně vytvořený program, který postupnými aproximacemi vypočte všechny podstatné hydraulické parametry vyšetřované sítě. Přesto je třeba, i na základě výše uvedeného, mít neustále přehled o vstupních a vypočítaných hodnotách, zejména ve vztahu k fyzikálním zákonům, empirickým vzorcům a diagramům, platným v oboru mechaniky tekutin. Rovněž je důležité mít přehled o aktuálně platné energetické legislativě.
Je nutno mít stále na paměti, že správný hydraulický návrh teplárenské potrubní sítě, spolu s volbou vhodného energetického zdroje, rozhoduje, a to nejen v době montáže, ale po celou dobu její životnosti, o efektivním či ztrátovém provozu celé teplárenské soustavy.
Dodatečně umisťované izolace či změny provozních režimů, směřující ke snížení hydraulických i tepelných ztrát, mohou následně již pouze mírně ovlivnit důsledky hydraulicky nesprávného návrhu potrubní sítě.
Seznam použitých symbolů a zkratek
| Označení v textu | Význam | Jednotka |
|---|---|---|
| T | absolutní teplota | K |
| t | teplota | °C |
| ς | měrná hmotnost (hustota) | kg/m3 |
| L | délka | m |
| λ | součinitel tření | [1] |
| Re | Reynoldsovo číslo | [1] |
| q | měrný tepelný tok vztažený k jednotce délky či plochy | W/m [W/m2] |
| C | osová rozteč | m |
| A | plocha kolmá ke směru toku | m2 |
| s | dráha | m |
| r | poloměr | m |
| α | úhel | rad |
| p Δp | tlak tlaková ztráta | Pa Pa |
| h hz | hloubka/ výška ztrátová výška | m m |
| D | vnitřní průměr potrubí | m |
| v | rychlost | m/s |
| g | tíhové zrychlení | m/s2 |
| F | síla | N |
| m | hmotnost | kg |
| τ | čas | s |
| q | kinematická viskozita | m2/s |
| k | absolutní drsnost povrchu | mm |
| z | rozdíl výšek | m |
| E | energie měrná energie | J J/kg |
| W | práce | J |
| γ | měrná tíha | N/m3 |
| n | označení čísla průřezu | [1] |
| α | úhel sklonu náběhové plošky | rad |
| Q | objemový průtok | m3/s |
| V | objem | m3 |
| Zkratka | Plný význam |
|---|---|
| DN | „Diameter nominal“ – jedná se o označení určující přibližně velikost příslušných součástí potrubí, a to zpravidla ve vztahu k jejich skutečnému vnitřnímu průměru |
| PRT | Plně rozvinuté turbulentní proudění |
| T | Turbulentní proudění |
| PM | dle prezentovaného modelu |
| CW | dle Colebrook-Whitea |
Doporučená literatura k tématu teplárenských sítí
- [1] JANNA, William S. Engineering heat transfer 3rd etition. Broken Sound Parkway NW: CRC Press, Taylor & Francis Group, 2009. 1 sv. 12 kapitol s. ISBN 978-1-4200-7202-0.
- [2] VLACH, Josef, a kol. Zásobování teplem a teplárenství. Vydání 1. Praha: SNTL, 1989. 552 s. 04-207-89
- [3] HAICHAO, Wang; WENLING, Jiaoand CHUANZHI, Zhu. Design and Operation Regulation of Combined Heating System with Gas-Fired Boilers as Peak-Load Heat Sources in Secondary Heating Network., Intelligent Computation Technology and Automation (ICICTA), 2011 International Conference 2011.
- [4] KOLAŘÍK, Jakub. Tepelná pohoda a pracovní výkonnost v budovách s kolísáním operativní teploty. TZB Haus Technik: Technická zařízení budov. 2010, III., 3, s. 17–19. ISSN 1803-4802.
- [5] Yan Li, Lin Fu, Shigang Zhang, Yi Jiang and Zhao Xiling, A new type of district heating method with co-generation based on absorption heat exchange (co-ah cycle)., Department of Building Science, Tsinghua University, PR China, Energy Conversion and Management, Volume 52, Issue 2, February 2011, Pages 1200–1207
- [6] LAKEW, Amlaku Abie; BOLLAND, Olavand LADAM, Yves. Theoretical Thermodynamic Analysis of Rankine Power Cycle with Thermal Driven Pump. Applied Energy, 9, 2011, vol. 88, no. 9. pp. 3005-3011. Přístupné z
http://www.sciencedirect.com/science/article/B6V1T-52KVR4R-3/2/4feb0b2d78185e086a8748133739713e. ISSN 0306-2619. - [7] CHANG, Yoon-Suk, et al. Fatigue Data Acquisition, Evaluation and Optimization of District Heating Pipes. Applied Thermal Engineering, 10, 2007, vol. 27, no. 14–15. pp. 2524–2535. Přístupné z
http://www.sciencedirect.com/science/article/pii/S1359431107000725. ISSN 1359-4311. - [8] The 11th International Symposium on District Heating and Cooling, August 31 to September 2, 2008, Reykjavik, ICELAND, Sborník příspěvků.
- [9] BOHM Benny, KRISTJANSSON Halldor, Single, twin and triple buried heating pipes: on potential savings in heat losses and costs. INTERNATIONAL JOURNAL OF ENERGY RESEARCH. Int. J. Energy Res. 2005; 29:1301–1312 Published online 18 July 2005 in Wiley InterScience, dostupný z www.interscience.wiley.com. DOI: 10.1002/er.1118.
- [10] PERSSON, Urban; WERNER, Sven. Heat distribution and the future competitiveness of district heating. Applied Energy [online]. 4.June 2010, 88, [cit. 2011-04-11]. Článek dostupný z www.elsevier.com/locate/apenergy.
- [11] BOHM, Benny. On transient heat losses from buried district heating pipes. INTERNATIONAL JOURNAL OF ENERGY RESEARCH [online]. 2000, 24, [cit. 2011-04-22]. Článek dostupný z http://80.onlinelibrary.wiley.com.dialog.cvut.cz/doi/10.1002/1099-114X(200012)24:15%3C1311::AID-ER648%3E3.0.CO;2-Q/abstract.
- [12] RANDLOV, Peter. EUROPEAN DISTRICT HEATING PIPE MANUFACTURERS ASSOCIATION. The District Heating Handbook. 1. vyd. Fredericia Danmark: European District Heating Pipe Manufacturers Association, 1997. 2. ISBN 87-90488-03-2. str. 176.
- [13] BROŽ, Karel. VYDAVATELSTVÍ ČVUT. Zásobování Teplem. 1. vyd. Praha: Ediční středisko ČVUT, 1997. ISBN 80-01-01587-4.
- [14] TARNAWSKI, Vlodek R. a Wey H. LEONG. A Series-Parallel Model for Estimating the Thermal Conductivity of Unsaturaded Soils. International Journal of Thermophysics 2012, roč. 2012, č. 33, s. 1191–1218. DOI: 10.1007/s10765-012-1282-1. Dostupné z: http://80.download.springer.com.dialog.cvut.cz/static/pdf/158/art%253A10.1007%252Fs10765-012-1282-1.pdf?auth66=1391680471_9a9214f2ea6d15d40c67dff38825f93d&ext=.pdf
- [15] IMA- Dresden, Result list of thermal conductivity measurement and density determination, 11. 12. 2013, archiv Oddělení kvality společnosti Uponor Infra Fintherm a.s., Za Tratí 197, Praha 9.
- [16] PERPAR, Matjaz, et al. Soil Thermal Conductivity Prediction for District Heating Pre-Insulated Pipeline in Operation. Energy. 2012, vol. 44, no. 1, s. 197–210. Dostupné z: http://www.sciencedirect.com/science/article/pii/S0360544212004884. ISSN 0360-5442.
- [17] Úřad pro technickou normalizaci, metrologii a státní zkušebnictví, česká technická norma ČSN EN 13941+A1, Navrhování a instalace bezkanálových předizolovaných sdružených potrubních systémů pro vedení vodních tepelných sítí, ICS 23.040,10; 91.140.10.
- [18] KOZEL, Karel. ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE. Numerické řešení parciálních diferenciálních rovnic. 1. vyd. Praha: ČVUT, 2000. Učební texty Praha ČVUT fak. stroj. ISBN 80-01-02166-1. Dostupné z:
http://k4.techlib.cz/search/handle/uuid:2a542310-b680-40a8-846e-704883dbcb88 - [19] LABOUTKA, K., SUCHÁNEK, T. TZB-info: Tabulky a výpočty: Vybrané výpočetní
- vztahy pro vlastnosti vody [online]. 2001 [cit. 2009-05-26]. Dostupné z: http://www.tzb-info.cz/t.py?t=16&i=41&h=38&obor=1.
- [20] ŠOB, F. Hydromechanika. Brno: Akademické nakladatelství CERM s.r.o., 2002. 238 stran, ISBN 80-214-2037-5.
- [21] JALURIA, Yogest a Kenneth E. TORRANCE. Computational Heat Transfer: series in computational and physical processes in mechanics and thermal sciences. 2. vydání. 29 West 35th Street New York NY 10001: Taylor & Francis, 2003. 2. edice, TJ260 .J35 2002. ISBN 1-56032-477-5.
- [22] IDĚLČIK, Issac Evsejevic, Snastina, A. A., Suchodolova, Ž. Michajlova, A., J. Bystrickaja, V. Spravočnik po gidravličeskim soprotivlenijam. 1. vyd. Moskva: Mašinostrajenie, 22/XI 1974, 558 s. T-10241.
- [23] KOLÁŘ, Václav, VINOPAL, Stanislav. Hydraulika průmyslových armatur: Příručka praktických výpočtů. 1. vyd. Praha 1: Státní nakladatelství technické literatury, 1963, 652 s. Strojírenská literatura. ISBN 04-101-63.
- [24] METZGER, M. Modelling and simulation of transient states. Příspěvek z konference Systems, Man and Cybernetics, 1993. “Systems Engineering in the Service of Humans”, Conference Proceedings., z 17.–20. října 1993, dostupný z http://80.ieeexplore.ieee.org.dialog.cvut.cz/stamp/stamp.jsp?tp=&arnumber=390838
- [25] WANG, Meiping; The Analysis of Operation Regulation Based on Origin in the central Heating system, 2011, vydáno ve sborníku z konference, Power and Energy Engineering Conference (APPEEC), 2011 Asia-Pacific, Wuhan, str. 1–4, ISSN 2157-4839, ISBN 978-1-4244-6253-7, článek dostupný z: http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=5748506&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D5748506
- [26] RAO, Achanta Ramakrishna; BIMLESH, Kumar; Friction Factor for Turbulent Pipe Flow, z 30. X. 2007, modifikovaný 19. IX. 2010, článek dostupný z: http://eprints.iisc.ernet.in/id/eprint/9587
- [27] BENONYSSON, Atli; BOHM, Benny; RAVN, Hanz; Energy Conversion and Management, 1996, Volume 36, Str. 297–314, článek dostupný z http://ac.els-cdn.com/019689049598895T/1-s2.0-019689049598895T-main.pdf?_tid=ab8b995cebb6abeda5da6cdc656b5b13&acdnat=1339690992_9f9c810cdd82da1038aa46339e89367b
- [28] KNEER, Aron; WIRTZ, M.; Development of an alternative cooling system (earth heat exchanger) for inverters of a solar plant, příspěvek z konference Star European conference, konané 22.–23. 3. 2011 v Noordviku, článek dostupný z http://www.tinnit.de/cms/download.php?cat=30_Umwelttechnik&file=Starconference_2011_earthcooling_tinnit.pdf
- [29] TZB-info, Katalog stavebních materiálů, dostupný z http://www.tzb-info.cz/docu/tabulky/0000/000068_katalog.html
- [30] MELICHAR, Jan; MOSLER, Pavel; Výchozí údaje pro projektování potrubí z termoplastů, Vodní hospodářství 7/2013, str. 223–226, článek dostupný z http://www.vodnihospodarstvi.cz/ArchivPDF/vh2013/vh07-2013.pdf
- [31] VESELSKÝ, Jaroslav; Local Head Loss in Polypropylene and Polyethylene Pipeline Joint Welded by Butt Fusion, článek dostupný z http://stc.fs.cvut.cz/pdf/VeselskyJaroslav-306611.pdf
- [32] MELICHAR, J.; HÁKOVÁ, J.; VESELSKÝ, J.; MICHLÍK, L.; Místní energetická ztráta spoje plastového potrubí, spojovaného svařováním na tupo, článek v časopise Vytápění, větrání, instalace. 2006, roč. 15, č. 1, s. 15–18. ISSN 1210-1389.
- [33] MELICHAR, J.; VESELSKÝ, J.; Místní energetická ztráta spoje polypropylénového a polyetylénového potrubí, zhotoveného svařováním na tupo, článek v časopise Vytápění, větrání, instalace. 2009, roč. 18, č. 1, s. 4–8. ISSN 1210-1389.
- [34] MELICHAR, Jan; MOSLER, Pavel; Determination of Pressure Loss in Plastic Pipeline, příspěvek z konference 15th International Freight Pipeline Society Symposium 2014 Czech Association of Scientific and Technical Societies (CSVTS), 24.–26. června 2014. Dostupné z http://stc.fs.cvut.cz/pdf13/2597.pdf
- [35] VARCHOLA, M.; KNÍŽAT, B.; TÓTH, P.; Hydraulické riešenie potrubných systémov, Vienala Košice, 2004, 265 str., ISBN 80-8073-126-8
Article freely continues the theme analysis of thermodynamic phenomena occurring in and around the pipeline construction, located in the loose backfill, now with respect to the theoretical foundations, describing hydraulic phenomena. The article includes in particular the currently known insight into the flow of transfer fluid steel hot water pipes, used in heating and author presents the calculated values of necessary input data for determining the hydraulic losses.