Reklama

Analýza termodynamických jevů v potrubních sítích II.

Teoretické základy – termomechanika, část 1/2

15.6.2015

Ing. Pavel Sláma

Recenzovaný

Článek volně pokračuje v tématu analýzy termodynamických jevů vyskytujících se uvnitř a v okolí potrubní konstrukce umístěné v sypkém zásypu, nyní s ohledem na teoretické základy popisující související jevy v oblasti sdílení tepla. Článek obsahuje především aktuálně známé vhledy do problematiky sdílení tepla v případě, kdy jsou tepelně izolované trubky umístěny poblíž sebe v zemním zásypu.

Reklama

Jednotlivé postupy směřující ke zhodnocení velikosti tepelných ztrát jsou použity ve vzorovém příkladu výpočtu konkrétní potrubní trasy, jejíž skutečný izolační stav byl předem ověřen měřením.

Termomechanika

Mechanismy sdílení tepla v potrubních rozvodech umístěných v homogenním zásypu

Měrnou tepelnou ztrátu, tedy velikost tepelného toku vycházejícího z jednotkového úseku potrubní trasy, je pro zhodnocení tepelně technických vlastností horkovodní soustavy vhodné trvale vyšetřovat pro přívodní i vratnou linii společně, protože při obvyklém uspořádání a parametrech tepelných sítí může docházet k trvalému či občasnému ovlivňování tepelných ztrát vzájemným působením obou potrubí uložených blízko sebe.

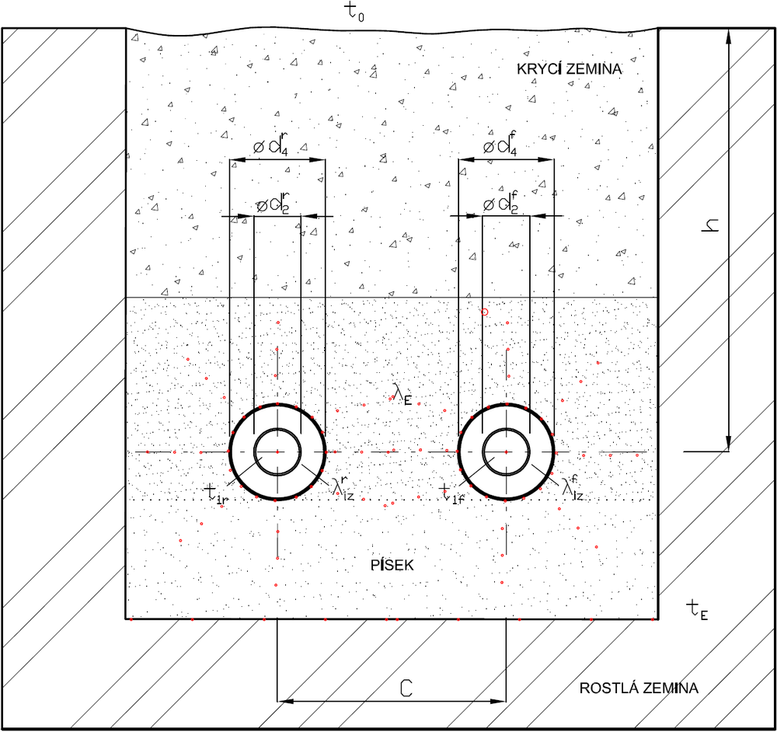
Tato celková celková tepelná ztráta je určována především následujícími veličinami (viz Obrázek 1)

Obrázek 1 – Řez dvoutrubní trasou v zemním zásypu

Osová hloubka potrubí: `h`

– souvisí s dovolenou minimální a s maximální možnou hloubkou krytí, která je dána především mechanickou odolností použité izolační hmoty a stavebně technickými předpisy platnými v místě montáže potrubí. Obecně lze uvést, že pro izolační materiály s mezí pevnosti v tlaku p_max ≤ 0,3 MPa, jako je např. tvrdá polyuretanová pěna, je tato osová hloubka v rozsahu h = (0,4 − ) až (2,5 − ) [m]

Vnitřní průměr izolačního pláště potrubí: `d`₂

– je dán vždy DN a výběrem materiálu medionosné trubky – je třeba vzít v úvahu, že tento rozměr může být i pro stejné DN a stejný tlakový stupeň u různých potrubí rozdílný. Tyto geometrické rozdíly se vyskytují např. mezi potrubím z běžných konstrukčních ocelí a potrubím z ocelí nerezových, stejně tak jako u potrubí sklolaminátových nebo u potrubí plastových. Spolehlivou informaci většinou poskytnou pouze katalogové listy jednotlivých výrobců.

Vnější průměr izolačního pláště: `d`₄

je v současnosti určen, za použití technologie předizolovaného potrubí, tzv. izolační třídou potrubí, související vždy s velikostí DN a tloušťkou a materiálem izolační vrstvy.

Tepelná vodivost izolačního materiálu: `λ`_iz

bude podrobně pojednána v dalších článcích této série, stejně tak jako i tepelná vodivost zásypového materiálu: λ_E

Dalšími veličinami ovlivňujícími tepelné procesy v okolí potrubí v zemním zásypu jsou:

Teplota topného média v přívodním potrubí: `t`_f

– tato hodnota je v naprosté většině tepelných sítí proměnná v čase a jedná se o primárně řízenou veličinu v soustavách zásobování teplem.

Teplota topného media ve vratném potrubí: `t`_r

– tato hodnota je hodnotou výslednou, hodnotou kontrolovanou, většinou však nikoliv přímo řízenou. Lze však předpokládat, že v následujících letech bude právě tato veličina přímo řízenou, a to za pomoci moderních třícestných armatur a zkratů zřízených v potrubních trasách a ve výměníkových stanicích.

Teplota povrchu země: `t`₀

– jedná se o poměrně snadno měřitelnou veličinu, proměnnou v čase, s možností alespoň částečné predikce.

Teplota zeminy ve vzdáleném okolí potrubní trasy: `t`_E

– v literatuře je uváděna standardní hodnota +8 °C, avšak již neplatná, přesto i v současnosti v technických výpočtech užívaná, výpočtová norma ČSN 06 0210 uvádí pro hloubky 1 až 2 m v topném období např. pro teplotu vzduchu −12 °C teplotu zeminy 0 °C.

Podle prací z Fakulty stavební ČVUT, Katedry technických zařízení budov, dostupných na stránkách katedry je možno uvažovat s tím, že teplota zeminy v hloubce 1 m kolísá v průběhu roku od 3 °C (leden) až do 18 °C (srpen).

Z těchto důvodů není možno uvažovat v přesném tepelně technickém výpočtu s touto hodnotou jako s konstantou a její přesnější průběh bude řešen dále.

Teoretické přístupy k vedení tepla v zemině

Teoretické řešení tepelných ztrát předizolovaného potrubí uloženého v pískovém a zemním zásypu je dosti obtížné a nikdy zcela nevystihuje skutečnost.

Anglosaská literatura, např. [1], i v případě potrubí uloženého v zásypu často pracuje s tvarovým faktorem tepelné vodivosti, tedy vychází ze základní Fourierovy rovnice prostupu tepla

kde je

A: – plocha kolmá na osu proudění tepla
λ: – součinitel tepelné vodivosti

a symbol i je vztažen ke i-té řadě, (viz Obrázek 2)

Obrázek 2 – Tepelný tok dle [1]

Z obrázku vyplývá, že tepelný tok je stejný při průchodu všemi hodnocenými buňkami o ploše ΔxL

Rovnice tepelného toku odráží předpoklad, že všechny průřezy buněk jsou o rozměru Δx • Δy. Další vyjádření pro celkový tepelný tok z vnitřního povrchu na vnější povrch podél řady je

kde N je celkové množství zakřivených ploch v jednotlivé řadě. Uvedené řešení předpokládá, že Δx ≈ Δy

Tato rovnice může být napsána pro každý vyšetřovaný tok tepla. Jestliže máme M toků tepla, obdržíme pro zmíněný předpoklad, že Δx ≈ Δy, celkový tepelný tok

Obecně lze pak napsat

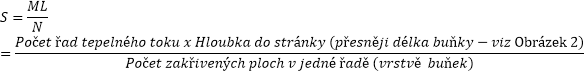
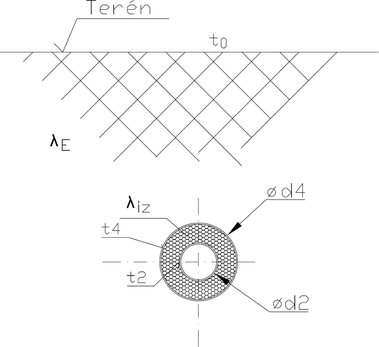
Obrázek 3 – ocelové izolované potrubí KMR kruhového průřezu

Jestliže provedeme podle této metodiky posouzení průniku tepla válcovou plochou, viz Obrázek 3, kde tepelná ztráta je

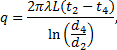
tak hodnota je právě tímto tvarovým faktorem. Podobným způsobem pak je tvarový faktor tepelné vodivosti získáván pro další tvary.

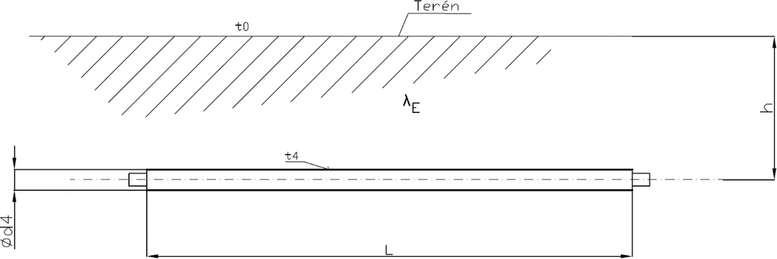
Obrázek 4 – Izolované potrubí v zemním zásypu

Pro potrubí v zásypu, kde hloubka zásypu h je podstatně větší než vnější průměr zasypané trubky d₄, viz Obrázek 4, a i délka L vyšetřovaného potrubí je podstatně větší než hloubka zásypu h, je tvarový faktor dle [1]

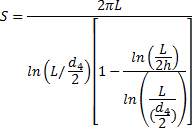
a tepelný tok

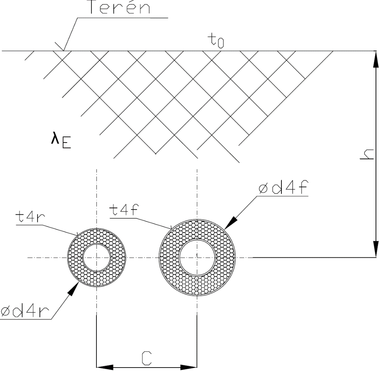
Obrázek 5 – Dvě potrubí v zemním zásypu pro hodnocení tepelné směny probíhající mezi nimi

Vzájemnou tepelnou směnu mezi dvěma potrubími zasypanými v nekonečném zemním zásypu, viz Obrázek 5, je možno vyjádřit za pomoci tvarového faktoru také. Pro dvě válcová potrubí zasypaná v nekonečném zemním zásypu je tvarový faktor dle [1]

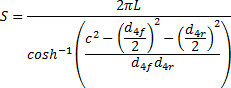
i zde však platí podmínka, že délka potrubí L musí být podstatně větší než vnější průměr obou trubek, ev. vnější průměr d₄ obou posuzovaných potrubí. Stejně tak musí být tato délka potrubí L podstatně větší než vzdálenost mezi osami obou trubek C.

Dle [13] může být pro vyšetření poměrů a vzájemných vazeb přínosem metoda skládání polí. Jsou-li v tělese soustředěny zdroje a odběry tepla, které lze popsat lineárními diferenciálními rovnicemi, a okrajové podmínky sdílení tepla jsou též lineární, jsou jednotlivá teplotní pole vytvořená zdroji a odběry tepla vzájemně nezávislá. Výsledné teplotní pole je pak součtem jednotlivých teplotních polí.

Základem výpočtu jsou fiktivní zdroje a fiktivní odběry tepla. Zdrojem tepla je trubka uložená v zemi, fiktivním odběrem tepla je zrcadlově umístěný energetický propad energie v prostoru nad zemí v místě M2 – viz Obrázek 6.

Obrázek 6 – Schéma řešení trubky uložené v zemi – převzato a upraveno dle [13]

Do poloprostoru řešené úlohy – v tomto případě je to země – je uloženo v osové hloubce h potrubí o vnějším průměru d₄. Na povrchu trubní konstrukce je teplota t₄ a na povrchu teplota země t_o. To znamená, že povrch musí být intenzivně ochlazován přirozeným prouděním vzduchu v přízemních vrstvách, jinak by teplota povrchu země poblíž potrubí byla vyšší než teplota povrchu země ve větší vzdálenosti od lokality, kde je potrubí uloženo.

V souladu s platnými fyzikálními zákony je trubka nahrazena jednorozměrným zdrojem tepla se stejnou mohutností +q (W/m) jako je tepelné ztráta sdružené trubní konstrukce. Tento zdroj je zobrazen na obrázku jako M1, který neleží v ose potrubí.

V druhém poloprostoru, zrcadlově vůči povrchu země, je zaveden v bodu M2 energetický propad o mohutnosti −q s tím, že platí l − ql = l + ql.

Izoterma t_o rozděluje oba poloprostory a představuje přibližně povrch země.

Izotermické plochy nezávislých polí zdroje a odběru tepla budou mít tvar soustředných válcových ploch kolem os procházejících body M1 a M2 kolmo k nákresně. V obrázku se tyto izotermické plochy zobrazují jako kružnice značené např. pro zvolený bod P hodnotami t´a t´´, s poloměry r´a r´´.

Podle výsledného tvaru Fourierova zákona pro vedení tepla válcovou stěnou platí pro izotermickou plochu zdroje

a pro izotermickou plochu odběru

kde je

λ_E: – součinitel tepelné vodivosti země
y_o: – vzdálenost zdroje či propadu měřená na normále k povrchu země
r´, r´´: – poloměry (průvodiče zvoleného bodu P z bodů M1 a M2).

Po součtu obou předchozích rovnic získáme pro obecný bod

Jestliže umístíme počátek souřadnic do průsečíku svislé osy sdružené trubní konstrukce s povrchem země, tedy do poloviny vzdálenosti bodů M1 a M2, bude možno vyjádřit poloměr a a tedy

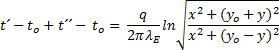
Pro symetrické uspořádání t_o = 0, a kdy součet t´ + t´´ udává výslednou teplotu t, je konečný tvar teploty v daném místě souřadného systému určen rovnicí

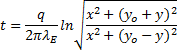
Z podoby výsledné rovnice je patrné, že výsledné izotermy uvnitř vyšetřované plochy (prostoru) mají tvar kružnic, jejichž střed se pohybuje dolů od bodu M1 tak, jak klesá teplota v příslušné vzdálenosti.

Pro další postup je třeba získat pokud možno přesnou hodnotu vzdálenosti zdroje a odběru tepla od počátku svislé osy souřadného systému, tedy od povrchu země +y_o a −y_o.

Povrch potrubí je válcový a při velikostech vnějšího krycího pláště izolace o světlosti přibližně 200 mm je možno průběh teploty na jeho povrchu ztotožnit s izotermou t₄. Pro všechny body na této izotermě platí, že q = konst. a pro libovolné dva body na izotermě t₁ , i např. body K a N (viz Obrázek 6), musí platit

Tedy pak pro body K a T (viz Obrázek 6) platí

a následně

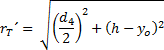
Obrázek 7 – Schéma řešení trubky uložené v zemi – převzato a upraveno dle [13]

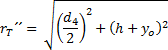
Po dosazení a řešení je

Pro body (K a N, x = 0) izotermy t₁ platí

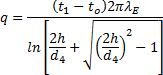
Publikace [13] uvádí jako převzatý i následující vzorec

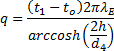
Pro dvě tepelně izolované trubky, viz Obrázek 7, je možno dle [13] použít, a to při zanedbání tepelného odporu vznikajícího při přestupu mezi proudící teplonosnou látkou, tepelného odporu samotné médionosné ocelové trubky, které oba jsou, jak bude prokázáno v dalších pokračováních tohoto článku, zcela minimální, pro získání hodnoty tepelného odporu přívodní trubky R_f, vzorec

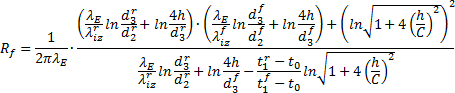
a pro získání tepelného odporu potrubí vratného vzorec

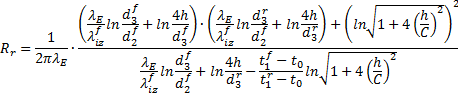
Uvedený vzorec nepočítá s izolačním odporem HDPE izolačního pláště o tloušťce 3 mm.

Odpor tohoto izolačního pláště pro přívodní potrubí je

a stejně tak pro potrubí vratné

Tyto, pouze úplnost uvedené tepelné odpory izolačního pláště, nebývají ve vztahu k tepelnému odporu PUR izolační hmoty a především vzhledem k tomu, že tepelné vodivosti λ_c / λ_iz > 10 a současně i tloušťky izolačních vrstev s_c / s_iz > 10, významné a do praktického výpočtu se obvykle nezapočítávají.

Měrná tepelná ztráta přívodní trubky pak je

a trubky vratné

Celková tepelná ztráta obou potrubí je součtem těchto jednotlivých měrných tepelných ztrát:

V posledních letech se objevují, převážně ve Skandinávii, i další nové výpočtové metody tepelných ztrát vyvíjené pro použití v programech, jako je např. Fluent.

Druhá část tohoto článku obsahuje výpočet na konkrétním příkladu z praxe, na kterém jsou patrné rozdíly v jednotlivých výpočtových postupech.

Seznam použitých symbolů a zkratek

Tabulka 1 – Seznam použitých symbolů
označení v textu	význam	jednotka
`T`	absolutní teplota	K
`t`	teplota	°C
`ς`	měrná hmotnost	kg/m³
`λ`	součinitel tepelné vodivosti	W/mK
`L`	délka	m
d	průměr	m
`R`	tepelný odpor konstrukce	mK/W
`Q`	tepelný tok	W
`p`	tlak	Pa
`q`	měrný tepelný tok vztažený k jednotce délky či plochy	W/m [W/m²]
`C`	osová rozteč	m
`A`	plocha kolmá ke směru tepelného toku	m²
`S`	tvarový faktor	[–]
`s`	tloušťka izolační vrstvy	m
`r`	poloměr	m
`α`	součinitel přestupu tepla	[W/m²K]
`h`	osová hloubka	m
`G`	celková tepelná vodivost trubní konstrukce	W/mK

Tabulka 2 – Seznam použitých zkratek
zkratka	plný význam
DN	„Diameter nominal“ – jedná se o označení určující přibližně velikost příslušných součástí potrubí a to zpravidla ve vztahu k jejich skutečnému vnitřnímu průměru
CZT	Centralizované zásobování teplem
SCZT	Soustava centralizovaného zásobování teplem
KMR	Sdružená potrubní předizolovaná konstrukce tvořená medionosnou trubkou, izolací a povrchovou krycí trubkou se vzájemnými pevnými mechanickými vazbami
TV	Teplá voda, ohřátá pitná voda

English Synopsis

Thermodynamic effects in the pipeline and its surroundings – Theoretical basis – thermomechanics. Part 1/2

Article freely continues the theme of thermodynamic analysis of phenomena occurring in and around the pipeline construction, located in the sandy backfill, now with respect to theoretical foundations, describing the related effects of heat transfer. The article includes in particular the currently known insights into heat exchange in the case where the thermally insulated pipes placed near each other in the soil backfill. Individual processes intended to evaluate size of heat loss are used in the model calculation example a specific pipeline, whose real insulating state has previously been verified by measurement.