Model a dimenzování solárního komínu jako progresivního systému na podporu přirozeného větrání budov
Vytvoření teoretického modelu solárního komínu si klade za cíl popsat základní aspekty, které ovlivňují jeho kvantitativní funkci v reálných podmínkách. Úvodem je však třeba zdůraznit, že tento zápis vycházející z dodržování základních fyzikálních principů není definitivní a jedinou verzí návrhu takového systému.
Režim solárneho komína možno v zásade rozdeliť na denný a nočný. V rámci oboch môže nastať stav bezvetria, keď je pohyb vzduchu solárnym komínom vyvolaný vztlakom na základe rozdielu teplôt vzduchu medzi interiérom a exteriérom, alebo opačný stav, keď je pohyb vzduchu solárnym komínom vyvolaný vztlakom z teplotného rozdielu vzduchu medzi vnútorným a vonkajším prostredím v kombinácii s dynamickým účinkom vetra.
V čase bezvetria využíva solárny komín potenciál priameho slnečného žiarenia na dosiahnutie vyššej teploty vzduchu, ktorý následne stúpa smerom nahor v dôsledku nižšej objemovej hmotnosti. V opačnom prípade - pri veterných podmienkach - sa na pohybe vzduchu solárnym komínom podieľa okrem slnečného žiarenia aj dynamický účinok vetra. Na využitie potenciálu slnečnej energie je súčasťou konštrukcie solárneho komína jeho transparentný kryt, orientovaný južným smerom, z ktorého možno získať maximálne solárne energetické zisky. Absorpciou slnečného žiarenia vnútornými povrchmi po prechode transparentnou časťou dochádza k zložitým tepelným procesom medzi jednotlivými časťami solárneho komína a okolia, ktoré pozostávajú z kondukcie, konvekcie, radiácie tepla a jej celkovej transmisie. Na účely teoretického modelu návrhu solárneho komína sa preto prijal predpoklad, že teplo privedené absorbovaným slnečným žiarením, zmenšené o teplo odvedené do okolia, sa rovná teplu odovzdanému vzduchu, ktorý prúdi šachtou solárneho komína.
Základné vzťahy matematicko-fyzikálneho modelu solárneho komína
Teplota vzduchu na výstupe zo solárneho komína pri pôsobení priameho slnečného žiarenia (obr. 1) sa vypočíta ako
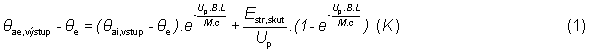
θae, výstup - teplota vzduchu na výstupe zo solárneho komína (°C),
θai, vstup - teplota vzduchu na vstupe do solárneho komína (°C),
θe - stredná vonkajšia teplota vzduchu v čase slnečného svitu (°C),
Estr, skut - skutočná stredná slnečná ožiarenosť za zasklením (W/(m2 . deň)),
Up - priemerný váhový koeficient prechodu tepla konštrukciou solárneho komína (W/(m2 . K)),
B - efektívna šírka kolekčnej plochy solárneho komína (m),
L - efektívna výška kolekčnej plochy solárneho komína (m),
M - hmotnostný prietok vzduchu solárnym komínom (kg/s),
c - merná tepelná kapacita vzduchu (J/(kg . K)).

Obr. 1 Teplotný režim solárneho komína
Legenda k obr. 1:
1 - stredná vonkajšia teplota vzduchu θe v čase slnečného svitu (°C),
2 - teplota vzduchu θai, vstup na vstupe do solárneho komína (°C),
3 - teplota vzduchu θae, výstup na výstupe zo solárneho komína (°C)
Na základe toho možno vypočítať vzostup teploty vzduchu medzi jeho vstupom do solárneho komína a jeho výstupom zo solárneho komína ako
![]()
Δθ - rozdiel teplôt vzduchu po výške solárneho komína (°C),
θae, výstup - teplota vzduchu na výstupe zo solárneho komína (°C),
θai, vstup - teplota vzduchu na vstupe do solárneho komína (°C).
Na určenie hodnoty priemerného váhového koeficientu prechodu tepla (konštrukciou solárneho komína) je nevyhnutné poznať vopred materiálovo-konštrukčné riešenie solárneho komína (obr. 2, 3), najmä tepelno-technické vlastnosti použitých stavebných materiálov. Platí, že
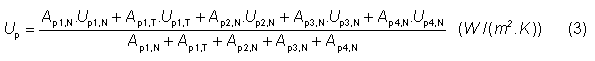
Up - priemerný váhový koeficient prechodu tepla konštrukciou solárneho komína (W/(m2 . K)),
Up1, N, Up1, T, Up2, N, Up3, N, Up4, N - parciálny súčiniteľ prechodu tepla príslušnou časťou solárneho komína (W/(m2 . K)),
Ap1, N, Ap1, T, Ap2, N, Ap3, N, Ap4, N - plocha príslušnej časti solárneho komína (m2).
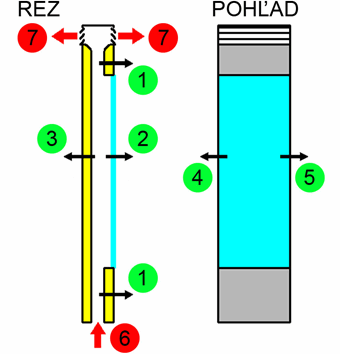
Obr. 2 Schéma solárneho komína - zvislý rez a pohľad
Legenda k obr. 2:
1 - plocha Ap1, N (m2) a súčiniteľ prechodu tepla Up1, N (W/(m2 . K)),
2 - plocha Ap1, T (m2) a súčiniteľ prechodu tepla Up1, T (W/(m2 . K)),
3 - plocha Ap2, N (m2) a súčiniteľ prechodu tepla Up2, N (W/(m2 . K)),
4 - plocha Ap3, N (m2) a súčiniteľ prechodu tepla Up3, N (W/(m2 . K)),
5 - plocha Ap4, N (m2) a súčiniteľ prechodu tepla Up4, N (W/(m2 . K)),
6 - vstup vzduchového prúdu do solárneho komína,
7 - výstup vzduchového prúdu zo solárneho komína

Obr. 3 Schéma solárneho komína - priečne rezy
Legenda k obr. 3:
1 - plocha Ap1, N (m2) a súčiniteľ prechodu tepla Up1, N (W/(m2 . K)),
2 - plocha Ap1, T (m2) a súčiniteľ prechodu tepla Up1, T (W/(m2 . K)),
3 - plocha Ap2, N (m2) a súčiniteľ prechodu tepla Up2, N (W/(m2 . K)),
4 - plocha Ap3, N (m2) a súčiniteľ prechodu tepla Up3, N (W/(m2 . K)),
5 - plocha Ap4, N (m2) a súčiniteľ prechodu tepla Up4, N (W/(m2 . K)),
8 - vzduchový kanál solárneho komína na prúdenie vzduchu
Slnečné žiarenie prenikajúce transparentnou časťou solárneho komína spôsobuje vzostup teploty vzduchu (obr. 1). Vplyvom teplotného rozdielu vzduchu medzi jeho prívodom do miestnosti a výstupom zo solárneho komína dochádza k vzniku prirodzeného vztlaku, ktorý vyvoláva prirodzený pohyb (prúdenie) vzduchu. S týmto stavom sa počíta v prípade bezveterných podmienok a pri stanovovaní účinného vztlaku z rozdielu teplôt po výške H sa vychádza z lineárneho priebehu teplôt. Určujúcimi fyzikálnymi veličinami sú teplota a hustota vzduchu v ťažisku pravouhlého trojuholníka (4). Lineárny priebeh teploty vzduchu je aproximáciou skutočného priebehu teplôt po výške H (obr. 4).

Obr. 4 Aerodynamický režim solárneho komína - aproximácia priebehu teplôt vzduchu po efektívnej výške H na vznik prirodzeného vztlaku z rozdielu teplôt
Legenda k obr. 4:
1 - stredná vonkajšia teplota vzduchu θe v čase slnečného svitu (°C),
2 - teplota vzduchu θi, vstup na vstupe do solárneho komína (°C),
3 - teplota vzduchu θae, výstup na výstupe zo solárneho komína (°C)
Pri veterných podmienkach sa započítava do hodnoty účinného vztlaku aj dynamický účinok vetra (5). Vplyv vetra pri danej rýchlosti sa zohľadňuje výsledným tlakovým koeficientom Cp., ktorého hodnotu možno získať z literatúry. Na získanie presnejších údajov či priamo pre konkrétne prípady možno vykonať analýzu v aerodynamickom tuneli alebo využiť simulačné programy CFD.

ΔpT - účinný vztlak z rozdielu teplôt (Pa),
ΔpT, W - účinný vztlak z rozdielu teplôt a dynamického účinku vetra (Pa),
S(H, ΔθH) - plocha pravouhlého trojuholníka aproximovaného priebehu teploty vzduchu (m2), pričom platí S(H, ΔθH) = 0,5 .H . (θae,výstup - θe) (m2),
g - gravitačné zrýchlenie (m/s2),
ρťažisko - hustota vzduchu pri teplote θťažisko (kg/m3),
θťažisko - teplota vzduchu odpovedajúca ťažisku aproximovanej plochy S(H,ΔθH) (°C),
H - efektívna výška na vznik prirodzeného vztlaku z rozdielu teplôt (m),
ΔθH - rozdiel teplôt vzduchu po efektívnej výške na vznik prirodzeného vztlaku (°C),
θe - stredná vonkajšia teplota vzduchu v čase slnečného svitu (°C),
θae, výstup - teplota vzduchu na výstupe zo solárneho komína (°C),
Cp - výsledný tlakový koeficient (-),
ρw - hustota vetra (kg/m3),
ww - rýchlosť vetra (m/s).
Samozrejme, do úvahy treba brať aj odporové faktory, ktorými sú miestne aerodynamické odpory a aerodynamický odpor vznikajúci trením tekutiny (vzduchu) o steny potrubia. Medzi miestne aerodynamické odpory sa radí napríklad zmena prierezu potrubia alebo zmena smeru vedenia potrubia.
Dimenzovanie solárneho komína
Metodiku dimenzovania solárneho komína možno v skrátenej podobe zhrnúť do niekoľkých nasledujúcich krokov:
Krok č. 1 - stanovenie požadovanej výmeny vzduchu v miestnosti
Na úvod treba určiť požadovanú výmenu vzduchu v miestnosti, t. j. hmotnostný prietok vzduchu, ktorý sa bude označovať vo výpočtoch ako výpočtový hmotnostný prietok vzduchu Mvýpočtový. Keďže materiálovo-konštrukčné riešenie solárneho komína je vopred dané, možno vypočítať priemerný váhový súčiniteľ prechodu tepla Up, podľa vzťahu (3).
Krok č. 2 - stanovenie teploty vzduchu na výstupe zo solárneho komína
Na základe vytvoreného modelu o vonkajšej klíme (teplota vonkajšieho vzduchu v čase slnečného svitu, skutočná stredná slnečná ožiarenosť v danej lokalite) sa podľa vzťahu (1) určí teplota vzduchu na výstupe zo solárneho komína θae, výstup. Táto hodnota sa stanovuje pri hmotnostnom prietoku vzduchu označovanom v 1. kroku ako výpočtový hmotnostný prietok vzduchu Mvýpočtový.
Krok č. 3 - stanovenie účinného vztlaku
Ak sa predpokladá stav bezvetria, vypočíta sa hodnota prirodzeného vztlaku iba z rozdielu teplôt po výške H, t. j. podľa vzťahu (4). V prípade, že pohyb vetra nie je zanedbateľný, postupuje sa podľa vzťahu (5), takže sa zohľadní vplyv vetra a jeho dynamický účinok na tlakové pomery vo vnútri miestnosti, ako aj v okolí samotnej stavby. Na toto je vhodné pri danom stavebnom riešení určiť hodnotu výsledného tlakového koeficientu Cp, napríklad použitím výpočtových simulačných programov pre CFD, modelovaním stavby vrátane okolitej blízkej zástavby v aerodynamickom tuneli, alebo orientačne pomocou tabuľkových hodnôt z literatúry.
Krok č. 4 - stanovenie skutočného hmotnostného prietoku vzduchu
Ako sme už spomínali, pri dimenzovaní solárneho komína treba počítať aj s odporovými faktormi, ktoré vznikajú pri prúdení vzduchu kanálom solárneho komína. Veľkosť odporových faktorov je daná geometriou solárneho komína, vstupnými a výstupnými otvormi na prívod a odvod vzduchu, ako aj vlastnosťami použitých materiálov, najmä drsnosťou povrchu. Z tohto dôvodu sa bude na účely stanovenia hodnoty skutočného hmotnostného prietoku vzduchu Mskutočné predpokladať rovnosť medzi účinným vztlakom a celkovým aerodynamickým odporom solárneho komína podľa vzťahov (6) a (7).
Zavedieme aj pojem predpokladanej hodnoty koeficienta celkového aerodynamického odporu s označením Zpredpoklad a orientačne určíme jeho hodnotu. Na základe takéhoto postupu sa z rovnosti medzi účinným vztlakom a celkovým aerodynamickým odporom solárneho komína vypočíta podľa vzťahov (8) a (9) rýchlosť prúdenia vzduchu w a následne aj skutočný hmotnostný prietok vzduchu Mskutočné. Ak sa prietoková plocha po výške solárneho komína mení, treba počítať do vzťahov (8) a (9) s hodnotou stanovenou váženým priemerom.

ΔpT - účinný vztlak z rozdielu teplôt (Pa),
ΔpT, W - účinný vztlak z rozdielu teplôt a dynamického účinku vetra (Pa),
ΔpTS - celkový aerodynamický odpor solárneho komína - tlak spotrebovaný na urýchlenie prúdu vzduchu a prekonanie hydraulických odporov (Pa),
Zpredpoklad - predpokladaná hodnota koeficienta celkového aerodynamického odporu po pohybovej línii vzduchu (-),
ρťažisko - hustota vzduchu pri teplote θťažisko (kg/m3),
w - priemerná rýchlosť prúdenia vzduchu (m/s),
Mskutočný - skutočný hmotnostný prietok vzduchu (kg/s),
S - prietoková plocha solárneho komína (vnútorný prierez) (m2).
Iteratívny postup
Postupnosť krokov 1 až 4 treba opakovať až dovtedy, kým sa nedosiahne zhoda medzi hodnotou výpočtového hmotnostného prietoku vzduchu Mvýpočtový a skutočným hmotnostným prietokom vzduchu Mskutočný pri predpokladanej hodnote koeficienta celkového aerodynamického odporu Zpredpoklad.
Overenie hodnoty skutočného hmotnostného prietoku vzduchu
Keďže hodnota koeficienta celkového aerodynamického odporu Zpredpoklad sa na účely stanovenia skutočného hmotnostného prietoku vzduchu solárnym komínom iba predpokladala, je nevyhnutné ju porovnať ju na záver so skutočnou hodnotou koeficienta celkového aerodynamického odporu Zskutočné. Na to treba spracovať detailnú analýzu kvantifikácie aerodynamického koeficienta trením tekutiny a miestnych odporov po pohybovej línii vzduchu. Podľa vzťahu (10) platí, že ak bude hodnota Zskutočné menšia ako Zpredpoklad, možno tvrdiť, že hodnota skutočného hmotnostného prietoku vzduchu solárnym komínom sa dosiahne pri daných okrajových podmienkach uvažovaných vo výpočte.
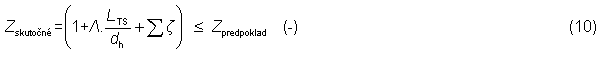
Zskutočné - skutočná vypočítaná hodnota koeficienta celkového aerodynamického odporu po pohybovej línii vzduchu (-),
Zpredpodklad - predpokladaná hodnota koeficienta celkového aerodynamického odporu po pohybovej línii vzduchu (-),
Λskutočné - súčiniteľ trenia (-),
LTS - celková dĺžka vzduchového kanála solárneho komína po pohybovej línii vzduchu (m),
dh - hydraulický priemer vzduchového kanála solárneho komína (m),
Σζ - suma aerodynamických koeficientov miestnych odporov (-).
V budúcnosti vám na stránkach časopisu TZB Haustechnik priblížime výsledky z analýzy solárneho komína, inštalovaného na Fakulte strojného inžinierstva VUT v Brne.
Foto a obrázky: archív autorov, Ing. Pavel Charvát, PhD.
Príspevok vznikol v rámci projektu ITMS 26220120018 - Podpora Centra excelentného integrovaného výskumu progresívnych stavebných konštrukcií, materiálov a technológií.
Literatúra
1. CIHELKA, J.: Solární tepelní technika. Praha: T. Malina, 1994. 208 s.
2. BIELEK, B., BIELEK, M., PALKO, M.: Dvojité transparentné fasády budov, 1. diel. Bratislava: Coreal, 2002.206 s.
3. BIELEK, B., BIELEK, M., KUSÝ, M., PAŇÁK, P.: Dvojité transparentné fasády budov, 2. diel. Bratislava: Coreal, 2002. 251 s.
4. JUREČKA, P.: Proudění a sdílení tepla. (Cvičení do předmětu Sdílení tepla a proudění). Ostrava: VŠB - Technická univerzita Ostrava, 2006. 129 s.
5. RECKNAGEL, SPRENGER, SCHRAMEK: Taschenbuch für Heizung und Klimatechnik. München: Oldenbourg Verlag GmbH, 1995. 1 865 s.
6. KOVÁČ, M.: Energetické toky v budovách vo väzbe na navrhovanie progresívnych sústav techniky prostredia. (Písomný referát k dizertačnej skúške). Košice: Svf TUKE, 2009.
Creating a theoretical model of the solar chimney aims to describe fundamental aspects that affect its function in quantitative real conditions. First, it must be emphasized that this record based on fundamental physical principles is not final and only draft versions of the system.