Hluk ve vzduchotechnice (I) - Základní pojmy a praktické vztahy
Zvuk se může šířit v plynech, kapalinách i pevných látkách. U plynů a kapalin se jedná o podélné akustické vlnění, které je charakterizováno zhušťováním a zřeďováním prostředí ve kterém se šíří. Akustické vlnění postupuje od zdroje zvuku ve vlnoplochách.
Vlnoplocha se vyznačuje tím, že v jejích všech bodech je v daném časovém okamžiku stejný akustický stav (míra zhuštění). Kolmice na vlnoplochu se nazývá akustickým paprskem.
Vlnová délka je vzdálenost mezi dvěma nejbližšími body na akustickém paprsku, které mají stejný akustický stav. Jinak lze říci, že je to vzdálenost, kterou zvuková vlna urazí za dobu jednoho kmitu T.
Převrácená hodnota doby kmitu T je frekvence (kmitočet). Označujeme ji f a jednotkou je hertz (Hz). Určuje počet kmitů za sekundu, které vykoná hmotný bod prostředí v němž se vlna šíří.
| Platí: | l . f = c | (1.1) |
kde c je rychlost šíření zvuku. Ve vzduchu je c = 340 m/s a pak pro představu vycházejí následující vlnové délky
| f = | 100 Hz | 1 000 Hz | 10 000 Hz |
| l= | 3,4 m | 0,34 m | 0,034 m |
Se zhušťováním a zřeďováním částic souvisí změny celkového statického tlaku. Barometrický tlak je hodnota přibližně 100 000 Pa. Akustický tlak se k tomuto tlaku přičítá. Je však o mnoho řádů nižší. Lidské ucho začíná vnímat akustické tlaky od hodnot 2.10-5 Pa, což je hodnota téměř zanedbatelná.
Šíření zvuku je spojeno s přenosem energie. Zdroj hluku je jednoznačně charakterizován akustickým výkonem LP (W).
Intenzita zvuku I (W/ m2) je akustický výkon procházející 1 m2 vlnoplochy.
Tyto akustické veličiny se v praxi mění o mnoho řádů. Proto byl v technické akustice zaveden pojem „hladin“ jednotlivých akustických veličin, jejichž veličinou je „decibel“.
Hladina akustického výkonu je definována vztahem
| LW = 10 log (W/Wo) | (1.2) |
kde W0 je referenční hodnota a úmluvami ISO byla stanovena na 10-12 W
Hladina akustického tlaku je definována vztahem
| Lp = 20 log (p/po) |
(1.3) |
kde po je referenční hodnota 2 . 10-5 Pa
Vhodnost decibelové stupnice dokazují následující příklady.
| (W) | (dB) | |||
|
Vyzářený akustický výkon |
106 | 180 | velký raketový motor | |
| 105 | 170 | vojenský proudový motor | ||
| 104 | 160 | čtyřmotorový vrtulový letoun | ||
| 103 | 150 | |||
| 102 | 140 | 75 členný orchestr | ||
| 10 | 130 | velká sbíječka | ||
| 1 | 120 | klavír | ||
| 10–1 | 110 | automobil na dálnici | ||
| 10–2 | 100 | tkalcovský stav | ||
| 10–3 | 90 | axiální ventilátor (50 m3/s); křičící člověk | ||
| 10–4 | 80 | vysavač | ||
| 10–5 | 70 | běžně mluvící člověk | ||
| 10–6 | 60 | malý ventilátor | ||
| 10–7 | 50 | |||
| 10–8 | 40 | velmi tichý šepot | ||
| 10–9 | 30 |
| (1) | - | Vyzařovaný akustický výkon, obvyklý způsob psaní | - P (W) |
| (2) | - | Dtto, ale exponenciální notace | - P (W) |
| (3) | - | Hladina akustického výkonu při ref. hodnotě 1 W | - LW (dB) |
| (4) | - | Hladina akustického výkonu při ref. hodnotě 10 -12 W | - LW (dB) |
|
|
||||
| (1) | (2) | (3) | (4) | |
| 100 000 | 10 5 | 50 | 170 | |
| 10 000 | 10 4 | 40 | 160 | |
| 1 000 | 10 3 | 30 | 150 | |
| 1 000 | 10 3 | 30 | 150 | |
| 100 | 10 2 | 20 | 140 | |
| 10 | 10 1 | 10 | 130 | |
| 1 | 1 | 0 | 120 | |
| 0 | ,1 | 10-1 | -10 | 110 |
| 0 | ,01 | 10-2 | -20 | 100 |
| 0 | ,001 | 10-3 | -30 | 90 |
| 0 | ,000 1 | 10-4 | -40 | 80 |
| 0 | ,000 01 | 10-5 | -50 | 70 |
| 0 | ,000 001 | 10-6 | -60 | 60 |
| 0 | ,000 000 1 | 10-7 | -70 | 50 |
| 0 | ,000 000 01 | 10-8 | -80 | 40 |
| 0 | ,000 000 001 | 10-9 | -90 | 30 |
S hlukoměry měříme akustický tlak – hladiny akustického tlaku:
| (mPa) | (dB) | |
| 140 | ||
| 108 | Hluk v blízkosti letadla | |
| 120 | ||
| 107 | Práce s pneumatickým kladivem | |
| 100 | ||
| 106 | Jízda autem | |
| 80 | ||
| 105 | Kancelář | |
| 60 | ||
| 104 | Tichý byt | |
| 40 | ||
| 103 | Tichý les | |
| 20 | ||
| 102 | ||
| 10 | ||
| 20 | Práh slyšení | |
| 0 |
Hluk v praxi se skládá ze zvuků o různých vlnových délkách (různých frekvencí). Abychom mohli hluk posuzovat, zjišťovat jeho složení a účinky, bylo zavedeno jeho hodnocení v oktávových frekvenčních pásmech. Normou ČSN 356870 byly stanoveny střední kmitočty v jednotlivých oktávových pásmech a to od 16 do 16000 Hz. Ve vzduchotechnice pracujeme obvykle s hodnotami v osmi oktávách:
63 125 250 500 1000 2000 4000 8000 (Hz)
Frekvenční pásmo o šířce jedné oktávy je charakterizováno tím, že poměr krajních frekvencí je dvě.
f2 / f1 = 2
Střední frekvence, kterou je oktáva označována, je určena vztahem
fstr = Ö ( f1 . f2)
Krajní hodnoty pásma určíme ze vztahů
f1 = fstr / Ö 2 a f2 = fstr . Ö 2
Při sčítání několika zvuků získáme výsledný akustický tlak podle vztahu
p = Ö (p12 + p22 + ………+pn2 )
Pracujeme-li s hladinami L1 až Ln je výsledná hladina dána
| L = 10 log ( 100,1L1 + 100,1L2 + ……+ 100,1L n ) | (1.4) |
Například sečteme-li dvě stejné hladiny, dostaneme hladinu o 3 dB vyšší.
S ohledem na ochranu sluchu, účinné dorozumívání a únavu člověka byly stanoveny normou ISO třídy hluku, které stanovují maximální hladiny pro jednotlivá frekvenční pásma.
Třída hluku N je dána vztahem
L = a + bN
| f (Hz) | 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 |
| a | 35.5 | 22.0 | 12.0 | 4.8 | 0 | -3.5 | -6.1 | -8.0 |
| b | 0.790 | 0.870 | 0.930 | 0.974 | 1 | 1.015 | 1.025 | 1.030 |
Graf je uveden na obr. 1.
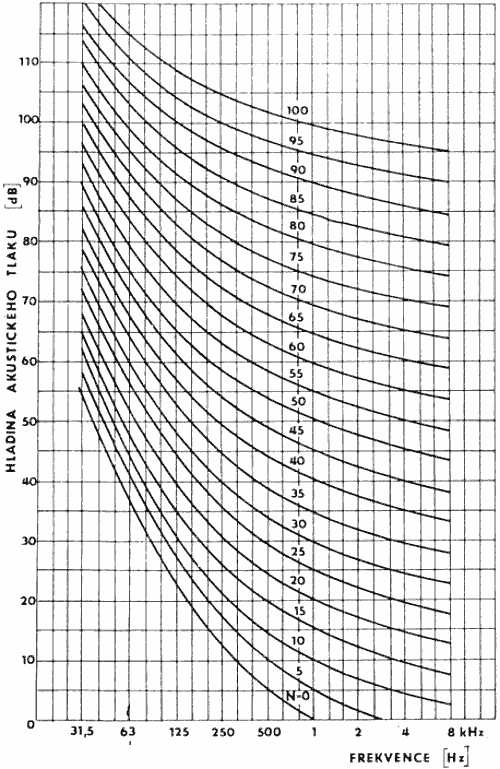
Obr. 1 – Třídy hluku N dle ISO
Vyneseme-li spektrum hluku do tohoto grafu je hluk té třídy N (výsledné), která odpovídá nejvýše položené čáře N, ještě se dotýkající zadaného spektra hluku.
To je důležité v praxi pro řešení útlumu hluku. Musíme tlumit především ty frekvence, které způsobují zvýšení třídy hluku.
V praxi se pro hodnocení hluku často používá hladina akustického tlaku frekvenčne vázaného filtrem A (hladina akustického tlaku A), v jednotkách dB. Je to hodnota zvuku (hluku), kterou ukáže zvukoměr při použití váhového filtru A. Tento filtr potlačuje hodnoty v jednotlivých oktávových pásmech jak je uvedeno v následující tabulce.
Definice hladiny akustického tlaku A je dána vztahem
| LpA = 10 log ( 10( L1+K1)/10 + 10(L2+K2)/10 + …+ 10(Ln+K n)/10 ) |
(1.5) |
f (Hz) |
63 |
125 |
250 |
500 |
1000 |
2000 |
4000 |
8000 |
Ki |
-26.2 |
-16.1 |
-8.6 |
-3.2 |
0 |
1.2 |
1.0 |
-1.1 |
Příklad:
Hladina akustického tlaku A:
Frekvence (Hz): |
63 |
125 |
250 |
500 |
1000 |
2000 |
4000 |
8000 |
Hladiny zadané (dB): |
60.0 |
60.0 |
58.0 |
63.0 |
63.0 |
58.0 |
48.0 |
39.0 |
Hladiny korigované (dB): |
33.8 |
43.9 |
49.4 |
54.8 |
63.0 |
59.2 |
49.0 |
37.9 |
Výsledná hladina akustického tlaku A je 65.2 dB
Z hodnoty hladiny akustického tlaku A nelze ale zpětně určit hodnoty pro jednotlivé frekvence. Můžeme však určit maximální hodnoty, které nesmějí být překročeny, a to na základě podobnosti křivek N a hodnot hladin akustického tlaku A. Pro běžná spektra se doporučuje vztah
| LA = N + 5 | (1.6) |
Ekvivalentní hladina akustického tlaku je určena z časového rozložení hladin hluku LA podle vztahu
| LpAeg = 10 log(c1.10(L1 + K 1) / 10
+ c2.10( L 2 + K 2) /10 + ... + cn.10 ( L n + Kn) / 10 ) |
(1.7) |
Kde ci je relativní četnost hladiny Li.
HLADINA AKUSTICKÉHO TLAKU VE VOLNÉM PROSTORU
Ve volném prostoru (v poli přímých vln) platí pro výpočet akustického tlaku a akustického výkonu vztah
| Lp = LW + 10 log (Q / 4 pr2 ) | (1.8) |
kde LW je hladina ak. výkonu vyzařovaná rovnoměrně přes plochu koule 4pr2 a Q [-] je směrový činitel charakterizující umístění zdroje.
Pro zdroj vyjadřující do |
- celého prostoru je |
Q = 1 |
- poloprostoru (na zemi) |
Q = 2 |
|
- čtvrtiny prostoru (v hraně u stropu) |
Q = 4 |
|
- osminy prostoru (v rohu) |
Q = 8 |
Protože akustické hladiny výkonu i tlaku používají jednotku decibel je nutno neustále rozlišovat o jakou hodnotu se jedná. Na příkladu osvětlíme:
Pro přibližně bodový zdroj zvuku vyzařující rovnoměrně do všech směrů, tzn. že se akustická energie šíří ve tvaru kulových vlnoploch, platí
Lp = LW+ 10 log (Q / 4 pr2)
dosadíme-li za r = 1 metr a Q postupně 1, 2, 4 a 8 dostaneme
pro |
- volný prostor |
Lp = LW - 10 log 12.6 |
tj. |
Lp = LW – 11 |
|
- poloprostor |
Lp = LW - 10 log 6.3 |
tj. |
Lp = LW –8 |
/na zemi, stěně/ |
|
- čtvrtprostor |
Lp = LW - 10 log 3.1 |
tj. |
Lp = LW – 5 |
/v hraně u stropu/ |
|
- osminoprostor |
Lp = LW - 10 log 1.6 |
tj. |
Lp = LW – 2 |
/zdroj v rohu/ |
Příklad:
Pod oknem na podlaze stojí jednotka FC (Q=4), která pro nejnižší otáčky má udánu hladinu ak. výkonu LWA = 40 dB. Jaký bude hluk ve vzdálenosti 1 m a ve vzdálenosti 4 m.
- Hladina ak. tlaku v 1 m:
LpA = LWA + 10 log (4 / 4 p ) = 40 – 5 = 35 dB
- Hladina ak. tlaku ve 4 m:
LpA = LWA + 10 log (4 / 4 p 16 ) = 40 – 17 = 23 dB
ÚTLUM ZMĚNOU VZDÁLENOSTI
Z výše uvedeného vztahu lze odvodit pro praxi užitečný vztah
L2 – L1 = 20 log (r1 / r2)
například zdvojnásobením vzdálenosti klesne hladina akustického tlaku o 6 dB
Příklad:
Jaký bude hluk výše uvedené jednotky FC ve vzdálenosti 4 m, je-li hladina akustického tlaku A v 1 m od jednotky 35 dB:
L2 = L1 + 20 log (r1 / r2) = 35 + log (1/4) = 35 – 12 = 23 dB
HLADINA AKUSTICKÉHO TLAKU V UZAVŘENÉM PROSTORU
V uzavřeném prostoru (v poli odražených vln) pro výpočet ak. tlaku z ak. výkonu vztah
| Lp = LW + 10 log { ( 4 ( 1 - a )) / ( S . a ) } | (1.9) |
kde a
je střední hodnota činitele pohltivosti prostoru [ - ]
S je součet všech ploch v
místnosti
[ m2 ]
a |
bývá |
0,3 – 0,4 |
studia, divadla |
0,2 – 0,25 |
obchody, restaurace |
||
0,1 – 0,15 |
kanceláře, obytné místnosti |
||
0,05 |
tovární haly, plovárny, strojovny |
Výraz za logaritmem lze přibližně nahradit vztahem 4/A, často používaný v prospektech zahraničních výrobců, kde A [ m2 ] je tzv. celková absorpce prostoru.
Pak
| Lp = LW + 10 log ( 4 / A ) | (1.10) |
Příklad:
Jednotka má pro nejnižší otáčky udánu hladinu ak. výkonu LWA = 40 dB. Porovnejte ji s 2. jednotkou, má-li udánu hladinu ak. tlaku A 32 dB, stojí-li v prostoru s celkovou absorpcí A = 40 m2 (v kanceláři kde střední hodnota činitele pohltivosti prostoru a je 0.1 to představuje součet všech ploch S = 400 m2, neboť A z předcházejících vztahů je definováno přibližně pro malé a jako A = S . a ).
Hladina akustického výkonu 2. jednotky výpočtem bude:
LWA= Lp – 10 log ( 4 / 40 ) = 32 + 10 = 42 dB
Pro A = 200 by hladina akustického výkonu jednotky výpočtem byla:
LWA = Lp – 10 log ( 4 / 200 ) = 32 + 17 = 49 dB
Z toho vidíme, že výsledek závisí nejen na jednotce, ale značně i na velikosti a zvukové pohltivosti prostoru v kterém stojí.
Chceme-li porovnat akusticky dva prostory můžeme psát
| Lp1 = LW + 10 log (4/A1) | ||
| Lp2 = LW + 10 log (4/A2) | ||
| Lp1 – Lp2 = 10 log (A2/A1) | (1.11) |
Z toho plyne např., že vzroste-li celková absorpce prostoru A na dvojnásobek, klesne hladina ak. tlaku o 3 dB.
CELKOVÁ HLADINA AKUSTICKÉHO TLAKU V UZAVŘENÉM PROSTORU
Sčítá se účinek přímých vln a odražených:
| Lp = LW + 10 log ( Q / 4pr2 ) + 10 log { ( 4 ( 1 - a )) / ( S . a )} | (1.12) |
nebo zjednodušeně
| Lp = LW + 10 log ( Q / 4pr2 ) + 10 log ( 4 /A ) | (1.13) |