Využití stavových modelů v dynamických simulacích budov
Matematický opis lineárneho dynamického systému môžeme zostaviť definovaním fyzikálnych javov a zákonitostí alebo s využitím štatistickej analýzy experimentálne nameraných dát. U oboch metód hovoríme o identifikácii, pretože neznámy systém identifikujeme pomocou nám známych vzťahov. Článok sa zameriava na problematiku stavových modelov a ich uplatnenie pri riešení problémov vedenia tepla v budovách. Po vybudení reálnymi meteorologickými podmienkami tak bude možné simulovať dlhodobé priebehy tepelných záťaží miestnosti a v kombinácii s predpoveďou počasia predikovať vývoj vnútorných teplôt v krátkodobom časovom horizonte, čo umožní rozšíriť stratégiu riadenia o dlhodobé prerušované a útlmové režimy vykurovania.
1. Teoretický úvod
Priebeh posledných niekoľkých desaťročí je poznamenaný celospoločenským nárastom dopytu po energii vo všetkých jej formách. Napríklad, len na vykurovanie budov sa ročne spotrebujú asi dve tretiny ročnej produkcie tepla, čo pre veľké objekty ako sú školy, či administratívne budovy predstavuje enormné prevádzkové náklady. Z tohto dôvodu sa v súčasnosti hľadajú nové stratégie riadenia, ktoré by umožnili riadenie vykurovacích sústav takým spôsobom, aby sa požadovaných parametrov vnútorného prostredia budov dosiahlo v optimálnom čase a pri minimálnej spotrebe energie. To vo svojej podstate vedie na problematiku prediktívnych algoritmov, ktoré využívajú predpovede počasia a termodynamické modely. Tieto za získavajú na základe experimentálnych alebo analytických identifikačných postupov.
Predmetom identifikácie v teórii automatického riadenia je vyšetrenie dynamických parametrov objektu a zostavenie jeho matematického modelu. Tento sa najčastejšie získava vyhodnotením experimentálne nameraných údajov s využitím štatistickej analýzy. Metóda nevyžaduje vedomosti o štruktúre systému ani popis prebiehajúcich procesov, avšak môže byť extrémne náročná na čas a vybavenie. Rozhodujúci je správny výber výstupných dát, ktorých hodnoty musia byť fyzikálne závislé od vstupných parametrov. Vo všeobecnosti platí, že čím hlbšiu máme apriórnu informáciu o skúmanom objekte, tým lepší bude identifikačný experiment [1]. S použitím uvedeného postupu získame výpočtovo nenáročný opis systému, linearizovaný pre pracovné pole bodov. Nevýhodou je vysoká nestabilita metód a požiadaviek na predspracovanie meraných dát, rovnako ako ťažko fyzikálne zdôvodniteľné koeficienty stavového opisu [2].
Analytické identifikačné postupy naproti tomu vyžadujú znalosť fyzikálno-chemických pochodov prebiehajúcich v skúmanom objekte a ich matematického opisu. K riešeniu môžeme pristupovať dvoma rozličnými spôsobmi, a to pomocou modelov so sústredenými parametrami, kedy vzťahy medzi vstupmi a výstupmi majú tvar obyčajných diferenciálnych rovníc s deriváciou podľa jednej premennej alebo s rozloženými parametrami, ak vytvorené parciálne diferenciálne rovnice majú derivácie podľa času a priestorových premenných.
1.1 Rovnica neustáleného vedenia tepla
Problematikou neustáleného vedenia tepla v telesách sa už začiatkom 19. storočia zaoberal francúzsky matematik a fyzik Jean Baptiste de Fourier. Ten v roku 1807 sformuloval zákon vedenia tepla [3]
ktorý popisuje lineárnu závislosť medzi hustotou tepelného toku ![]() [W/m2] a gradientom teploty v smere definovanej súradnej sústavy, ktorých konštantou úmernosti je súčiniteľ tepelnej vodivosti materiálu λ [W/m‧K].
[W/m2] a gradientom teploty v smere definovanej súradnej sústavy, ktorých konštantou úmernosti je súčiniteľ tepelnej vodivosti materiálu λ [W/m‧K].
Neskôr, v roku 1822 predstavil rovnicu kontinuity nestacionárneho tepelného toku, ktorá popisuje tepelnú bilanciu elementárneho objemu hmoty. Ak navyše uvažujeme hrúbku telesa nekonečne malú v porovnaní s jeho ďalšími rozmermi, môže sa rovnica zjednodušiť na tvar
kde T (K) je teplota telesa, ρ (kg/m3) hustota, c (J/kg∙K) špecifická tepelná kapacita a λ (W/m∙K) predstavuje tepelnú vodivosť. Uvedené materiálové charakteristiky sú vo všeobecnosti funkciou teploty a relatívnej vlhkosti, ale pre potreby výpočtov v technike prostredia sú obvykle nahrádzané priemernými hodnotami. Diferenciálnu rovnicu vedenia tepla možno zaradiť do skupiny parciálnych diferenciálnych rovníc, ktoré možno riešiť analyticky po zavedení určitých zjednodušení. Medzi tieto patria napríklad predpoklady homogenity a invariantnosti okolitého prostredia. Riešením sa potom rozumie nájdenie teploty ako funkcie polohy a času v závislosti na geometrickom tvare telesa, jeho fyzikálnych vlastnostiach a počiatočných, či okrajových podmienkach [4].
Medzi najčastejšie používané metódy patrí transformácia do frekvenčnej oblasti, čím sa eliminuje čas ako nezávislá premenná a výsledné algebrické riešenie dostávame za rovnakých okrajových podmienok. Vzhľadom k závažným problémom s numerickým hľadaním koreňov charakteristickej rovnice je metóda nahrádzaná efektívnejšími postupmi, ako bude ďalej nasledovať.
Početné práce venované tejto problematike naznačujú, že simulačné modely využívajúce analytické riešenie sú v prípade lineárnych systémov dokonca efektívnejšie, než metóda konečných diferencií a to z dôvodu, že časový interval je tu zvolený len s ohľadom, ako presne reprezentuje náhradná krivka skutočný priebeh teploty.
1.2 Metóda stavového priestoru
Matematický aparát, založený na pojmoch vnútorného stavu a vnútorného popisu, bol vytvorený začiatkom 60-tych rokov minulého storočia. Na rozdiel od klasických modelov vychádza metóda z poznatku, že priebeh procesu v dynamickom systéme závisí nielen od veľkosti vybudenia, ale aj jeho predchádzajúceho vývoja, charakterizovaného okamžitým vnútorným stavom [5].
Seem [6] analogicky s metódou konečných diferencií ukázal, že vhodnou diskretizáciou priestoru možno parciálnu diferenciálnu rovnicu vedenia tepla zredukovať na lineárny systém, kde vzťahy medzi vektorovými veličinami môžu byť vyjadrené sústavou diferenciálnych rovníc s konštantnými koeficientmi a systémom algebrických rovníc, reprezentovaných rovnicou stavu systému a rovnicou výstupu nasledovne
kde je
- A
- – matica vnútorných väzieb systému
- B
- – matica vstupných premenných
- C
- – matica výstupných premenných
- D
- – matica priamej väzby vstupu na výstup
- x(t)
- – vektor stavových premenných
- u(t)
- – vektor vstupných premenných
- y(t)
- – vektor výstupných premenných
Pre systémy, ktorých výstupné vektory závisia len od stavových premenných potom rovnica výstupu neobsahuje žiadne vstupné veličiny, teda matica priamej väzby vstupného signálu na výstup bude nulová.
2. Model dynamickej odozvy miestnosti
Vychádzajúc z poznatkov nadobudnutých predchádzajúcou teoretickou analýzou, aplikujme teraz vyššie uvedený postup na problematiku prenosu tepla v budovách. Metóda stavového priestoru sa oproti klasickým postupom vyznačuje pomerne vysokou presnosťou a tým, že termodynamický model je reprezentovaný sústavou matíc, a teda môže byť pomerne jednoducho implementovaný v prediktívnom type regulátora. Navyše, v prípade, že okrajové podmienky modelu budú zadané formou linearizovaných meteorologických dát, môžeme sledovať priebehy tepelných záťaží budov a s využitím predpovedí počasia tak predikovať vývoj vnútorných teplôt v krátkodobom časovom horizonte.
Za účelom vyšetrenia dynamických vlastností riadeného objektu teraz uvažujme modelovú učebňu v tvare kvádra s rozmermi 8 x 5 x 3,5 metra, umiestnenú na druhom nadzemnom podlaží školskej budovy. Obvodová stena s presklením na severozápad je uvažovaná monolitická, z betónového bloku o konštantných tepelnoizolačných parametroch. Vnútorné priečky sú tvárnicové, podlahy a stropné konštrukcie tvoria železobetónové dosky bez prídavnej izolácie.
2.1 Energetická bilancia a kapacitný model
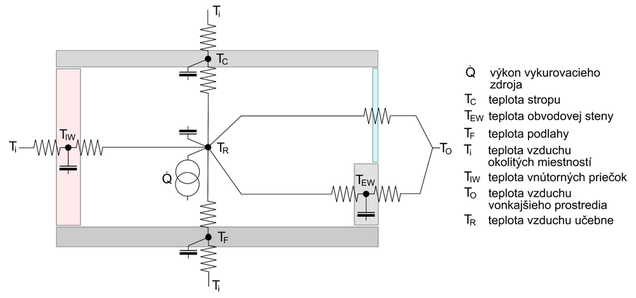
Modelový objekt je pre potreby simulácie nahradený zjednodušeným kapacitným modelom, ktorý nezahŕňa straty vetraním, infiltráciu ani radiačné zisky (obr.1). Vykurovanie v miestnosti sa uvažuje čisto konvektívne so zanedbateľnou radiačnou zložkou, teda všetok vykurovací výkon sa odovzdá vzduchu v miestnosti.
Ak predpokladáme konštantné rozloženie teplôt v priereze, môžeme tepelnoakumulačné parametre každej zo stien modelovej miestnosti sústrediť do jednoduchého elektrického obvodu, tvoreného odporom a kondenzátorom. Výsledný kapacitný model bude potom vytvorený z konečného počtu modelov prvého rádu v sério-paralelnom zapojení, kde jednotlivé uzly vyjadrujú pohyb tepelných stavov systému v n-rozmerovom priestore. Pre každý z uzlov náhradného modelu potom možno zostaviť energetickú bilanciu, čoho výsledkom je sústava obyčajných diferenciálnych rovníc v tomto tvare
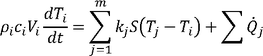 (5)
(5)
kde V [m3] je objem elementu, S [m2] plošný rozmer steny a k [W/m2‧K] súčiniteľ prechodu tepla konštrukciou. Prevedením sústavy takto zostavených bilančných rovníc do maticového tvaru potom dostávame matice stavového opisu, spoločne s ich príslušnými koeficientmi. V prípade zložitých modelov je tieto nutné zjednodušiť, čo sa v praxi najčastejšie robí pomocou matematickej redukcie alebo transformáciou na prenosovú maticu vhodného rádu.
2.2 Simulácia priebehu vnútornej teploty
Pre analýzu dynamických systémov existuje v súčasnosti celá rada komerčných programových balíkov. Tieto sa prevažne zameriavajú na energetické simulácie, ale vo všeobecnosti neumožňujú priame prepojenie modelu s regulátorom. Z pohľadu simulácií vnútorného prostredia budov a ich riadiacich systémov patrí medzi najvýznamnejšie programovacie jazyky Matlab/Simulink, založený na maticovom počte a umožňujúci riešiť širokú oblasť numerických problémov.
Dosadením dynamických rovníc (3) a (4) systému do bloku [state-space] dostávame definovaním počiatočných a okrajových podmienok, nasledovné odozvy vnútornej teploty v miestnosti.
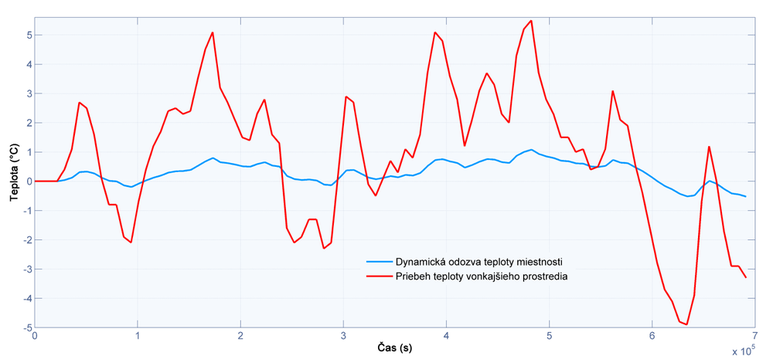
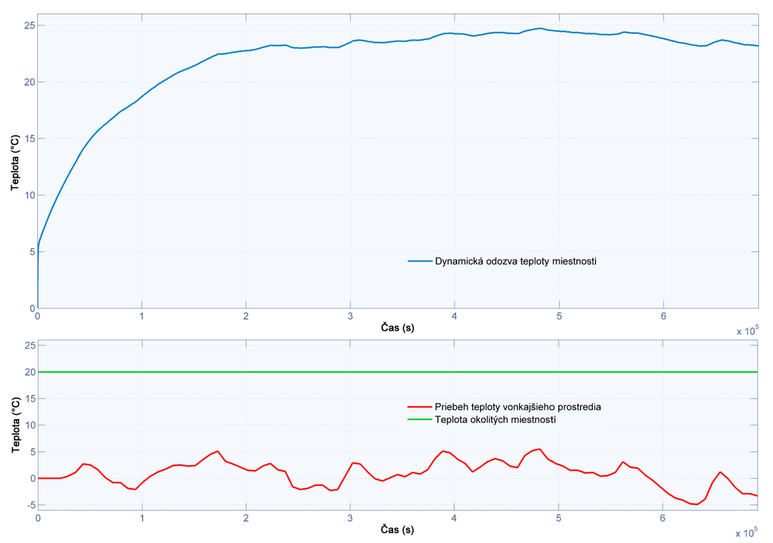
V prípade vybudenia modelu premenlivými parametrami vonkajšieho prostredia, bude dynamická odozva teploty miestnosti (obr.2) kopírovať definovaný priebeh s určitým teplotným oneskorením a útlmom, ktorých intenzita závisí len od tepelnoakumulačných parametrov konštrukcie. Ak navyše uvažujeme časovo-stále teploty okolitých miestností bude mať, po zapnutí vykurovacieho zdroja s konštantným výkonom, priebeh vnútornej teploty exponenciálny charakter (obr.3).
3. Záver
Uvedený postup sa využíva pri vytváraní tepelných modelov a simuláciách dynamického správania vnútorného prostredia budov. Po spresnení modelu a jeho verifikácii na reálnom objekte tak bude možné predikovať vývoj vnútorných teplôt experimentálnej miestnosti a zároveň tak efektívne riadiť reguláciu vykurovacej sústavy, najmä z pohľadu prerušovaných režimov vykurovania.
4. Poďakovanie
Článok bol spracovaný s finančnou podporou grantového projektu GAČR 101/09/H050 „Výzkum energeticky úsporných zařízení pro dosažení pohody vnitřního prostředí“ a projektu FSI-S-11-6 s názvom „Komplexní modelování interakce člověka a prostředí v kabinách dopravních prostředků a obytných prostorách a návrhové nástroje“.
5. Literatúra
- [1] MEJRI, O; PALOMO DEL BARRIO, E; GHRAB-MORCOS, N. Energy performance assessment of occupied building using model identification techniques. Energy and Buildings. 2011, s. 285–299.
- [2] LJUNG, L. System identification: theory for the user. 2nd edition. Upper Saddle River: Pretince Hall, 1999, 609 s. ISBN 01-365-6695-2.
- [3] DUŠKA, M. Akumulace tepla ve výpočtu tepelné zátěže klimatizovaných prostorů. Praha, 2010. xi, 161 s. Dizertačná práca. České vysoké učení v Praze.
- [4] ŘEHÁNEK, Jaroslav. Tepelná akumulace budov. Praha: ČKAIT, 2002. 276 s. ISBN 80-86364-59-3.
- [5] ŠVARC, I. Teorie automatického řízení 1. Druhé vydání. Brno: Vysoké učení technické, 1992, 210 s. ISBN 80-214-0516-3.
- [6] SEEM, J. E. Modelling of heat transfer in buildings. Madison, 1987, 171 s. Dizertačná práca. Dept. of Mechanical Engineering. University of Wisconsin-Madison.
Autorka vo svojom článku prezentuje problematiku simulácií tepelných záťaží budov osobitne potom nových modelov zohľadňujúcich vplyv reálnych meteorologických zaťaží a ich súvis s presnou predikciou vnútorných teplôt v budovách. Kvalitné prediktívne modely sa v tejto oblasti ukazujú ako vhodný nástroj pri tepelnej regulácii najmä (ale nie len) v režime prerušovaného vykurovania ako i pri útlmových alebo nábehových režimoch. Autorkou prezentovaný Model dynamickej odozvy miestnosti ako i jeho zjednodušenie pomocou kapacitného modelu so zaújmavými elektrickými analógiami je nepochybne podnetným príspevkom v tejto oblasti a podľa môjho názoru stojí za uverejnenie v odbornej tlači.
Je zrejmé, že príspevok sa do istej miery týka hraničnej oblasti tepelného inžinierstva a aplikovanej teórie regulácie a automatizácie a ako taký osloví menšinu čitateľov TZB. Napriek tomu môžem konštatovať, že príspevok je vecne a formálne správny, je zaújmavý a týka sa problematiky, ktorou sa časopis TZB zaoberá. Doporučujem teda jeho publikáciu.
Mathematical description of a linear dynamic system can be obtained in various ways. Theoretical models are desirable when basic physical laws of nature are known that describes the relationship between input and output signals, mostly in terms of differential equations. If this is not case, approximate dynamic characterization may be received from the statistical analysis of experimental data. The paper describes techniques used in building thermal simulations, with particular focus on state-space models. If excited by real meteorological conditions, momentaneous temperature variations in an enclosure could be computed that are prerequisites for analysis of long-term heating loads, particularly if the model is exploited as a part of the advanced control system.