Posuzování tepelně izolačních vlastností teplovodního potrubí I.
Část 1 – Prostup tepla stěnou potrubí
Článek uvádí základní vztahy pro určení tepelné ztráty u teplovodního potrubí s tepelnou izolací z rozdílů teplot vnitřního a venkovního prostředí u rovinného a válcového tvaru. Výpočet vychází ze součinitele prostupu tepla podle součinitele vodivosti a součinitelů přestupu tepla.
Voda proudící potrubím s teplotami (θi) je ochlazována na stěnách potrubí v závislosti na tepelném odporu stěny potrubí, tepelném odporu izolace a na teplotě v okolí potrubí (θu). Prostup tepla stěnou potrubí je sestaven z přestupů tepla, popsaných součiniteli přestupu na straně vnitřní (hi) a na straně vnější (hu).
Přestup tepla závisí především na rychlosti proudící vody potrubím a rychlosti proudění vzduchu podle povrchů stěny potrubí, případně na drsnosti povrchu a turbulenci. Vedení tepla stěnou potrubí a vedení v izolační vrstvě je přesnější částí výpočtu prostupu tepla stěnou, pokud správně volíme součinitele vodivosti materiálů (λ).
Množství tepla (QZ), které prochází stěnou potrubí a izolační vrstvou o teplotě vody (θi) do vnějšího vzduchu s teplotou (θu) v okolí potrubí, je možné zjednodušeně stanovit ze vztahu:
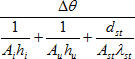(1)
[W]
kde je
- Δθ
- rozdíl mezi teplotou vody a teplotou vzduchu v okolí potrubí (θi − θu) [°C]
- Ai
- vnitřní plocha potrubí [m2]
- Au
- vnější plocha povrhu stěny potrubí (izolace) [m2]
- Ast
- plocha v ose stěny potrubí, v níž probíhá vedení tepla [m2]
- hi
- součinitel přestupu tepla na vnitřní straně [W/m2.K]
- hu
- součinitel přestupu tepla na vnější straně [W/m2.K]
- λst
- součinitel vodivosti materiálu stěny [W/m.K]
- dst
- tloušťka stěny potrubí [m].
Prostup tepla rovinnou stěnou si můžeme demonstrovat na hranatém potrubí nebo na tenké stěně potrubí velkého průměru. Na obr. 1 je zobrazen průběh teploty stěnou potrubí při rovinném prostupu tepla. Na obr. 1 je výpočtová teplota vody označena symbolem (θi) a teplota vzduchu v okolí hranatého potrubí je (θu). Tloušťka stěny jednovrstvého potrubí je označena symbolem (d).
Prostup tepla rovinnou stěnou
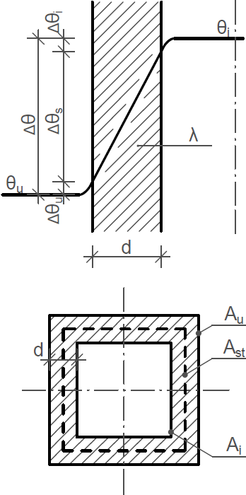
Obr. 1 Výpočtové schéma prostupu tepla potrubím – rovinnou stěnou
θ – teplota, Δθ – teplotní spád, λ – součinitel vodivosti materiálu, d – tloušťka stěny (vrstvy), Ai – vnitřní plocha povrchu stěny, Au – vnější plocha povrchu stěny, Ast – střední plocha vrstvy stěny
U neizolovaného potrubí většího průměru, ale zejména při malé tloušťce stěny potrubí je přírůstek vnější plochy potrubí oproti vnitřní ploše potrubí zanedbatelný. Proto volíme často konstantně A = Ai = Au = Ast a vztah (1) je pak zjednodušen na:
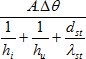(2)
[W]
Podle vztahu (2) vychází součinitel prostupu tepla rovinnou jednovrstvou stěnou:
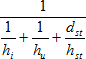(3)
[W/m2.K]
Průběh teplot u jednovrstvé rovinné stěny je lineární.
Prostup tepla válcovou stěnou
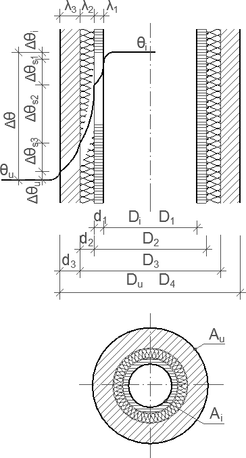
Obr. 2 Výpočtové schéma prostupu tepla potrubím – vícevrstvou válcovou stěnou
θ – teplota, Δθ – teplotní spád, λ – součinitel vodivosti materiálu, d – tloušťka stěny (vrstvy), D – vnitřní průměr stěny (vrstvy), A – plocha povrchu stěny (vrstvy)
Indexy: řada 1, 2, 3 ... pořadí od osy; i – vnitřní, u – vnější (okolí), s – stěny
Pro výpočtové schéma je zvoleno potrubí kruhového průřezu a zároveň je potrubí tepelně izolované. Prostup tepla je tedy vícevrstvou stěnou. Prostup tepla může být vztažen k vnější nebo vnitřní válcové ploše (Ai) nebo k vnější ploše izolační vrstvy (Au).
Pro prostup tepla válcovou stěnou můžeme použít tedy vztah:
Pro výpočet prostupu je pak nutné stanovit buď součinitel prostupu tepla vztažený na vnitřní plochu potrubí, označovaný nejčastěji (Ui), nebo součinitel prostupu tepla vztažený na vnější válcovou plochu, označený (Uu).
Pro zjednodušení si uveďme pouze vztah pro výpočet součinitele prostupu tepla vícevrstvé stěny potrubí, vztažený na vnitřní plochu potrubí s průměrem (Di) a pak lze stanovit:
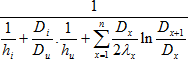(5)
[W/m2.K]
kde je
- Di, Dx, Du
- vnitřní průměr potrubí, resp. průměr x-té vrstvy stěny (D1, D2, D3…), resp. průměr vnějšího povrchu izolace [m]
- λx
- součinitel vodivosti materiálu x-té vrstvy potrubí a izolace [W/m.K]
Průběh teplot válcovou vícevrstvou stěnou je nelineární, neboť průběh teplot je ovlivněn zvětšováním plochy směrem prostupu tepla.
Výpočtová doporučení pro stanovení prostupu tepla
Součinitel prostupu tepla
Klasický výpočet prostupu tepla stěnou potrubí bývá doplňován, zpřesňován nebo zjednodušován, a to velmi často pro parametry konkrétního složení tepelné izolace a pro parametry okolního prostředí. Často jsou podkladem pro tepelné ztráty v potrubí i klasické topenářské podklady, vycházející ze stanovení výkonu otopného tělesa z hladkých trubek.
V literatuře se často uvádí zjednodušený vztah prostupu tepla:
- pro tepelně izolované kovové trubky
U =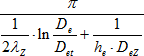
[W/m2K]
- pro tepelně neizolované kovové trubky
U =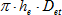
[W/m2K]
kde je
- λZ
- součinitel tepelné vodivosti tepelné izolace [W/mK]
- he
- součinitel přestupu tepla na vnějším povrchu [W/m2K]
- DeZ
- vnější průměr vrstvy tepelné izolace [m]
- Det
- vnější průměr trubky [m]
Součinitel přestupu tepla
Někdy se uvádí součinitel přestupu tepla na vnějším povrchu (he) v závislosti na povrchové teplotě tepelné izolace a na teplotě okolí.
Pro stanovení součinitele přestupu tepla (he) z teplotního rozdílu povrchové teploty a teploty okolí se uvádí někdy též vztah:
kde je
- θpe
- povrchová teplota tepelně izolačního obalu trubky [°C]
- θu
- teplota okolí [°C]
Podle ČSN EN ISO 12 241 se uvádí empirické vztahy výpočtu součinitele přestupu tepla na vnějším povrchu tepelné izolace při samostatném vedení potrubí ve vodorovné nebo svislé poloze.
Pro vodorovné potrubí uvnitř budovy je vnější součinitel přestupu tepla:
- při laminární konvekci s platností v intervalu De3 (θpe − θu) ≤ 10
he = 1,25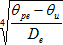
[W/m2K]
- při turbulentní konvekci s platností v intervalu De3 (θpe − θu) > 10
he = 1,21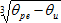
[W/m2K]
Pro svislé potrubí uvnitř budovy s výškou trubky H je vnější součinitel přestupu tepla:
- při laminární konvekci s platností v intervalu H3 (θpe − θu) ≤ 10
he = 1,32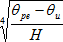
[W/m2K]
- při turbulentní konvekci s platností v intervalu H3 (θpe − θu) > 10
he = 1,74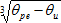
[W/m2K]
Posuzování tepelně izolačních vlastností teplovodního potrubí.
- Část 1 – Prostup tepla stěnou potrubí
- Část 2 – Teoretické zásady ochlazování vody při průtoku
- Část 3 – Příklad výpočtu exponenciálního průběhu ochlazování
- Část 4 – Navrhování tepelné izolace podle ČSN EN 12 828
- Část 5 – Příklady ochlazování potrubí u teplovodního vytápění
Předložený soubor článků řeší aplikaci teorie sdílení tepla na problematiku ochlazovaní teplovodního potrubí.
V první části je shrnuta obecná teorie prostupu tepla stěnou potrubí aplikovaná na rovinnou stěnu a potrubí kruhového průřezu. Závěr první části je zaměřen na stanovení součinitele prostupu tepla potrubí.
Druhá část článku řeší problematiku ochlazování potrubí v tepelné síti a aplikace teoretických postupů na ochlazování cirkulačního potrubí teplé vody.
Třetí část na příkladu exponenciálního průběhu ochlazování za různých extrémních okrajových podmínek demonstruje účinek tepelné izolace potrubí a v závěrech jsou shrnuty hlavní faktory ovlivňující ochlazování potrubí s teplonosnou látkou.
Ve čtvrté části pak autor řeší otázky spojené s normovým návrhem tepelné izolace potrubí tepelných soustav v budovách a v přehledných tabulkách uvádí základní parametry a hodnoty potřebné pro výpočet.
V závěrečné, páté části článku jsou aplikovány teoretické principy na teplovodní otopnou soustavu a je zdůrazněn vazba mezi tepelnou ztrátou potrubní sítě a rychlostí proudění teplonosné látky.
Soubor článků představuje ucelený pohled na teorii i praxi problematiky izolace potrubí s podrobným teoretickým základem i příklady aplikace. Doporučuji k publikaci.Article features basic relations for determination of heat loss at warmwatter tube with thermal isolation from differences of flue watter temperature and ambient air temperature at planar and cylindric form. Calculation coming-out from coefficient of heat transmission according to coefficient of thermal conductivity and coefficents of heat transfer.