Postup a výsledky kontroly optických prevažovacích prístrojov
Vytyčovanie a kontrola zvislého smeru patrí medzi často riešené úlohy i v stavebníctve. K prístrojom, ktoré sa používajú pri vytyčovaní zvislíc patria optické prevažovacie prístroje (optické premietače). Najčastejšie používaným prístrojom je prístroj Zeiss PZL (Zeiss Zenitholt PZL 100). Príspevok popisuje postup a výsledky testovania podľa STN ISO 17123-7: 2010 Optika a optické prístroje – Postupy na testovanie geodetických prístrojov. 7. časť: Optické prevažovacie prístroje.
1. Úvod
K prístrojom ktoré sa používajú pri kontrole zvislosti a vytyčovaní zvislíc v stavebníctve patria aj optické prevažovacie prístroje (optické premietače). Optický prevažovač, používaný v stavebníctve i v geodézii je prístroj zo zvislou zámernou priamkou, ktorej zvislú polohu zabezpečuje urovnaná libela alebo kompenzátor. Často používaným prístrojom na túto činnosť je prístroj Zeiss PZL (Zeiss Zenitholt PZL 100). Podobne ako pri iných geodetických prístrojoch a pomôckach je jeho kontrola a testovanie dôležitou súčasťou využívania v praxi. Kontrolu optických prevažovacích prístrojov umožňuje aj norma z oblasti pôsobnosti medzinárodnej technickej komisie ISO/TC 172/SC 6 – Optics and optical instruments /Geodetic and surveying instruments (Optika a optické prístroje/Geodetické a meracie prístroje): STN ISO 17123-7: 2010 Optika a optické prístroje – Postupy na testovanie geodetických prístrojov. 7. časť: Optické prevažovacie prístroje [1].
2. Postupy na testovanie geodetických prístrojov – optické prevažovacie prístroje
STN ISO 17123-7 špecifikuje skúšobné postupy, zamerané na určovanie a odhad presnosti optických prevažovacích prístrojov používaných pri meraniach v stavebníctve a geodézií. Cieľom týchto skúšok je najmä overenie vhodnosti jednotlivých prístrojov pre príslušnú úlohu a splnenie požiadaviek iných noriem. Postupy sú určené na skúšanie prístrojov v teréne bez potreby ďalších zariadení a sú navrhnuté tak, aby bol minimalizovaný vplyv atmosférických podmienok na výsledok testu [1, 4].
2.1. Základná charakteristika a princíp merania optickým prevažovačom Zeiss PZL 100
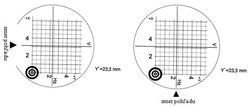
Optický prevažovač Zeiss PZL 100 (obr. 1) je prístroj, ktorého zámerná os je zvislá a zvislicu je možné vytýčiť len smerom do zenitu. Zámerný kríž optického prevažovača pozostáva z dvojice dvoch na seba kolmých rysiek – vodorovnej a zvislej (obr. 2). Vodorovná ryska je urovnávaná kompenzátorom a zvisla pomocou alidádovej libely. Nižšia presnosť urovnania zvislej rysky spôsobuje, že pri presných prácach sa na vytyčovanie používa iba vodorovná ryska.
Aby sa odstránila chyba z urovnania vodorovnej rysky vplyvom chyby kompenzátora, vytýčenie sa vykonáva v dvoch navzájom o 180° pootočených polohách. Polohu bodu na cieľovej značke (terči), ktorým prechádza zvislica realizovaná optickým prevažovačom, sa určuje v štyroch polohách, vzájomne pootočených o 90°. Cieľová značka je tvorená milimetrovým rastrom s vyznačením orientácie jednotlivých osí (obr. 2). Horizontáciu prevažovača zaistíme pomocou urovnávacích skrutiek a alidádovej libely, upevnenej na prístroji (alidáde), v dvoch na seba kolmých smeroch [3].
Spriemerovaním hodnôt súradníc z prvej a druhej polohy získavame výslednú polohu bodu (y, x) na cieľovej značke:
Optický prevažovač dosahuje presnosť vytýčenia zvislice vyjadrenú pomernou presnosťou 1 až 2 : 100 000. Presnosť vytýčenia zvislice je priamoúmerne hodnote prevýšenia medzi prevažovačom a cieľovou značkou (pri prevýšení h = 100 m je presnosť vytýčenia 1 až 2 mm). Presnosť takto vytýčenej zvislice môžeme vyjadriť strednou chybou vytýčenia zvislice v smere osi y alebo x, ktorú vypočítame podľa vzťahu [2]:
kde h je prevýšenie medzi optickým prevažovačom a cieľovou značkou, vyjadrené v milimetroch.
Stredná polohová chyba vytýčenia bodu, ktorým prechádza zvislica, je potom daná vzťahom
Ak uvažujeme aj presnosť centrácie prístroja nad bodom, v tom prípade bude potrebné k celkovej strednej polohovej chybe vytýčenia bodu zahrnúť aj túto hodnotu [2, 3].
2.2 Testovanie prístroja PZL podľa STN ISO 17123-7: 2010 Optika a optické prístroje – Postupy na testovanie geodetických prístrojov. 7. časť: Optické prevažovacie prístroje
Norma definuje skúšobné postupy, ktoré sa používajú pri určovaní a stanovení presnosti počas používania optických prevažovacích prístrojov pre meračské účely. Postupy uvedené v tejto norme sa týkajú používania prístrojov v stavebnej praxi pre kontrolné a overovacie merania a zároveň umožňujú určenie presnosti meraných údajov [4].
Presnejšie výsledky sú získané pri laboratórnych podmienkach, ale dôveryhodnejšie výsledky budú dosiahnuté, ak sa prostredie prispôsobí podmienkam, v akých bude realizovaná plánovaná úloha. Ako cieľová značka používa terč na, ktorom je pripevnená pravouhlá mriežka x – y, kde veľkosť intervalu mriežky t musí spĺňať:
kde h je prevýšenie medzi optickým prevažovačom a cieľovou značkou, vyjadrené v metroch (prevažovaná výška), Γ je zväčšenie ďalekohľadu (u Zeiss PZL 100 je zväčšenie 31,5násobné), 2,9 je konštantný faktor umožňujúci dobrý odhad veľkosti mriežky [4].
Presnosť určenia polohy bodu pri optických prevažovacích prístrojoch je priamoúmerne závislá na hodnote prevýšenia medzi prevažovačom a cieľovou značkou. Relatívna empirická stredná chyba sISO– plumb vyjadruje presnosť, ktorá sa dosiahne pri určení jedného bodu s príslušným prevažovaným prevýšením. Skúšobné postupy umožňujú tri nasledujúce kombinácie:
- jeden merač, jeden prístroj počas celého prebiehajúceho merania,
- jeden testovaný prístroj za rôznych atmosférických podmienok,
- dva prístroje testované za rovnakých atmosférických podmienok [4].
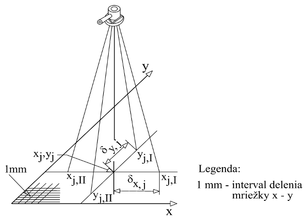
Konfigurácia pri testovaní pozostáva s optického prevažovača, cieľovej značky reprezentovanej mriežkou x – y s intervalom delenia, ktorý má spĺňať podmienku uvedenú vo vzťahu (4). Cieľová značka má byť umiestnená vo výške približne rovnakej ako je výška pri plánovanej meračskej úlohe. Pred začatím merania je potrebné prístroj aklimatizovať. Teplotnému rozdielu 1 °C sa odporúča dĺžka aklimatizácie cca 2 minúty. Pri testovaní sa vykonávajú sa tri série meraní (m = 3), kde každá séria sa skladá s 10 opakovaní (n = 10). Medzi jednotlivými sériami meraní sa poruší horizontácia a prístroj sa opakovane horizontuje. Výsledkom merania sú dva súbory meraných údajov jeden pre hodnoty na x-ovej osi (xj,I, xj,II) a druhý pre hodnoty na y-ovej osi (yj,I, yj,II) [4].
2.3 Testovanie vybraných prístrojov Zeiss PZL 100
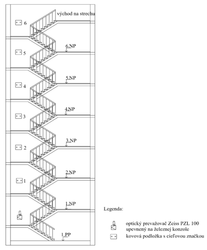
Optický prevažovač sa využíva v geodetickej praxi vo väčšine prípadov na vytýčenie zvislice v smere nahor. Vytýčením zvislice sa kontrolujú zvislosť a náklony stavebných objektov, z ktorých je možné odvodiť vodorovné posuny pozorovaných bodov a objektov. Pri realizácii takýchto meraní sa nepoužije jeden pozorovaný bod, ale množina vhodne rozmiestnených pozorovaných bodov na danom objekte. Preto aj pri testovaní optického prevažovača Zeiss PZL 100 bola zvolená za pozorovaný objekt 7poschodová budova s výškou 25 m. Rez stavebným objektom s vyznačením polohy pozorovaných bodov a prístroja je na obr. 3.
Pri testovaní bola zvolená metóda s dvoma prístrojmi (prístroj č. 1 a č. 2), za rovnakých atmosférických podmienok. Umiestnenie prístrojov bolo počas celého testovania nemenné, obr. 4. Pozorované body boli umiestnené na medziposchodiach vo výške približne 1,80 m od podesty a stabilizované pomocou kovovej podložky, ktorá bola pevne spojená so stenou. Podložka zabezpečovala trvalú stabilizáciu bodu (obr. 4a). Pozorované body boli signalizované dočasne, a to pomocou cieľovej značky, na ktorej je upevnená mriežka x – y s intervalom delenia 1 mm (obr. 4b). V tabuľke 1 je uvedený zoznam pozorovaných bodov s prevažovanými výškami h [3].
| Pozorovaný bod | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Prevažovaná výška h [m] | 4.450 | 8.520 | 12.330 | 16.260 | 20.180 | 23.740 |
2.4 Spracovanie nameraných údajov
Na každom so šiestich bodov boli vykonané tri série meraní (m = 3), kde každá séria sa skladá s 10 opakovaní (n = 10), pre oba prístroje [4].
Meranie každej série je hodnotené samostatne, rozdiely medzi xj,I a xj,II respektíve yj,I a yj,II sú hodnoty odchýlok xj ![]() yj (obr. 5), [4]:
yj (obr. 5), [4]:
kde j = 1, ..., 10.
Ďalším krokom je výpočet kvázi – odčítaní xj a yj podľa vzťahu (6):
kde j = 1, ..., 10, xj je stredná hodnota z meraní xj,I a xj,II , yj je stredná hodnota z meraní yj,I a yj,II. Priemerné hodnoty kvázi – odčítaní sú vypočítané podľa vzťahu (7) a stredné hodnoty odchýlok podľa (8)
Z priemerných hodnôt kvázi – hodnôt sa vypočítajú opravy rx,j a ry,j:
Výsledné súčty opráv v jednotlivých osiach x a y budú mať tvar:
kde ![]() je súčet štvorcov rezíduí v smere osi x,
je súčet štvorcov rezíduí v smere osi x, ![]() je súčet rezíduí v smere osi y. Celkový súčet štvorcov rezíduí
je súčet rezíduí v smere osi y. Celkový súčet štvorcov rezíduí ![]() bude mať tvar:
bude mať tvar:
Výpočet empirických štandardných odchýlok prenášaného bodu pre jednotlivé zložky x a y pre danú prevažovanú výšku:
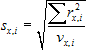 a
a 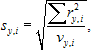 (12)
(12)
kde vx,i = vy,i = 10 − 1 = 9 je počet stupňov voľnosti v x-ovej a y-ovej zložke. Empirickú štandardnú odchýlku prenášaného bodu získame zo vzťahu
kde vi = 20 − 2 = 18 je počet stupňov voľnosti (počet nadbytočných meraní) pre obe polohy. Vzhľadom na obmedzený rozsah príspevku sú uvedené jednotlivé hodnoty empirických stredných odchýlok (i ostatné výsledky testovania) len pre prístroj č. 1 – tab. 2 [3].
| Prístroj č. 1: Zeiss PZL 100, v.č. 214 456 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Č. bodu | 1 | 2 | 3 | 4 | 5 | 6 | ||
| s [mm] | ||||||||
| 1. meranie | Séria | 1 | 0.06 | 0.08 | 0.13 | 0.15 | 0.61 | 0.54 |
| 2 | 0.05 | 0.08 | 0.11 | 0.14 | 0.81 | 0.57 | ||
| 3 | 0.05 | 0.06 | 0.09 | 0.11 | 0.67 | 0.63 | ||
| 2. meranie | Séria | 1 | 0.07 | 0.12 | 0.13 | 0.25 | 0.69 | 0.73 |
| 2 | 0.07 | 0.14 | 0.13 | 0.27 | 0.84 | 0.79 | ||
| 3 | 0.07 | 0.13 | 0.10 | 0.21 | 0.74 | 0.74 | ||
Kompletný počet stupňov voľnosti pre všetky série meraní sa vypočíta
Výsledná empirická štandardná odchýlka prenášaného bodu v oboch polohách prístroja má tvar, (vypočítaná zo všetkých troch sérií meraní):
Pomernú presnosť vyjadríme v tvare:
s je hodnota vypočítaná zo vzťahu (15), h je prevažovaná výška [4].
Odhadovaná odchýlka od zvislice sa môže vyjadriť v smere osi x a y samostatne zo všetkých sérii meraní a výsledná hodnota odchýlky je vyjadrená vzťahom (18):
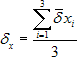 a
a 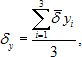 (17)
(17)
Empirická stredná chyba odchýlky δ
| Prístroj č. 1: Zeiss PZL 100, v.č. 214 456 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Č. bodu | 1. meranie | 2. meranie | ||||||||||
| s [mm] | s ISO– plumb | δx [mm] | δy [mm] | δ [mm] | sδ [mm] | s [mm] | s ISO– plumb | δx [mm] | δy [mm] | δ [mm] | sδ [mm] | |
| 1 | 0.05 | 1:82900 | −0.03 | −0.03 | 0.05 | 0.010 | 0.07 | 1:61100 | −0.03 | −0.02 | 0.04 | 0.013 |
| 2 | 0.08 | 1:112800 | −0.06 | −0.06 | 0.09 | 0.014 | 0.13 | 1:64900 | −0.06 | −0.08 | 0.10 | 0.024 |
| 3 | 0.11 | 1:112800 | −0.11 | −0.26 | 0.18 | 0.020 | 0.12 | 1:101200 | −0.06 | −0.10 | 0.12 | 0.022 |
| 4 | 0.14 | 1:118700 | −0.26 | −0.92 | 0.96 | 0.025 | 0.24 | 1:66500 | −0.19 | −0.60 | 0.63 | 0.045 |
| 5 | 0.70 | 1:28700 | −0.20 | −0.42 | 0.46 | 0.128 | 0.76 | 1:26600 | −0.33 | −0.51 | 0.60 | 0.139 |
| 6 | 0.58 | 1:4100 | 0.01 | −0.23 | 0.23 | 0.106 | 0.76 | 1:31400 | −0.35 | −0.60 | 0.69 | 0.138 |
2.5 Štatistické testy
Pri hodnotení prístrojov je doporučené používať podľa STN ISO 17 123 štatistické testy [4]. Tieto poskytujú odpovede na štyri otázky, ktoré sú uvedené v tab. 4. Pre tieto testy sa za hladinu významnosti uvažuje hodnota α = 0,05.
| Otázka | Nulová hypotéza | Alternatívna hypotéza |
|---|---|---|
| a) | s ≤ σ | s > σ |
| b) | ~σ = σ | ~σ ≠ σ |
| c) | σx = σy | σx ≠ σy |
| d) | δ = 0 | δ ≠ 0 |
Vypočítaná empirická štandardná odchýlka s je menšia alebo rovná ako jej prislúchajúca hodnota – daná výrobcom?
Patria dve empirické štandardné odchýlky s a ![]() ,určené z dvoch rôznych súborov do rovnakej oblasti predpokladajúc, že obe vzorky majú rovnakú prevažovanú výšku h a rovnaký počet stupňov voľnosti?
,určené z dvoch rôznych súborov do rovnakej oblasti predpokladajúc, že obe vzorky majú rovnakú prevažovanú výšku h a rovnaký počet stupňov voľnosti?
Hodnoty empirických štandardných odchýlok s a ![]() môžu byť získané z:
môžu byť získané z:
dvoch nezávislých súborov meraných údajov, realizovaných tým istým prístrojom ale rôznymi meračmi, dvoch súborov meraných údajov, rovnakým prístrojom, realizovaných v rôznych časových epochách, dvoch súborov meraných údajov, realizovaných rôznymi prístrojmi.
Ak je empirická štandardná odchýlka sx x-ovej zložky, rovná empirickej štandardnej odchýlke sy y-ovej zložky výsledku dosiahnutého prevažovania?
Je odchýlka δ = 0 ? [4].
Otázka a)
Nulová hypotéza H0 sa nezamieta ak je splnené:
kde ![]() .
.
Presnosť udávaná výrobcom pre prístroj Zeiss PZL 100 – σ = 1 : 100 000 = 0,0000100, ak platí nasledujúci vzťah s ≤ 0,0000116, tak sa nulová hypotéza nezamieta. Hodnota s je získaná s pomernej presnosti sISO– plumb podľa vzťahu (16). V tab. 5 sú hodnoty empirických štandardných odchýlok a výsledky štatistických testov pre prístroj č. 1 [3].
| Č. bodu | Prístroj č. 1 : Zeiss PZL 100, v.č. 214 456 | |||
|---|---|---|---|---|
| 1. meranie | 2. meranie | |||
| s | Výsledok štatistického testu | s | Výsledok štatistického testu | |
| 1 | 0.0000121 | H0 sa zamieta | 0.0000164 | H0 sa zamieta |
| 2 | 0.0000089 | H0 sa nezamieta | 0.0000154 | H0 sa nezamieta |
| 3 | 0.0000089 | H0 sa nezamieta | 0.0000099 | H0 sa nezamieta |
| 4 | 0.0000084 | H0 sa nezamieta | 0.0000150 | H0 sa zamieta |
| 5 | 0.0000348 | H0 sa zamieta | 0.0000376 | H0 sa zamieta |
| 6 | 0.0000244 | H0 sa zamieta | 0.0000319 | H0 sa zamieta |
Otázka b)
Nulová hypotéza H0 sa nezamieta ak je splnená nasledujúca podmienka:
Výsledky štatistických testov dvoch nezávislých súborov meraní získané rovnakým prístrojom sú uvedené tab. 6 [3].
| Č. bodu | Prístroj č. 1: Zeiss PZL 100 | Prístroj č. 2: Zeiss PZL 100 | ||||||
|---|---|---|---|---|---|---|---|---|
| s2 | ~s 2 | s2 / ~s 2 | Výsledok štatistického testu | s2 | ~s 2 | s2 / ~s 2 | Výsledok štatistického testu | |
| 1 | 0.00 | 0.00 | 0.51 | H0 sa zamieta | 0.01 | 0.01 | 0.44 | H0 sa zamieta |
| 2 | 0.01 | 0.02 | 0.38 | H0 sa zamieta | 0.01 | 0.01 | 1.00 | H0 sa nezamieta |
| 3 | 0.01 | 0.01 | 0.84 | H0 sa nezamieta | 0.01 | 0.06 | 0.17 | H0 sa zamieta |
| 4 | 0.02 | 0.06 | 0.34 | H0 sa zamieta | 0.03 | 0.03 | 1.00 | H0 sa nezamieta |
| 5 | 0.49 | 0.58 | 0.85 | H0 sa nezamieta | 0.12 | 0.38 | 0.30 | H0 sa zamieta |
| 6 | 0.34 | 0.58 | 0.58 | H0 sa nezamieta | 0.41 | 0.23 | 1.78 | H0 sa zamieta |
Otázka c)
Nulová hypotéza H0 sa nezamieta ak je splnená nasledujúca podmienka [5]:
kde ![]() .
.
Výsledky štatistických testov porovnaním sx x-ovej zložky a sy y-ovej zložky získané rovnakým prístrojom sú uvedené tab. 7 [3].
| Č. bodu | Prístroj č. 1: Zeiss PZL 100, v.č. 214 456 | |||||||
|---|---|---|---|---|---|---|---|---|
| 1. meranie | 2. meranie | |||||||
| sx2 | sy2 | sx2 / sy2 | Výsledok štatistického testu | sx2 | sy2 | sx2 / sy2 | Výsledok štatistického testu | |
| 1 | 0.004 | 0.002 | 1.661 | H0 sa nezamieta | 0.005 | 0.006 | 0.818 | H0 sa nezamieta |
| 2 | 0.006 | 0.005 | 1.310 | H0 sa nezamieta | 0.014 | 0.020 | 0.707 | H0 sa nezamieta |
| 3 | 0.011 | 0.013 | 0.802 | H0 sa nezamieta | 0.014 | 0.015 | 0.944 | H0 sa nezamieta |
| 4 | 0.017 | 0.021 | 0.815 | H0 sa nezamieta | 0.042 | 0.089 | 0.475 | H0 sa nezamieta |
| 5 | 0.342 | 0.645 | 0.531 | H0 sa nezamieta | 0.413 | 0.740 | 0.558 | H0 sa nezamieta |
| 6 | 0.166 | 0.507 | 0.327 | H0 sa zamieta | 0.425 | 0.721 | 0.589 | H0 sa nezamieta |
Otázka d)
Nulová hypotéza H0 sa nezamieta ak je splnená nasledujúca podmienka [5]:
Výsledky štatistických testov otázky d), t.j či odchýlka zámery sa δ nerovná nule je uvedené tab. 2.8 [3].
| Č. bodu | Prístroj č. 1: Zeiss PZL 100, v.č. 214 456 | |||||||
|---|---|---|---|---|---|---|---|---|
| 1. meranie | 2. meranie | |||||||
| δ | ≤ | s ‧ 0,37 | Výsledok štatistického testu | δ | ≤ | s ‧ 0,37 | Výsledok štatistického testu | |
| 1 | 0,05 | > | 0,004 | H0 sa zamieta | 0,04 | > | 0,005 | H0 sa zamieta |
| 2 | 0,09 | > | 0,005 | H0 sa zamieta | 0,10 | > | 0,009 | H0 sa zamieta |
| 3 | 0,31 | > | 0,007 | H0 sa zamieta | 0,12 | > | 0,008 | H0 sa zamieta |
| 4 | 0,96 | > | 0,009 | H0 sa zamieta | 0,63 | > | 0,017 | H0 sa zamieta |
| 5 | 0,46 | > | 0,047 | H0 sa zamieta | 0,60 | > | 0,051 | H0 sa zamieta |
| 6 | 0,23 | > | 0,39 | H0 sa zamieta | 0,69 | > | 0,050 | H0 sa zamieta |
3. Záver
Výsledkom testovania optického prevažovača Zeiss PZL 100 je empirická štandardná odchýlka určenia polohy bodu. Na základe štatistických testov uvedených v tejto časti normy je možné konštatovať či prístroj vyhovuje norme, alebo je potrebná jeho oprava – rektifikácia.
Z testovania vyplýva, že empirická štandardná odchýlka priamo úmerne narastá s prevažovanou výškou, pri väčšom prevýšení je meranie zaťažené aj chybou, ktorá závisí od veľkosti použitej mriežky (rastra). Ak porovnáme vypočítane empirické štandardné odchýlky získané z experimentálnych meraní s hodnotami udávanými výrobcom možno konštatovať, že prístroj vyhovuje norme do prevažovanej výšky 16 m. Odpovede na ostané otázky štatistických testov sú v časti 2.5.
Kontrola, overovanie a testovanie geodetických prístrojov a pomôcok sa stavajú nevyhnutnou súčasťou každej geodetickej práce na stavenisku. Technické normy napriek svojej nezáväznosti stanovujú kritéria a požiadavky kladené aj na túto geodetickú činnosť. Nezáväznosť noriem neznamená ich neplatnosť, ale normy umožňujú efektívne určiť kvalitu a spoľahlivosť používaného prístroja a jeho doplnkov.
Literatura
- [1] Ježko, J.: Testovanie a kalibrácia geodetických prístrojov z pohľadu technických noriem. In.: Interdisciplinárne aplikácie geodézie, inžinierskej geodézie a fotogrametrie. Bratislava, Katedra geodézie SvF STU, 2008, 10 s., (CD ROM) ISBN 978-80-227-2938-3.
- [2] MICHALČÁK, O. a kol.: Inžinierska geodézia II. Alfa – SNTL, Bratislava 1990, s. 357.
- [3]BUJŇÁK, L.: Testovanie geodetických prístrojov podľa STN ISO 17123. Diplomová práca. Katedra geodézie SvF STU Bratislava 2012, 55 s.
- [4] STN ISO 17123-7: 2010 Optika a optické prístroje – Postupy na testovanie geodetických prístrojov. 7. časť: Optické prevažovacie prístroje.
Příspěvek je tematicky zaměřen do oblasti aplikované metrologie a uplatnění standardizovaných postupů kontroly optických provažovačů. Jde o vhodně a srozumitelně komentovaný přepis postupu dle technické normy STN ISO 17123-7: 2010 doprovázený názorným příkladem s obrázky, což je pro stavební i geodetickou praxi užitečné. Testovací postup je aplikovatelný na optické, elektronické a laserové provažovače i centrovače používané ve stavebnictví.
Setting out and control of a vertical direction belong among often solved tasks in civil engineering. In order to setting out a plumb line the optical plumbing instruments are used. The most commonly used instrument for this activity is Zeiss PZL (Zeiss Zenitholt PZL 100). This contribution describes the procedure and results of testing according to STN ISO 17123-7: 2010 Optics and optical instruments – Field procedures for testing geodetic and surveying instruments. Part 7: Optical plumbing instruments.